Magnetically propelled Carreau fluid flow over penetrable sensor surface influenced by thermal radiation, Joule heating and heat generation

B J Gireesha, B Nagaraja, N Srikantha, N G Rudraswamy and A Felicita

1 Department of Studies and Research in Mathematics,Kuvempu University,Shankaraghatta,Shivamogga,Karnataka, India

2 Department of Mathematics, MS Ramaiah Institute of Technology, Bangalore, India

3 Department of Mathematics, P.C.Jabin Science College (Autonomous), Hubballi, India

Abstract This examination emphasizes the analysis of thermal transmission of Carreau fluid flow on a permeable sensor surface equipped with radiation,Joule heating,an internal heat source,and a magnetic field.With the above effects and assumptions,the equations that administer the flow are formulated.A configured system of equations is productively reduced to a system of ordinary differential equations.The reduced system is then dealt with using the Runge-Kutta-Fehlberg fourth-fifth order tool equipped by the shooting technique.Derived numerical solutions are utilized to plot graphs and tables.The conclusion of the study outlines some important findings such as the power law index,the thermal radiation parameter and the heat source parameter enhance the thermal panel whereas the Weissenberg number deescalates the same.The power law index and permeable velocity decrease the velocity panel significantly.Diagrammatic representation of streamlines of the flow has been given to strengthen the study.A detailed description has been produced about the results obtained in the study.

Keywords: sensor surface, Carreau fluid, squeezed flow, thermal radiation, heat generation

Nomenclature

Introduction

A sensor surface holds its significance as one can retrieve its applications in biological and chemical engineering grounds.One such sensitive surface is a micro cantilever which can analyze even a tiny amount of mass.Hence it turns out to be of utmost importance in sensing various compounds simultaneously.It serves a purpose in industrial, military and bioclinical disciplines.An emphasis of the magnetic field on the flow makes the flow problem more relatable to a practical scenario as it avails itself in a nuclear reactor, installation of an electric furnace and many more applications.Electrolytes are the ones that turn out to be magnetohydrodynamic (MHD) fluid.Because of this,there has been an increased interest in studying this effect.Rashidi et al [1] discussed thermodynamic second law within a rotating porous disk.The simulation turns out to be useful in enhancing heat transmission in sustainable energy systems.Hayat et al [2] investigated MHD 3D flow with convective conditions at the boundaries.The solutions are attained by HAM and their results uphold the theory that the Biot number maximizes the transfer of heat.Prasannakumara et al[3]examined Sisko nanofluid flowing over a stretched sheet.The temperature profiles are more influenced by non-linear radiation than that of linear.Lund et al [4] laid their effect in analyzing dual solutions for Williamson fluid flowing with slippage; the presence of the buoyancy force has contributed to finding dual solutions.Tassaddiq et al[5]investigated Casson fluid flow with Newtonian heating by making use of the fractional model along Mittag-Leffler memory.Kumar et al [6], by considering the vertical plate that is impulsively initiated, studied the impact of thermal radiation and declared that velocity and temperature escalate by maximizing the radiation supply.

The fluids responsible for practical implications do not manifest the property of the Newtonian fluid; hence there was origination of the concept of the fluid that is not Newtonian.Carreau fluid is one such fluid.Ellahi et al[7]emphasized such fluid flow in a rectangle shaped duct.Akbar and Nadeem [8]created a model for flow of the blood utilizing Carreau fluid with stenosis that is axially not symmetric but symmetric radially whereas Khan et al [9] outlined a numerical study of the same fluid by squeezing the plate over the sensor surface by varying thermal conductivity.Kumar et al[10]investigated the radiative transport of heat by suspending fluid particles within the Carreau fluid.Ali et al [11] incorporated the designed microbes in the flow and studied the interactions between them and Carreau fluid biologically with magnetic effects.The Taylor swimming sheet model is used to serve this purpose.The Homann chemically active stagnation point Carreau fluid flow was examined by Khan et al[12].The implementation of Fick’s and Fourier law in their modified form makes the flow study more interesting.Heat transport impacts on electro-MHD Carreau fluid allowed amid micro but parallel plates were scrutinized by Bhatti et al [13].

Sensors are involved in most computing devices.A micro cantilever is the sensing element used in the functioning as it has the capacity to diagnose many sicknesses.Their high sensitivity property and low cost aids their use in sophisticated applications.To this end, many of researchers have shown their concern in contributing to this field.Dijkstra et al[14]gave their insights on the thermal flow sensor in miniaturized devices with integratedplanar sensor arrangement on semicircular microchannels suspended by silicon-nitride.Akgül and Pakdemirli [15] analyzed Lie group theory for fluid that is not Newtonian,allowed over a pervious surface.Haq et al [16] utilized functionalized metalnano-sized particles over this surface and studied the squeezed flow.In their research they discussed thatCu-nano-sized particles promote a better transport of heat.A compressed flow of a time-reliant tangent hyperbolic fluid on the sensor surface was investigated by Kumar et al [17].Hussain et al [18] analyzed magneto-pseudoplastic fluid flowing across a sensor surface.An assimilation of the energy equation in their model is obtained by Fourier’s law.Waini et al [19] explored hybrid nano-liquid squeezed flow over a sensor surface.Their results elucidate that the rate at which the heat is transferred is higher for a hybrid fluid than for a regular fluid.

Daniel and Daniel [20] explored buoyancy, the radiation effect on MHD flow using HAM.It is noted that the hydrodynamic and thermal boundary layer escalates with excessive exposure to radiation.Sheikholeslami and Rokni [21]numerically simulated the consequence of Coulomb force on heat transport of a nanofluid in a thermally radiated porous enclosure.They deduced that nano-sized particles that have a platelet shape have a high Nusselt number.Gireesha et al[22]made use of the Cattaneo-Christov model to study dusty Casson fluid with melting heat transport.Comparison of their work with previous one highlights the precision of their method.Muhammad et al [23] revealed the implication of radiation in the Powell-Eyring 3D nanomaterial flow.To understand the transport of heat and mass flux,non-Fourier’s,non-Fick’s hypothesis is applied.

Hayat and Qasim[24]together attained the results for Joule heating influence on Maxwell fluid involving the thermophoresis effect.Sánchez et al [25] analyzed non-Newtonian fluid flow along a slit microchannel; Joule heating modifies the fluid features,which in turn alters the electric potential and further on the flow field.Babu and Narayana[26]elucidated the MHD mixed convective influence on a Jeffrey fluid with power law heat flux.The Deborah number has major influence on thermal and momentum boundary layer.Qayyum et al[27]investigated the comparison of five nano-sized particles in a spinning disk provided with slip.Their study revealed that for a higher volume fraction of particles,the velocity along the axis decays and as the thermal conductivity ofAg-H2Ois more, the temperature is also high.Nazeer et al[28]analytically described the radiative,Joule heating impact on electro-osmotic liquid flow.

Sheikh et al [29] compared two different fractional derivatives for Casson fluid flowing with heat production.The velocity profile attained from these methods at unit time is noted to be identical whereas the deviations grow higher with the time greater than unity.Khan and Sardar [30] explored heat generated as well as absorbed in 3D Carreau fluid flow.They carried out the analysis by keeping the shear rate infinite.Tlili [31] independently worked on microgravity environment by allowing Jeffrey fluid to flow upon a sheet being stretched.Hafeez and Khan [32] looked into Cattaneo-Christov theory in a spinning disk.The disk undergoes rotation as well as stretching and the influence of heat production is also noted.Further investigations have been carried out by many authors [33-35] in their field of study.

A sensor surface is a geometrical means over which the magnetized Carreau fluid is allowed to flow.A squeezed 2D flow is reliant on time.A sensor surface is exposed to radiation and its impact is scrutinized.Thermal performance of the flow is explored under persuasion of an internal heat source and Joule heating.All these effects are pronounced to form an irresistible flow demeanor.Manifestation of the graphs is crucial in checking the consequence of the flow.Drag force and the Nusselt number are computed together with velocity and thermal profiles.The streamlines are drawn in order to understand the outline of the flow.

Mathematical illustration

Consider a 2D, time-reliant, squeezed Carreau fluid flow driven by a penetrable sensor surface.The heighth(t) of the closed compressed channel is considered much higher than the thickness of the boundary layer as in figure 1.Furthermore, the magnetic fieldB0is operated at a normal channel direction.The upper plate is squeezed whereas the lower plate is left to be immovable.Joule heating, radiation and internal heat source impacts are also considered to observe the thermal performance of the flow.

Figure 1.Schematic representation of the flow model.

The mathematical representations of continuity,momentum and heat are shown as [9]:

Here,u,v-velocity attributes respectively alongxandydirections,Uis the free stream velocity,nis the power law index,νis the kinematic viscosity,Γ is the time constant,pis the pressure,αis the thermal diffusivity,Trepresents temperature,trepresents time,ρrepresents density,σrepresents electric conductivity,Cprepresents specific heat capacity,qrrepresents radiative heat flux,Q0represents internal heat source,T∞represents temperature far from the surface.Further, on removing a pressure attribute from (2) and (3), it takes the form,

with tangled peripheral conditions:

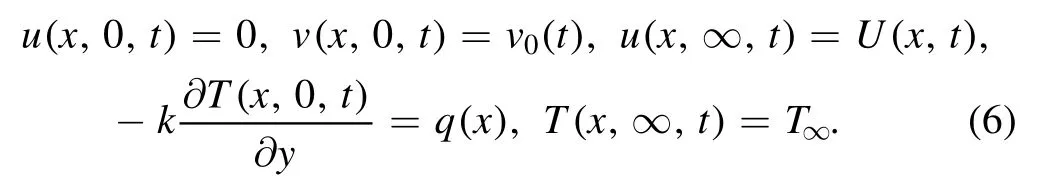
According to Taylor series expansionT4is expressed as

On deducting terms of order above first degree, we get

Employing (9) in equation (7), we get

The below mentioned similarity elements are applied to transform equations (4) and (5).

Here,bis the index of the squeezed flow,sis an arbitrary constant,ais the strength of squeezed flow,ψis the stream function,q0is the reference heat flux.The height of the channel movements is described by the condition:h(t)=andwhereh0is a constant.Clearly, equation (1) is sufficiently satisfied and the remaining equations are transformed as follows:and the associated boundary conditions are transfused into

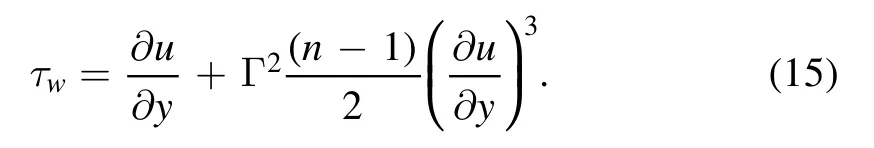
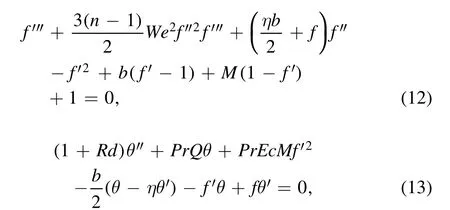
The elements of drag and the Nusselt number are deduced as

The transformed expression for equation(16)is given by,

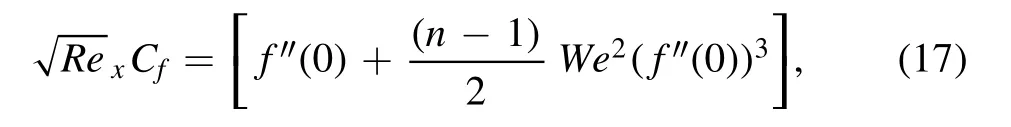
Results and discussion

Present scrutiny emphasizes to analyze the thermal transmission and flow of Carreau fluid, upon permeable sensor surface equipped with radiation, Joule heating, internal heat source and applied magnetic field.The numerical solutions are obtained for all flow profiles by varying different parameters.The graphs are plotted using numerical extractions and a detailed discussion has been given subsequently.

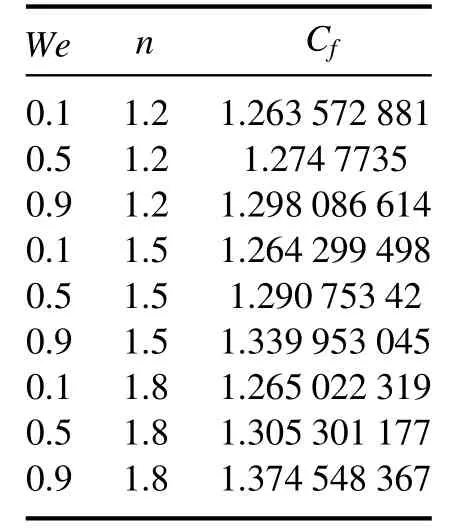
Table 1.Variation of skin friction coefficient for various values of We and n.

Power law index behaviornon velocity is demonstrated in figure 2.As power law index(n) is closely related to friction factor, it is obvious from figure 2 that with a rise in the power law index there is reduction in velocity at the boundary region.On risingnthe fluid exhibits the shear thickening property thus diminishing the velocity.This ascertains that magnification inncauses a reduction in the field which avoids the fluid motion.But an increase in the thermal boundary layer thickness is noted, resulting in boosting the fluid’s temperature in the boundary (figure 3).

Figure 2.Repercussion of power law index( n) on the velocity regime( f′( η)).

Figure 3.Repercussion of power law index( n) on thermal regime( θ ( η)) .

Figures 4 and 5 depict the variation of permeable velocity(f0)on velocity and temperature.A drop in velocity and augmentation in temperature is noticed for suction case.A decrease in velocity is observed due to the increase in temperature results in decrease in wave velocity owing to suction.

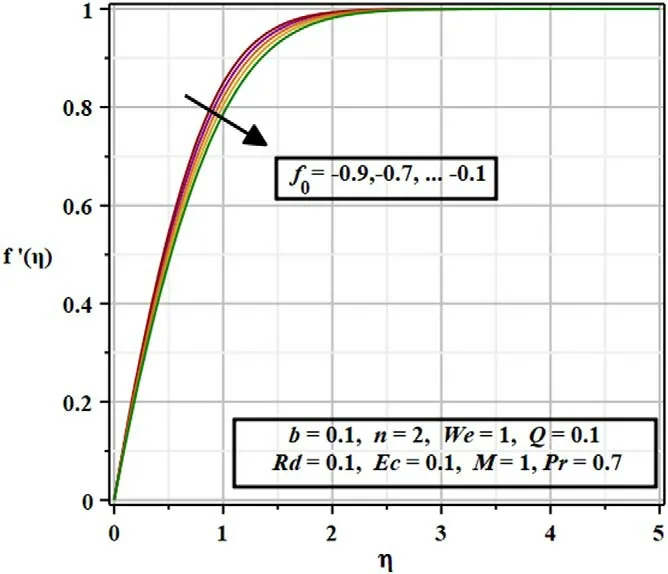
Figure 4.Repercussion of permeable velocityon the velocity regime( f′( η)).

Figure 5.Repercussion of permeable velocity on thermal regime( θ ( η )).

Figures 6 and 7 depict the conduct of the squeezed flow index(b) onf′(η)andθ(η) .Clearly an increment inbcauses depletion in velocity and temperature.Figures 8 and 9 show that fluid velocity swells over a sensor surface which is admitted with the substantial increase in temperature in the boundary as a result of the increase in thermal diffusivity.

Figure 6.Repercussion of squeezed flow parameter( b) on the velocity regime( f′( η)).

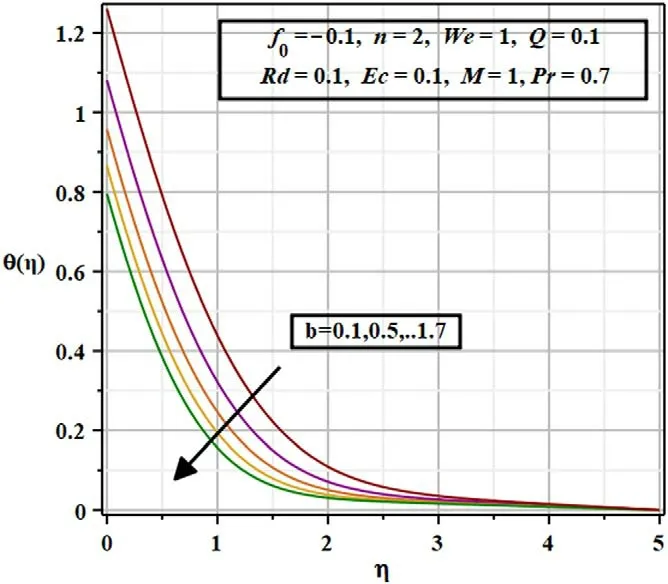
Figure 7.Repercussion of squeezed flow parameter( b) on the thermal regime( θ ( η)) .

Figure 8.Repercussion of Magnetic parameter( M) on the velocity regime( f′( η)).

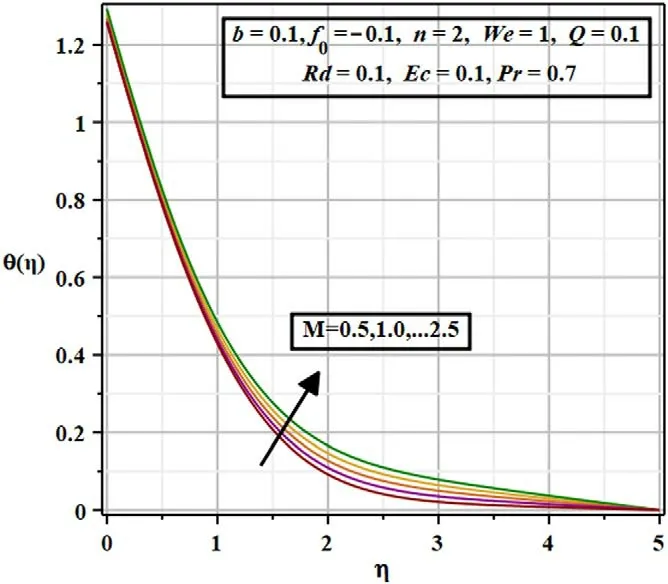
Figure 9.Repercussion of magnetic parameter( M) on the thermal regime( θ ( η)) .

Figures 10 and 11 reflect the Weissenberg number(We)impact on velocity,temperature profiles.Weshows a negative impact on the flow regime forn＞ 1 causing a substantial rise in temperature of the fluid at the boundary.This nature of theWeis solely characterized byn, On magnification ofn, fluid exhibits shear-thickening trait which shows the declination of velocity with a rise inWe.

Figure 10.Repercussion of Weissenberg number( We) on the velocity regime( f′( η)).

Figure 11.Repercussion of the Weissenberg number( We) on the thermal regime( θ ( η)) .

RdandQshow similar behavior in the thermal boundary layer(figures 12 and 13 respectively),but the effect ofQhas a greater impact in the boundary causing an exponential enhancement in the fluid’s temperature for fixedRd.When we riseQthere is enrichment of heat production in the interior of the channel.As a consequence, thermal energy enhances and there is a rise in temperature.

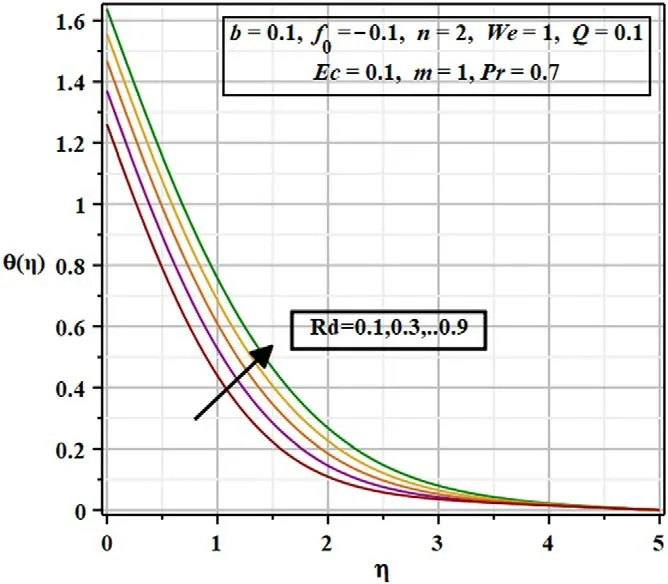
Figure 12.Repercussion of the radiation parameter( Rd) on the thermal regime( θ ( η)) .

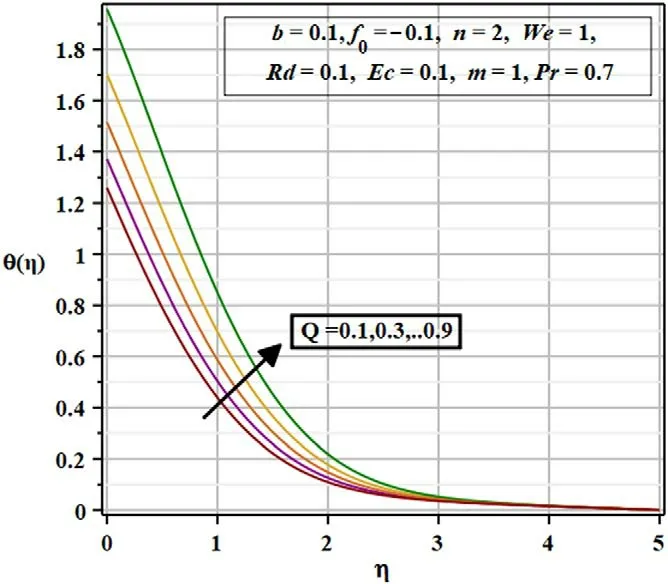
Figure 13.Repercussion of the heat source parameter( Q) on the thermal regime( θ ( η)) .

Figures 17-19 show the streamlines of the stated flow.Three different sets of streamlines for various ranges ofMas such0.2, 1.2, 2 are drawn to illustrate the flow characteristics which shows that an increase inMdrags the streamlines towards thex-axis.The rationale for the stretching of streamlines towards thex-axis is the increased presence of the applied magnetic field.Table 1 shows the variation of skin friction coefficient for different values ofWeandn.

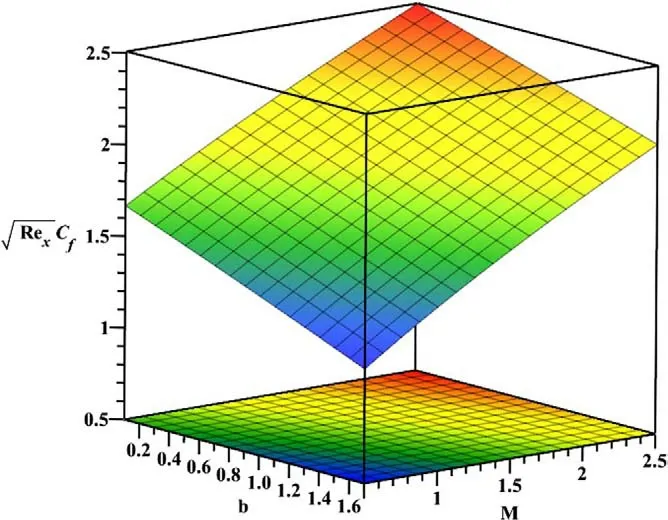
Figure 14.Repercussion of squeezed flow parameter( b) on the coefficient of skin friction against the magnetic parameter( M) .

Figure 15.Repercussion of Weissenberg number( We) on the coefficient of skin friction against the squeezed flow parameter( b) .

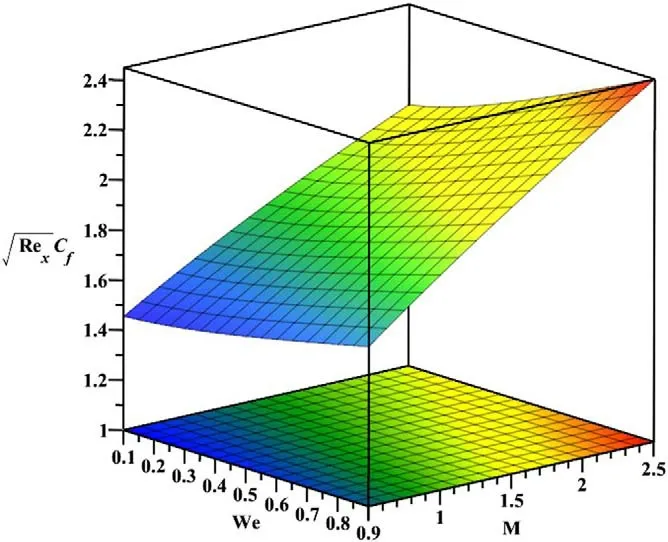
Figure 16.Repercussion of Weissenberg number( We) on coefficient of skin friction against the Magnetic parameter( M) .

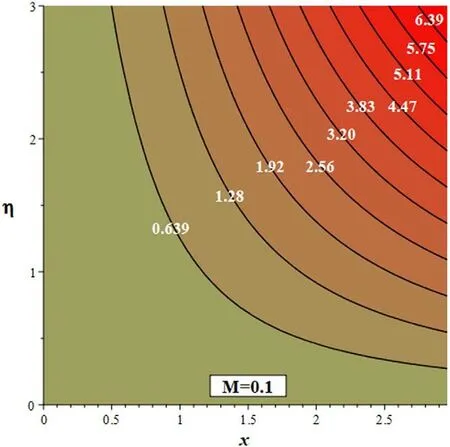
Figure 17.Streamlines of the flow whenM= 0.1.

Figure 18.Streamlines of the flow whenM= 1.2.

Figure 19.Streamlines of the flow whenM= 2.

Conclusion

This work focused on analyzing the Carreau fluid allowed to flow above a sensor surface when the flow is affected by a magnetic field and liable to radiation.The results are obtained by an effective numerical method and the plots are explained.A summary of them is given as follows:

· Velocity is recorded as declining by enhancingn,f0,b,Weand velocity is amplified by risingM.

· It is noted that the parameters liken,f0,M,We,RdandQmaximize temperature whereas it is minimized byb.

· On escalatingbon the flow the drag force is magnified when compared to the magnetic parameter.

· For a different range ofWethe drag force is augmented when examined againstb.

· Streamlines for the flow on various strengths ofMenlightens the fluid particles path.

· The benefit of flow driven by a penetrable sensor surface finds its applications in numerous grounds including biomedical, chemical sensing and engineering.

Acknowledgments

The authors are thankful to the Department of Science and Technology,Government of India under DST-FIST Program(Ref No.SR/FST/MS-I/2018-2023) for supporting the Department of Mathematics, Kuvempu University, Shankaraghatta.

Declaration of conflict of interest

All the authors acknowledge that there is no conflict interest to this article.