The Sharma-Tasso-Olver-Burgers equation: its conservation laws and kink solitons

K Hosseini, A Akbulut, D Baleanu and S Salahshour

1Department of Mathematics, Near East University TRNC, Mersin 10, Turkey

2 Department of Mathematics-Computer, Art-Science Faculty, Eskisehir Osmangazi University, Eskisehir,Turkey

3 Department of Mathematics, Faculty of Arts and Sciences, Cankaya University, Ankara 06530, Turkey

4 Institute of Space Sciences, Magurele-Bucharest, Romania

5 Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey

Abstract The present paper deals with the Sharma-Tasso-Olver-Burgers equation (STOBE) and its conservation laws and kink solitons.More precisely,the formal Lagrangian,Lie symmetries,and adjoint equations of the STOBE are firstly constructed to retrieve its conservation laws.Kink solitons of the STOBE are then extracted through adopting a series of newly well-designed approaches such as Kudryashov and exponential methods.Diverse graphs in 2 and 3D postures are formally portrayed to reveal the dynamical features of kink solitons.According to the authors’ knowledge, the outcomes of the current investigation are new and have been listed for the first time.

Keywords: Sharma-Tasso-Olver-Burgers equation, conservation laws, Kudryashov and exponential methods, kink solitons, dynamical features

1.Introduction

Partial differential equations (PDEs) particularly their nonlinear regimes are applied to model a wide variety of phenomena in the extensive areas of science and engineering.As useful tools for simulating many nonlinear phenomena, such models play a pivotal role in progressing the real world.During the past few decades,one of the major goals has been the construction of novel approaches to extract solitons for PDEs.In the last years, several well-organized methods have been proposed to derive solitons of PDEs, the hyperbolic function method [1-4], the modified Jacobi methods [5-8],the Kudryashov method [9-14], and the exponential method[15-20], are samples to point out.

It is noteworthy that all conservation laws of PDEs do not include physical meanings, however, such laws are essential to explore the integrability and reduction of PDEs [21, 22].Conservation laws of PDEs can be found by using a wide range of methods such as the multiplier approach,the Noether approach,the new conservation theorem, and so on.Of these, the new conservation theorem was first established by Ibragimov and is associated with the formal Lagrangian, Lie symmetries, and adjoint equations of PDEs.Conservation laws can be derived for every symmetry of PDEs and the obtained conservation laws are referred to as trivial or non-trivial [23-29].

In the present study, the authors deal with the following Sharma-Tasso-Olver-Burgers equation [30]

and derive its conservation laws and kink solitons.As is clear from the name of equation (1), such a model consists of the Sharma-Tasso-Olver and Burgers equations.These equations have been the main concern of a lot of research works.Or-Roshid and Rashidi [31] employed an exponential method to derive the solitons of these equations.In another investigation,multiple solitons of these equations were obtained by Wazwaz in[32]through the simplified Hirota’s method.Very recently, Hu et al [33] constructed soliton, lump, and interaction solutions of a 2D-STOBE using a series of systematic ansatzes.

Kudryashov and exponential methods, as privileged approaches, have been applied by many scholars to retrieve solitons of PDEs.Particularly, the effectiveness of these methods has been demonstrated by Hosseini et al in several papers.Hosseini et al [34] derived solitons of the cubicquartic nonlinear Schrödinger equation using the Kudryashov method.The exponential method was utilized in [35] by Hosseini et al to acquire solitons of the unstable nonlinear Schrödinger equation.

The rest of the current study is as follows: In section 2,the conservation theorem and the foundation of Kudryashov and exponential methods are given.In section 3, the formal Lagrangian, Lie symmetries, and adjoint equations of the STOBE are established to derive its conservation laws.In section 4, Kudryashov and exponential methods are adopted to seek solitons of the STOBE.Section 4 further gives diverse graphs in 2 and 3D postures to demonstrate the dynamical features of kink solitons.The achievements of the present paper are provided in section 5.

2.The conservation theorem and methods

In the current section, the conservation theorem and the foundation of Kudryashov and exponential methods are formally given.

2.1.The conservation theorem

To start, suppose that a PDE can be expressed as

wherePis a polynomial.The Lie point symmetry generator of equation (2) is given by

whereξx(x,t,u),ξt(x,t,u),andη(x,t,u)are known as the infinitesimals.The kth prolongation of equation (3) is retrieved by

where

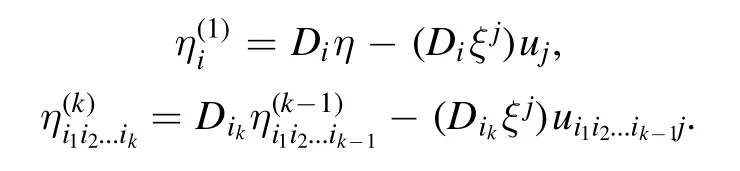
Abovei,j=1, 2andil= 1forl=1, 2,...,k.The total derivative operator is indicated byDi.

The formal Lagrangian is given by multiplying equation (2) bywas follows

L=wP,

wherewis the adjoint variable.It is noteworthy that the adjoint equation is retrieved by

If the solution of equation (4) is found, then, a finite number of conservation laws for equation (2) are derived.

Theorem 1.Every Lie point, Lie-Bäcklund, and nonlocal symmetry of equation (2) results in a conservation law.The components of the conserved vector are given by [29]

whereW=η-ξj uj,andξiandηare the infinitesimal functions.The conserved vectors generated by equation (5)consist of the arbitrary solutions of the adjoint equation.Consequently, one derives a finite number of conservation laws for equation (2) byw[36].

Theorem 2.Derived conserved vectors using (5) are conservation laws of equation (2) if

Di(Ti)=0.

Here,Diis referred to as the total derivative [37].

2.2.Foundation of methods

The Kudryashov method applies the following series [9, 10]

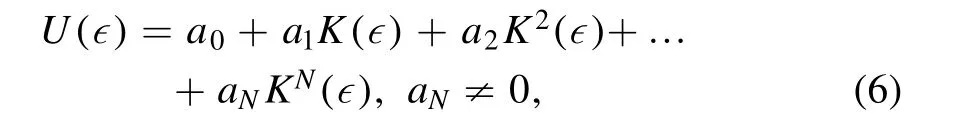
as the nontrivial solution of

Above,a i,i= 0, 1,...,Nare unknowns,Nis retrieved by the balance approach, and

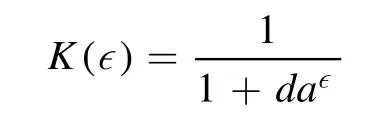
is the solution of

Equations (6) and (7) together result in a nonlinear system which by solving it, solitons of equation (7) are derived.

The exponential method investigates a solution for equation (7) as [15, 16]

where the unknowns are acquired later andN∈ ℤ+.

Again, equations (7) and (8) together yield a nonlinear system which by solving it, solitons of equation (7) are obtained.

3.The STOBE and its conservation laws

In the present section, the conservation theorem is applied to the STOBE to derive its conservation laws.First, the formal Lagrangian is derived in the following form

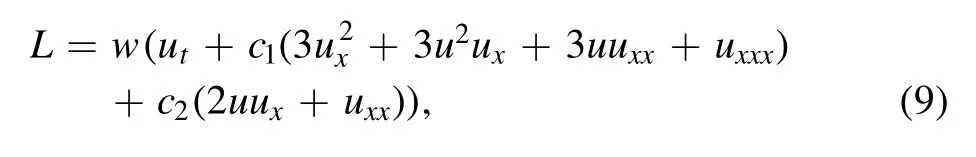
wherewis the adjoint variable.

The adjoint equation is acquired with the aid of the variational derivative as

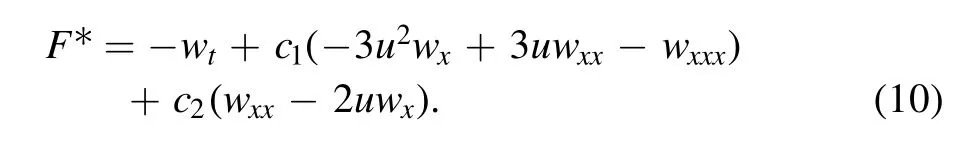
Ifuis replaced bywin equation(10),then,equation(1)is not obtained.Thus,equation(1)is not self-adjoint.In such a case,one can say thatw=1 is a solution of equation (10).

A one-parameter Lie group for equation (1) is given by

whereεis the group parameter,and consequently equation(1)admits following Lie point symmetry generator

Obviously,Xmust be satisfied the Lie symmetry condition as follow

The third prolongation of the Lie point symmetry generator is given by

where

If we applyX(3)to equation (1), an equivalent condition is obtained as

Table 1.The commutator table for the above symmetries.

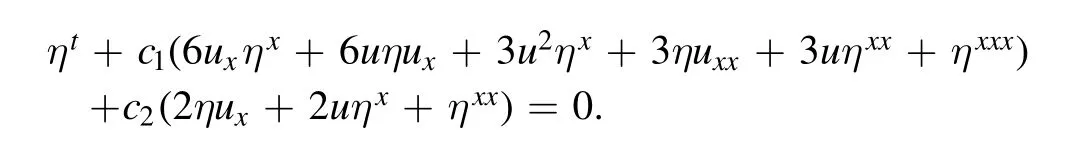
Now, after some operations, we find the infinitesimal functions as follows

wherek1,k2,andk3are arbitrary constants.Finally, the Lie point symmetry generators of equation (1) are given by

The commutator table for the above symmetries (see equation (11)) has been given in table 1.

Now, conservation laws of the STOBE for all founded Lie point symmetry generators are derived.Conservation laws formulae for equation (1) are as follows

Case 1.If we employ (12) and (13) to equation (9) with the use ofX,1we acquire the following conservation laws

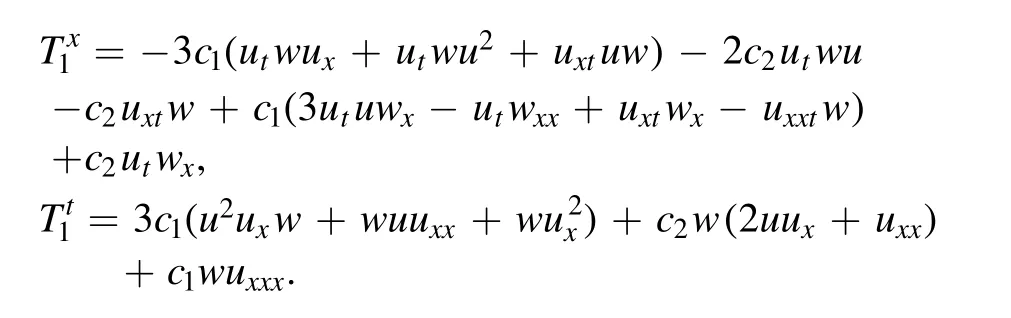
Due to the satisfaction of the divergence condition,these conservation laws are called local conservation laws.Such conservation laws are infinite trivial conservation laws.In this case, we have

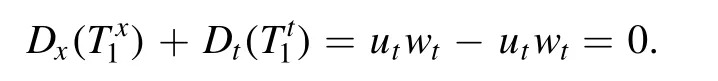
It is noted that forw=1, fromandone can find

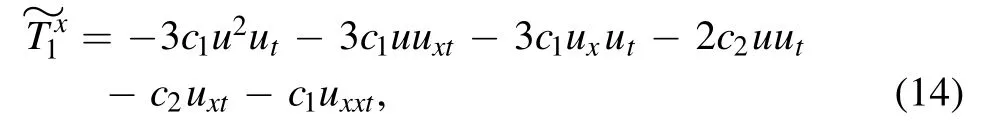
Finite conserved vectors (14) and (15) satisfy the divergence condition, so they are trivial conservation laws.

Case 2.If we apply(12)and(13)to equation(9)with the aid ofX2,we find the following local conservation laws

Owing to the satisfaction of the divergence condition, these conservation laws are called local conservation laws.Such conservation laws are infinite trivial conservation laws.In this case, we have

It is notable that forw=1, one can get

The above finite conserved vectors satisfy the divergence condition, consequently, they are trivial conservation laws.

Case 3.If we employ (12) and (13) to equation (9) with the use ofX3,we obtain the following conservation laws

Due to the satisfaction of the divergence condition, these conservation laws are called local conservation laws.Such conservation laws are infinite trivial conservation laws.

It is noted that forw=1, one can find

Such conserved vectors satisfy the divergence condition, so,they are trivial conservation laws.

4.The STOBE and its solitons

In the present section, Kudryashov and exponential methods are adopted to seek solitons of the STOBE.The present section further gives diverse graphs in 2 and 3D postures to demonstrate the dynamical features of kink solitons.To start,we establish a transformation as follows

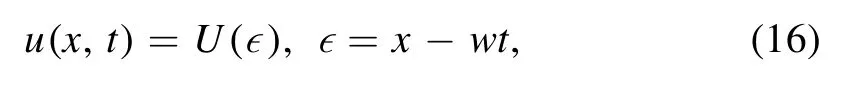
whichwis the soliton velocity.Equations (16) and (1)together result in

4.1.Kudryashov method

Equation (6) andN=1 offer taking the following solution

for equation(17).From equations(17)and(18),we will attain a nonlinear system as

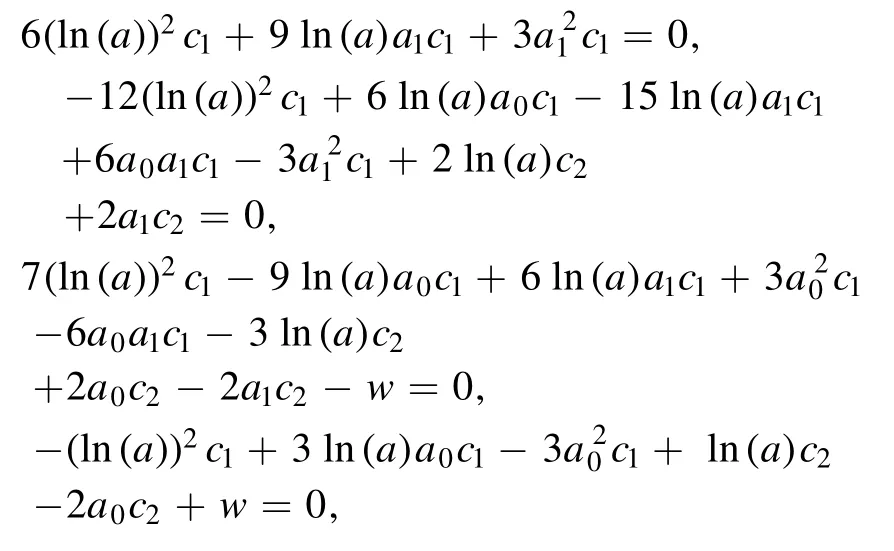
where its solution yields

Case 1:

Thus, the following soliton to the STOBE is acquired

Case 2:

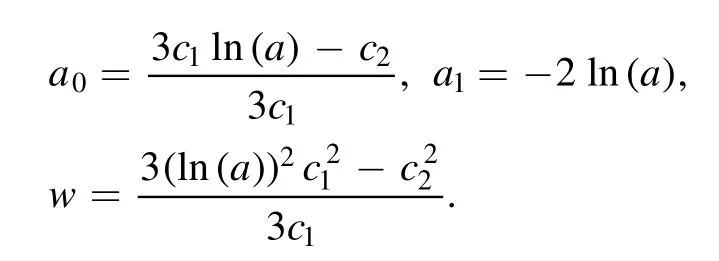
Thus, the following soliton to the STOBE is derived

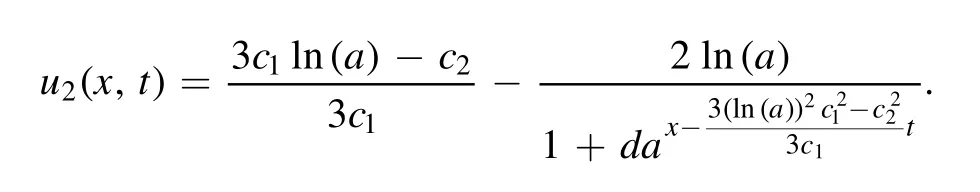
The dynamical features of the kink solitonu2(x,t)are given in figure 1 forc1= 0.15,c2= 0.15,d= 5,anda=2.7.

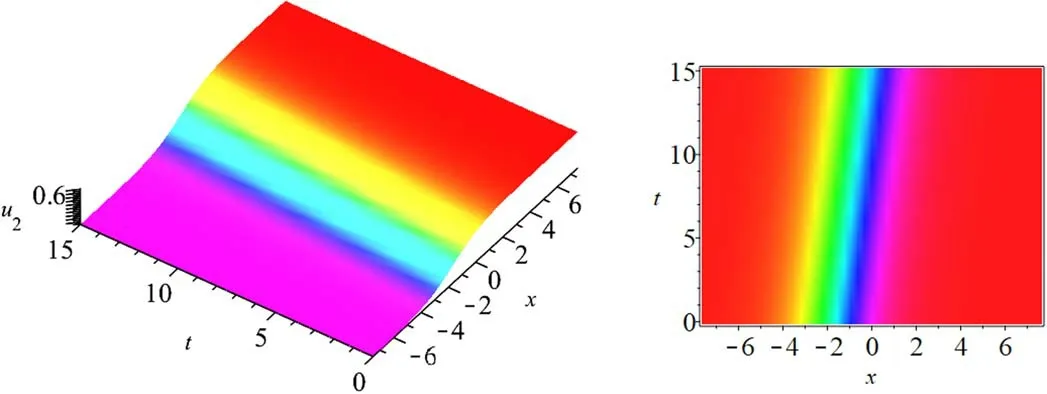
Figure 1.The kink soliton u2 ( x ,t)forc1 = 0.15,c2 = 0.15,d = 5,and a =2.7.

4.2.Exponential method

TakingN=1 in equation (8) leads to

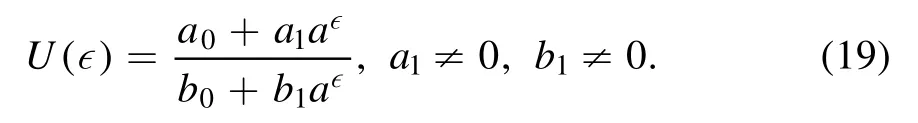
From equations (17) and (19), we will achieve a nonlinear system as

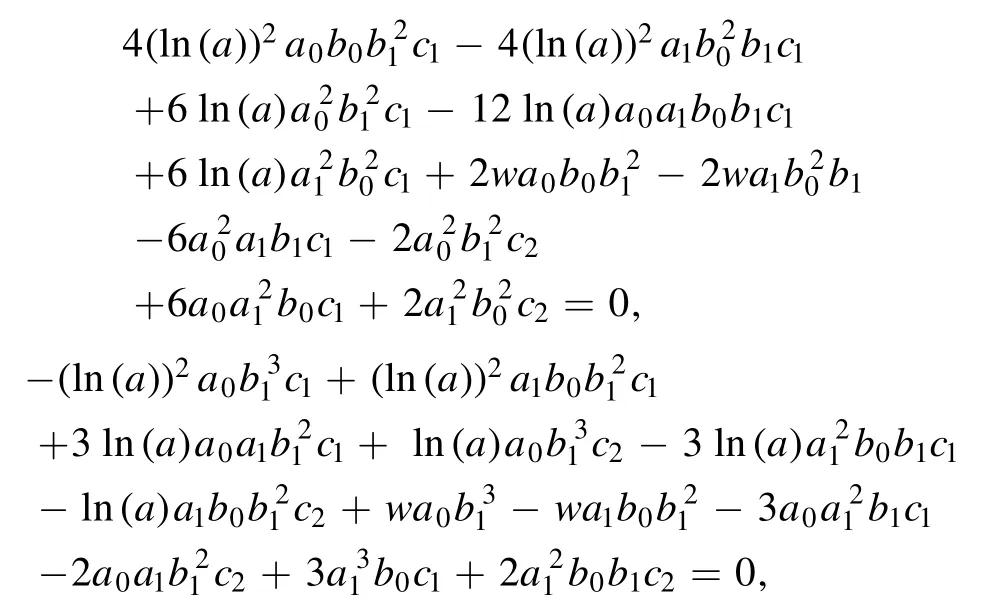
where its solution results in

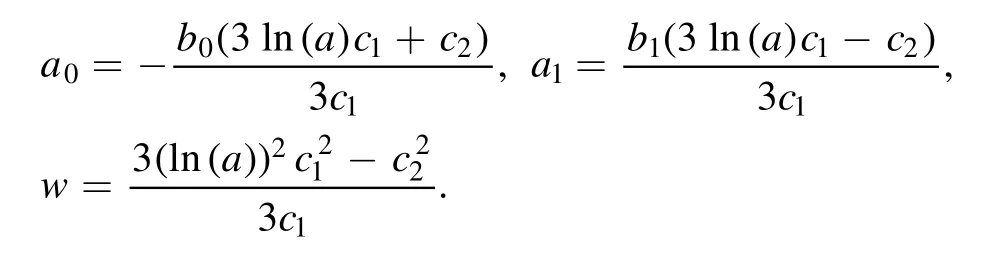
Thus, the following soliton to the STOBE is acquired

where

TakingN=2 in equation (8) yields

Equations (17) and (20) together result in a nonlinear system whose solution gives

Case 1:

Thus, the following soliton to the STOBE is derived

where

Case 2:

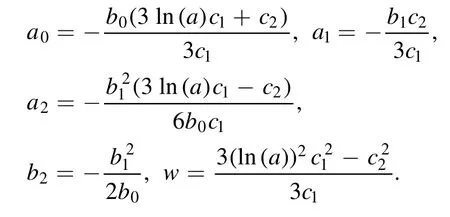
Consequently, the following exact solution to the STOBE is obtained

where

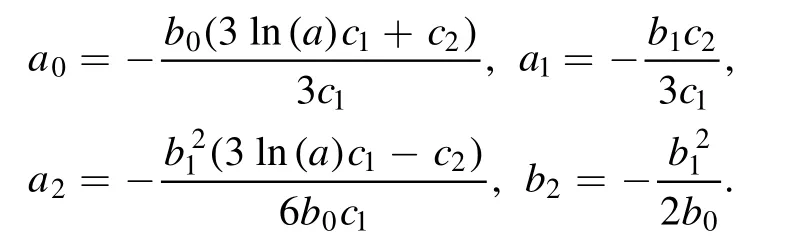
Figure 2 gives the dynamical features of the kink solitonu2(x,t)fora1= -1 ,b0= 1,b2= 1,c1= 0.15,c2=0.15,anda=2.7.Furthermore,the physical behaviors ofu2KMandu2EMfor above parameters have been given in figure 3 whent=0.

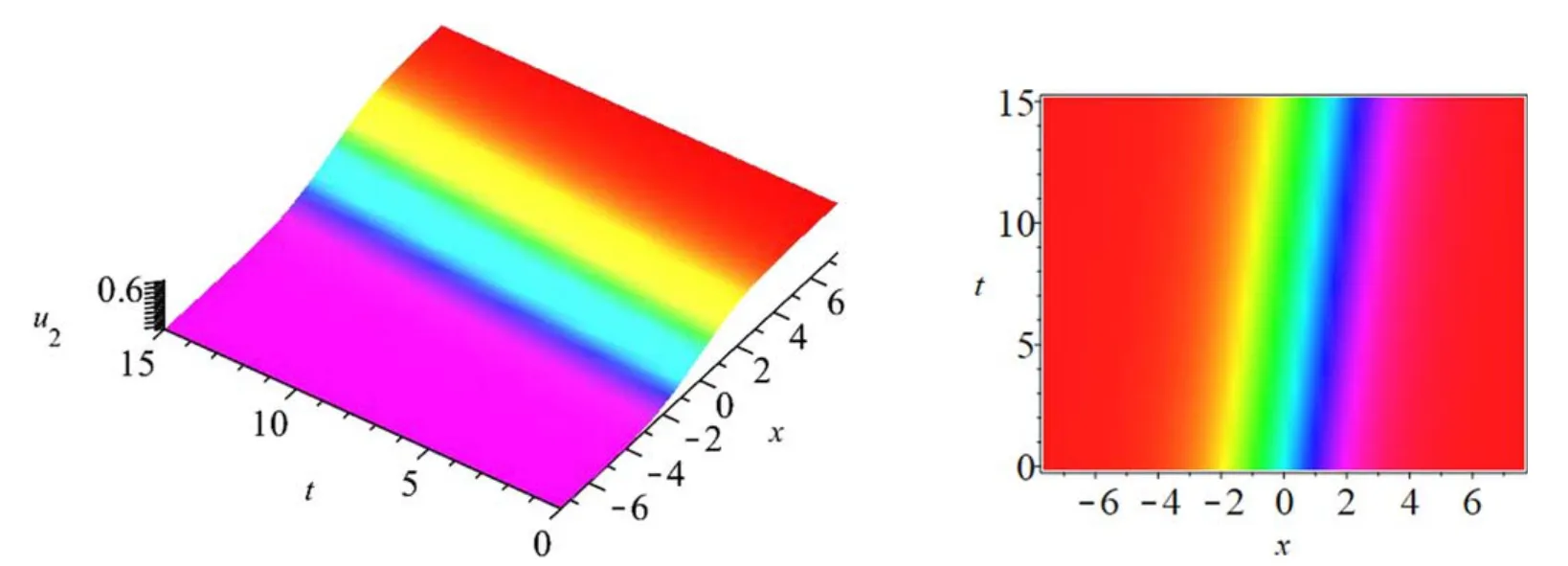
Figure 2.The kink soliton u 2 ( x ,t)for a1 = - 1,b 0 = 1,b 2 = 1,c1 = 0.15,c2 = 0.15,and a =2.7.

Figure 3.u2KM and u2EM for above parameters whent =0.

Remark 1.According to the authors’ knowledge, the outcomes of the current investigation are new and have been listed for the first time.

Remark 2.The authors successfully used a symbolic computation system to check the correctness of the outcomes of the current paper.

5.Conclusion

The principal aim of the current paper was to explore a newly well-established model known as the Sharma-Tasso-Olver-Burgers equation and derive its conservation laws and kink solitons.The study proceeded systematically by constructing the formal Lagrangian,Lie symmetries,and adjoint equations of STOBE to acquire its conservation laws.Besides, kink solitons of the STOBE were formally established using Kudryashov and exponential methods.Various plots in 2 and 3D postures were graphically represented to observe the dynamical characteristics of kink solitons.Based on information from the authors, the outcomes of the current investigation are new and have been listed for the first time.The authors’suggestion for future works is employing newly well-organized methods [38-44] to acquire other wave structures of STOBE.

Declaration of competing interest

The authors declare no conflict of interest.

ORCID iDs