结合流形学习与逻辑回归的多标签特征选择
2022-03-12马盈仓朱恒东
张 要,马盈仓,朱恒东,李 恒,陈 程
(西安工程大学 理学院,西安 710600)
0 概述
特征选择作为处理高维数据分类的主要方法,在算法学习过程中不仅能够减少训练时间,而且能避免维度灾难与过拟合等问题[1-3],同时是近年来机器学习领域的研究热点之一。与单标签数据一样,多标签数据存在多个特征[4],在分类问题中同样面临维度灾难问题,但与传统单标签特征选择不同,多标签特征选择不仅要考虑样本与标签间的关系,而且要考虑标签与标签间的关系。现有多标签特征选择方法大致可分为过滤式、封装式、嵌入式[5]等3 类,其中嵌入式方法是将特征选择过程嵌入学习过程中,综合了过滤式与封装式的优势。
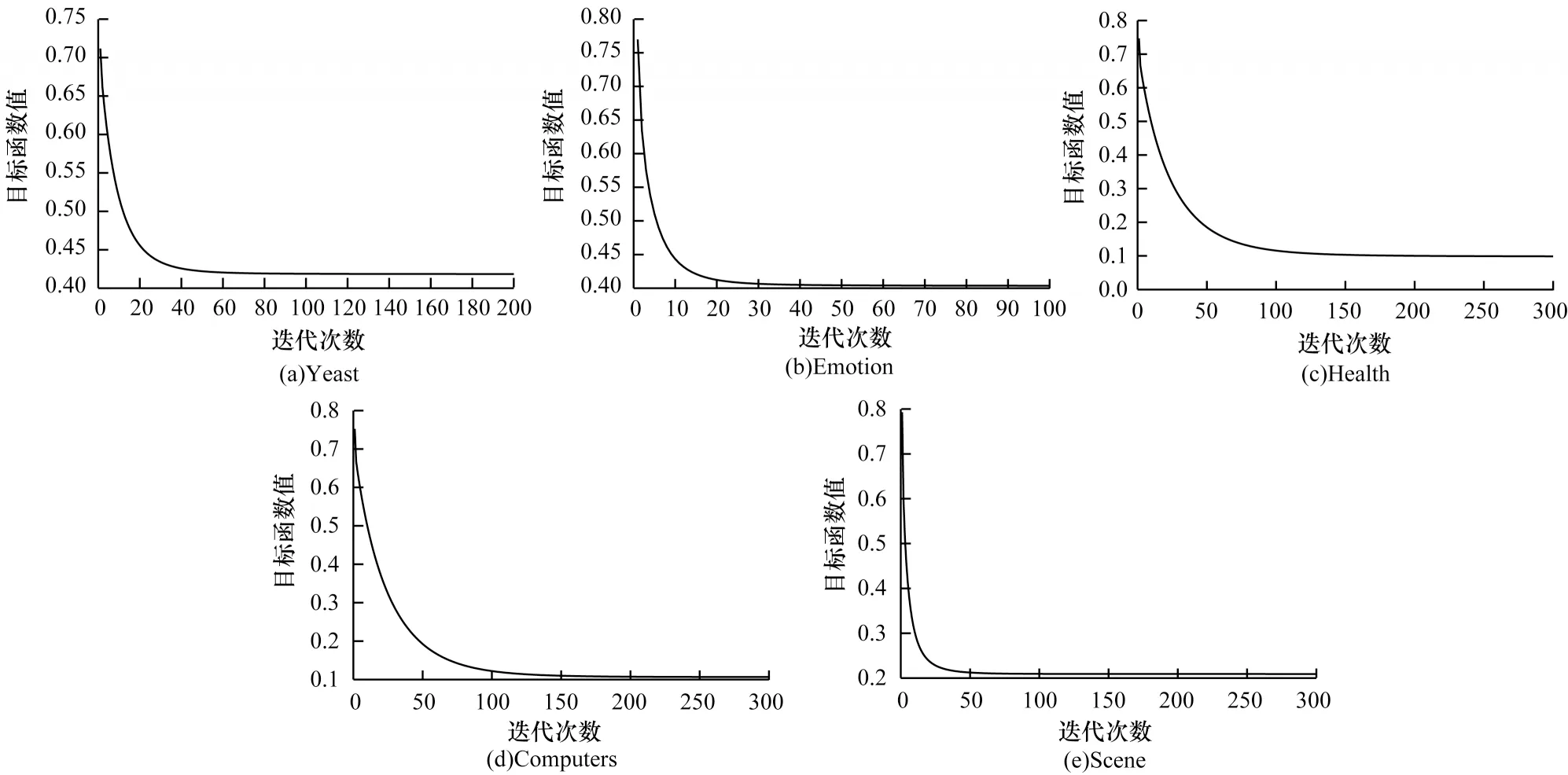
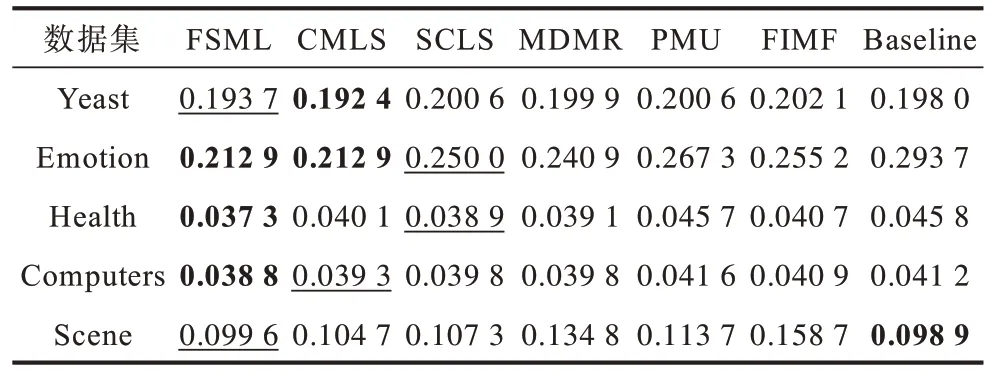
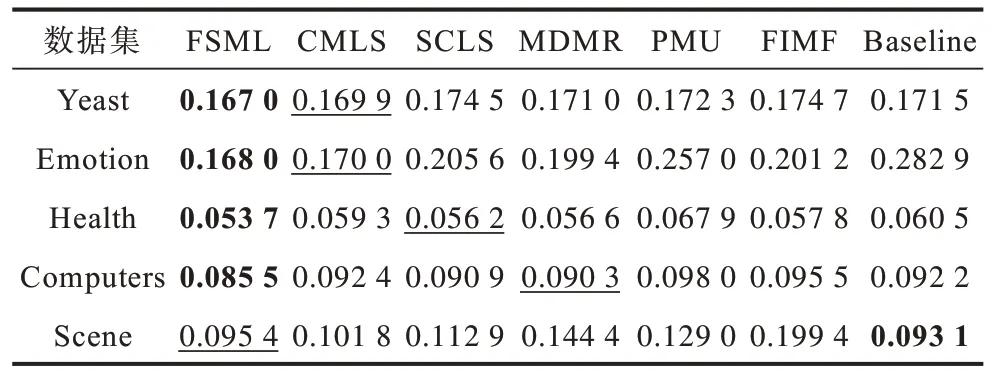
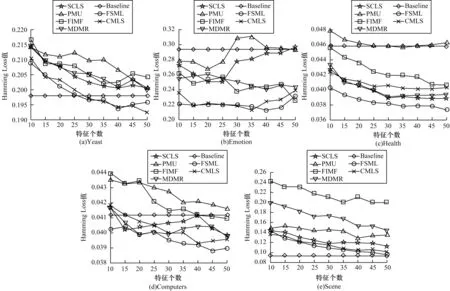
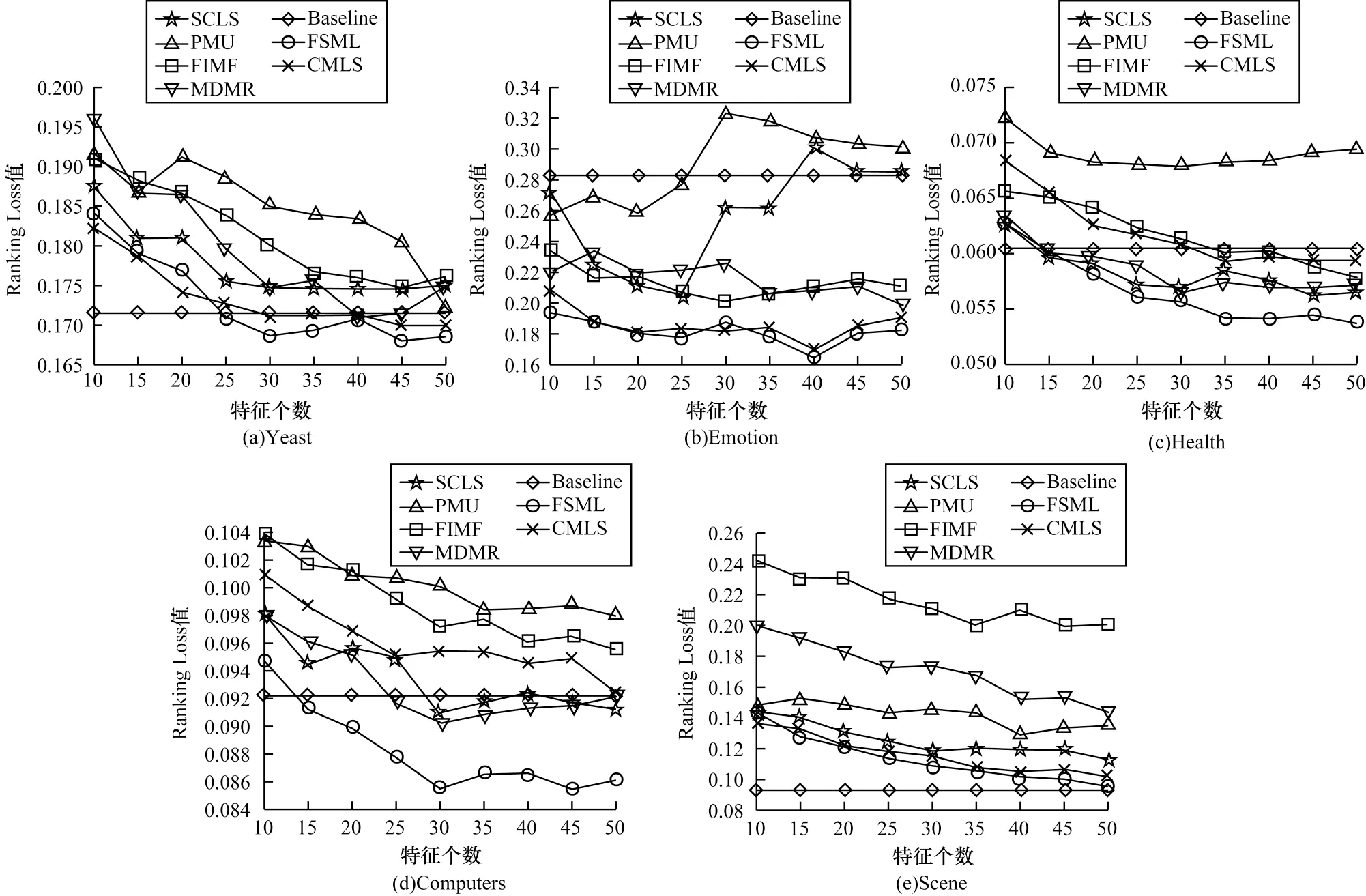
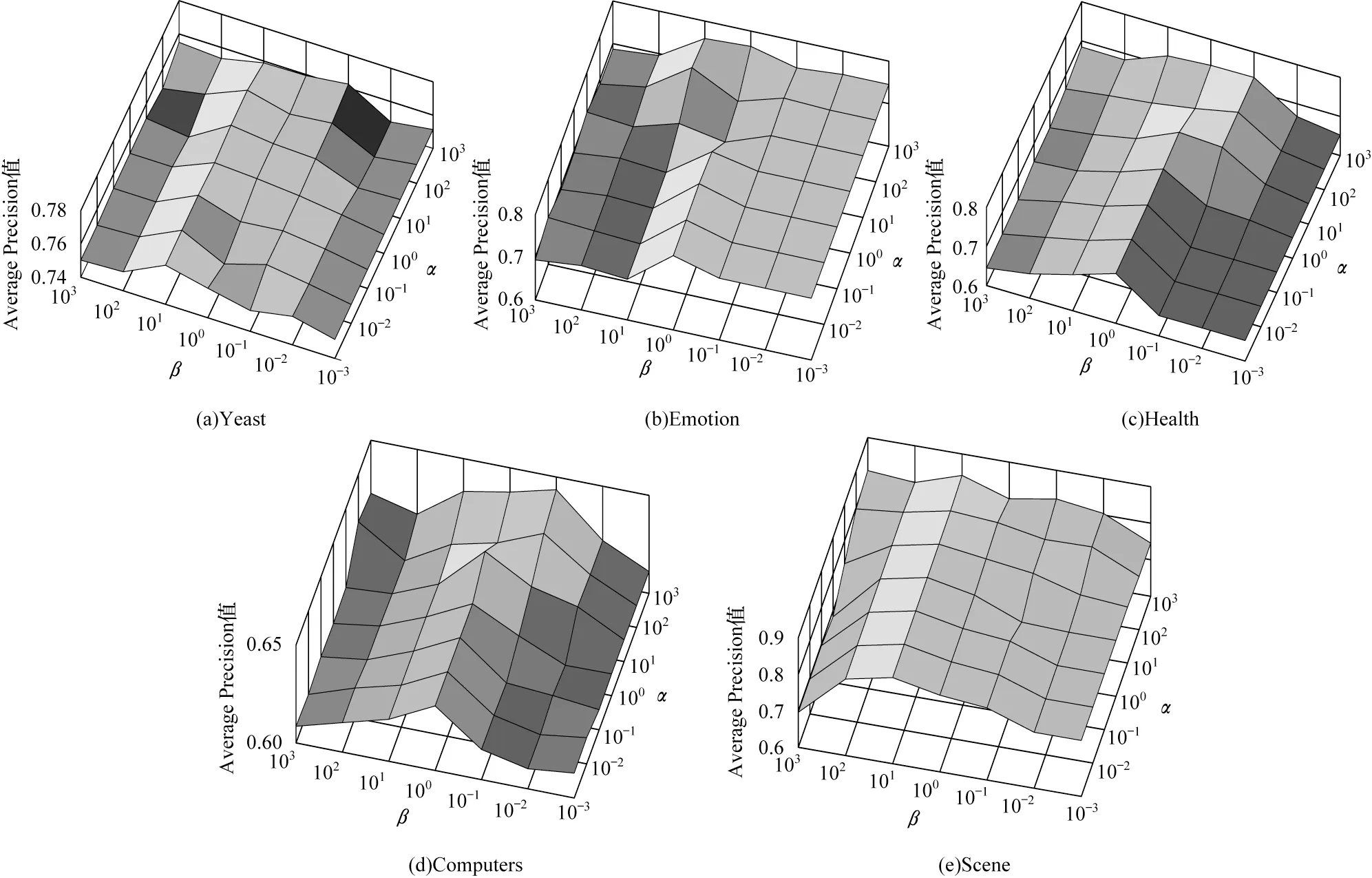
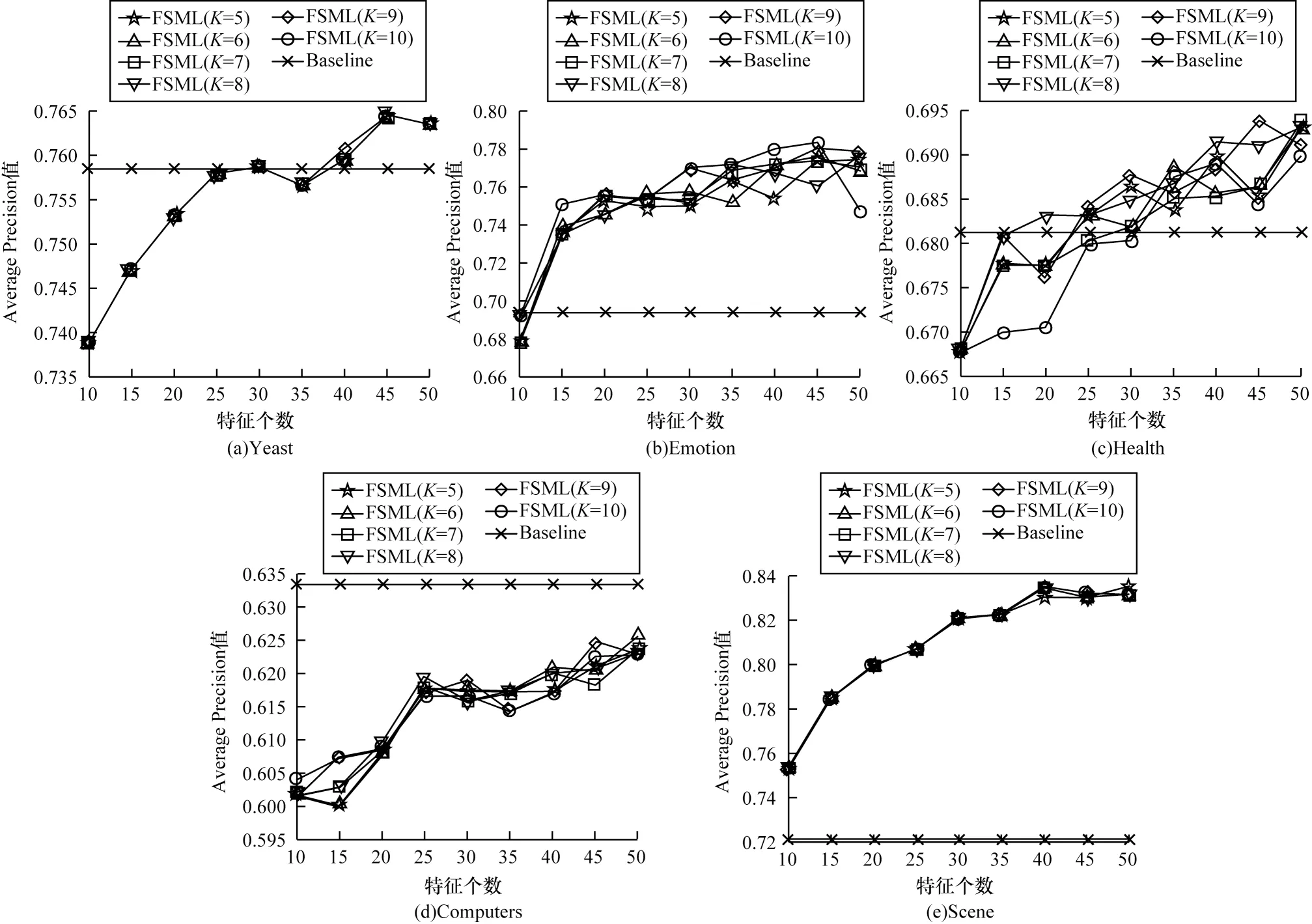
由于多标签分类数据的连续性与标签的离散性,因此一些学者认为多标签数据中,数据与标签的关系可以用logistic 回归模型来学习,并通过不同正则项的约束来改进算法的性能,从而进行多标签特征选择。文献[6]提出一种用于多标签图像分类的相关logistic 回归模型(CorrLog),将传统的logistic回归模型扩展到多标签情况。文献[7]提出混合整数优化logistic 回归的特征子集选择算法,给出一个混合整数线性优化问题,使用标准的整数优化软件求解,并对logistic 回归的损失函数进行分段线性逼近。文献[8]提出一种基于Lq(0 近年来,流形学习快速发展,并逐渐渗透到人们生活以及工业生产等各个领域。为了能够学习到数据特征的基层流形结构,文献[9-10]提出流形学习方法,发现在特征选择的过程中,特征流形结构能够促使特征选择学习到更优的回归系数矩阵。文献[11]提出一个图形学习框架来保持数据的局部和全局结构,该方法利用样本的自表达性来捕获全局结构,使用自适应邻域方法来保持局部结构。文献[12]提出一种新的鲁棒图学习方法,该方法通过自适应地去除原始数据中的噪声和错误,从真实的噪声数据中学习出可靠的图。文献[13]通过数据的自表示性质构建相似矩阵,并运用流形结构和稀疏正则项来约束相似矩阵,从而构建无监督特征选择模型。文献[14]通过将其定义的代价距离代入现有的特征选择模型中,并使用流形结构约束得到一个新的代价敏感特征选择方法。文献[15]使用logistic回归模型,并利用标签流形结构与L1-范数约束回归系数矩阵,构造半监督多标签特征选择模型。可见,流形学习不一定作为正则项来约束回归系数,标签流形学习也是一种学习数据与标签间关系的方法。为找出数据与标签间的关系,准确去除不相关的特征和冗余特征,本文融合logistic 回归模型学习到的系数矩阵和标签流形模型学习到的权重矩阵,基于L2,1-范数提出一种高效的柔性结合标签流形结构与logistic 回归模型的多标签特征选择算法(FSML)。 样本xi不属于第j类的后验概率如下: 其中:wj是系数矩阵W∈Rd×m的第j列向量。 使用极大似然估计法对系数矩阵进行估计,则logistic 回归关于多标签数据集的似然函数(联合概率分布)如下: 由于求解式(3)较为困难,因此可以将式(3)转化为利用求解logistic 回归的负对数似然函数式(4)的极小值来求解W。 又因为logistic 回归模型可能会出现过拟合、多重共线性、无限解等不适定问题,所以导致系数矩阵估计不正确[16]。为了解决这一问题,一种广泛使用的策略是在式(4)中引入稀疏惩罚项,因此带有惩罚项的logistic 回归模型的表达式如下: 其中:β是惩罚因子;R(*)是惩罚函数,表示对*的相应约束惩罚。 近年来,流形学习被广泛应用于协同聚类[17]、特征选择、维数约简[18]等任务中。在特征选择算法中,流形学习通常是被用作正则项来约束回归系数矩阵,以便回归系数矩阵拟合数据特征的基层流形结构,但流形学习在特征选择算法中的使用方式并不局限于此。 在本文研究中,将使用流形学习来拟合数据特征的权重矩阵,为学习得到更好的特征权重矩阵并更有效地利用标签信息,进行如下假设: 1)通过学习数据间的相似矩阵Z来探究数据基层结构。例如,标签相似矩阵Z可以通过核函数学习,如式(6)所示: 其中:Zij是Z的第i行、第j列的元素,表示yi和yj之间的相似度。 2)通过学习得到标签F。因为F需要拟合原始标签Y的基层结构,所以 3)理论上认为:F=XU,其中U∈Rd×m是数据特征的权重矩阵。 根据以上假设构建标签流形学习模型,其表达式如下: 同样地,引入相应的惩罚项,以便在学习过程中约束特征权重矩阵,使其能够很好地拟合标签的基层流形结构。因此,标签流形学习模型也可写成以下形式: 通过式(5)和式(8)可以看出,针对特征选择中的惩罚函数R(*),具有如下要求: 1)惩罚函数R(*)能够约束稀疏矩阵W和权重矩阵U的稀疏性。 2)惩罚函数R(*)能够根据特性结合稀疏矩阵W和权重矩阵U,且能使两者相互促进,相辅相成。 3)在一般情况下,在特征选择的过程中要能够清晰地区分特征的好坏,通常要求能够代表特征的矩阵要行内稳定、行间稀疏。因此,惩罚函数R(*)也要有这种约束性。 选取L2,1-范数作为惩罚函数,即R(*)=‖ * ‖2,1,不仅可以满足要求1和要求3,而且对奇异值比较敏感[19]。 根据要求2,考虑到稀疏矩阵W和权重矩阵U较为相似,且都能用于进行特征选择,初步认为*=W-U,但*=W-U表示两者几乎完全相同,而实际上两者还是有一定的差别,仅基于不同的模型,W与U就会出现差别。引入偏置矩阵1dbT∈Rn×m来使模型变得更为合理,其中,1d∈Rd为使元素全为1 的列向量,b∈Rm为偏置向量。进一步认为*=W+1dbTU,因此R(*)=‖W+1dbT-U‖2,1。 综上,本文设计柔性结合标签流形结构与logistic 回归模型的多标签特征选择算法FSML,其目标优化问题可以改写如下: 其中:α为标签流形参数。 针对L2,1-范数的求解,根据文献[20],当(W+1dbTU)i≠0时,其中i=1,2,…,d。‖W+1dbT-U‖2,1对W或对U的求导也可以看作Tr((W+1dbT-U)TH(W+1dbTU))对W或对U的求导,其中H∈Rd×d是对角矩阵,H的第i个对角元素如下: 因此,可以利用上述优化问题来求出式(9)的近似解,从而将目标函数转变如下: 对于该问题,可给定一个H,将W、U与当前的H进行计算,然后根据当前计算出的W、U对H进行更新。 根据式(11),当固定H和W时,关于U和b的目标函数可改写如下: 根据式(11),当固定H和U时,关于W的目标函数可改写如下: 由于式(17)是可微的,因此可以通过Newton-Raphson 算法进行求解,式(17)对W的一阶导如下: W更新公式如下: 通过以上问题的优化与求解,柔性结合标签流形结构与logistic 回归模型的多标签特征选择算法FSML 具体描述如下: 算法1FSML 算法 FSML 算法的目的主要是计算并更新W与U,每次迭代的时间复杂度为O(2d2n),共迭代t次,因此总的时间复杂度为O(2td2n)。由于t值一般不大,因此FSML 算法处理数据的运行时间受数据维数d和数据集样本个数n的影响较大。 FSML 算法的收敛性分析类似于L2,1-范数的收敛性分析,图1 给出了参数α=1、β=1、K=5 时,FSML 算法在生物数据集Yeast、文本数据集Health和Computers、音乐数据集Emotion、图像数据集Scene 等5 个经典数据集上的收敛性结果。 图1 FSML 算法在不同数据集上的收敛性结果Fig.1 Convergence results of FSML algorithm on different datasets 采用5 个经典数据集进行FSML 算法有效性验证,并将其与SCLS[21]、MDMR[22]、PMU[23]、FIMF[24]、CMLS[25]算法以及Baseline(选择所有特征)进行性能比较,同时选择ML-KNN[26]算法作为代表性的多标签分类算法进行实验。 实验中采用的5 个经典数据集来自木兰图书馆(http://mulan.sourceforge.net/datasets.html),具体信息如表1 所示。 表1 数据集信息Table 1 Dataset information 实验操作系统环境为Microsoft Windows 7,处理器为I ntel®CoreTMi5-4210U CPU@1.70 GHz 2.40 GHz,内存为4.00 GB,编程软件为Matlab R2016a。 实验参数设置如下(设置1 和设置2 均为对应算法的默认设置): 1)在ML-KNN 算法中,设置平滑参数S=1,近邻参数K=10。 2)在FIMF、MDMR 和PMU 算法中,利用等宽区间对数据集进行离散化处理[27],并且在FIMF 算法中,设置Q=10、b=2。 3)将所有特征选择算法(除ML-KNN 算法以外)的最近邻参数设为K=5,最大迭代次数设为50。 4)所有算法的正则化参数通过网格搜索策略进行调整,搜索范围设置为[0.001,0.01,0.1,1,10,100,1 000 ],并将选择的功能数量设置为[10,15,20,25,30,35,40,45,50 ]。 与单标签学习系统的性能评价不同,多标签学习系统的评价指标更为复杂。假设一个测试数据集,给定测试样本di,多标签分类器预测的二进制标签向量记为h(di),第l个标签预测的秩记为ranki(l)。 1)汉明损失(Hamming Loss)。度量的是错分的标签比例,即正确标签没有被预测以及错误标签被预测的标签占比。值越小,表现越好。Hamming Loss 计算公式如下: 其中:Δ 表示两个集合的对称差,返回只在其中一个集合中出现的那些值;HHammingLoss(D) ∈[0,1]。 2)排名损失(Ranking Loss)。度量的是反序标签对的占比,即不相关标签比相关标签的相关性还要大的情况。值越小,表现越好。Ranking Loss 计算公式如下: 3)1-错误率(One-Error)。度量的是预测到的最相关的标签不在真实标签中的样本占比。值越小,表现越好。One-Error 计算公式如下: 4)覆盖率(Coverage)。度量的是排序好的标签列表平均需要移动多少步才能覆盖真实的相关标签集。值越小,表现越好。Coverage 计算公式如下: 其中:CCoverage(D) ∈[0,m-1]。 5)平均精度(Average Precision)。度量的是比特定标签更相关的那些标签的排名占比。值越大,表现越好。平均精度计算公式如下: 本文提出的FSML 算法在5 个经典数据集上进行实验,并考虑Hamming Loss、Ranking Loss、One-Error、Coverage、Average Precision 评价指标对FSML 算法与对比算法的性能进行比较。表2~表6 给出了所有特征选择算法在最优参数时的最优结果,其中,最优结果用粗体标出,次优结果用下划线标出。从表2~表6 可以看出:大多数的最优结果出现在FSML 算法上,从而证明FSML 算法的可行性;具体而言,FSML 算法虽然在Scene数据集上的所有指标相对于Baseline均略有不足,但在Computers、Health、Scene 数据集上的所有指标,以及Yeast数据集上的Ranking Loss、One-Error、Coverage、Average Precision 均优于对比算法,并且在Emotion、Computers、Health、Yeast 数据集上的所有指标甚至优于Baseline。 表2 各数据集上不同算法的Hamming Loss 数据对比Table 2 Data comparison of Hamming Loss among different algorithms on various datasets 表3 各数据集上不同算法的Ranking Loss 数据对比Table 3 Data comparison of Ranking Loss among different algorithms on various datasets 表4 各数据集上不同算法的One-Error 数据对比Table 4 Data comparison of One-Error among different algorithms under various datasets 表5 各数据集上不同算法的Coverage 数据对比Table 5 Data comparison of Coverage among different algorithms on various datasets 表6 各数据集上不同算法的Average Precision 数据对比Table 6 Data comparison of Average Precision among different algorithms on various datasets 综上,FSML 算法在各种实验指标上的性能均明显优于FIMF 算法、PMU 算法、MDMR 算法和SCLS 算法,在Computers、Health、Scene 数据集上明显优于CMLS 算法,在Emotion 数据集上略优于CMLS 算法,并在除Scene 数据集以外的其他实验数据集上的指标均优于Baseline。 为能更直观地展示FSML 算法与对比算法以及Baseline 的性能对比,图2~图6 给出了所有算法在各种数据集上的性能评价指标。从图2~图6 可以看出:FSML 算法在Scene 数据集上的性能表现虽然略次于Baseline,但在其他数据集上的性能表现很好,尤其是在Health 数据集上的性能表现最好,明显优于对比算法和Baseline。通过FSML 算法与对比算法的比较结果可以看出,FSML 算法的实验结果通常优于对比算法,可见将logistic 回归模型与流形结构柔性结合,能更准确地学习到数据与标签间的关系;通过与Baseline 的比较结果可以看出,FSML 算法在大多数数据集上的实验结果都优于Baseline,能够有效去除不相关的特征和冗余特征。 图2 各数据集上不同算法的Hamming Loss 曲线对比Fig.2 Curve comparison of Hamming Loss among different algorithms on various datasets 图3 各数据集上不同算法的Ranking Loss 曲线对比Fig.3 Curve comparison of Ranking Loss among different algorithms on various datasets 图4 各数据集上不同算法的One-Error 曲线对比Fig.4 Curve comparison of One-Error among different algorithms on various datasets 图5 各数据集上不同算法的Coverage 曲线对比Fig.5 Curve comparison of Coverage among different algorithms on various datasets 图6 各数据集上不同算法的Average Precision 曲线对比Fig.6 Curve comparison of Average Precision among different algorithms on various datasets 为研究FSML 算法对参数的敏感程度:一方面,设置近邻参数K=5,通过网格搜索策略来调整α与β的数值,探究FSML 算法在取不同参数时,Average Precision 评价指标的变化情况,如图7 所示,可以看出在一定范围内Average Precision 评价指标值会随参数的变化而变化,并且不同的实验数据对参数的敏感程度不同,当α<1、β<1 时FSML 算法性能对参数的变化不是很敏感;另一方面,设置参数α=10、β=100,在[5,6,7,8,9,10]内调整近邻参数K的值,探究近邻参数K的变化对FSML 算法性能的影响,如图8 所示,可以看出在Yeast、Scene 数据集上FSML 算法对近邻参数K的变化不太敏感,而在其他数据集上则较为敏感,可见FSML 算法对近邻参数K的变化是否敏感与数据本身的基层结构特征有关。 图7 参数α、β 对FSML 算法的影响Fig.7 Influence of parameters α and β on FSML algorithm 图8 近邻参数K 对FSML 算法的影响Fig.8 Influence of parameter K on FSML algorithm 如图9 所示,横坐标轴表示在各评价指标下各多标签特征选择算法的排序,从左到右,算法的性能越来越好,同时还给出了Bonferroni-Dunn 测试结果的平均秩图,并将无显著差异(p<0.1)的算法组连接,如果平均排名达到差异的临界值(Critical Distance),则有显著差异[28]。在One-Error 指标下,FSML 算法性能明显优于对比算法,并具有显著性差异;在其他指标下,FSML 算法的性能明显优于SCLS、FIMF、MDMR 和PMU 算法,并具有显著性差异,虽然与CMLS 算法之间没有显著性差异,但FSML 算法的排序始终在第一位。因此,与其他算法相比,FSML 算法具有更好的性能。 图9 Bonferroni-Dunn 检验结果的平均秩图Fig.9 Average rank graph of Bonferroni-Dunn test results 本文基于L2,1-范数将标签流形结构与logistic 回归模型柔性结合,构建多标签特征选择算法FSML,并在多个经典多标签数据集上与现有多标签特征选择算法进行性能对比。实验结果证明了FSML算法的有效性。但由于近邻参数K不能自适应学习,导致同一个K值不一定能够较好地学习到每个数据标签的基层流形结构,从而限制了FSML 算法的应用范围。下一步将对相似矩阵学习进行研究,使近邻参数K能够实现自适应学习,并扩展该自适应学习方法在半监督多标签特征选择中的应用与研究。1 模型建立
1.1 logistic 回归模型
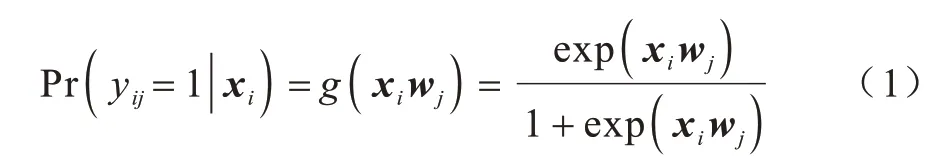



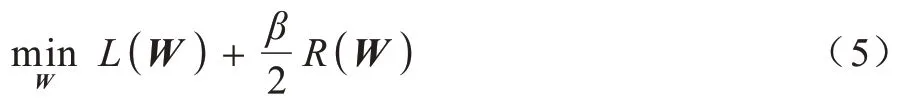
1.2 流形学习
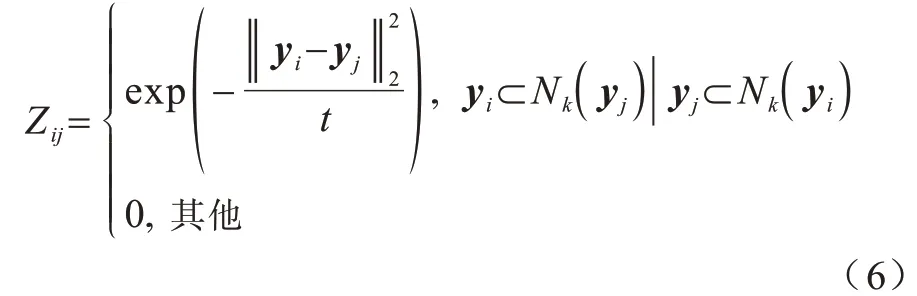


1.3 柔性嵌入

2 问题求解
2.1 问题优化


2.2 给定H、W 的U 求解

2.3 给定H、U 的W 求解
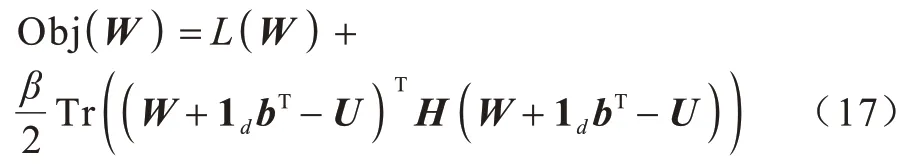
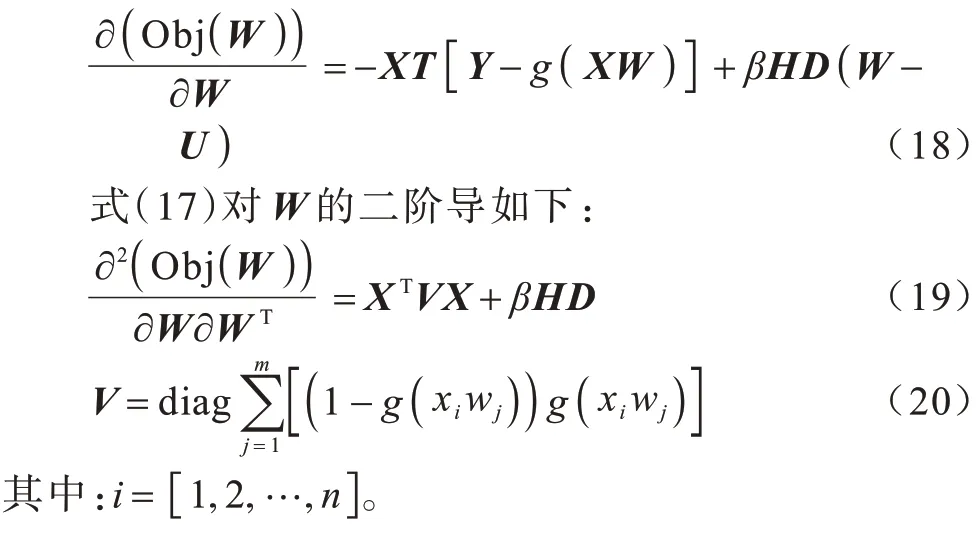
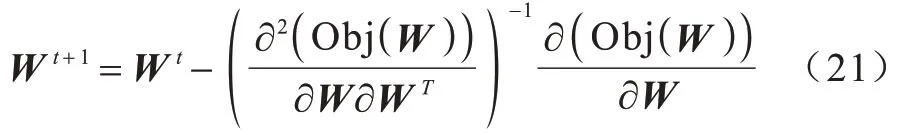


3 实验与结果分析
3.1 数据集与实验设置

3.2 评价指标
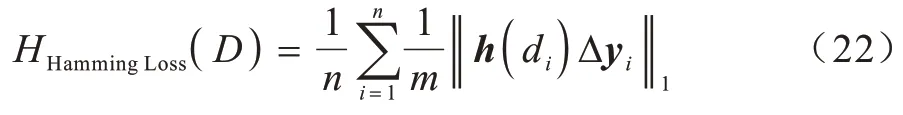
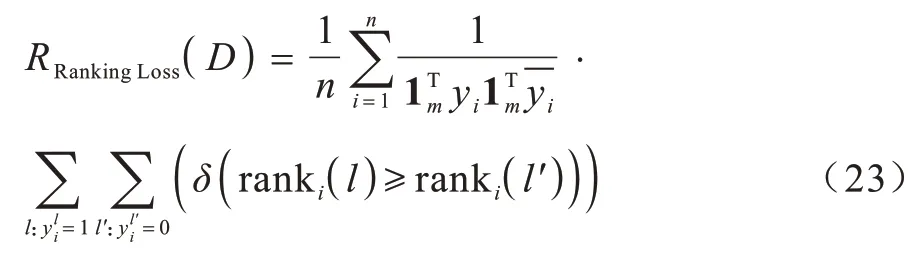
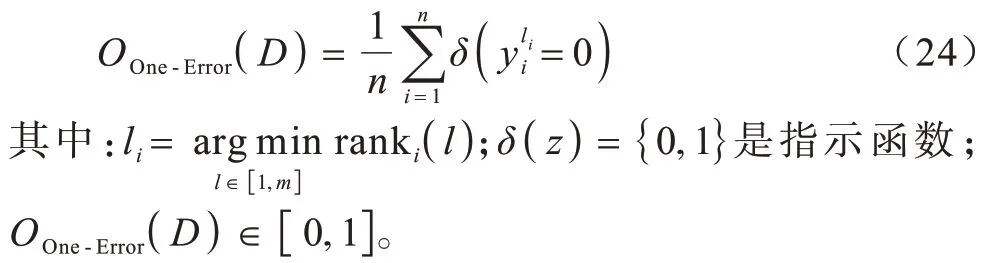

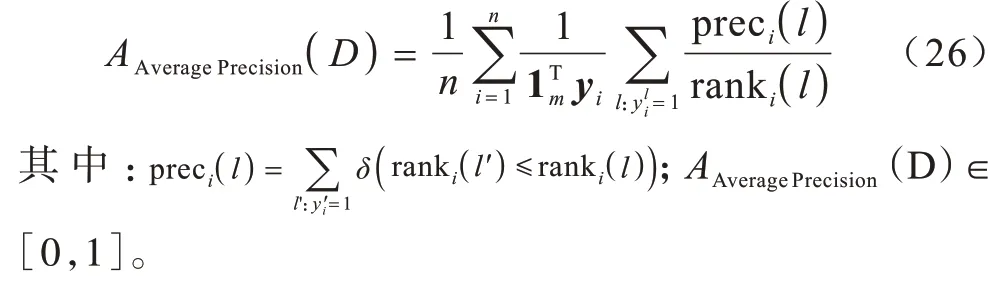
3.3 实验结果



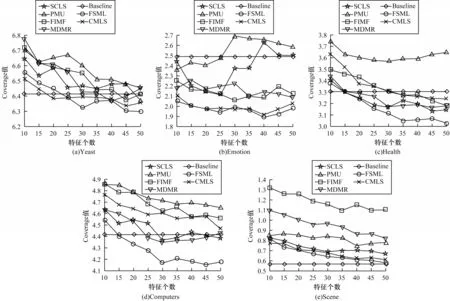
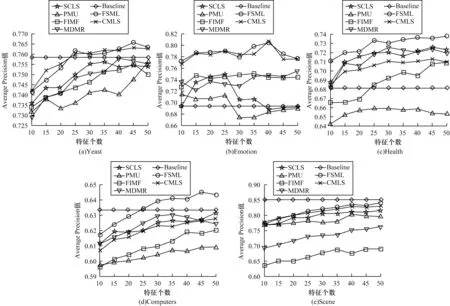

4 结束语
