浅谈材料力学冲击应力分析的基本假设1)

刘 华 周思聪

(北京航空航天大学航空科学与工程学院，北京 100191)

能量法在材料力学中有着广泛的应用，例如确定理想弹性压杆的临界挠度[1]，计算桁架结构的受力[2]等。能量法还可以用于冲击应力分析，利用冲击过程中的能量转换关系，即冲击物的机械能全部转换为被冲击物的应变能，建立方程并求解被冲击物的最大冲击应力。该理论采用如下基本假设[3]：(1) 冲击物为刚体；(2) 被冲击物的质量忽略不计；(3) 冲击物与被冲击物接触后始终保持接触；(4)冲击过程中的能量损失忽略不计。这些假设大大简化了实际冲击过程中复杂的应力、应变变化过程，是工程中冲击问题的简化计算方法。在教学过程中发现，学生往往将注意力集中于公式的推导，忽略或不能够准确理解基本假设在该问题中的重要性。本文旨在通过一个算例增进学生对能量法中基本假设的理解，了解和掌握材料力学中用能量法进行冲击应力分析的适用范围，引导学生对教材内容进行思考。

1 能量法基本假设的意义

工程中的结构常遭受冲击载荷作用，与静载荷不同的是，冲击载荷引起的应力不会立即传至被冲击物的各个部位。当冲击速度较低时，冲击物引起的扰动以弹性波的形式在被冲击物内传播。在扰动信号未到达之前，被冲击物离冲击部位较远的位置保持静止。当冲击速度不断增加时，由塑性材料制成的被冲击物产生塑性变形，甚至表现出流体和气体特性。材料力学中的研究对象为弹性材料，故在此仅考虑低速撞击，不考虑塑性等复杂的动力学响应特性。

由于冲击问题的复杂性，在材料力学中，需采用一些基本假设对问题进行简化并构建相应的力学模型。当冲击物的变形可忽略不计时，可将其视为刚体，即假设(1) 旨在保证冲击物的应变能可被忽略。由弹性动力学理论可知，弹性波在固体介质中的传播条件为介质具有可变形性和惯性效应。当被冲击物的质量相对于冲击物质量较小时，可忽略其惯性效应，因此弹性波传播的波动特性被忽略，冲击载荷引起的应力可瞬间传遍整个被冲击物，动力学问题被视为静力学问题，被冲击物的动能被忽略。因此，当冲击载荷获得最大值时，冲击应力、冲击位移和冲击应变也均获得最大值，即假设(2) 旨在保证被冲击物的惯性效应和动能可被忽略。若冲击物与被冲击物在冲击过程中不发生分离，当冲击物的速度减小为零且不考虑冲击过程中热能等能量的损失时，冲击物减小的机械能将全部转换为被冲击物的应变能，由此可依据能量守恒计算出最大冲击应力、最大冲击载荷等，即假设(3)和(4)旨在简化能量的转换关系。

2 算例分析

本文以杆件承受轴向撞击这一简单的力学问题为例进行分析。如图1 所示，质量为M2的圆截面杆左端自由右端固定，质量为M1的刚体以初始速度V0= 5 m/s 水平撞击杆的左端，杆只产生弹性变形且不发生屈曲，杆长L2= 0.5 m，截面半径R2= 0.01 m，密度ρ2= 7.8 kg/m3，弹性模量E2=205 GPa。

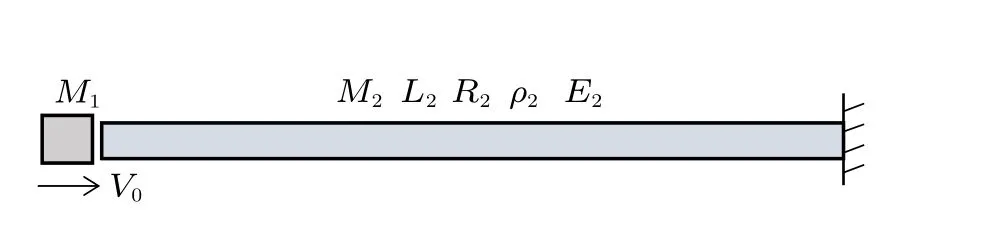
图1 杆件受轴向冲击示意图

图2 杆内应力波传播示意图

其中，σn(t)为第n个周期中杆端的接触应力，Sn(t)的表达式为

图3 对比了弹性动力学理论解与有限元数值解，可以看出该理论能够真实地反映第一次撞击接触应力的变化过程。如图3(a)所示，当m=0.7 时，刚体与杆件在第二周期内分离。通过理论计算表明，对于m< 1 的所有情况，刚体与杆件均在第二周期内分离。如图3(b) 所示，在m= 1 时，刚体与杆件发生了二次撞击，二次撞击的接触应力峰值小于第一次撞击。为了避免冲击物与被冲击物在撞击后分离，可以通过安装飞射物回收装置[5]等方式，使刚体附着在杆端并与杆件一起做往复振动，但这对本问题关注的最大接触应力影响很小，故本文未对这一现象进行详细讨论。若弹性动力学理论预测的整个冲击过程中的最大接触应力记为σmax，由图3(c) 可知，当m= 14 时，σmax= 4.75σ0，出现在3T时刻，刚体与杆件于5.7T时刻分离。由图3(a)～图3(c) 可见，随着m的增大，刚体与杆件分离所需要的周期数随之增多。如图4 所示，与静力学问题不同，惯性力的存在使得接触端的最大冲击位移与最大接触应力并不出现在同一时刻。

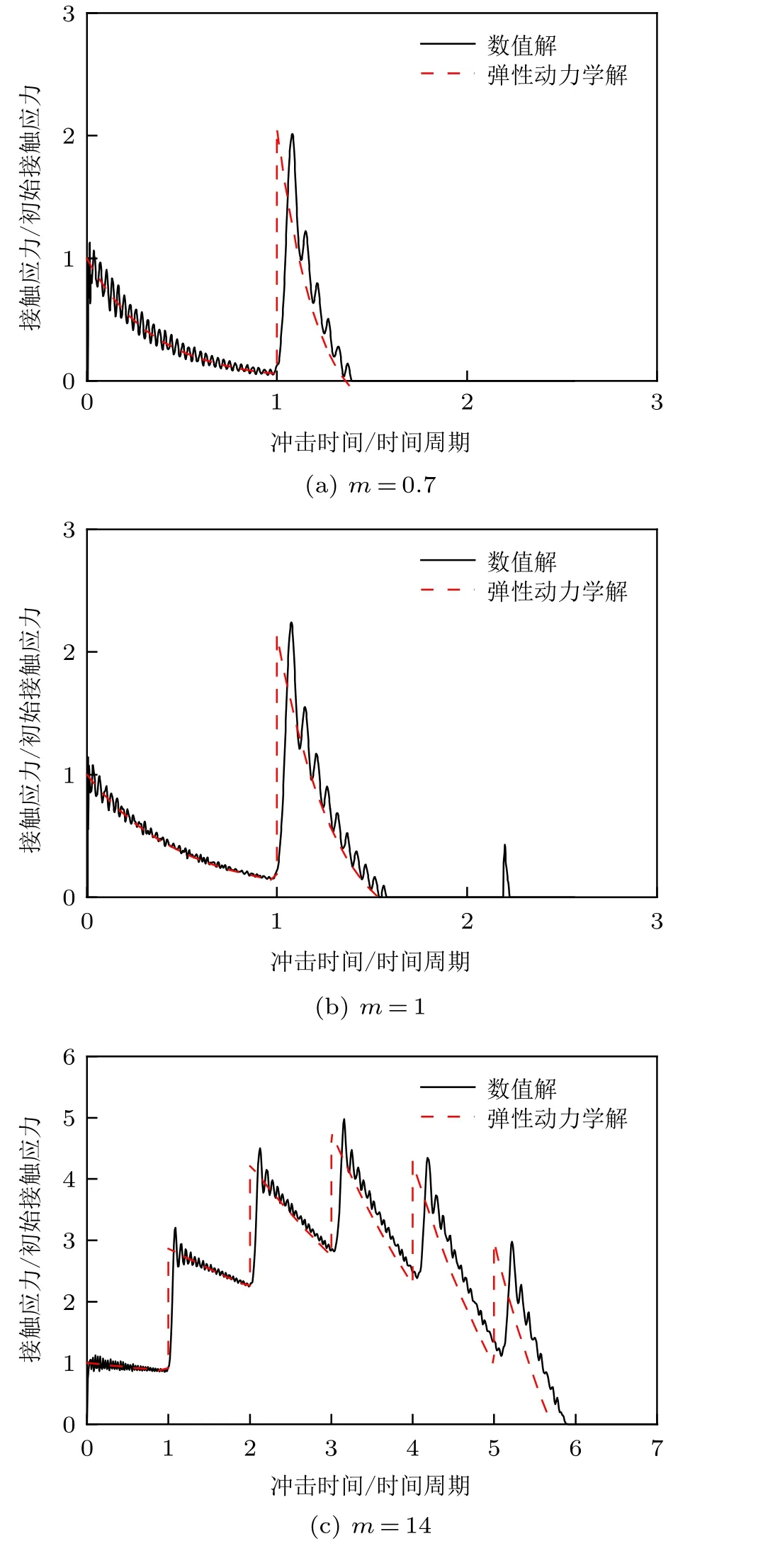
图3 不同质量比时弹性动力学解与有限元数值解对比

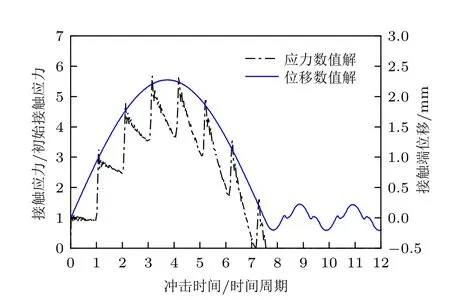
图4 质量比m=21 时接触应力、接触端位移时间曲线

材料力学中的能量法不能描述整个冲击过程，只能依据冲击物的动能全部转化为被冲击物的弹性应变能这一条件，在被冲击物变形达到最大时，求得杆内的最大动应力σd,max为

在本问题中，由于基于能量法给出的动应力在杆内为常值，所以该应力亦为冲击物与被冲击物之间的最大接触应力。

对比式(2) 和式(4) 可知，对于给定的杆件，σd,max/σmax与质量比m有关。表1 对比了不同质量比情况下，σd,max与σmax及有限元方法预测的最大接触应力σFE,max的比值关系。由表可知，随着质量比m的增大，能量法的结果越来越接近弹性动力学理论和有限元方法预测的结果。这是因为当冲击物的质量相对于被冲击物的质量越来越大时，因忽略被冲击物的质量所带来的误差影响会越来越小，更加接近于能量法的假设(2)情况。由此可知，只有当实际情况越符合材料力学能量法所给的假设情况时，依据能量法计算得到的结果越精确。可以推论，当质量比越来越大时，能量法求得的最大接触应力与弹性动力学理论解的比值将趋向于1，但总是小于1。

表1 质量比对σd,max/σmax 和σd,max/σFE,max 的影响

在图5 中，给出了当质量比m变化时，材料力学能量法和弹性动力学理论预测的最大接触应力。可以发现，除去质量比趋近于零的区域，对于给定的m，材料力学预测的最大接触应力与弹性动力学理论值的差值约为1，即两者求得的最大接触应力相差一个初始接触应力。基于此，对本问题中材料力学的结果进行修正，即在原解的基础上加上初始接触应力，则式(4) 变为

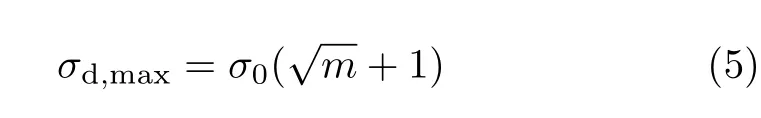
由图5 可见，修正后的材料力学能量解与弹性动力学理论解几乎重合，有兴趣的同学可以想一想为什么会出现这种情况，是巧合还是有某种原因呢？

图5 不同方法预测的最大接触应力-质量比曲线

3 结语

实际的冲击问题会涉及冲击物的变形及反弹、冲击物与被冲击物的二次撞击、被冲击物的振动等力学现象，很难满足材料力学能量法中的全部基本假设。本文仅对杆件承受轴向撞击这一简单的冲击问题进行了研究，对于材料力学中更复杂的冲击问题也可做类似研究，以揭示更多的力学现象和规律。一个力学模型所采用的基本假设恰恰限定了该理论的适用范围，材料力学中的能量法只能对冲击问题以“静” 代“动” 进行近似分析。当实际的冲击问题与基本假设相去甚远时，运用该理论预测的结果必定误差较大。在材料力学的教学过程中，教师应当重视对基本假设的讲解和培养学生根据实际问题抓住主要矛盾进行合理假设和简化的能力，这对于学生分析和解决实际工程问题是非常重要的。