5—6岁儿童模式能力的发展特点及教育建议

田方 王娜 蔺卫玲

【摘要】本研究随机选取上海市、西安市281名5—6岁儿童作为研究对象，测量其模式能力的发展情况。研究结果表明：5—6岁儿童具有较高的重复性模式水平，其发展性模式水平还有待提高;儿童对发展性模式的理解呈现出4种认知水平，分别是前结构性意识、结构意识模糊、部分结构性意识、结构性意识。研究者据此提出建议。

【关键词】5—6岁儿童;重复性模式;发展性模式;模式能力

【中图分类号】G610 【文献标识码】A   【文章编号】1004-4604（2022）03-0030-06

模式是早期数学教育的重要组成部分，重复性模式和发展性模式对儿童日后代数能力和数学思维的发展具有积极影响。已有研究多关注学前儿童的重复性模式能力，较少探究学前儿童的发展性模式能力。本研究拟探讨5—6岁儿童两种模式能力的发展特点，以期为幼儿园的教育教学提供参考。

一、研究设计

（一）研究对象

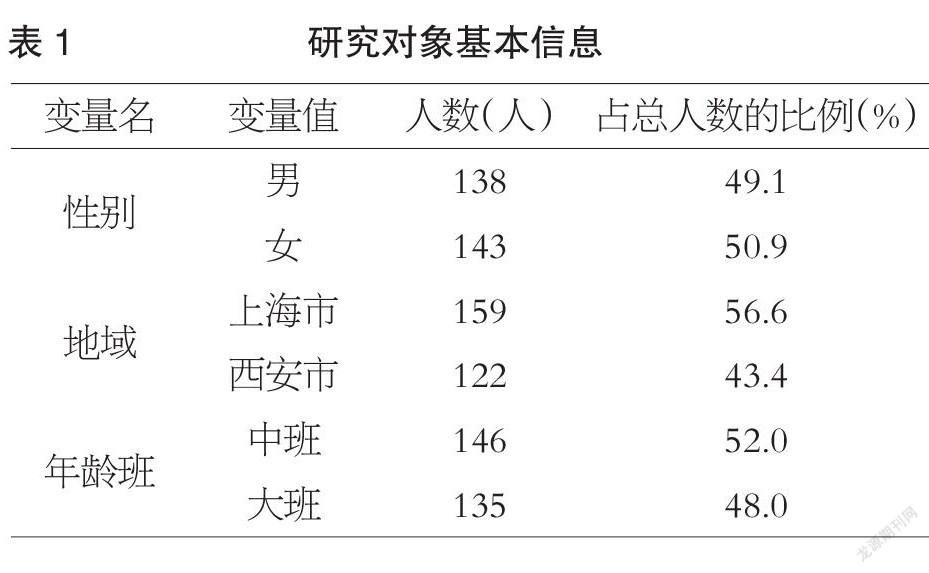
本研究从上海市、西安市各选取3所幼儿园，上海市选取的幼儿园包括1所市级示范性幼儿园、1所市级一级园和1所市级二级园，西安市选取的幼儿园包括1所省级示范性幼儿园、1所省级一级园、1所省级二级园。从6所幼儿园中共随机选取281名中、大班儿童作为研究对象，儿童平均年龄为67.77个月。研究对象基本信息见表1。

（二）研究工具

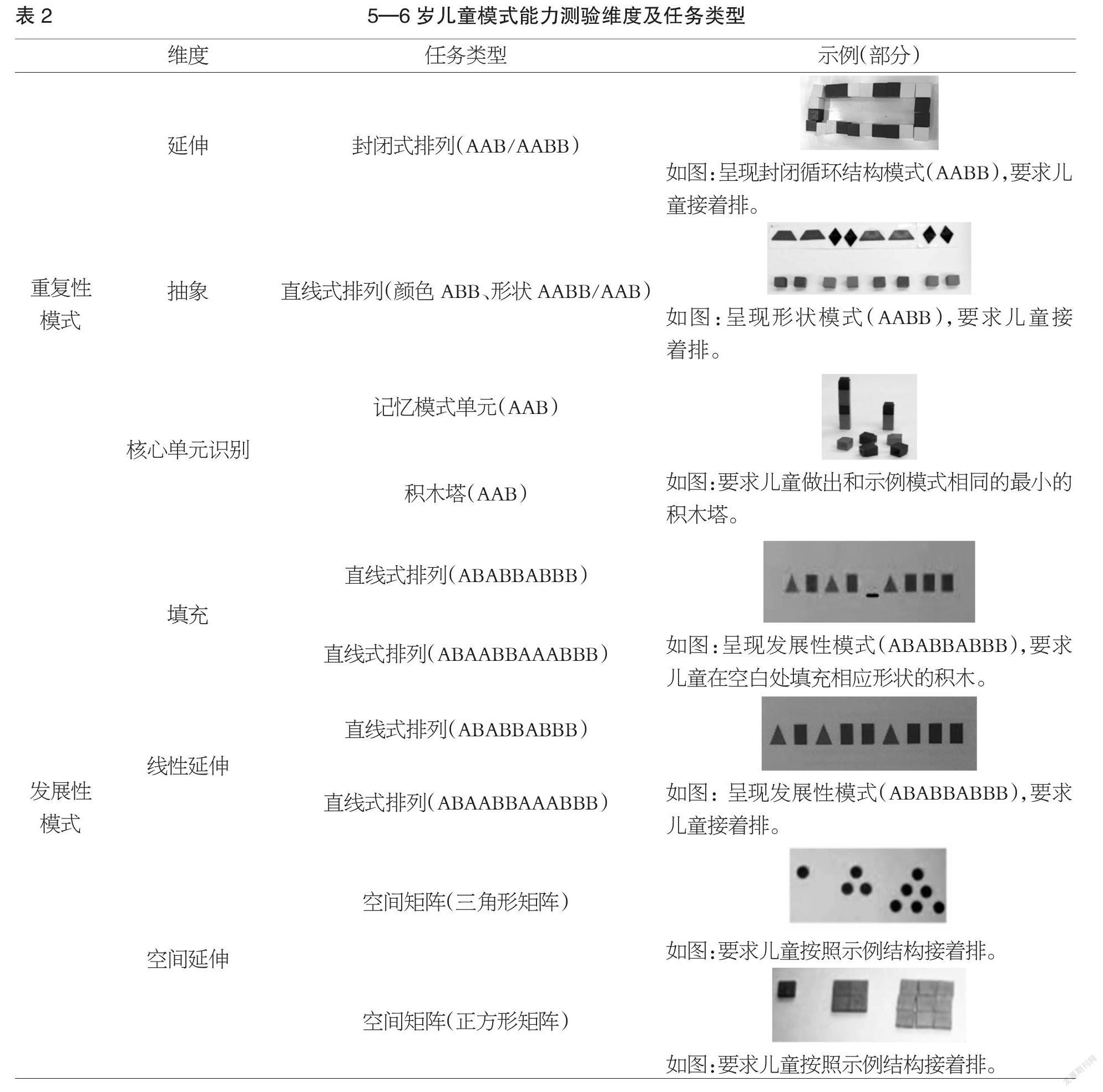
本研究采用《5—6岁儿童模式能力测试》作为测查工具，测量学前儿童模式能力的发展情况。该工具包括重复性模式部分和发展性模式部分。前者采用约翰逊（Rittle-Johnson）等人编制的重复性模式任务，〔1〕后者借鉴帕皮克（Papic）〔2〕和韦恩斯（Wijns）等人〔3〕编制的发展性模式和结构探究的部分任务。其中，重复性模式任务包括延伸、抽象和核心单元识别3个维度，共7个项目;发展性模式任务包括填充、线性延伸和空间延伸3个维度，共6个项目（见表2）。该测试采用0、1计分法，答对计“1”分，答错计“0”分，共13分。经检验，该测试具有良好的信效度。〔4〕

（三）研究过程

本研究由3名接受测试培训的研究者对儿童进行一对一的测试。测试在幼儿园中较为安静的房间内进行，测试期间全程录像。在发展性模式部分的测试中，儿童每完成一个项目，研究者随即对其进行访谈，进一步探究儿童对发展性模式任务的自我解释和认知策略。

（四）数据处理

本研究采用SPSS23.0软件对数据进行处理与分析。此外，由2名研究者参照穆里根（Mulligan）关于儿童早期模式结构水平设计编码框架，〔5〕同时结合临床访谈结果对儿童在发展性模式任务中的错误类型和认知策略进行归类编码。

二、研究结果

（一）5—6岁儿童模式能力发展的总体情况

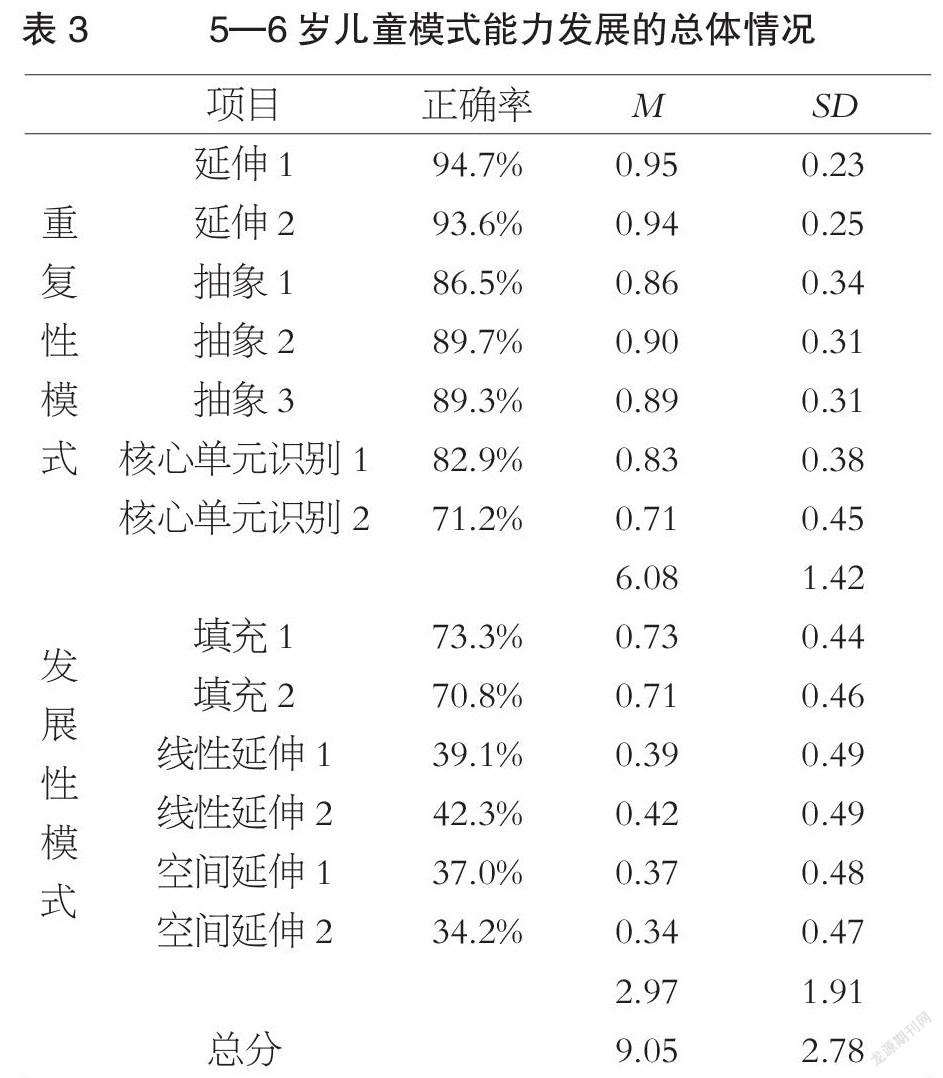
由表3可知，5—6岁儿童在重复性模式部分测试中的表现显著好于发展性模式部分。在重复性模式部分的测试中，儿童在核心单元识别项目上的得分最低。在发展性模式部分的测试中，儿童在各项目上的得分呈现出递减状态，从高到低依次是填充任务、线性延伸任务和空间延伸任务。整体来看，5—6岁儿童发展性模式延伸任务的正确率在43%以下，说明部分儿童具备一定的发展性模式延伸能力，但整体水平较低。

（二）5—6岁儿童发展性模式延伸任务的错误类型

本研究对儿童在发展性模式延伸任务中每一个项目的操作结果进行了记录，对儿童出现错误的反馈进行归纳，确定了兒童线性延伸和空间延伸任务的错误类型编码框架。

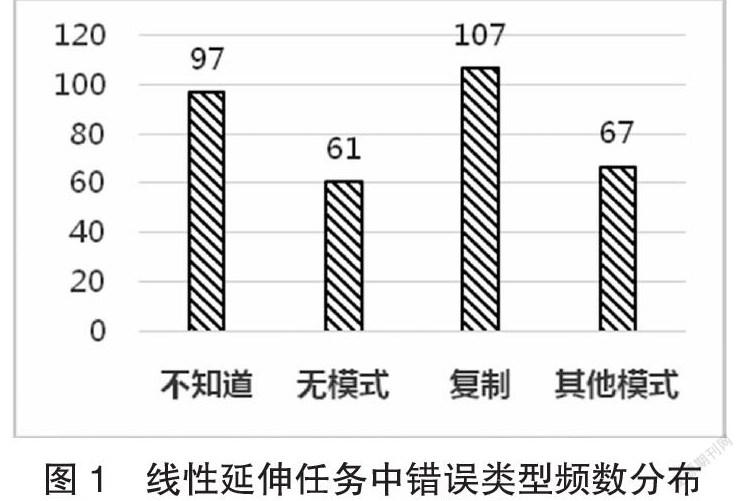
在线性延伸任务中，儿童共出现332个错误。由表4可知，错误类型可归纳为不知道、无模式、复制、其他模式。由图1可知，儿童在线性延伸任务中出现最多的错误类型是复制（n=107），而后是不知道（n=97）、其他模式（n=67）和无模式（n=61）。

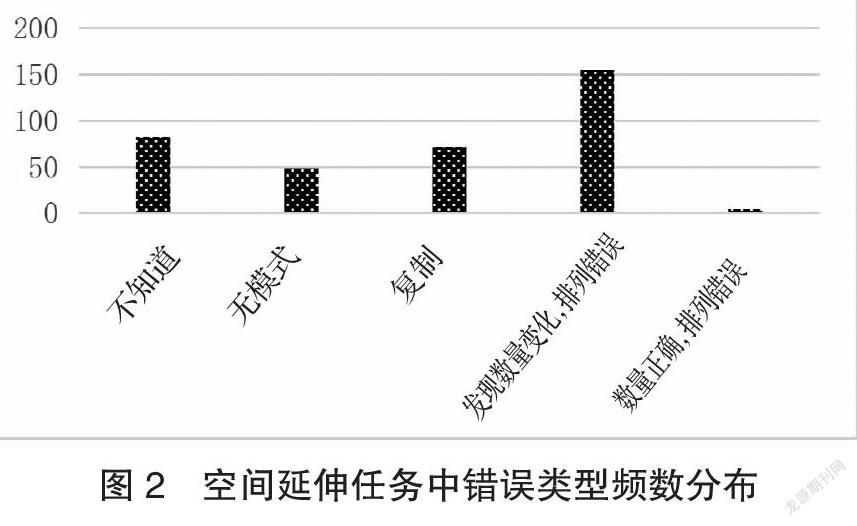
在空间延伸任务中，儿童共出现362个错误。由表5可知，错误类型可归纳为：不知道;无模式;复制;发现数量变化，排列错误;数量正确，排列错误。由图2可知，儿童出现最多的错误类型是“发现数量变化，排列错误”（n=155），最少的是“数量正确，排列错误”（n=4）。

（三）5—6岁儿童发展性模式延伸任务的自我解释类型

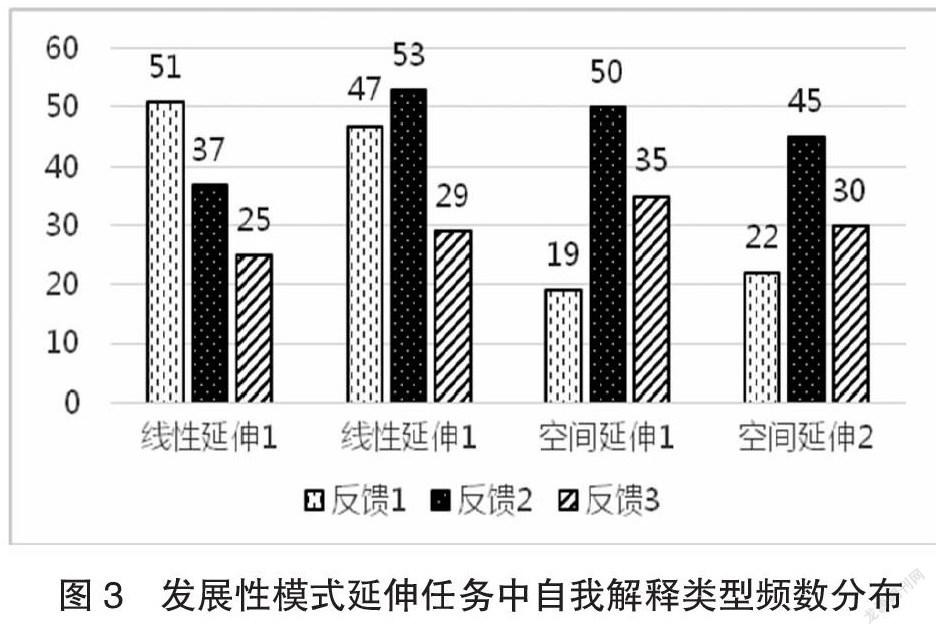
本研究采用访谈法，对在发展性模式延伸任务中排列正确的儿童进行提问，以了解儿童对发展性模式延伸任务的理解及其思考的过程。在与一线教师和专家讨论后，结合穆里根的研究，〔6〕本研究将儿童的自我解释归纳为3种类型，分别是：排列正确，不能解释;发现递增规律，表述不明确;发现内在结构（见表6）。此外，本研究对发展性模式延伸任务中儿童的自我解释类型进行编码统计，共得出443个有效编码。其中，41.76%的儿童能够发现递增规律，表述不明确;31.38%的儿童排列正确，不能解释;26.86%的儿童能够较为明确地描述出发展性模式延伸任务的内在结构。

由图3可知，在线性延伸任务中，出现最多的自我解释类型是“排列正确，不能解释”。在空间延伸任务中，出现最多的自我解释类型是“发现递增规律，表述不明确”。

三、讨论

（一）5—6岁儿童重复性模式能力的特点

本研究结果表明，5—6岁儿童的核心单元识别能力还有待进一步提升。核心单元识别指儿童能发现模式中不断重复的单元，如在AABAAB模式中，核心单元即AAB。核心单元识别要求儿童能够在模式中直接识别并正确地指出核心单元。这就需要儿童考虑核心单元元素的外部属性特征和确切的数量，以及在整个模式中的起始位置，无法借助匹配或对应的策略。从儿童重复性模式能力的发展轨迹来看，识别模式中的重复单元是儿童理解重复性模式的关键。克莱门茨（Clements）等人指出，可能到6岁左右，儿童能够发展识别模式核心单元的能力。〔7〕大多数5—6岁儿童能够发现重复性模式“重复”的本质规律，但常会在识别重复单元的元素组合或起始位置上出现一定的偏差。例如，在AABBAABB模式中，有些儿童可能会指出BBAA是重复单元，或指出AABBAA是重复单元。因此，对于5—6岁儿童来说，识别重复性模式中的核心单元仍是深入理解重复性模式的关键。

（二）5—6岁儿童发展性模式能力的特点

本研究结果表明，儿童在线性延伸任务中的正确率高于空间延伸任务。究其原因，在线性延伸任务中，儿童只需要考虑每种元素的数量变化。例如，在ABABBABBB线性延伸模式中，元素B的数量是逐一增加的。而在空间延伸任务中，元素的数量不是逐一增加的，很多儿童能发现元素的数量变多了，但很难抽象出变化规律。此外，在空间延伸任务中，儿童还要顾及元素结构的变化，这就需要更为复杂的认知策略。

本研究结果表明，在线性延伸任务中，多数儿童会出现“复制”的错误。这说明儿童并没有理解发展性模式的内在结构，仍然按照重复性模式的思维进行排列。在空间延伸任务中，多数儿童能够发现各位置元素的数量变化，但排列错误。综合来看，5—6岁儿童具备一定的发展性模式能力，但容易受重复性模式的思维方式或认知策略影响。

（三）5—6岁儿童发展性模式能力的认知水平

1.前结构性意识

处于前结构性意识水平的儿童，大多只关注到模式中元素的属性特征，不能认识到模式的内在结构。本研究中儿童表现为基于重复性模式的思维来认识发展性模式。

2.结构意识模糊

结构意识模糊指儿童能够发现与发展性模式相关的特征，但不能正确识别。本研究中部分5—6岁儿童能够发现示例中元素数量或空间排列结构上的变化，且能够意识到发展性模式与重复性模式是不同的。然而，在自我解释时，儿童不能确切地说明哪里变了、如何变了。这表明处于这种水平的儿童开始有了关注发展性模式内在结构的意识，但对数量、结构的变化趋势还没有明确的认知。

3.部分结构性意识

部分结构性意识指儿童能够感知发展性模式中各位置元素的数量变化或结构变化。处于这一水平的儿童能够更加清晰地发现发展性模式的变化，对空间结构的感知也更加细致化。儿童在自我解释时，也能够大致说明排列的理由和策略。

4.结构性意识

具有结构性意识的儿童，能够识别发展性模式中各元素的数量变化或结构变化，并发现内在的变化规律。这里的结构性意识不仅仅是指简单地识别模式中的元素或属性，还涉及对这些属性如何应用、呈现或建立关联的方式有更深入的了解。〔8〕

四、教育建议

（一）关注儿童早期模式能力的发展

模式对儿童早期代数思维的发展具有积极作用。在已有的早期数学教育研究中，更多关注的是儿童早期数能力的发展，较少关注儿童模式能力的发展。儿童有大量机会在家庭和幼儿园中接触数学，教师和家长是与儿童最常互动的主体。因此，教师、家长、儿童的互动能有效地促进儿童早期模式能力的发展。儿童在幼儿园学习的有关模式的核心经验，需要在生活中不断应用才能得以巩固。家庭是其经验延伸的重要场域。具体来说，儿童可以在与家长的互动和交流中不断进行自我解释，加深自己对模式的理解。

（二）鼓励儿童进行重复性模式的多元表征

引导儿童对模式进行多种形式的表征，能够有效地提升儿童的模式比较和转换能力，有助于儿童模式抽象能力的发展。早期我们可以先为儿童提供视觉材料表征模式。视觉材料能够清晰、持久地呈现核心单元的迭代，较为直观，便于儿童直接操作。随着儿童年龄的增长，模式经验更加丰富，我们可以为儿童提供听觉模式或者动作模式。多种模式表征方式的提供，可以拓展儿童对不同模式的理解，避免儿童误以为模式只是颜色、形状或大小的线性序列。

（三）在日常生活中逐步滲透发展性模式

学前儿童发展性模式能力与儿童的数学能力存在一定的相关。儿童理解发展性模式，重点在于关注模式中的位置与元素之间的关系。这是儿童代数思维发展的基础。发展性模式较之重复性模式，更为复杂。我们可以在日常生活中逐步引导儿童发现和探究发展性模式的内在结构，并将这种经验迁移至对数结构的理解。在学前期引导儿童了解发展性模式能够促进他们区分模式的不同类型，并进一步发展他们的模式能力。

参考文献：

〔1〕RITTLE⁃JOHNSON B，FYEE E R，MCLEAN L E，et al.Emerging understanding of patterning in 4⁃year⁃olds〔J〕. Journal of Cognition and Development，2013，14（3）：376-396.

〔2〕PAPIC M，MULLIGAN J T.Preschoolers’ mathematical patterning〔R〕.Proceedings of the 28th annual conference of the mathematics，2005.

〔3〕WIJNS N，TORBEYNS J，BAKKER M，et al.Four⁃year olds’ understanding of repeating and growing patterns and its association with early numerical ability〔J〕.Early Childhood Research Quarterly，2019（49）：152-163.

〔4〕田方.4—6岁儿童模式能力的发展及其干预研究〔D〕.上海：华东师范大学，2021.

〔5〕〔6〕MULLIGAN J T，MITCHELMORE M.Awareness of pattern and structure in early mathematical development〔J〕.Mathematics Education

Research Journal，2009，21（2）：33-49.

〔7〕CLEMENTS D H，SARAMA J.Learning and teaching early math：The learning trajectories approach〔M〕.New York：Routledge，2009：189-202.

〔8〕MASON J，STEPHENS M，WATSON A， et al.Appreciating structure for all〔J〕.Mathematics Education Research Journal，2009（2）：10-32.

The Development Characteristics of Children Aged 5-6 and Suggestions

Tian Fang 1， Wang Na 2， Lin Weiling 2

（1 Faculty of Education， Shanxi Normal University， Xi’an， 710062）

（2 Xilan Kindergarten， Xi’an， 710060）

【Abstract】This study randomly selected 281 children aged 5-6 from Shanghai and Xi’an as research subject， and tested their development of patterns. The results show that children aged 5-6 have higher level of repeated patterns but their developmental patterns need to be improved . Children’s understanding of developmental patterns has 4 cognitive levels： pre⁃structure consciousness， confusion of structure consciousness， partial structure consciousness， and structured consciousness. Some suggestions are put forward.

【Keywords】children aged 5-6; repeated pattern; developmental pattern; patterns

*本文为中国教育学会2019年度教育科研重点规划课题“深度学习视域下幼儿园数学与游戏融合共生的行动研究”的研究成果之一，课题编號： 201900652506A。

**通讯作者：田方，博士，陕西师范大学教育学部讲师，E-mail：tianfang@snnu.edu.cn