借图示新视角 促学生深思维
2022-03-11福建莆田市荔城区第一实验小学351100吴荔丹
福建莆田市荔城区第一实验小学(351100) 吴荔丹
数学是严谨、抽象的,而小学生则以直观、形象思维为主,两者之间的矛盾是影响学生学好数学的主要因素。有些数学知识难以理解且复杂抽象,要化解这些抽象难懂的内容,需借助数学图示多元表征(情境图、实物图、示意图、线段图、表格等),将抽象的数学问题生动化、具体化、符号化。那么,如何借助图示教学新视角,为提升学生思维的深度和广度助力?笔者将结合教学实践,从以下三个方面阐述思考。
一、借图识数,理解概念内涵
“数缺形时少直观”,巧用图示可化抽象为直观,再通过分析、综合等思维活动找出共同属性,可凸显概念内涵,展示学生的真问题、真思维,积累真经验、提升真能力。
例如,在教学人教版三年级上册“倍的认识”一课时,经前测分析学生在学习本课之前已具备比较两个量大小的丰富经验。而本课要学习的“倍”是两个量大小的另一种比法,是学生第一次认识倍的概念,但通过二年级的学习,学生已经掌握了乘法中“几个几”的意义。基于以上学情,明确本课的教学重点:结合具体情境让学生理解“倍”的意义,在画图、观察、比较、变式、思辨中经历四个层次的数学建构过程,培养归纳概括和有序、有理表达的能力。
1.第一层次:直观感知,唤醒经验
师(出示图1):将这两个数量进行比较,你会怎么比?(大部分学生想到的是“差比”,即比多、比少)除了比多、比少,还可以怎么说?

图1
生1:○的个数是△的3倍。
(这是学生的前经验,说明对“倍”有一定的认知)
师:同意这位同学观点的请举手。
(大部分学生举手)
师:你是怎么知道○的个数是△的3倍的。
生2:因为6÷2=3,所以它们之间是3倍关系。
生3:我是把2 个△看作1 份,○有这样的3 份,所以它们之间是3倍关系。
2.第二层次:数形结合,理解概念
师:谁能想办法让我们一眼就看出它们的倍数关系?
(生4上前板演,如图2所示)

图2
师:为什么要2个2个地圈画?
生4:因为△有2 个,把2 个△看作1 份,○能圈画出这样的3份,所以○的个数就是△的3倍。
师:在圈画之前,你觉得确定什么很重要?
生(齐):几个为1份。
(学生学会圈画图示后,能用“谁是谁的几倍”表述倍数关系)
3.第三层次:多维变式,深化理解
(1)变比较量
师:如果△个数不变,再加2 个○,现在○的个数是△的几倍?
生(齐):4倍。
师:谁来说说比较的过程。
生5:2 个△为1 份,○有这样的4 份,所以○的个数是△的4倍。
(小结:2 个△看作1 份,○有几个这样的1 份,就是△的几倍)
(2)变标准量
师:回到图1,如果○的个数不变,再加1个△,它们还是3倍的关系吗?
生(齐):不是。
师:是几倍呢?
生6:如图3 所示,△变成3 个为1 份,○可以圈画出这样的2份,所以○的个数是△的2倍。
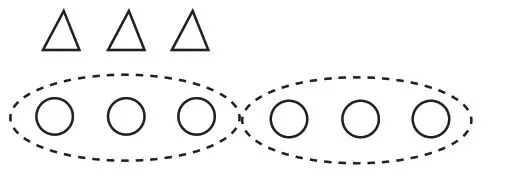
图3
师:为什么要变成3个3个地圈?
生7:之前的○都是与2个△进行比较,现在是与3个△比较。
生8:比的标准量变了,圈画的个数也就变了。
(小结:如果标准量的份数发生了变化,比较量的份数也随之变化,那它们之间的倍数关系也就发生了变化)
(3)倍数不变
师:如果○的个数总是△的2 倍,它们的个数还可能是多少呢?
生9:我先画4 个△,再画8 个○,8 可以分成2个4,所以○是△的2倍。
生10:我先画6 个△,再画12 个○,12 里面有2个6,所以○是△的2倍。
生11:16÷8=2,可以画8个△和16个○。
师:为什么画的○和△的个数不相同,○的个数却都是△的2倍?
(发现:不管1 份的量的个数有几个,只要有这样的几份,就是它的几倍)
4.第四层次:逐步抽象,建构模型
(1)图形抽象
师:如果我们把这样的1 份△用直条表示,○可以用几个这样的直条来表示?
生12:○有这样的2 份,用2 个直条来表示(如图4所示)。
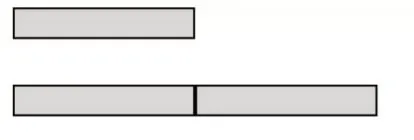
图4
师:如果没有图形和数字,还能看出它们是2倍的关系吗?
生13:可以从直条的长度进行判断。
师:如果给直条“瘦身”,想象一下,会变成什么?
生(齐):线段图。(教师出示图5)
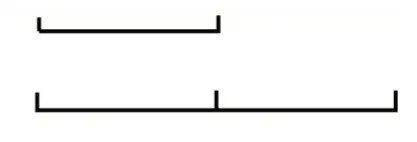
图5
(2)数学抽象
师:如果1 段代表5 朵红花,那2 段表示几朵红花?
生14:1段有5朵,2段有2个5,即10朵红花。
师:有这样的8段,表示有几朵红花?
生(齐):40朵红花。
师:若3段表示18瓶果汁,1段表示几瓶?
生(齐):18÷3=6,表示6瓶。
上述教学中,教师基于学生已有经验和认知基础,准确把握知识本源,精心设计教学活动,引导学生展开深度对话,直指“倍”的概念本质。当学生在数学概念认识上遇到困难时,教师要善于借助图示展开教学,将抽象的“数”转化为直观的“形”,精心设计问题串,让学生依托对“形”的直观表征和可视感知,积累丰富的学习体验,实现有效的数学建构。
二、据图明理,厘清算理本质
计算在小学阶段占比很大。对于以直观认识、直观理解为主的小学生来说,厘清算理是困难的。结合图示教学,让学生借助直观图形来说算理,可使抽象的算理变得具体化。
例如,在教学人教版二年级上册两位数加两位数(进位加)的知识点时,课始出示主题图,呈现学生熟悉的“参观博物馆”情境,引导学生提出“二(1)班和二(3)班一共有多少名学生?”的数学问题,列出算式后,再聚焦35+37 怎么算。解决这个问题的关键在于理解“相同数位对齐”和“满十进1”。
教学时,结合小棒(如图6 所示),学生通过操作将1 根与1 根的小棒对齐、相加,10 根小棒捆成1捆,1捆与1捆的小棒对齐再相加的活动,融合竖式对应理解“相同数位对齐”;通过操作“12 根小棒相加满10 根,把10 根小棒换成1 捆小棒”的过程,理解“个位上满十,向十位进1”。通过呈现小棒图示,架构起“个位与个位对齐,十位与十位对齐”的竖式模型,有效帮助学生厘清“满十进1”的算理。
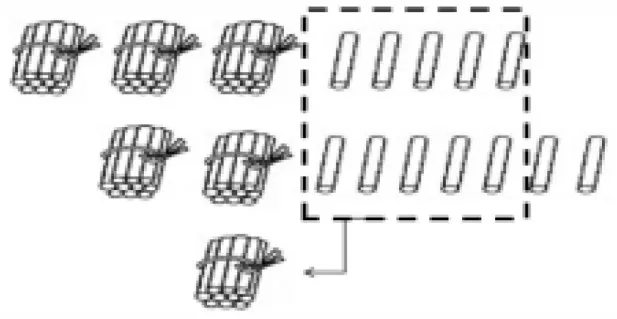
图6
上述教学方法把新知与已有的口算联系在一起进行沟通,学生在理解“个位和个位对齐”的同时,又清楚地掌握竖式计算要从个位加起的计算顺序,建构了“满十进1”算理的数学模型,有效地搭建起算法和算理之间的关系桥梁,实现了“图”与“式”的统一,“理”与“法”的相融。
三、画图促思,提升解题能力
在解决问题教学中,学生经常对一些错综复杂的数量关系不理解。如果在解题过程中,能借用图示这个“脚手架”来帮助学生观察、分析和推理,可便于学生从复杂的信息中抽取出隐性的数学信息,将其转化为显性的数学条件来厘清思路、分析数量关系,进而找到解决问题的策略。
例如,在教学人教版一年级上册认识左右的知识点时,课后出示一道题:一(1)班学生排队,小明的右边有5人,左边有6人,这一队一共有几人?根据低年级学生的年龄特点,通常只能看到题目中的显性条件,很难发现隐性条件。
教师先让学生直接列式,结果很多学生这样列式:5+6=11(人)。接着,教师追问:“这一队有几人呢?为什么?数学是讲道理的。请试一试用画图的方式,把算式的道理表示出来。”学生独立画图后,教师展示学生的说理作品,并引导交流。学生画完图后恍然大悟,并能结合自己画的示意图分析错误原因:原来是漏了加上小明本身。
张丹教授认为,画图是一种解决问题的策略,我们要尊重学生的个性特点,因材施教,鼓励学生画出富有个性的实物图、示意图、线段图、表格等多种多样的形式,因需所画,才能真正有效帮助学生解决问题。上述教学中,教师通过让学生画图,既突破了认识左右的教学难点,又让学生借图思辨,在说理中把易错的知识学得明白,把隐形的道理说得通透,对数学本质的理解也水到渠成,提高了数学思维的深刻性。
又如,解决问题:新区小学五(2)班的图书柜有4 层,其中第3 层和第4 层一共有180 本书,如果从第4 层拿15 本放在第3 层,那么第4 层的本数就是第3 层的第3 层和第4 层原来分别有多少本书?学生根据情境试着自己画出线段图(如图7 所示),根据线段图,有学生很快找到了解题方法:第3 层和第4层一共有180本书、现在第4层的本数是第3层的可以先求第3 层现在有180÷(1+(本),再求第3 层原来有120-15=105(本),最后求第4 层原来有还有学生根据线段图列出方程:把第3层现在的本数设为180,x=120,第3 层原来有120-15=105(本),第4 层原来有也可以把第4 层现在的本数设为第4层原来有60+15=75(本),第3层原来有

图7
由此可见,借助线段图“化数为形”,学生可把文字语言转化为图示语言,通过对比辨析,教师顺思而导,学生一题多解,积累了丰富的解题策略,培养了学生的分析能力和综合能力,实现教师的“教”与学生的“学”的相互切换。
总之,数学图示虽简单,但鲜明、清晰,实用性强。巧用、善用、妙用数学图示进行数学教学,能有效地梳理并构建知识体系,发展学生的直觉思维,发挥图示的教学潜能,促进学生的思维可视化、学习深度化,真正为学生的认知生长形成一片“开阔地”,为能力提升备一部“手扶梯”,为思维拓展构一张“联结图”,有效发展学生的数学核心素养。
