聚焦审辨能力 提升思维品质——以“图形等式”教学为例

浙江杭州市萧山区楼塔镇中心小学（311266） 楼诗音

审辨式思维是21 世纪人才必备的能力之一，它是一个审问、慎思、明辨、决断的过程。《义务教育数学课程标准（2011 年版）》指出：数学教育既要使学生掌握现代生活和学习中所需要的数学知识与技能，更要发挥数学在培养人的思维能力和创新能力方面的不可替代的作用。在小学数学教学中，提升学生的思维能力仍是任重而道远，尤其是提升学生的审辨式思维，更是迫在眉睫且要长期坚持的任务之一。为此，笔者以浙江省张天孝老师编著的《新思维儿童数学》2A 中的“图形等式”这一内容的教学为例，尝试培养学生的审辨式思维能力。

一、教学定位

“图形等式”是在学生已经掌握了平均分、同数连减与除法以及用口诀求商等内容的基础上进行教学的。该课的教学目标为认识图形等式的特点与类型，并通过等式变形求出未知数；通过观察、类比、分析等过程探寻图形等式的内部联系，以此萌发审辨式思维；通过创编、质疑、抽象、对比、概括等过程形成审辨能力。

二、教学实践

创编新题、观察比较、独自思考、交流评价等学习活动，均有益于学生的思维从“浅层思考”迈向“深刻审辨”，是培养学生审辨式思维能力的重要手段。

1.出示等式，审辨等式的意义

师：从3、4、5、6、7、30 中任选三个数组成一个算式。

生1：5×6=30。

师：这个乘法算式还可以改写成怎样的算式？

生2：6×5=30，30÷5=6，30÷6=5。

师：那剩下的三个数呢？

生3：3+4=7，4+3=7，7-3=4，7-4=3。

师：如果任选四个数可以组成怎样的算式？

生4：3+6=4+5，4+6=3+7，5+6=4+7，3×4=5+7，4+7-6=5。

师：像这样含有等号的式子，都叫作等式。

【设计意图：以学生任意选取三或四个数组成等式为引入，引导学生发现数与数之间的关系，形成算术运算。算术运算是学生理解图形参与运算的“拐杖”。在该环节中，介绍等式的概念与等式的变形方法之后，学生可以通过类比来学习相应结构的图形等式推算方法。】

2.等式变形，渗透审辨思维

出示题型一：○+○+○=27 □+□+□+□=24

师：等式的形式有很多，这两个也是等式。想一想，这两个等式跟前面的有什么区别？

师：像这样含有图形的等式，我们把它们叫作图形等式。

师：这些等式中的每个图形分别表示几？请独立完成，再说给同桌听，然后全班交流。

生1：因为三九二十七，所以○=9。

生2：因为○+○+○=27，所以○=27÷3=9。

师“：○+○+○=27”可以变形成什么乘法算式？

生3：○×3=27。

（用同样的方法解决□+□+□+□=24）

师：创编新题后请同桌解决。

【设计意图：该类题为图形等式推算中的基础题型，但已不是具体的算术计算，而是需要分析等式中数与数之间的关系，把算术计算与代数运算相结合，通过等式变形求出未知数，渗透代数思想。

教师不是直接给出同类型的题目让学生熟练解题技能，而是采用创编新题的方法，为学生的学习提供了开放性的学习氛围。新题不是教师提供的，这就为让学生用质疑的眼光来观察提供了前提条件，为培养学生审辩式思维提供平台。】

出示题型二：7×△=26-5

师：这个图形等式与刚才的图形等式有什么相同点和不同点？

生4：它们都是图形等式。

生5：这个等式的左右两边都是式子，而刚才的等式的右边是得数。

师：等号两边分别有怎样的式子，这两个式子的大小关系是怎样的？

生6：左边是“7×△”，右边是“26-5”，它们的大小是一样的，因为用等号连接。

师：请算出△表示几。

生7：因为26-5=21，那么7×△=21，所以△=21÷7=3。

师：创编新题后请同桌解决。

【设计意图：题型一与题型二均为一元一次图形等式，但题型二在题型一的基础上进行了提升，为左右两边均含有式子的图形等式。这类题的解题思路是先对结构进行简化，使其变为只含有一个式子的等式。这联系到解方程中化归的重要思想，是培养学生代数思维的重要训练。】

3.明辨关系，强化审辨思维

出示题型三：

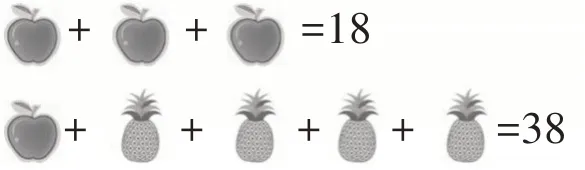
师：观察这组等式，它由几个等式组成？

生1：它由2个等式组成。

师：请想一想我们该从哪个等式入手，为什么？

生2：我认为应该先算第一个等式，因为第二个等式比较复杂。

生3：我也认为应该先算第一个等式，因为第一个等式只有一种图形，而第二个等式有两种图形。

生4：我先算第一个等式，得出苹果代表6，第二个等式中的4个菠萝相加等于38减6得32，一个菠萝就是32除以4得8。

师：根据生4的描述，谁能用算式表示出来？

生5：18÷3=6，38-6=32，32÷4=8。

师：解决这样的题目，你有什么好的建议？

生6：优先解决只有一个不知道的算式。

师：谁能说得更准确一些？

生7：优先解决只有一种图形不知道的算式。

题目变式：

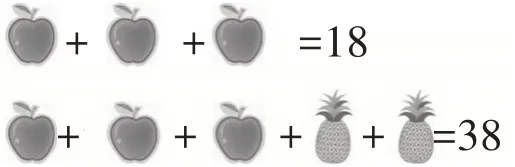
师：现在苹果代表多少？

生8：苹果代表6。

师：为什么题目都变了，苹果还是6呢？

生9：因为第一个算式没变。

师：那菠萝代表多少呢？

生10：38-6-6-6=20，20÷2=10。

生11：38-18=20，20÷2=10。

师：算式“38-18”中的18代表什么，为什么？

生12：18代表3个苹果，我是从第一个算式中知道的。

师：是的，因为这3个苹果与第一个等式的3个苹果是相同的，所以它们可以直接用18来替换。

【设计意图：在该环节中，教师将题目进行了变形，使两个图形等式中均含有3 个苹果，因此学生可以用两种代入方法来求得菠萝所代表的数，即数的代入与式的代入。变形后的题目为下一环节“式的代入”奠定了基础。】

出示题型四：

师：观察这组等式，你有什么发现？

生13：每个等式中都有两种图形。

师：那么能用刚才的方法算出图形分别表示几吗？

生14：不能。

师：谁来解这道题？

生15：我们从第二个等式中可以知道2 朵红花和2 朵蓝花代表22，所以第一个等式中的2 朵红花和2 朵蓝花也是22，而22+15=37，所以3 朵蓝花是15，那么1 朵蓝花就是5。接着算出2 朵红花是22-5-5=12，所以1朵红花是6。

师：谁听明白了？

生16：这两个算式是有相同部分的，可以用22替换，而22+15=37，所以3 朵蓝花是15，1 朵蓝花是5，再把所有的蓝花换成5，就可以算出红花是6。

师：听明白这两位同学的意思了吗？当两个等式都不能直接解决的时候，怎么办？

生17：找出两个等式相同的部分。

师：是的。在这道题中，我们发现两个图形等式都有两种图形，也就是都不能直接解决。可以先观察这两个等式是否有相同的地方，再进行替换，从而简化等式，解决问题。

【设计意图：当两个等式中均含有两个未知图形时，应先分析、明辨式与式的关系，将一个式子整体代入，从而得到更简单的表达式，这是代入的方法；另一种方法是将两个等式进行比较后进行加减。代入法与加减法是互相联系、不可分割的。

在教师展示的三组图形等式组中，虽都以前一组的解题方法为依托，但需代入的“整体”从单个量、多个相同的量，逐步过渡到多个不同的量。这样的过程使学生在解题时不能简单照搬前一组的方法，而是先对前一题的方法进行批判与明辨，学生进行了主动的学习性探究，同时也开启了审辨式思维的大门。】

4.课堂总结，回顾课堂所学

师：今天这节课我们主要学习了什么内容？在这些图形等式中，有些只有一种图形，可以直接解决，而一些有两种图形，这就需要用你们的“火眼金睛”，找到已经知道的或者可以替换的部分后再解决问题。

【设计意图：教师总结是对整节课中的图形等式进行分类整理，也是对不同类别的图形等式的推算方法进行回顾和总结。】

三、教学反思

1.以创编新题为活动，发展审辨式思维的“审问”能力

在一元一次图形等式的教学中，笔者分别让学生对不同题型进行创编。新题的创编是需要建立在学生已形成结构意识的基础上，说明学生已把该环节所学知识内化成了自己的知识。第一个学生创编新题后，第二个学生在解答前必须检验所编新题是否符合该类题型的要求，继而认真解答该题。这其实也是经历了对对方形成“审问”的过程。因此，创编新题能发展学生审辨式思维的审问能力。

2.以问题串引质疑，激活审辨式思维的“慎思”能力

在教学“7×△=26-5”的环节中，教师以问题串的方式不断提问学生：这个图形等式与刚才的图形等式有什么相同点和不同点？等式中有哪两个式子？两个式子的大小关系是怎么样的，为什么？它们的得数都是多少，为什么？这是一个师生不断互动的过程，学生从问答中思考解题过程的每一步依据的理由，从而获取解题方法，并激活了审辨式思维的慎思能力。

3.以两式异同作比较，提升审辨式思维的“明辨”能力

在该课教学中，教师多次采取两式比较的方法，使学生明辨两式的异同，从而发现解题方法。例如，比较题型一与题型二的区别，得出题型二的等式中含有两个式子，可先解决其中一个式子的得数，以简化等式；比较题型三变式中的两个等式，明辨其关系——两个图形等式中均含有3 个苹果，因此可以用两种代入方法来求得菠萝所代表的数，即数的代入与式的代入；比较题型四中的两个等式，分析、明辨式与式的关系，学习将一个式子整体代入，从而换取更简单的表达式，也可将两个等式进行比较后再加减。在不断比较、分析、思考的过程中，学生的审辩式思维得到发展。

4.以图形等式组为媒介，强化审辩式思维的“决断”能力

二元一次图形等式推算是以一元一次图形等式的推算方法为基础的，是对一元一次图形等式推算方法的应用。而与一元一次图形等式的推算不同的是，二元一次图形等式推算的复杂程度取决于式与式的关系清晰程度。学生的学习主要从数的代入开始，即先从选定等式中求出一个未知数的值，再让它参与到另一个等式的运算中，以求得未知数。这都需要学生学会分析并选定等式组中可以优先解决的等式。在这样的过程中，学生的分析与决断能力得到培养，审辩式思维得到充分地刺激与强化。