非线性声波方程的几种解法对比

张世功，丁 凯，张克声，苏向东

(1. 贵州理工学院，贵州 贵阳 550003；2. 贵州省医工交叉工程研究中心，贵州 贵阳 550003；3. 近地面探测技术重点实验室，江苏 无锡 214035)

0 引 言

测量介质的非线性系数在医学诊疗和材料的无损检测上都有至关重要的作用。生物组织的声阻抗在发生病变时会产生微小的力学性能变化，通过表征材料非线性系数可以找到不易(被线性超声)发现的病变组织(诊断成像)并进行后续治疗[1-2]。而在固体介质中，利用传统的无损检测手段很难发现微裂纹、热损伤、应力集中等早期危害。而表征非线性系数可及时发现这些早期损伤，对其干预可以减小服役过程可能会带来的损失[3-5]。

众所周知，大多非线性问题理论上难以解决，常用的摄动理论只是一种近似方法。利用它围绕非线性系数对非线性声波方程进行摄动展开，能得到一系列解。原则上，所有阶次解之和才是非线性声波方程的解析解，但要得到高阶次的摄动解非常困难，而低阶次的近似摄动解的误差较大，适用范围也相对有限。数值仿真计算，比如有限元、有限差分等方法[6-7]也可以用来计算非线性方程。然而，数值解得到的都是数值，不易用来分析相关的物理规律。另外，非线性声学中会引起高次谐波的产生，有限的空间步长和时间步长能造成计算时的发散问题。

目前，实验表征材料非线性系数时常用二阶摄动解进行计算[5,8-9]，但二阶摄动近似解只能在近场或小振幅激励信号才适用，当样品不太小或激励源不太弱时，得到的实验结果会有较大误差[9]。

在介绍气、液、固三种状态介质中非线性声波方程的基础上，本文阐述了多种求解一维非线性声波方程的方法。首先，通过理论分析，三种状态中的非线性声波方程具有相似的形式，这表明不同状态下的非线性声波应有相似的传播性质。其次，利用符号计算工具可获得8阶摄动解，并与有限元、有限差分两种数值解比较，将得到的非线性声波时域波形与实验进行了对比。再次，通过比对线性方程和非线性方程的形式，采用线性方程的求解方法对非线性声波方程求解，得到非线性方程的伪线性解。上述多种解得到的时域波形都显示了波形畸变等非线性声波的传播性质。为证实这些解的非线性传播性质，在水中开展非线性声场的测量实验，验证了这些解的有效性。高阶摄动解能用来更精确地测量介质的非线性系数。当然，非线性声波方程的多种解法也可为非线性声学的其他相关深入研究提供理论依据。

1 气液固介质中的非线性声波方程

固体中的非线性包括材料非线性和几何非线性[10-11]。材料非线性源自原子的不规则排列，主要表现为应力和应变的非线性关系。而几何非线性（也称非经典非线性[12]）主要考虑的是大的几何变形引起的非线性问题。本文主要讨论的是材料非线性问题。

利用应变能公式[13-14]可以得到各向同性固体介质中的一维非线性声波方程[15]：

流体中的非线性声波传播问题研究过程要更复杂一些，Earnshaw等发展了初期的非线性声传播理论[17-20]，Fubini, Fay, Blackstock等对拉氏坐标下的非线性声波方程组式(2)进行求解。

其中：ρ和ρ0，p和p0分别为有扰动和无扰动情况下的介质密度和压强。通过求解获得了相关条件下的解析解。Beyer则改写(2)式，得到了气、液体中的非线性声波方程[18]：

式中：γ是气体的比热容比；B/A为液体的非线性参数，与Landau描述固体介质非线性性质的A、B无关。设是流体中的非线性系数[19]。利用泰勒展开，可将式(3)、(4)改写为

比较式(1)和式(5)，可以发现，气液固三种介质中的非线性声波方程形式上完全一样，只是固体中的非线性系数β是流体中非线性系数的–2 倍[6,9](文献[19]中非线性参数B/A为5，对应=–3.5)。这也是一些文献中二阶摄动近似解的常系数是1/8[9]，然而另一些文献中是1/4的原因[1,5]。

2 一维非线性声波方程的五种解法

2.1 经典解析解[19-20]

Fubini, Fay等对流体中的非线性声波方程(2)求解，分别得到近距离和远距离的相对振速解：

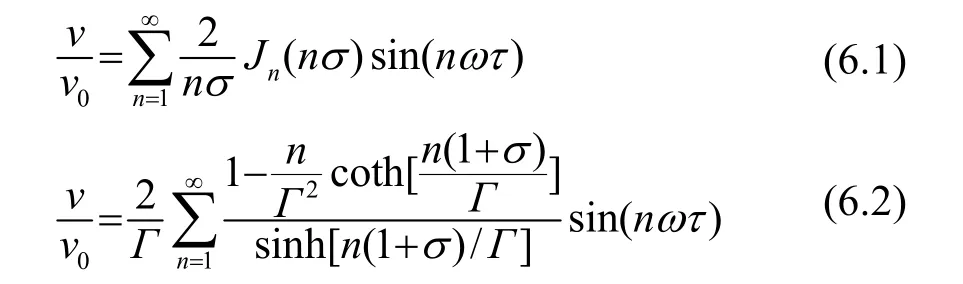
式中：v和v0分别为谐波和激励信号的质点振动速度，即v/ v0表示谐波的相对(激励信号)振动速度。但式(6)无法在冲击波产生位置附近取得较好的结果，Blackstock利用桥函数：

将式(6)桥接起来，相对完满地解决了问题。式(6)在许多文献中均有详细阐述，因此不再过多展开说明。

2.2 摄动方法

式(7)被称为非线性声波方程的高阶摄动展开方程，一阶摄动展开方程(7.1)的解为。其他方程均为非齐次方程，非齐次项由低阶次谐波组成，即低阶谐波可以认为是高阶谐波的源。低阶(如i和j)次谐波耦合形成和(i+j)谐波，也可合成为差谐(i–j)波。

高次谐波解的形式会随着摄动展开阶次的增加变得越来越复杂，为了得到n阶的高次谐波解，所有比n小的谐波都需要已知。

利用符号计算工具，并进行简单的人为干预，可以得到高达8阶的非齐次方程特解：

式(8)中： θ =ωt- k x ，因更高阶的谐波解过于复杂，只将偶数次谐波里的二次谐波列出，参见附录。从式(8)中可以看出，所有偶数阶次的谐波解中均包含二次谐波解。理论上分析可知，得到高次摄动解的阶次越高，二次谐波的最终表达式会越接近真实解。非线性声波方程(1)的解析解应该是所有摄动展开方程的解之和。

2.3 有限差分方法

一维非线性声波方程式(1)的差分形式可以表示为

这里不会产生横波，求解过程相对横波激励的非线性声波[21]更加容易，此处不再详述计算细节，但需要注意的是它的空间和时间步长不能采用通常差分方程中的步长。为适应高次谐波的短波长，计算采用的空间和时间步长要远远小于1/8的波长和周期。文中采用了1/160波长的空间步长。另外，非线性声波方程的边界条件问题也较为复杂，可采用相对较长的介质，若只研究声波反射之前的传播性质，边界条件问题就可以不作考虑。

2.4 有限元方法[6]

利用有限元方法，方程(1)可写为

其中：M、K、B、F分别表示质量矩阵、刚度矩阵、非线性刚度矩阵和力源，其他相关参数的物理意义参见前期的研究工作[6]。

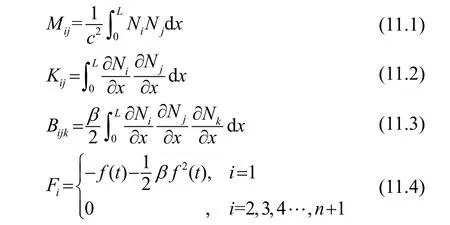
通过计算可以得到非线性声波方程的有限元数值声场。

2.5 伪线性解

即不同位置(或位移空间梯度)处的质点具有不同的声传播速度，这样，非线性声波方程的解可化简为

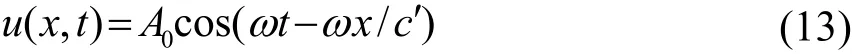
式(13)即为非线性声波方程的伪线性解，但它不能直接获得，仍需要部分数值计算。在计算下一时刻的声场时，将当前时刻下的每个位置的声速利用式(12)进行估计，代入(13)即可计算下个时刻的声波时域波形。

3 理论计算与实验结果的对比

为验证上述解的正确性，同时为了测量不同位置的非线性声场的便利性，在水中开展非线性声学实验，实验在Ritek-SNAP-5000系统上开展。信号发生器发射 12个周期的脉冲射频信号给功率放大器放大后再传给水中主频为2 MHz的超声换能器，换能器将电信号转化为超声信号在水中传播，并由水中另一个宽带超声换能器接收后再传入系统进行分析与存储。水的密度为1 g·cm-3, 声速经测量为1491 m·s-1。取文献[19]中= -3.5或 β=7进行数值计算。

有限差分数值解(Finite Difference Time Domain, FDTD)和伪线性解(Pseudo Linear Solution,PSEU)的时域波形与实验信号(Experimental Signal,EXP)的对比如图 1所示，这些信号均是在距离声源 6 cm处得到的。理论的伪线性解为无限长的稳态解，图中的波形是用了梯形窗进行时域上截断的结果。

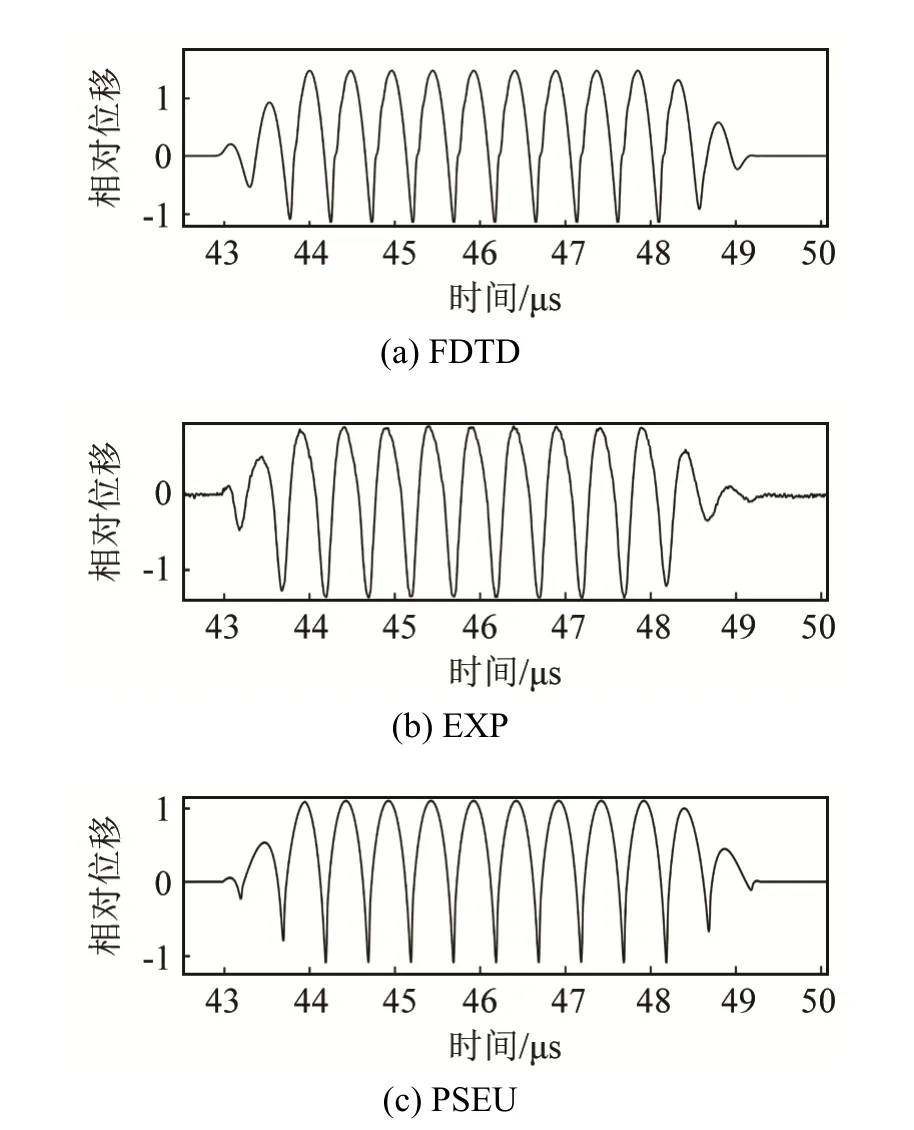
图1 有限差分法和伪线性解得到的距声源6 cm处非线性声波位移信号与实验结果比较Fig.1 Comparison of the nonlinear ultrasonic displacement signals at 6 cm from source obtained by FDTD, PSEU and EXP

Blackstock桥函数提供了不同传播位置的(相对声源的)相对振速解(或归一化解)，但是通过式(6.3)并不能得到时域波形信号；同时，仅利用8阶次的谐波(包括基频)信号，得到的摄动时域波形与实验信号相差仍然较大；而通过有限元方法计算的时域波形与有限差分的结果几乎完全重叠。这三种结果均未在图1中列出。

有限差分(或有限元)及伪线性解的时域信号均与实验信号相似，都能展现非线性声波信号的波形畸变性质。正弦波随传播距离逐渐演化为尖锐的三角波。通过对时间求导，也可以得到如图2所示的质点振速的锯齿波。

图2 有限差分法和伪线性解得到的距声源6 cm处非线性声波质点振速信号与实验结果比较Fig.2 Comparison of the nonlinear particle velocity signals at 6 cm from source obtained by FDTD, PSEU and EXP

根据式(8)，谐波幅度随传播距离增加而增大，即非线性声波的畸变程度会加剧，如图3所示。实线从下向上为 2、4、6 cm 处接收的非线性声波，而虚线为对应位置的FDTD计算信号。显然，实验和理论计算的仿真信号正如式(8)预期，畸变程度逐渐变大。非线性声波波前将最终演化为冲击波。

图3 有限差分法得到的距离声源2、4、6 cm处接收的非线性超声信号与实验结果比较Fig.3 Comparison of the nonlinear ultrasonic waves measured at 2, 4, 6 cm from source obtained by FDTD and EXP

利用信号处理可得到不同声传播距离下的基频信号和二次谐波相对(位移)幅度，如图 4所示。EXP表示实验信号，P2、P4、P6、P8为相应阶次的高阶摄动解(Perturbation, PERT)，FIT (Fitting Solution)代表前期工作中的拟合解[6]，FDM为对有限差分信号的处理结果，PSEU为伪线性解，BLKS为Blackstock桥函数的解。需要说明的是，图4中是位移的相对幅度，对于二次谐波，考虑线性解和式(8.1)，其值为，而文献[18, 20]中振速的相对幅度为，它们之间存在两倍的差异[6,18-19]。

基频信号的相对位移幅度位于图4中的上方位置，在接近声源位置时，因为尚未有随传播距离积累的谐波出现，即基频信号还未向高次谐波转化，同时也无损耗、扩散衰减发生，相对幅度从1开始随传播距离减小，标志着基频信号随传播距离开始向谐波传递能量。在远离声源位置处，考虑到扩散衰减和吸收衰减，实验信号在所有理论计算结果中的相对幅度最小。

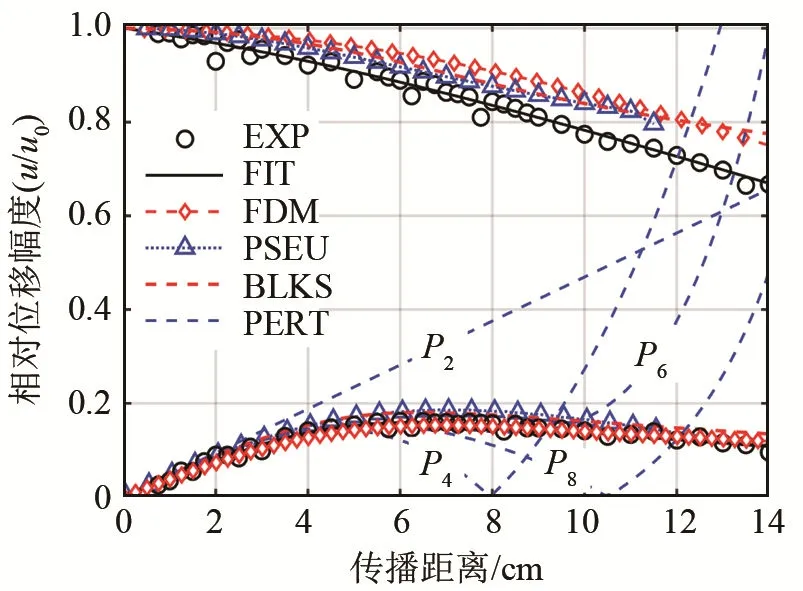
图4 不同方法计算和实验得到的不同传播位置的基频(上)和二次谐波(下)相对(声源)位移幅度Fig.4 Relative displacement amplitudes of fundamental(upper) and second harmonic (lower) at different propagation distances obtained by different calculation methods and experiment

二次谐波的相对幅度位于图4下方，同样由于传播距离和衰减的原因，其相对幅度从 0开始增加，增加到一定幅度后逐渐减小，实验的二次谐波相对幅度在远距离处也同样比几种理论计算值小。

4 讨 论

对于摄动法，其一阶摄动展开方程的解为线性方程的解，信号的振幅为常数，相对幅度一直为1。而在3阶、5阶、7阶等奇数阶次摄动展开方程的解中均有一次波出现，比如三次谐波摄动展开方程式(7.3)中，二次谐波和一次耦合成三次的同时，还能耦合出一次谐波(见式(8.2))。文中称高次摄动展开方程得到的一次波为一次谐波。偶数次谐波解中不包含一次波。将所有摄动展开方程的一次波叠加，才能得到基频信号随传播距离的变化规律。

对于二次谐波，P2为只考虑二次谐波的摄动解，它与传播距离成线性关系，仅能在较接近声源时才与实验结果吻合。而P4、P6、P8为分别考虑了对应的高次谐波中的二次谐波成分(所有偶数阶的摄动展开方程中均能耦合二次谐波)，能在更宽泛的测量条件下比低阶近似解更贴近实验结果。但图中P8相对P6似乎并未提高精度，这在数学上也能够理解，因为将所有阶次的摄动解累加起来是非线性声波方程的解，而这里讨论的只是二次谐波。但总体上考虑的阶次越高，这些解越能接近实验结果。

摄动解(也包括其他解)在传播距离较远时与实验结果的差异仍相对比较明显，一方面是由于在远距离处应考虑更多高阶的谐波解，另一方面，远距离处的吸收衰减和扩散也不能忽略。另外，源信号的形状也需要考虑，摄动解(和伪线性解)是连续波，而实验与数值计算中采用的是脉冲串。同时，文中未涉及更高阶次的材料非线性系数，这些也会对结果造成一定影响，其他相关文献中[9]也有类似的实验结果，呈现了非线性问题的复杂性。

就二次谐波的相对幅度而言，几种理论解的精度在测量的距离范围内均相对较为理想，与实验结果的吻合程度也较高，这是因为文章考虑的是介质非线性，谐波随传播距离产生并与其他阶次的谐波(也包括一次波)相互耦合，最终形成与声波幅度、传播距离等许多物理参量相关的极为复杂的数学关系。在传播距离不是非常远的情况下，这些解具有一定的精度，但在传播距离较远时，这些解之间以及它们与实验值之间的误差仍需要进一步的研究和分析。

文中介绍的五种非线性声波方程解法之中，有限元和有限差分都是数值解，摄动方法是一种近似的解析解，虽然伪线性解是形式上的解析解，但只能写出一种隐函数式，波形计算需要一定程度的数值计算。Blackstock桥函数能描述不同传播距离下所有高次谐波的质点相对振速幅度，然而并不能得到传播过程中波形的变化趋势。

摄动解限制于能求解出的阶次，尽管已经得到了高达八阶的谐波解，但合成的非线性时域波形的畸变程度仍远远不够。但它的优点也是其他方法不具有的，即定量分析。许多实验仍运用二阶摄动近似解(式(8.1))表征介质的非线性系数[5,8-9]，但这不能在传播距离较远(或介质较长)和激励信号幅度较高时的情况下与实验结果取得较好的一致性[9]。非线性声波的传播距离越远，谐波就越复杂，更高阶谐波解中的二次谐波的成分不能被二阶摄动近似解囊括，它的局限性就越能暴露出来。显然，文中的8阶非摄动解已能大大扩展非线性系数实验的测量范围，当然也能提高其测量精度。

有限差分和有限元方法在意义上略有不同，然而它们的结果几乎一致，直观观察时域声场的演化过程比较容易，传播性质也可通过信号处理较容易地得到，但却不利于量化分析。伪线性解实际是一种半解析方法，在它的非线性解中，声传播速度随时间和传播位置(或质点振速的空间梯度)的变化而变化。

5 结 论

文中介绍了求解一维非线性声波方程的五种方法，比较分析了它们的优劣和适用范围。有限差分法和有限元方法均能直观地观察时域波形随传播距离的演化过程。而伪线性解和摄动法得到的是无限长的稳态解，Blackstock桥函数不能得到时域波形。

在分析高次谐波相对幅度随传播距离(或激励信号幅度)的传播性质上，除摄动解外，其他四种方法的计算结果都与实验结果有较好的一致性。然而，由于摄动解被广泛应用在非线性系数的定量计算上，二阶摄动近似解仅在接近声源的区域内适用性高，更高阶次谐波摄动解中的二次谐波可扩展非线性系数表征的测量范围，同时也能提高它的测量精度。

与实验结果的对比验证了几种非线性声波方程解的有效性，预期可为测量流体和固体介质非线性系数提供更精确的方法。

附录