基于电磁超声的塑性损伤铝材抗拉强度预测
2022-03-11刘素贞崔子妍
刘素贞,崔子妍,张 闯,金 亮
(1. 省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津 300130;2. 河北省电磁场与电器可靠性重点实验室(河北工业大学),天津 300130)
0 引 言
铝合金板材在外部载荷作用下会发生塑性变形,塑性变形会降低金属的抗拉强度并影响结构的安全使用[1]。电磁超声多用于含有微观损伤材料的安全检测[2],因为超声信号对微观损伤敏感[3],其利用声波传播过程中与损伤相互作用产生畸变来表征损伤[4],进一步预测材料强度;并且检测过程中无需换能器和被测物体间的耦合介质,可以更加便捷地进行检测[5-6]。
Pfeifer等[7]使用瑞利波检测不同X52钢制成的试件中的塑性应变,使用相对非线性系数表征塑性应变在试件中的积累。谷涛等[8]利用一定频率内非线性参数的累积效应来表征金属蠕变程度,通过该方法对P91钢管道蠕变损伤程度进行了检测。Men等[9]采用临界折射纵波测量了不同热处理的钢试件的波传播时间,计算了不同试件传播波速的不同,建立了一种使用临界折射纵波评估钢抗拉强度的模型。张闯等[10]检测了不同塑性损伤铝合金试件的超声二次谐波幅值,并计算其相对非线性系数,发现相对非线性系数与声波的传播距离之间存在线性关系,即随着波传播距离的增大,相应的二次谐波幅值呈线性增大。Lee等[11]利用超声波的波速表征不同固化方法的混凝土的强度,提出了一种指数函数预测模型来对强度变化进行建模。Kang等[12]针对电磁超声换能器(Electromagnetic Acoustic Transducer, EMAT)换能效率低这一缺点,提出当磁体的宽度比EMAT线圈的宽度窄时,瑞利波的振幅达到最高水平。
在实际检测塑性损伤试件的过程中,电磁超声接收信号的信噪比低会在很大程度上影响检测的准确性[13]。在检测损伤时,携带不同损伤的试件其应力状态也不同[14],所以在进行塑性损伤试件的抗拉强度分析及预测时有必要加入试件内部应力的分析来提高预测的可靠性。国内外学者利用应力三轴度来表征试件应力状态,进一步研究试件力学性能[15]。Schmidt等[16]通过比对不同应力三轴度范围的试件实验,提出在负应力三轴度状态下的相关断裂应变临界值。Lin等[17]通过在不同温度条件下进行铝合金的拉伸实验,得到了其断裂应变随应力三轴度和温度的综合变化规律。Zhang等[18]通过有限元计算对取决于应力三轴度的材料抗拉强度进行了实验分析,确定相应的临界载荷,对不同裂纹尺寸的三维试样进行了弹塑性计算,提出了抗拉强度与应力三轴度之间的一种定量关系。Wang等[19]分析了不同应力三轴度的Ti6Al4V试件的断裂行为和断口机理,发现较高的应力三轴度或应变率促进了材料的脆化,使材料的抗拉强度变低。
目前,对金属塑性损伤的检测大多数只是对超声检测信号的分析,受接收信号不稳定的影响,导致了检测结果精确度不高。本文利用应力三轴度表征不同塑性损伤试件内部的应力状态,并对不同塑性损伤试件进行电磁超声检测,通过相对非线性系数完成对试件塑性损伤的表征。由于相对非线性系数和应力三轴度这两个参量随塑性损伤变化趋势不同,使得这两个参量敏感的损伤阶段不同,综合分析试件抗拉强度-应力三轴度和抗拉强度-相对非线性系数之间的关系,形成相对非线性系数-应力三轴度的复合预测方法,以期更好地预测材料的抗拉强度。
1 含塑性损伤试件应力分析及电磁超声检测基本理论
1.1 应力状态的表征
为了表征材料拉伸过程中的应力状态,引入应力三轴度η这一参量,定义为[20]

式中:σv为试件内部平均应力,σe为试件内部等效应力,这一比值反映了材料在三轴应力场中产生塑性应变时受到的约束程度。对于金属材料,等效应力用于反映试件内部的塑性变形,平均应力反映试件内部的弹性变形,这两个量的比值应力三轴度考虑了两方面的因素,合理地体现出了不同应力分量对塑性应变的影响[20]。在三维有限元计算中由三个主应力σ1、σ2、σ3来计算应力三轴度[20]:

材料拉伸断裂过程中,考虑到应变历史的积分形式可以表示为

1.2 非线性电磁超声表面波波动理论
利用电磁超声换能器(EMAT)激发表面波时,当高频电流被通入线圈后,会在被测试样表面产生感应涡流,在偏置静磁场作用下产生洛伦兹力,洛伦兹力使试件产生周期性的振动,以波的形式进行传播。试件内部存在塑性损伤时,会使得被激发出的表面波畸变,从而产生以二次谐波为主的高次谐波,非线性超声波动方程可表示为[22]

式中:A0为超声波的初始幅值;k为波数。
引入二次谐波幅值,可得到材料的二阶非线性系数:

式中: A1为基波幅值;A2为二次谐波幅值;β为二阶非线性系数。由于实验中发射的超声波频率和被测试件长度保持不变,所以二阶非线性系数可以简化为

在试件塑性损伤检测中,通过检测接收信号的二次谐波幅值来表征试件内部由于损伤引起的非线性。
2 铝板塑性损伤电磁超声表面波三维模型的建立与分析
2.1 铝板塑性损伤三维模型的建立
本文以 6061铝合金为研究对象,参照国家标准设计试件。试件长度为280 mm、宽度为70 mm、厚度为 10 mm、平行长为度 150 mm、原始标距为113 mm。按照实际设计的铝板尺寸进行仿真建模,如图1所示。使用COMSOL Multiphysics有限元软件对铝合金试件单轴拉伸产生塑性损伤进行仿真计算,在材料属性中添加弹塑性属性。边界条件为设置一定拉伸距离的指定位移,对拉伸距离进行参数化扫描,从而改变材料内部塑性应变大小,以表征不同程度的塑性损伤。图2为仿真拉伸过程中各个阶段试件内部塑性应变分布图。
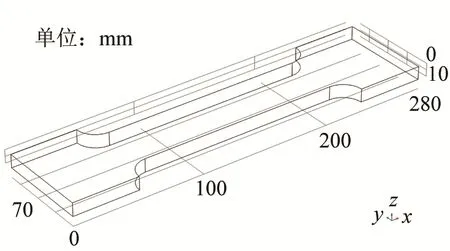
图1 铝板塑性损伤仿真模型Fig.1 Simulation model of plastic damaged aluminum plate
如图2所示,通过对铝合金试件拉伸过程仿真可以看出试件内部塑性应变的变化情况。当试件处于拉伸弹性阶段,材料内部变形均为可逆的弹性形变,塑性应变几乎为 0。在材料的屈服硬化阶段,随着材料应变量的增加,应力也持续增加,材料出现较为明显的伸长。仿真过程以1%应变为步长、依次增加至10%,整个过程应力应变曲线如图3所示。

图2 塑性应变分布图Fig.2 The distribution of plastic strain

图3 应力-应变曲线图Fig.3 Stress-strain curve
由图3可知,在应变ε<4 %时,试件处于弹性阶段,应力-应变关系呈线性。当应力达到150 MPa附近时,试件进入屈服硬化阶段前期(4%≤ε<6 %),应力增长变缓,试件中部开始出现小范围应力集中现象。当6%≤ε<8%时,铝合金试件处于屈服硬化后期,随着应变的增大,材料长度明显增大。此时内部应力持续增加,材料伸长量明显增大。当应变增加到8.5%左右时,试件接近颈缩状态,随着应变增大,应力开始逐渐降低。
在三维仿真中计算试件的σ1、σ2、σ3,进而计算应力三轴度。选择试件最小横截面的中心点,即应力集中程度最高点计算,与二维仿真模型相比,三维模型考虑z轴方向上的力,使得计算结果更加贴合实际。得到应力三轴度随应变变化的曲线如图4所示。

图4 应力三轴度-应变曲线图Fig.4 Stress triaxiality-strain curve
由图4可以看出,随着试件内部塑性应变的增大,其应力三轴度也增大,并且在屈服硬化阶段后期(6%≤ε< 8%),应力三轴度的增幅明显变大。这是因为在拉伸前期,铝板没有明显的应力集中,随着板内塑性应变的增加,局部横截面变小,应力三轴度也开始上升且上升幅度较大;而后趋于稳定,增幅变缓。
在试件产生塑性损伤阶段,均匀取试件编号为A1~A5的5个试件的应变值作为研究点,其应力三轴度如表1所示。
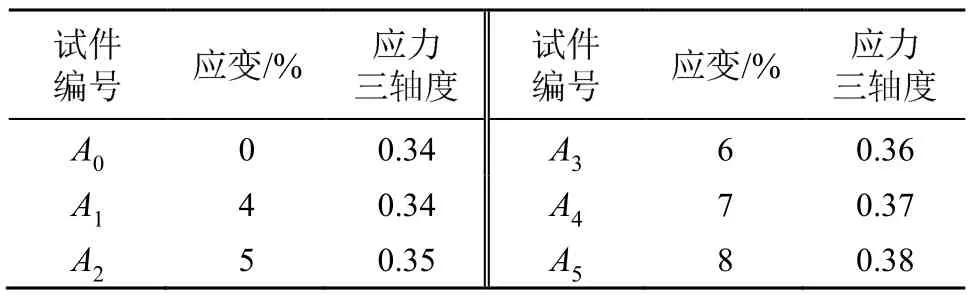
表1 不同试件的应力三轴度Table 1 Stress triaxiality of different specimens
2.2 电磁超声换能器仿真模型的建立
对塑性损伤试件电磁超声检测系统进行三维仿真建模,使用COMSOL Multiphysics仿真软件对电磁超声表面波检测过程进行建模分析,涉及磁场和固体力学场的计算。除了铝板的上下两个端面,其余端面设置为低反射界面。激发线圈频率为1.6 MHz,表面波长λ=1.82 mm,相邻曲折线圈间距d=λ/ 2 。曲折线圈中通入幅值为30 A的激励电流信号。在稳态求解器中计算偏置磁场和铝板中由于拉伸产生的塑性变形,在动态求解器中计算通有高频交流电的线圈产生的动态磁场,仿真模型如图5所示。
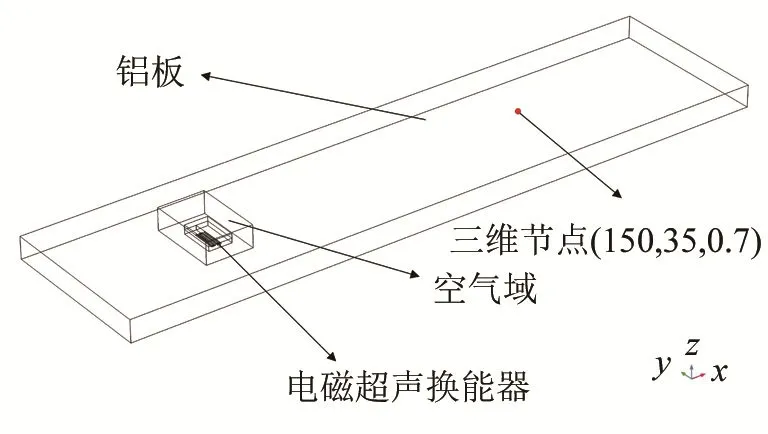
图5 三维电磁超声仿真模型Fig.5 The three-dimensional simulation model of electromagnetic ultrasound
取三维节点(150,35,0.7)作为检测点,从频域进行质点位移的分析,图6为应变ε= 6 %、ε=7%、ε= 8 %时在三维节点处的接收波形图。
从图6可以看出,三维节点处的接收信号在频率为3.2 MHz处产生二倍频信号,进一步分析可发现不同塑性应变使得接收点处接收到的信号中二次谐波幅值不同,随着应变的增大(6%、7%、8%),二次谐波幅值随之增大(0.019 V、0.023 V、0.025 V)。不同塑性应变下的相对非线性系数如图7所示。


图6 不同应变下的接收信号频域波形图Fig.6 Frequency domain waveforms of received signals under different strains
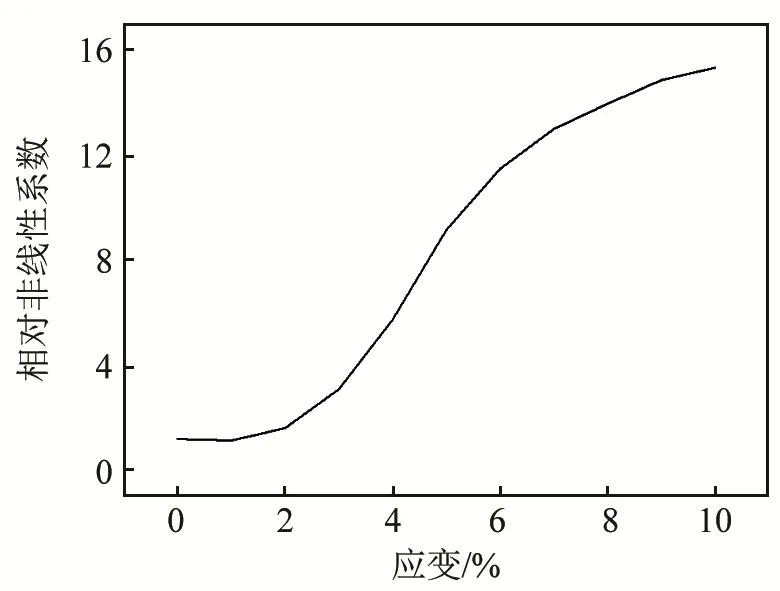
图7 不同应变下的相对非线性系数Fig.7 The curve of relative nonlinear coefficient versus strains
由图7可知,当试件处于屈服硬化阶段的前期(4%≤ε<6%)时,相对非线性系数增长较快,在屈服硬化阶段后期(6%≤ε< 8 %)增长趋于平缓。通过对比相对非线性系数随塑性应变的变化规律和应力三轴度随塑性应变的变化规律可以看出,相对非线性系数在屈服硬化阶段前期(4%≤ε<6%)增幅较大,而应力三轴度在屈服硬化后期(6%≤ε< 8 %)增幅较大,这两个特征参量对损伤敏感的时期不同。所以可以根据试件的塑性应变来选用不同特征参数表征损伤。
在试件产生塑性损伤阶段,均匀取试件编号为A1~A5的5个试件的应变值作为研究点,其相对非线性系数如表2所示。
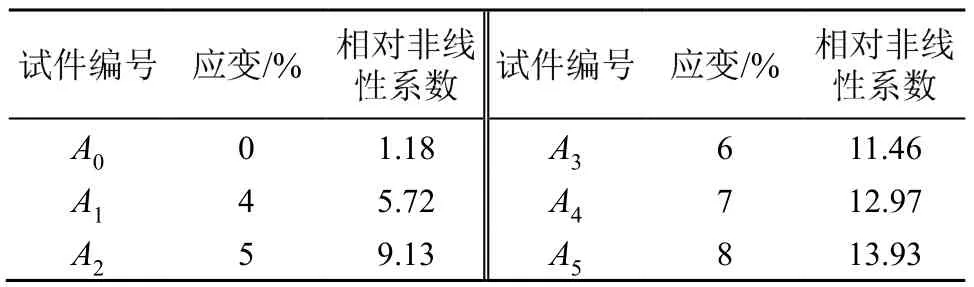
表2 不同试件的相对非线性系数Table 2 Relative nonlinear coefficients of different specimens
3 塑性损伤试件的电磁超声检测实验
3.1 非线性电磁超声检测实验
在室温条件下,对图1中的铝合金试件进行单轴拉伸,实验设备采用电子万能试验机。将其中一个完好铝板拉断,得到其应力应变曲线如图8所示。

图8 应力-应变曲线Fig.8 The curve of stress versus strain
所有试件均为相同底材、同一批次加工定制得到,在实验前为确保完好试件的状态一致,对5个试件进行电磁超声非线性检测,测得其相对非线性系数都处于较低的水平。接着把试件分别拉伸至应变为4%、5%、6%、7%、8%,使其出现不同程度的塑性损伤,将试件卸下后进行电磁超声检测。
非线性电磁超声检测系统包括示波器、非线性高能超声测试仪器(Ritec-SNAP-5000)系统、激发端EMAT、接收端压电换能器和被测试件,激发线圈频率为1.6 MHz,实验平台如图9所示。

图9 非线性电磁超声检测实验系统Fig.9 Experimental system for non-linear electromagnetic ultrasonic testing
将拉伸至一定塑性应变的 5个试件A1~A5依次进行电磁超声非线性检测,使每个塑性损伤试件的检测位置保持一致,每个试件进行三次检测,记录结果并取平均值。对时域信号波形进行频域变换并提取基波和二次谐波幅值,根据基波和二次谐波幅值计算相对非线性系数,研究其随塑性应变的变化规律,具体结果如图10所示。
从图 10中可以看出,相对非线性系数和塑性应变关系成正比,在屈服硬化阶段的前期相对非线性系数增长较快,在屈服硬化阶段后期增长趋于平缓,与仿真结果一致。
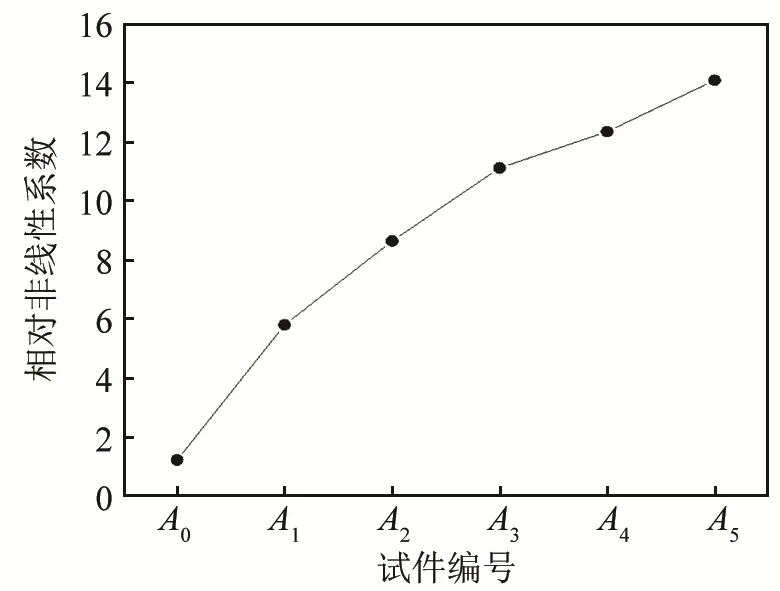
图10 不同试件的相对非线性系数Fig.10 Relative nonlinear coefficients of different specimens
3.2 不同塑性损伤试件的抗拉强度分析与预测
使用电子万能试验机将A0~A5这6个含有不同塑性损伤的试件分别进行拉伸实验,拉伸至断裂测得其抗拉强度,并对数据用函数y=a-bcx进行拟合得到抗拉强度-应力三轴度拟合曲线,结果如图 11所示。

图11 抗拉强度-应力三轴度拟合曲线Fig.11 Fitting curve of tensile strength versus stress triaxiality
由图 11可以看出,随着应力三轴度增大,试件的抗拉强度降低,这是由于随着试件塑性损伤的增大,试件内部应力集中变大,其应力三轴度也相应变大,而应力集中越明显试件的抗拉强度就会降低。采用函数y=a-bcx进行拟合,得到抗拉强度-应力三轴度拟合函数,并进行化简得到:
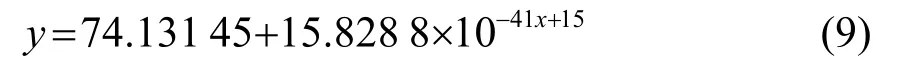
再对试件的相对非线性系数和抗拉强度之间的关系进行分析。结果如图12所示。
采用二阶多项式拟合方法对抗拉强度-相对非线性系数的关系进行拟合,得到拟合函数为

由图 12可以看出,抗拉强度随着相对非线性系数的增大而减小。随着试件塑性损伤的增大,由于损伤产生的非线性效应变大,体现在相对非线性系数的增大,而塑性损伤的增大导致了材料的抗拉强度降低。

图12 抗拉强度与相对非线性系数拟合曲线Fig.12 Fitting curve of tensile strength versus relative nonlinear coefficient
在相对非线性系数-应力三轴度组合预测的方法中,相对非线性系数和应力三轴度分别从检测信号和试件应力状态两个方面对试件进行更全面的评价。
再取5个完好的6061铝合金试件A6、A7、A8、A9、A10,在电子万能试验机上进行拉伸,试件 A6拉伸至塑性应变约为 4.5%,A7试件拉伸至塑性应变约为5.5%,A8试件拉伸至塑性应变约为5.75%,A9试件拉伸至塑性应变约为6.5%,A10试件拉伸至塑性应变约为 7.5%。分别对A6、A7、A8、A9、A10中部应力集中区域进行电磁超声非线性检测实验,得到超声表面波基波和二次谐波的幅值,计算出相对非线性系数,最后通过拉伸试验测得其抗拉强度,分析结果如表3所示。其中,预估值1是根据仿真分析得到的应力三轴度进行的预估,预估值 2是根据相对非线性系数进行的预估。

表3 电磁超声非线性检测的实验结果Table 3 Experimental results of electromagnetic ultrasonic nonlinear testing
进一步代入式(9)、式(10),对比预测抗拉强度值和实际值发现,试件A6、A7、A8通过特征参量相对非线性系数预测的抗拉强度(预估值2)误差较小,而试件A9、A10通过特征参数应力三轴度(预估值1)预测效果较好,结果如图13所示。即相对非线性系数可以更好地预测处于塑性损伤前期(4%≤ε<6%)的试件抗拉强度,而应力三轴度可以用于预测处在塑性损伤后期(6%≤ε<8%)的试件抗拉强度。

图13 不同应变(损伤)阶段的抗拉强度预估值和实际值对比Fig.13 Comparison of estimated and actual tensile strengths in different strain (damage) stages
由于试件塑性损伤前期,试件内部应力分布较为均匀,应力集中相对不明显,所以使得应力三轴度对这一阶段的损伤不敏感。而通过观察相对非线性系数的变化趋势发现,相对非线性系数在这一阶段变化较快,所以当试件处于塑性损伤前期可以选择相对非线性系数来进行抗拉强度的预测。处于塑性损伤的后期时,由于电磁超声接收信号信噪比低等问题使得相对非线性系数随塑性损伤变化趋于平缓,而此时由于试件内部的应力集中十分明显,应力三轴度变化较大,可以选择用应力三轴度进行抗拉强度的预测。结果表明预测相对误差小于5%,表现出了良好的准确度,证明了该方法的可行性。
综上所述,应力三轴度和非线性系数分别代表试件内部应力状态特征和电磁超声检测信号的频谱特征,从不同的方面反应了试件抗拉强度随塑性损伤的变化情况。由于两个参数随塑性损伤变化的趋势不同,使得这两个参数敏感的损伤阶段不同。把这两个特征参量结合进行抗拉强度的预测可以提高其预测的准确度。
4 结 论
首先,建立了电磁超声非线性检测塑性损伤试件的有限元三维仿真模型,计算试件的应力三轴度值,得到了应力三轴度随塑性应变的变化规律。其次,对不同塑性损伤试件进行电磁超声检测,可测得其相对非线性系数,得到相对非线性系数随塑性应变的变化规律。再通过电子万能试验机测得不同塑性损伤试件的抗拉强度,发现试件的塑性应变越大,其抗拉强度越低,呈近似线性的关系。最后,在仿真和实验的基础上对相对非线性系数-抗拉强度的关系以及应力三轴度-抗拉强度的关系进行了量化分析,由于这两个特征值随塑性损伤变化的趋势不同,使得这两个特征值敏感的损伤阶段不同。根据这两个特征值的损伤敏感程度来分阶段预估试件的抗拉强度并进行复合预测,可以提升预测的准确度。
