两种流道截面形式板式换热器传热性能及流动流阻力性能数值模拟分析

张元吉，李治国，张涛

（兰州兰石换热设备有限责任公司，甘肃兰州 730314）

1 前言

板式换热器是由一系列通过压型而具有一定波纹形状的金属薄板组装而成的换热器。与其他换热器相比板式换热器是一种高效、节能、紧凑的换热设备。据统计，在现代化学工业中换热器的投资大约占设备总投资的30%，在炼油厂中占全部工艺设备的40%左右，海水淡化工艺装置则几乎全部是由板式热交换器组成的。国外自20 世纪30 年代开始,板式换热器的应用已非常普遍。我国20世纪70年代, 开始批量生产板式换热器, 当时大多用在食品、轻工、机械等部门。近年来板式换热器的应用已经扩大到民用建筑的集中供热、核电、电力、冶金及生物能源、船舶、石化、化工、食品、纺织、造纸、制药、余热发电、海水淡化及军工等领域[1-12]。

板式换热器主要的优点有传热效率高，结构紧凑，占地面积小，但其也存在压降大，流体动能损失大等问题。本文主要通过ANSYS-CFX流体分析软件，分析板式换热器三角形截面流道和梯形截面流道在相同板间流速下流道内速度场，压力场温度场的分布情况，对比分析出两种截面对流体流动的影响，进而确定板式换热器合理的流道截面形式，为板式换热器的优化设计提供设计依据。

2 计算模型参数及数学描述

2.1 模型参数

本文选取板式换热器三角形截面流道和梯形截面两种不同板型，进行分析。流体在板式换热器流道内流动具有周期性，为了降低后期软件的计算量，本例选取板式换热器板片主换热区的一部分(100mmX100mm)进行数值模拟，三角形截面板片对应的换热板片为板片A,梯形截面流道对应的换热板片为板片B，两种不同截面流道对应板片的相关参数如表1所示：

表1 两种不同截面流道对应板片的相关参数

两 种 不同截面流道在solidworks中建立的三维模型如图1，图2所示。

图1

图2

3 数学模型

3.1 ANSYS-CFX的计算模型选取及控制方程

Ciofalo等利用有限元法和低雷诺数时的k-ε模型,对波纹板式换热器过渡区和弱紊流状态进行了数值模拟研究,可为其他板式换热器数值计算研究提供参考。本文选取由Yakhot和Orzag提出的RNG k-ε湍流模型[13]。RNG k-ε模型相比标准k-ε模型,做了下述改进:

1)通过修正瑞流流动粘度项,对平均流动中的旋转流流动情况加以考虑。

2)通过对S项改进,反映出主流的时均效应率,从而使模型中产生项与流动情况无关,同时在相同的问题中任然是空间坐标的函数。

3)与标准k-ε模型相比, RNG k-ε模型为瑞流普朗特数(Pr)提供了一个解析公式。

4) RNG k-ε模型对于高应变率以及流线弯曲程度较大的流动效果更好。

5) RNG k-ε模型提供考虑地低雷诺数的解析公式,可通过结合壁面函数计算低雷诺数效应。

综上所述, RNG k-ε模型更加适用于研究板式换热器的瑞流问题。RNG k-ε模型的瑞流动能方程(k方程)和端流耗散方程(S方程)为:

RNG k-ε模型

式中Gk—表示由层流速度梯度产生的瑞流动能;

Gk一表示由浮力产生的瑞流动能;

G1ε=1.42, G2ε=1.68—模型常量;

αk,αε— k方程和ε方程的瑞流普朗特数;

Sk, Sε—根据条件自定义;

相关的控制方程如下：

质量守恒方程：

i方向直角坐标系中的动量守恒方程：

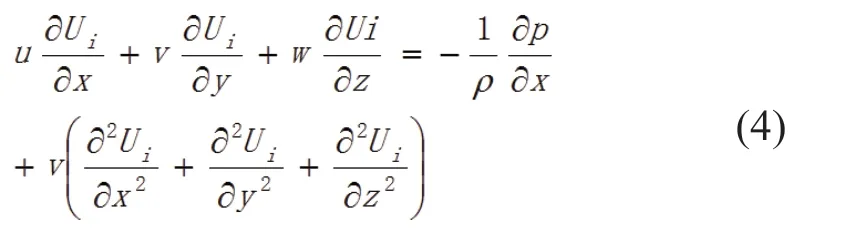
能量守恒方程

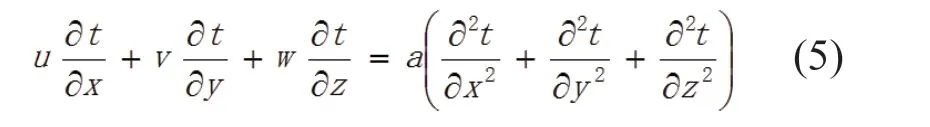
式中： U、V、W为流动速度分量；

ρ为流体密度；

Р为压力；

V为运动粘度，

Ui为i方向的速度分量；

a为热扩散系数，m2/s。

3.2 网格划分

网格类型、数量、尺寸大小是否合理是进行数值模拟计算过程中非常关键的一步，网格质量的优劣直接影响到模拟过程的收敛速度和计算结果的精准［14］本研究采取ICEM 划分网格,由于板式换热器板间流道几何结构较为复杂,因此网格类型主要采用非结构化四面体网格。选定了网格类型,另一个重要的因素是网格的数量和分布。通过加密传热壁面的网格后模型的总网格数分别为：三角形截面流道模型1161491个，梯形截面流模型117252个。

3.3 边界条件及假设

入口设置为流量入口，入口温度设置为25℃，压力统一设置为1.0Mpa。出口流速的选取不宜过高或者过低，流速高换热系数高，但是流体的阻力降也急剧增大，流速过低流体就达不到湍流状态且会形成较大的死角区一般板间平均流速为0.2～0.8m/s。[15]本研究流速选取出口流速为0.8m/s，。上下两侧边界设置为对称边界条件。

由于研究的介质为水，且流道内温差较小，没有相变，故作以下假设：

(1) 流体各物理量不随时间变化，为单相流体，定常流动。

(2) 流体为不可压缩的牛顿流体。

(3) 重力和浮升力影响忽略不计。

(4) 忽略流体流动时的黏性耗散作用所产生的热效应。

4 计算结果及分析

4.1 两种不同截面流道对流体流动阻力的影响分析

通过CFX后处理程序分别模拟得到三角形截面流道和梯形截面流道内流体流动情况。图3为三角形截面流道内流体流线分布图，图4为梯形截面流道内流体流线分布图。通过比较发现三角形截面流道内由于板片间触点为点接触，接触面积较小，其触点周围流线较平滑，不宜形成漩涡，而梯形截面流道由于流道内由于板片间触点为线接触，接触面积较大，其触点周围流线扰动较为剧烈，宜形成漩涡。

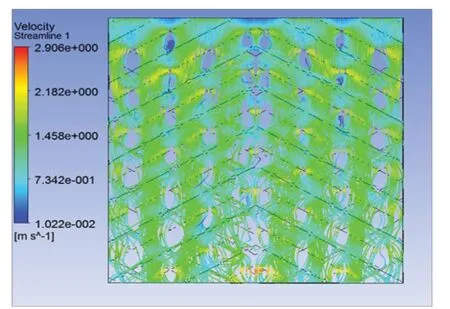
图3

图4

4.2 两种不同截面流道板间压降分析

通过比较发现三角形截面流道内由于板片间触点为点接触，接触面积较小，其触点周围压力分布较为均匀，而梯形截面流道由于流道内由于板片间触点为线接触，接触面积较大，其触点周围压力变化较大。通过软件计算得到流体通过三角形截面流道后流体压降损失为3808Pa,通过梯形截面流道后流体压降损失为5321Pa。结果表明，梯形截面流道的压降损失比三角形截面流道的压降损失高约28%。图5为三角形截面流道内流体压降分布图，图6为梯形截面流道内流体压降分布图。

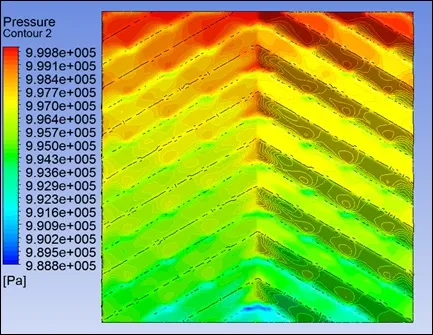
图5

图6

5 两种不同截面流道对传热性能的的影响分析

通过比较发现三角形截面流道内由于板片间触点为点接触，接触面积较小，其触点周围流体速度变化较小，而梯形截面流道由于流道内由于板片间触点为线接触，接触面积较大，其触点周围流体速度变化较大。结果表明梯形截面流道触点两侧及后方流体介质速度变化非常强烈，能够有效克服边界层效应，形成了较强的湍流，因此强化传热效果明显。三角形截面流道触点周围介质速度变化不大，因此强化传热效果不明，图7为三角形截面流道内流体速度矢量分布图，图8为梯形截面流道内流体速度矢量分布图。

图7

图8

6 结论

(1) 板式换热器压降损失及传热效果不仅与板片的波纹形式、波纹夹角、波纹深度有关而且还与流道截面形状和板片间触点的大小有关。

(2) 梯形截面流道由于板片触点呈线接触，接触面积大，因此压降损失较大。三角形截面流道由于板片触点呈点接触，接触面积小，因此压降损失较小。通过模拟结果表明，梯形截面流道的压降损失比三角形截面流道的压降损失高约28%。

(3) 梯形截面流道触点两侧及后方流体介质速度变化非常强烈，能够有效克服边界层效应，形成了较强的湍流，强化传热效果明显。三角形截面流道触点周围介质速度变化不大，因此强化传热效果不明显。