基于GA-BP的压缩机数据驱动建模研究
2022-03-11王佳文胡晓微
王佳文,胡晓微
(天津商业大学 机械工程学院,天津 300134)
对于制冷热泵系统,性能优化是目前研究的重点,而优化的前提是对制冷热泵系统进行准确的性能计算.压缩机是制冷热泵系统的核心,建立准确的压缩机模型对整个系统的优化设计有着重要的意义[1].影响压缩机运行的因素很多,所以用具体的公式精确表示比较困难,特别对于压缩机变工况或者超工况运行的情况,压缩机理论计算模型将难以计算,而对一些如容积系数、泄露系数等影响因素的表达使用较为简单的经验公式或经验系数[2],导致压缩机性能的计算很难精准,而且机理模型很难深刻地表现出实际压缩机的非线性和时变特性[3].
在实际使用过程中可以获得大量压缩机工作数据,这就为数据驱动建模提供了坚实的基础.数据驱动建模利用压缩机实际工作过程中产生的数据,进行数据挖掘,找到数据中某种相互对应的关系,在不涉及压缩机内部机理分析的情况下构建输入变量与输出变量之间的数学关系[4],是一种高效准确的“黑箱”建模方法.一直以来,利用数据驱动对压缩机建模得到了广泛地运用.AHRI10系数[5]模型不涉及任何制冷剂物性和压缩机内热力学计算,模型简单且在压缩机设计工况下有着较好的计算效果;李真[6]利用数据驱动建模中的参数辨识方法,辨识得到了喷射器-压缩机的3参数模型和4参数模型,在预测压缩机出口质量流量时,两者的均方根误差分别为2.89%和2.64%,实验结果表明,基于数据驱动建立的模型在所有工况下有着较高的准确性;Ma等[7]提出了一种基于数据驱动分析的涡旋压缩机建模方法,实验结果显示预测压缩机排气温度与排气流量结果与实验数据的最大误差小于10%;武鑫[8]基于非对称支持向量机算法结合离心压缩机的输入输出数据建立了离心压缩机喘振预测模型,利用模型可以识别压缩机新的喘振点,用预测结果结合控制系统避免压缩机在喘振区域运行.Chu等[9]基于多元统计分析原理,利用核偏最小二乘算法(KPLS)建立了离心压缩机的性能预测模型,结果表明,模型在预测压缩机压缩比和指示效率时,其均方根误差在5%以内.
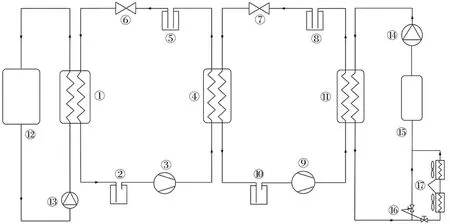
①—低温蒸发器;②⑩—气液分离器;③—低温压缩机;④—蒸发冷凝器;⑤⑧—储液罐;⑥⑦—电子节流阀;⑨—高温压缩机;—高温冷凝器;—恒温水箱;—水泵;—高温水泵;—高温储水罐;—阀门;—散热器图1 复叠式热泵实验流程图Fig.1 Flow chart of cascade heat pump experiment
BP人工神经网络由于其有强大的非线性映射能力,完善的自我学习能力,兼顾一定的推广、概括能力,使其广泛应用于数据驱动建模中[10-11].但BP人工神经网络存在过拟合、易陷入局部最小值、学习速率固定、收敛速度慢、鲁棒性能不好等缺点,而利用遗传(GA)算法可以优化BP人工神经网络[12],避免其陷入局部最优值.据此本文分别建立了压缩机的机理模型、BP模型和GA-BP模型,对压缩机进行数据驱动建模研究,通过对比3种压缩机模型性能,寻找合适的压缩机“黑箱”模型,为准确且简单地建立压缩机模型提供新的高效且准确的方法.
1 实验装置
建立了复叠式高温热泵实验系统,实验中低温循环选用涡旋压缩机,高温循环选用活塞压缩机.实验可研究不同工况下压缩机性能的变化,也为数据驱动建模提供历史数据支持.实验系统流程图如图1所示.
复叠式高温热泵系统主要分为4个循环:热源水循环、低温段工质循环、高温段工质循环和高温水循环.热源水循环回路包括加热水箱和循环水泵.高温水循环回路包括储水罐、高温水泵和散热风机,当高温水循环系统不能完全吸收高温冷凝器散发的热量时,开启散热风机,将热量散失到环境中,以此来保证系统的正常运行.实验测得数据包含:制冷剂流量、蒸发器进出口温度、冷凝器进出口温度、压缩机进出口压力和功率、热源水进出口温度和流量、冷却水进出口温度和流量.这些数据用于建模及其性能测试.
2 压缩机建模方法
压缩机的主要性能参数包括压缩机输出功率、压缩机输气量和压缩机排气温度,以这3个参数为目标进行建模.
2.1 压缩机纯机理模型
复叠高温热泵系统包括2台压缩机,分别为高温和低温压缩机.其中,高温为活塞压缩机,低温为涡旋压缩机.两种制冷压缩机的机理模型如下所示[13-14].
2.1.1 活塞压缩机模型 压缩机理论输气量计算公式如下:
(1)
其中:D表示气缸直径;S表示活塞行程;n表示转速;Z表示压缩机气缸数.
Vr=Vthγ
(2)
其中:Vr表示实际排气量;γ表示输气系数,它是与温度、压力、泄露系数有关的复杂系数.
压缩机的功率计算:
(3)
(4)
压缩机出口温度计算:
(5)
其中:Pi和Pm表示压缩机理论功率和输入功率;μmμi表压缩机的机械效率和电效率;Pdis和Psuc分别表示压缩机排气压力和进气压力;m表示压缩机多变指数,R245fa一般取1.14[15];Tin和Tout表示压缩机进出口温度.
2.1.2 涡旋压缩机模型 压缩机的理论排气量:
Vth=nπP(p-2t)(2N-1)h/60.
(6)
其中:n表示电机转速;P表示涡旋体节距;t表示涡旋体壁厚;h表示涡旋体高度;N表示压缩腔数.
压缩机的实际排气量:
Vr=μVVth.
(7)
其中:Vth表示压缩机理论输气量;μV是涡旋压缩机输气系数,它是与温度、压力、泄露系数有关的复杂系数.
(8)
(9)
压缩机出口温度计算:
(10)
其中:Pi和Pm表示压缩机理论功率和输入功率;μmμi表压缩机的机械效率和电效率;Pdis和Psuc分别表示压缩机排气压力和进气压力;m表示压缩机多变指数,R134a一般取1.14[16];Tin和Tout表示压缩机进出口温度.
2.2 BP人工神经网络
人工神经网络是仿生人脑神经元抽象化后建立的人工智能算法[17],原理是用神经网络将输入参数与输出参数形成某种没有具体公式的对应关系,再将输入参数放入训练好的网络模型对输出参数预测.而BP神经网络是应用最广泛的人工神经网络模型,它由信息的正向传播和误差的反向传播2个过程组成.通过对输出结果的误差来对权值和阈值进行更新,BP人工神经网络模型的建立主要涉及以下几个方面,包括输入和输出参数合理的选择、隐含层中间节点数的选择、初始权值和阈值的优化等.
2.3 输入输出参数的选择
神经网络的构建需要选取合理的输入输出参数.虽然神经网络模型不关注具体的物理过程,但是研究对象本身是含有明确物理意义的,每个输出参数和输入参数之间都有明确的物理对应关系.如果随意选取输入输出参数,可能给神经网络模型提供错误的信息.利用相关性分析,可以根据输出参数有效确定输入参数.
在前文中已经确定了压缩机输出功率、压缩机输气量和压缩机排气温度为输出参数,再进行相关性分析得出,影响这3个压缩机性能指标的参数包括压缩机进出口压力与压缩机进口温度,所以将这3个参数作为BP人工神经网络输入参数,且这3个输入参数也与机理模型计算所需输入参数保持一致,这使其两种建模方法对比结果更具说服力.
2.4 最佳中间节点数的确定
确定隐含层神经元个数的办法是在确定了输入层及输出层神经元的个数情况下,通过反复调试网络模型得到合适值.利用线性回归法对不同的网络结构进行分析比较,确定最佳的中间节点数.这种方法为试凑法.图2显示,当隐含层节点数为8时,神经网络的拟合标准差最小,这表明此时的神经网络的性能最佳.由此选择隐含层节点数为8.
综上所述,确定了BP人工神经网络应用于压缩机建模上的拓扑结构,为3-8-3结构,是多输入多输出结构,即3个输入参数,中间隐含层为8个节点,3个输出参数,如图3所示.
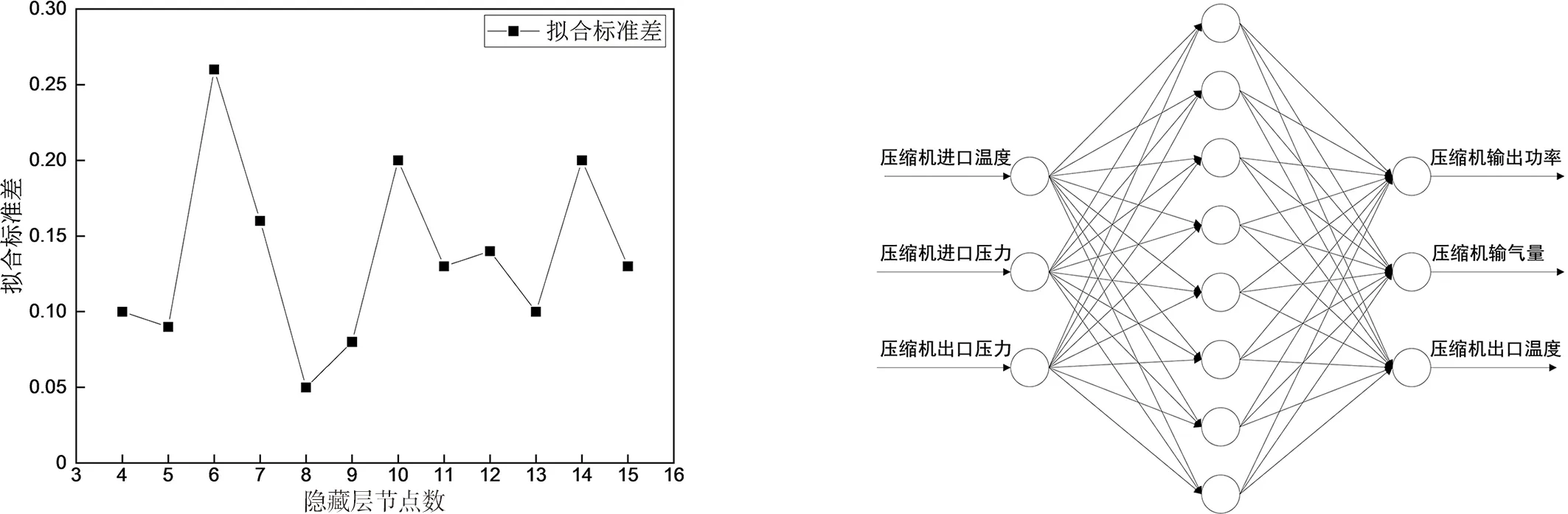
图2 中间节点数对神经网络性能影响图 图3 BP人工神经网络结构示意图
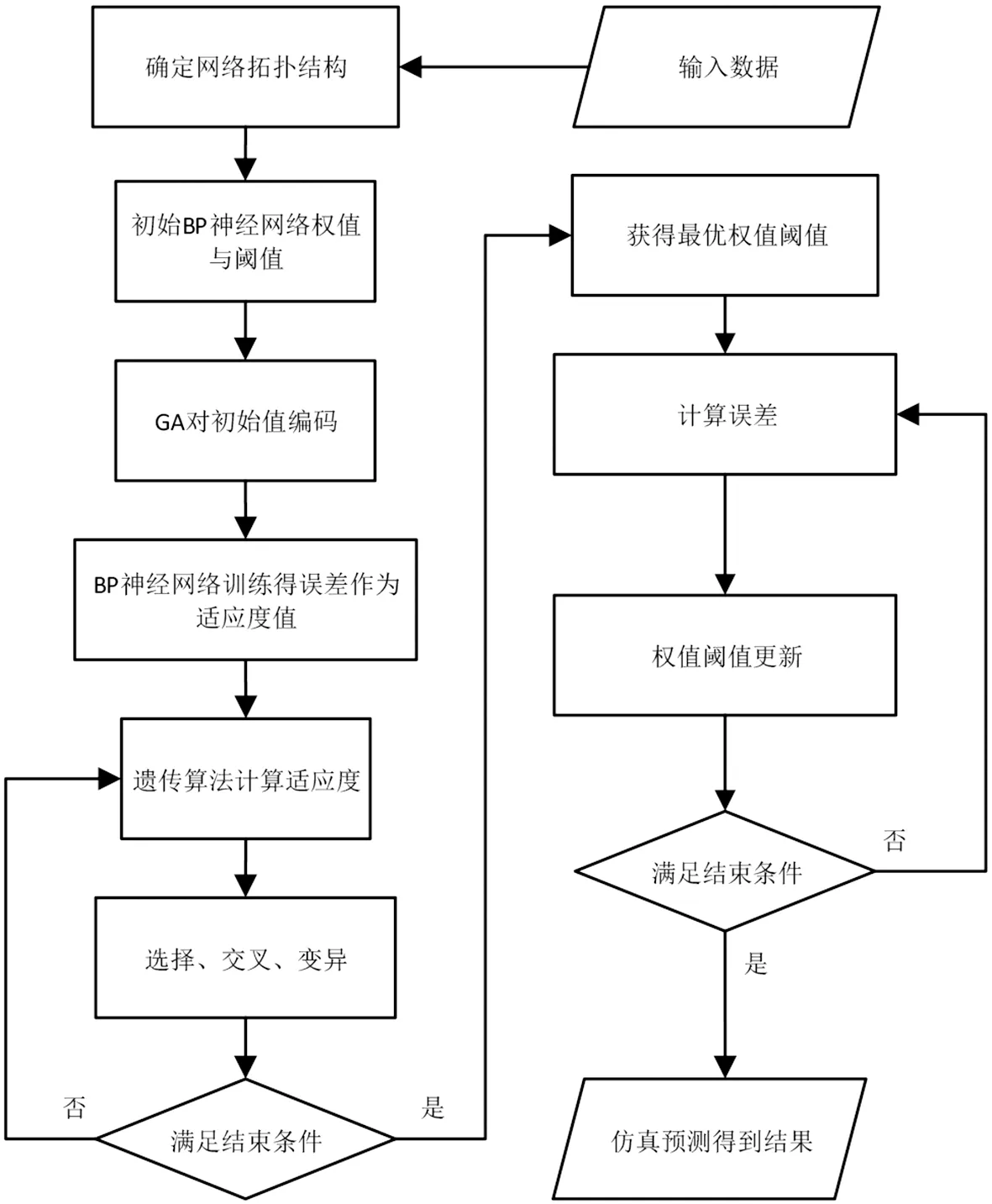
图4 GA算法优化的BP人工神经网络流程图Fig.4 Operation flow chart of BP artificial neural network optimized by GA algorithm

表1 模型预测结果平均相对误差Tab.1 Average relative error of model prediction results
2.5 遗传算法优化的BP人工神经网络
遗传算法(GA)是一种通过模拟自然进化过程搜索最优解的方法,该算法通过数学的方式,将最优值问题的求解过程转换成类似生物进化中基因遗传过程,相对一些常规的优化算法,通常能够较快地获得较好的优化结果.
其优化的过程为:在确定了BP神经网络的结构以后,将神经网络的初始权值和阈值输入到遗传算法中,将神经网络训练后的误差作为适应度值,然后对神经网络的权值和阈值进行最优化搜索,得到最优的权值阈值后,将其代入到神经网络的训练和预测过程中,最后得到预测结果.图4为GA-BP人工神经网络流程图.
3 模型预测结果与性能分析
依托于高温复叠式热泵系统试验台,本次模型建立的数据所处工况如下:热源温度为30 ℃,高温冷凝器出水温度为60~122 ℃.数据共200组,分为训练集和测试集.训练集有190组,范围是高温冷凝器出水温度为60~115 ℃;测试集有10组,范围是高温冷凝器出水温度为116~122 ℃.这样划分训练集和测试集不仅可以检测模型的准确性,也可以检测模型的外推性.
3.1 模型预测结果分析
分别用3种模型预测测试集的10组样本,分别预测高低温压缩机功率、输气量及出口温度,3种模型的预测结果平均相对误差如表1所示,预测结果如图5、6所示.
图5和图6中的(a)、(b)、(c)分别表示3种模型预测的压缩机功率、压缩机输气量和压缩机出口温度与实测值的对比图.从图5、6可以看出,无论是高温压缩机还是低温压缩机,GA-BP模型的预测值是最接近实验数值的,机理模型的值则是偏离实测值最大的.结合表1、图5和图6,可以得出以下结果.
在预测高温压缩机功率时,GA-BP模型相较于BP模型和机理模型,平均相对误差分别下降了3.75%和8.83%,平均相对误差只有0.53%,在预测低温压缩机功率时相较于BP模型和机理模型,平均相对误差分别下降了1.05%和8.49%,平均相对误差只有0.74%.在预测高温压缩机输气量时,GA-BP模型的平均相对误差相较于BP模型和机理模型则分别下降了0.22%、5.01%,GA-BP模型的平均相对误差只有0.67%.在预测低温压缩机输气量时,GA-BP模型的平均相对误差相较于BP模型和机理模型则分别下降了2.57%、6.29%,GA-BP模型的平均相对误差只有0.42%.在预测高温压缩机出口温度时,GA-BP模型的平均相对误差相较于BP模型和机理模型则分别下降了0.24%、0.84%,GA-BP模型的平均相对误差只有0.23%.在预测低温压缩机出口温度时,GA-BP模型的平均相对误差相较于BP模型和机理模型则分别下降了1.3%、0.76%,GA-BP模型的平均相对误差只有0.21%.
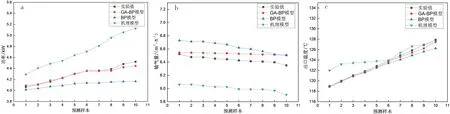
图5 高温压缩机机理模型与数据驱动模型高温压缩机性能预测值与实测值对比Fig.5 Comparison between the predicted and measured performance values of high temperature compressor and its mechanism model and data-driven model
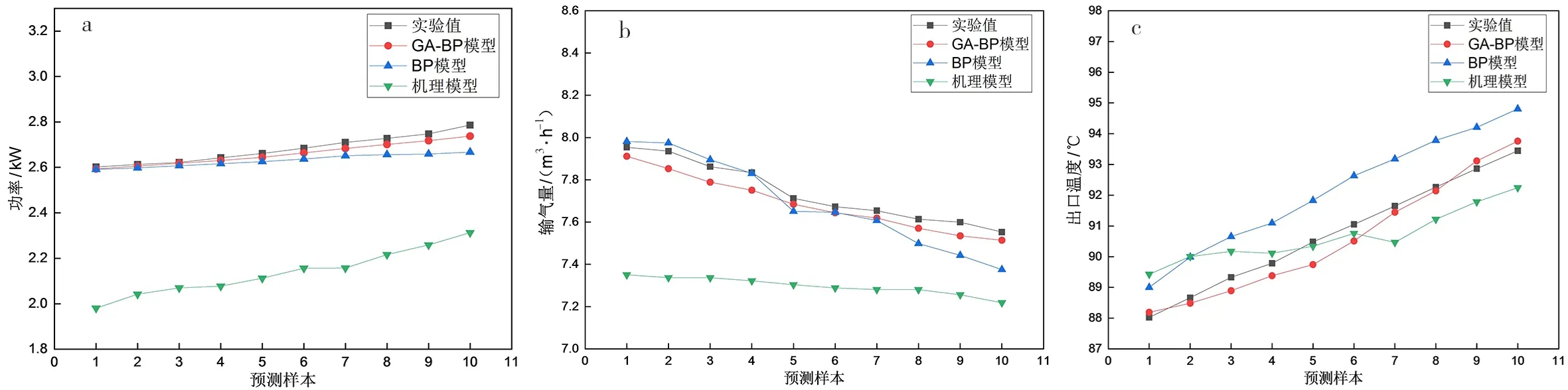
图6 低温压缩机机理模型与数据驱动模型低温压缩机性能预测值与实测值对比Fig.6 Comparison between predicted and measured performance values of low temperature compressor based on mechanism model and data-driven model

表2 高低温压缩机不同模型预测结果性能评价Tab.2 Performance evaluation of different models of high and low temperature compressors
可以发现,与压缩机的机理模型相比较而言,数据驱动模型的结果更加准确,平均相对误差在4%以内,且平均相对误差有着较大地提升.这是由于压缩机在超工况下运行,机理模型计算式中经验系数选择较为困难,导致机理模型的结果出现较大偏差,而数据驱动模型则避免了这个问题,得到了较为准确的结构.而GA-BP模型相对BP模型,其预测结果更加精确,其平均相对误差均在1%以内,这是由于GA算法利用全局搜索,得到了BP神经网络的最佳初始权值和阈值,使得神经网络的预测结果更为准确.
3.2 模型性能评价
混合模型性能评价指标为RMSE和R2.两个指标的公式如下.
(11)
(12)

从表2可得,对于高低温压缩机3种性能参数预测模型,GA-BP模型的RMSE和R2值都非常接近最优值,这说明GA-BP模型的预测性能在3种模型之中是最佳的.
在RMSE值的对比中,高低温压缩机3个性能参数GA-BP的数值分别为0.034、0.024,0.073、0.129和0.323、0.383,其数值非常接近目标值,这说明其模型预测结果误差极小,而机理模型与BP模型的值就与目标值有一定的偏离,这说明其模型预测结果与实测值还有较大的误差.因此,GA-BP模型有着较好的预测准确性.同样的,在R2值的对比中,高低温压缩机3个性能参数GA-BP的数值分别为0.817、0.861,1.003、1.329和0.961、1.008,其数值也是十分接近目标值,这说明,模型有着较好的预测外推性.而机理模型在预测低温压缩机功率和排气量时,R2值与目标值偏离较大,为9.318和9.468,这是因为机理模型在计算这两个性能参数时,需要选择工况下合适的经验系数和制冷剂的多变指数,而两者的选择在超工况下又十分困难,这使得其拟合性能较差.
4 结论
对复叠式热泵系统高低温压缩机进行了数据驱动建模的研究,建立了压缩机机理模型、BP模型和GA-BP模型,通过高低温压缩机功率、输气量和出口温度等参数的预测,对比分析每个模型的性能,得出以下结论:
1) 3种模型中,机理模型的误差最大,预测性能最差.这是由于其计算涉及经验系数的选择,面对复杂的运行工况时预测能力较差.
2) BP模型和GA-BP模型都有着较好预测性能,其对3种性能参数预测的结果平均相对误差在4%以内,这说明BP人工神经网络这种数据驱动模型应用于压缩机性能建模有着良好的性能.
3) GA-BP模型相较于BP模型有着更好的预测性能,其平均误差均在1%以内,说明GA算法很好地优化了BP模型,具有较好的实际应用价值.
