铁损对直驱式永磁同步风力发电机组特性的影响

陈 谦,高仕红,马紫琬,董岳昆,黄 京

(湖北民族大学 信息工程学院,湖北 恩施 445000)

为加快实现我国“碳达峰、碳中和”的目标，大规模发展可再生能源、优化能源系统结构成为当前形势下能源电力的发展之重[1].目前，各类可再生能源中风力发电技术发展最快，对其开展更深入的研究尤为重要，要求风电系统的建模尽量模拟实际情况[2].

直驱式永磁同步风力发电机组(direct-drive permanent magnet synchronous generator,D-PMSG)凭借结构简单、运行噪声小、维护工作简便的优势被重视并广泛应用.在构建D-PMSG的发电机数学模型时，为了简化计算，通常都将发电机的铁损部分作忽略处理，只列出其基本方程式[3-4].然而在实际发电机组的运行过程中，定子铁损是真实存在的，如果忽略发电机的铁损来研究和模拟D-PMSG的运行情况，就有可能与实际机组的运行情况存在偏差，导致某些仿真结果的准确度降低.

尹明等[5]建立了包括风力机模型、传动系统模型、发电机模型的D-PMSG数学模型，并在Matlab中进行了仿真验证；高剑[6]建立了D-PMSG的参数解析模型，并研究了发电机极数与发电机铁心损耗间的解析关系；Urasaki等[7-9]讨论并介绍了考虑电机各种损耗的电路模型，提出了考虑铁心损耗的永磁同步电机的并联电路模型与串联电路模型，推导并验证了两种电路模型在数学意义上的一致性，并给出了基于P-Q关系图下的永磁同步电机等效铁损电阻的参数测量方法；高仕红等[10]提出了考虑铁损时的永磁同步电机的数学模型，并在Matlab中得到了验证.本文将D-PMSG与考虑铁损的永磁同步电机相结合，建立考虑发电机铁损的D-PMSG模型，并在Matlab/Simulink环境中与未考虑铁损的D-PMSG模型做比较，通过仿真结果研究铁损对D-PMSG运行时电气特性、电气特性的影响，验证考虑铁损的D-PMSG模型的有效性与考虑铁损的必要性.

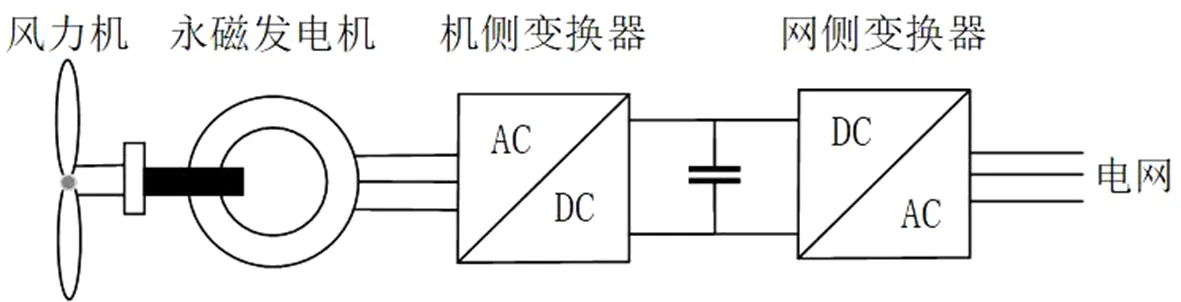
图1 直驱式永磁风力发电系统的整体结构Fig.1 Structure of direct-drive permanent magnet wind power system

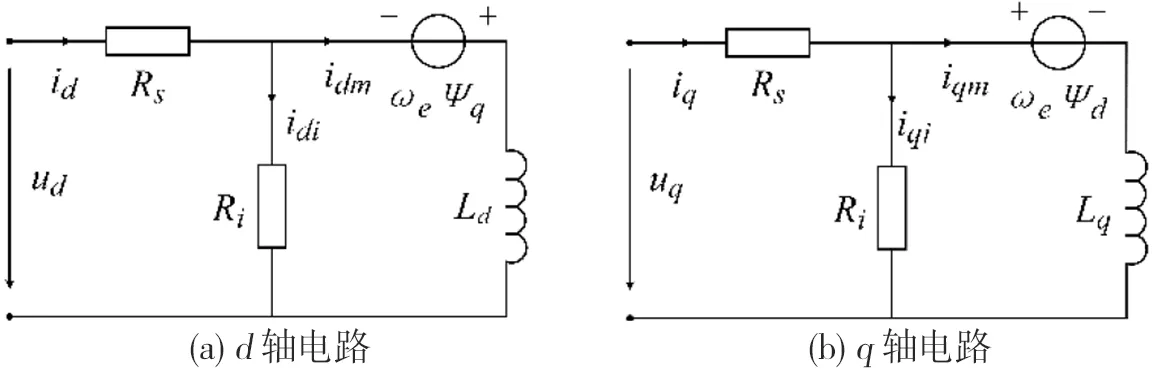
图2 考虑铁损时的d-q轴等效电路Fig.2 d-q axis equivalent circuit considering iron loss

1 D-PMSG的数学模型

D-PMSG系统整体结构如图1所示，包括机侧、网侧两部分.对D-PMSG机侧仿真建模需要考虑：空气动力系统模型、永磁同步发电机模型[11].

1.1 空气动力学数学模型

风力机建模将风速Vw作为输入，机械转矩Tw、机械功率Pw作为输出，其数学关系为

(1)

式(1)中，ρ为空气密度；R为风力机叶轮半径；Cp为风能利用系数；ωw为风轮角频率；λ为叶尖速比.

风力发电机组传动结构的数学关系为

(2)

式(2)中，Jeq为风电机组的等效转动惯量；Bm为转动粘滞系数；Te为电磁转矩；ωg为发电机转子机械角频率，且等于风轮角频率.

1.2 考虑铁损的永磁同步发电机数学模型

永磁同步发电机的定子铁损由磁滞损耗、涡流损耗两部分组成[12].在d-q旋转坐标系下建立考虑铁损的永磁同步风力发电机的电路模型，如图2所示.

图2中，id、iq为d、q轴电流分量；idi、iqi为d、q轴等效铁损电流分量；idm、iqm为d、q轴有功电流分量；Ld、Lq为d、q轴同步电感；ud、uq为d、q轴电压分量；Ψq、Ψd为d、q轴磁链分量；Rs为定子电阻；Ri为等效铁损电阻；ωe为转子电角频率.

D-PMSG的同步发电机建模中，往往需要考虑电压方程、电流方程、电磁转矩方程.结合D-PMSG的建模特点，以电压、电磁转矩作为输入量，电流作为输出量，idm、iqm、idi、iqi作为中间变量，即可建立考虑铁损的永磁同步发电机模型.由图2可列出考虑铁损的永磁同步发电机的回路电压、节点电流、磁链方程，联立推得

(3)

(4)

(5)

(6)

其中，p为微分算子；Ψf为转子永磁体磁链.

假设d、q轴电感相等，永磁同步发电机的电磁转矩表达式可被简化为

Te=1.5npΨfiqm.

(7)

2 D-PMSG的控制策略

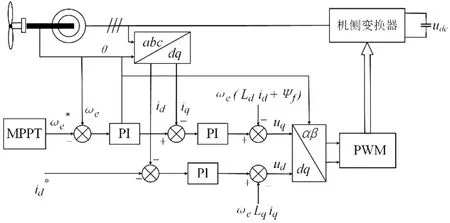
图3 D-PMSG整体控制框图Fig.3 Diagram of D-PMSG control

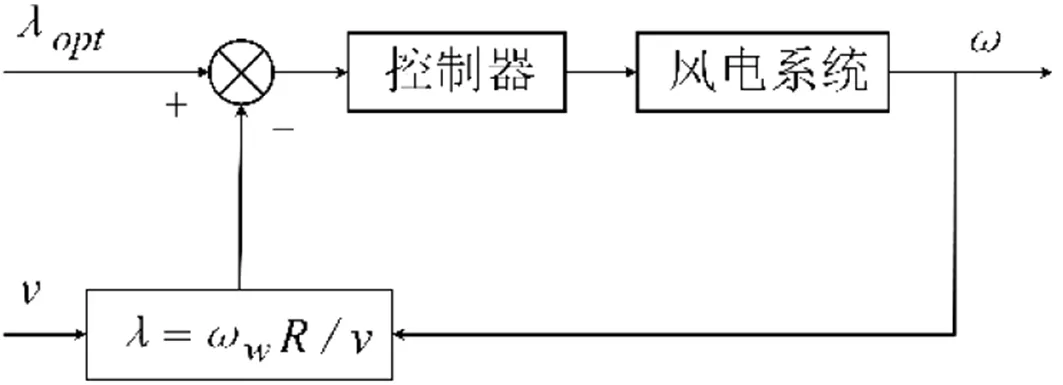
图4 TSR结构Fig.4 Structure of TSR

图5 永磁发电机转速控制Fig.5 Speed control of PMSG

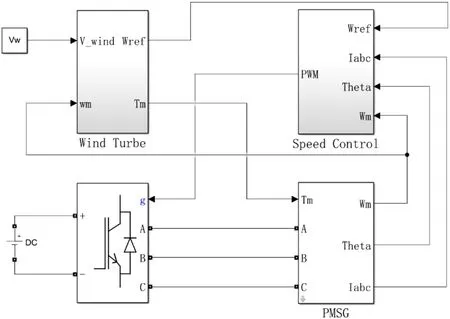
图6 D-PMSG模型Fig.6 Model of D-PMSG

控制环节在D-PMSG建模中也极为关键，通常需要考虑最大功率跟踪(maximum power point trackers,MPPT)控制、电机转速控制.D-PMSG的整体控制框图如图3所示.

2.1 MPPT控制

D-PMSG运行时存在的最大风能利用系数使得当前工况下的风力机能够捕获的风能量达到最大值[13].一般通过改变叶尖速比或者桨距角的方式以求得风电机组在较大风速范围内运行时保持最大风能利用系数，从而达到机组的最大功率.常用的MPPT控制方法有：最佳叶尖速比法(tip speed ratio,TSR)、功率信号反馈法(power signal feedback,PSF)、爬山搜索法(hill-climb searching,HCS).因为TSR控制简单且易于实现，精准度良好，所以本文采用TSR来实现MPPT控制，其结构如图4所示[14-15].

当发电机的转速与风机风速计算得到的叶尖速比与最佳叶尖速比不同时，产生误差信号，调节发电机转速直到此刻的叶尖速比与最佳叶尖速比相一致，从而实现最佳叶尖速比控制运行.

2.2 发电机转速控制

采用比例积分(proportion integration,PI)的控制方法，通过控制发电机的电磁转矩来实现永磁同步发电机的转速控制.因为电磁转矩与q轴电流线性相关，将d轴始终定位在转子磁链，使d轴电流分量保持为零，通过控制q轴电流分量来控制电磁转矩，进而控制发电机转速[16-17].转速控制如图5所示.

图5中，外环控制转速，内环控制电流.将测量到的发电机实际转速与额定转速作比较，并对比较后的偏差值进行PI控制，从而得到内环控制所需的q轴电流参考信号.

3 D-PMSG模型仿真验证及分析

Matlab/Simulink环境具有适应面广、模块库完备、仿真贴近实际、操作灵活度高等优点，在Matlab/Simulink中建立考虑铁损的D-PMSG模型，并建立不考虑铁损的理想D-PMSG模型作为对照.D-PMSG在Matlab/Simulink中的仿真建模如图6所示.具体参数如下：D-PMSG的额定功率PeN=2 000 kW；定子电阻Rs=0.006 Ω；铁损等效电阻Ri=0.23 Ω；定子d、q轴电感Ld=Lq=3 mH；极对数np=52；永磁体磁链Ψf=3.48 Wb；风轮半径R=32.5 m；额定风速vwN=12.5 m/s；转动惯量J=18×103kg/m3；空气密度ρ=1.224 kg/m3.

自然界中风速具有时变性，为综合考量铁损是否对D-PMSG特性造成影响，在Matlab/Simulink中对风速在t=0.4 s时从8 m/s增速跃变到12.5 m/s，t=0.7 s从12.5 m/s减速跃变回8 m/s的情况进行仿真，仿真时间为1 s.选取风能利用系数、风力机输出转矩表示D-PMSG的机械特性；发电机输出功率、发电机输出线电压表示D-PMSG的电气特性.

3.1 铁损对D-PMSG机械特性的影响

给出0.25～0.55、0.55～0.85 s的风能利用系数、输出转矩如图7所示.

(a) 0.25～0.55 s风能利用系数 (b) 0.25～0.55 s输出转矩 (c) 0.55～0.85 s风能利用系数 (d) 0.55～0.85 s输出转矩图7 风力机风能利用系数、输出转矩Fig.7 Diagram of Cp，Tm

稳态时考虑铁损的D-PMSG模型的风能利用系数数值与理想模型基本一致，在MPPT控制下均保持在0.47～0.48之间.由局部放大图可知与理想模型相比考虑铁损的D-PMSG模型存在小幅震荡，低风速时最大偏差为0.02%，额定风速时最大偏差为0.28%.

对比风速增加、减小的两种暂态运行情况可知，风速增加时考虑铁损的D-PMSG模型过渡时间更长，风速降低时考虑铁损的D-PMSG模型过渡时间较理想模型稍短，且减速跃变对D-PMSG的影响更大.铁损对D-PMSG的机械性能影响较小.

3.2 铁损对D-PMSG电气特性的影响

给出0.25～0.55、0.55～0.85 s的发电机输出功率、输出电压如图8所示.

(a) 0.25～0.55 s输出功率 (b) 0.25～0.55 s输出电压 (c) 0.55～0.85 s输出功率 (d) 0.55～0.85 s输出电压图8 发电机功率、电压Fig.8 Diagram of Pe，Uab

系统达稳态后考虑铁损的D-PMSG模型的输出功率较理想模型存在频率性的波动，由式(4)可知，考虑铁损后电流有功分量的计算式的系数存在电角频率，不再是常数，理论上仿真波形将存在与电角频率成比例的波动情况，该仿真波形与理论推导相符.比较稳态下两种模型的输出线电压波形可知，考虑铁损的D-PMSG波形存在严重的畸变现象，峰值处有明显缺口，考虑铁损的D-PMSG与理想D-PMSG模型的输出线电压峰值分别为909、796 V，使得考虑铁损的D-PMSG输出电压的有效值低于额定值.考虑铁损的D-PMSG模型滞后于理想模型约108°.

风速增加时考虑铁损的D-PMSG模型输出功率的过渡时间更长，但超调量比理想模型小，风速降低时两者过渡时长相近，但超调量远大于理想模型.铁损对D-PMSG的电气性能存在影响.综上，本文搭建的考虑铁损的D-PMSG仿真模型能够在一定程度上正确反映D-PMSG各物理量的运行情况.

4 结语

将考虑铁损的永磁电机数学模型与d-q等效电路相结合，并在Matlab中建立考虑铁损的D-PMSG模型，同时搭建不考虑铁损的D-PMSG理想模型作为对照，分析铁损对D-PMSG机械及电气特性的影响，仿真结果说明铁损对D-PMSG的机械性能影响较小，但对其电气性能存在一定影响，验证了该模型更贴近实际运行的D-PMSG机组.随着科技发展，对风力发电技术的研究更为深入，对D-PMSG进行仿真建模时有必要考虑铁损.