激光追踪系统机械结构拓扑优化轻量化方法
2022-03-11陈洪芳韩梦蕊孙若水石照耀
陈洪芳, 韩梦蕊, 孙若水, 石照耀
(北京工业大学 北京市精密测控技术与仪器工程技术研究中心, 北京 100124)
随着装备制造业的发展,在大型工件检测、工件对齐、机床校准等领域,对测量精度的要求越来越高,激光跟踪测量技术作为公认最具有潜力的可进行大范围、高精度动态现场实时测量技术,近年来受到广泛关注[1]。激光追踪仪由于其基准球的创新设计,使激光跟踪技术的空间距离的测量精度得到了大幅提高,解决了坐标测量机标定效率和精度提高难度大的问题。激光追踪测量系统采用类杠杆结构实现俯仰运动[2],利用配重块实现俯仰平台的平衡。在有限的激光追踪测量系统机械整体结构内,激光追踪测量系统俯仰平台配重块存在体积与质量的矛盾,极大影响了部分零件的使用寿命、测量系统精度及系统安全性能等。采用拓扑优化的方法进行机械结构的轻量化,克服了传统设计中对人的主观依赖性[3],特别是在工业部件轻量化中应用广泛。拓扑描述方法较为常用的是均匀化方法和密度法材料插值模型[4-5]。其中密度法材料插值模型在工程领域应用最为广泛。对于密度插值方法,不同插值模式会导致不同的计算模型,如SIMP材料插值模型、RAMP材料插值模型及Voigt上边界材料插值模型及等在工程中较为常用的为SIMP材料插值模型[6-8]。国内外学者对材料插值理论和拓扑结构优化方法及其应用进行了深入研究。如Nguyen等[9]提出将拓扑优化作为增材制造(3D打印)设计方法在保证产品的机械性能前提下,帮助设计者用最少的材料创造出最优的产品结构;李所军等[10]基于变密度法分别对摇臂和摆杆进行了多工况结构拓扑优化设计;张聪等[11]设计了7 个三体船结构强度校核工况并应用变密度拓扑优化方法分别计算了不同结构在不同工况下的应力分布,实现了部分结构的轻量化设计;Liang等[12]对变速箱在多工况下的拓扑优化进行了研究;Otomo等[13]提出了一种基于归一化高斯函数方法的新型两步拓扑优化方法,可有效地改善爪极式交流发电机的性能;Chen等[14]介绍了一种在拓扑优化敏感性过程中使用工程约束的启发式方法,使拓扑优化结果可以满足结构设计的要求;Cai等[15]提出了一种考虑载荷不确定性的鲁棒连续体结构拓扑优化问题的求解方法,采用的比例拓扑优化方法避免了计算目标灵敏度,并证明了所提方法的有效性。目前关于拓扑优化在机械机构轻量化设计的相关理论及应用较为完善[16]。但在激光追踪测量系统中应用相对较少。
本文基于三维拓扑优化算法[17],使用变密度法的SIMP材料插值模型[18],对激光追踪测量系统俯仰平台进行拓扑优化,根据优化结果在Inventor中进行模型重构,对重构模型进行应力分析,并计算配重进行验证。在不改变原有机械结构条件下,实现激光追踪测量系统的机械结构轻量化。
1 激光追踪测量系统机械结构的轻量化
1.1 激光追踪测量原理
将猫眼放置于被测目标上,当猫眼处于静止状态时,激光束入射到位置敏感探测器(position sensitive detector,PSD)的中心,PSD输出电压信号为零,电机无控制信号输入;在追踪测量过程中,猫眼运动,被猫眼反射回的激光束偏离PSD的中心,PSD输出偏移量信号反馈至电机,电机通过机械系统控制光学系统跟踪猫眼运动,保证光学系统发出的光始终入射到猫眼的中心,实现系统的跟踪测量[19]。激光追踪测量系统工作原理示意图如图1所示。

图1 激光追踪测量系统工作原理示意Fig.1 Light path diagram of Laser tracking measurement system
1.2 激光追踪测量系统机械结构
激光追踪测量系统整体结构[20]主要由4个部分组成:激光头部分,由光学元件及干涉光路等组成;俯仰平台,由激光头、防尘盖、连接板、俯仰架及配重组成;旋转平台,主要由俯仰电机及俯仰平台支撑架等组成;底座,主要由标准球、支撑座及旋转电机等组成,如图2所示。其中标准球球心位于两电机轴线交点处。
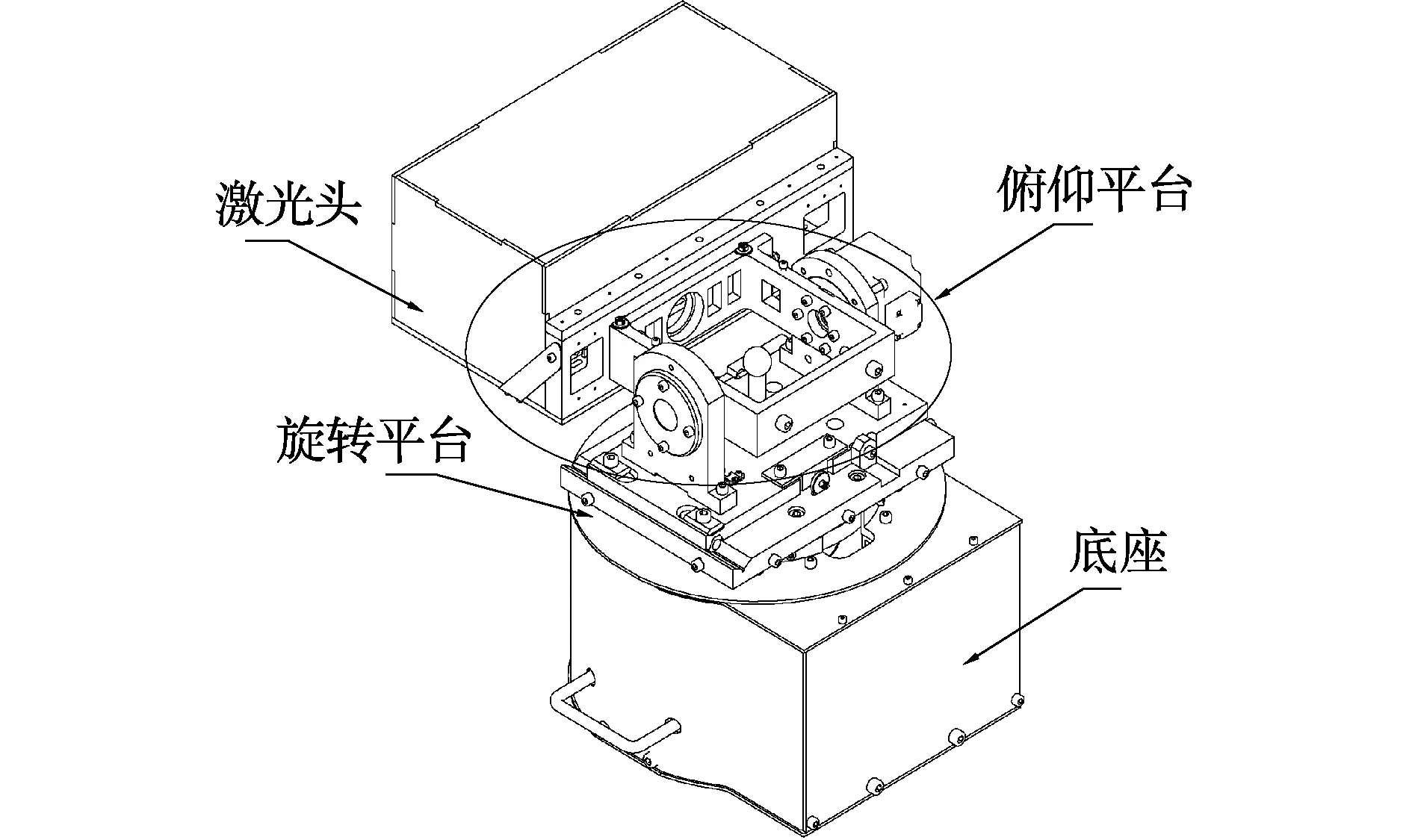
图2 激光追踪测量系统机械结构Fig.2 Mechanical structure of laser tracking measurement system
1.3 机械结构轻量化的拓扑优化理论
对于静力学,常用优化模型主要有:在体积或质量约束下求最小柔度(最大刚度)[21];或在刚度约束下求最小体积或质量[22]。本文采用约束体积,目标函数为最小柔度进行模型建立。
首先,将离散模型转化为连续体进行拓扑优化,建立目标函数,设置约束条件等,目标是让柔度最小化,表达为:
(1)
式中:U为整体位移;F为力矢量;K为整体stiffness矩阵(单元刚度矩阵,表示单元体的受力与变形关系);e为元素;xe为元素密度;ue为单元位移矢量;k0为单元杨氏模量的单元stiffness矩阵;ke为stiffness矩阵;x为设计变量矢量;xmin为最小相对密度矢量;N为用于离散设计域的元素数;p为惩罚幂(通常p=3);V(x)为材料体积;V0为设计域体积;f为规定的体积分数。
对连续体问题,可使用最优化准则(OC)法进行求解。OC优化方案可表达为[18]:
(2)
式中:m是正的移动极限;η(=1/2)是数值阻尼系数;Be可从最优性条件中得到。
根据OC优化准则可以计算出目标函数c的灵敏度。公式表达为:
(3)
式中:λ为拉格朗日乘子;Be为相对灵敏度。拉格朗日乘子可采用双分段算法求得,要使用过滤器对灵敏度进行优化迭代。
2 激光追踪测量系统机械结构的三维拓扑优化方法
表格的设基于激光追踪测量系统整体机械机构,若俯仰平台与激光头连接后的重心不在标准球中心,会导致俯仰电机和旋转电机轴向受力不平衡、系统精度下降等问题,需要在俯仰架后端增加配重。配重由于质量与体积之间的矛盾,因此要对俯仰平台前半段机械结构进行减重优化。如图3所示为激光追踪测量系统俯仰平台机械结构图,在俯仰平台中除配重外,质量最大的零件为连接板及俯仰架,本文将针对连接板及俯仰进行轻量化研究。
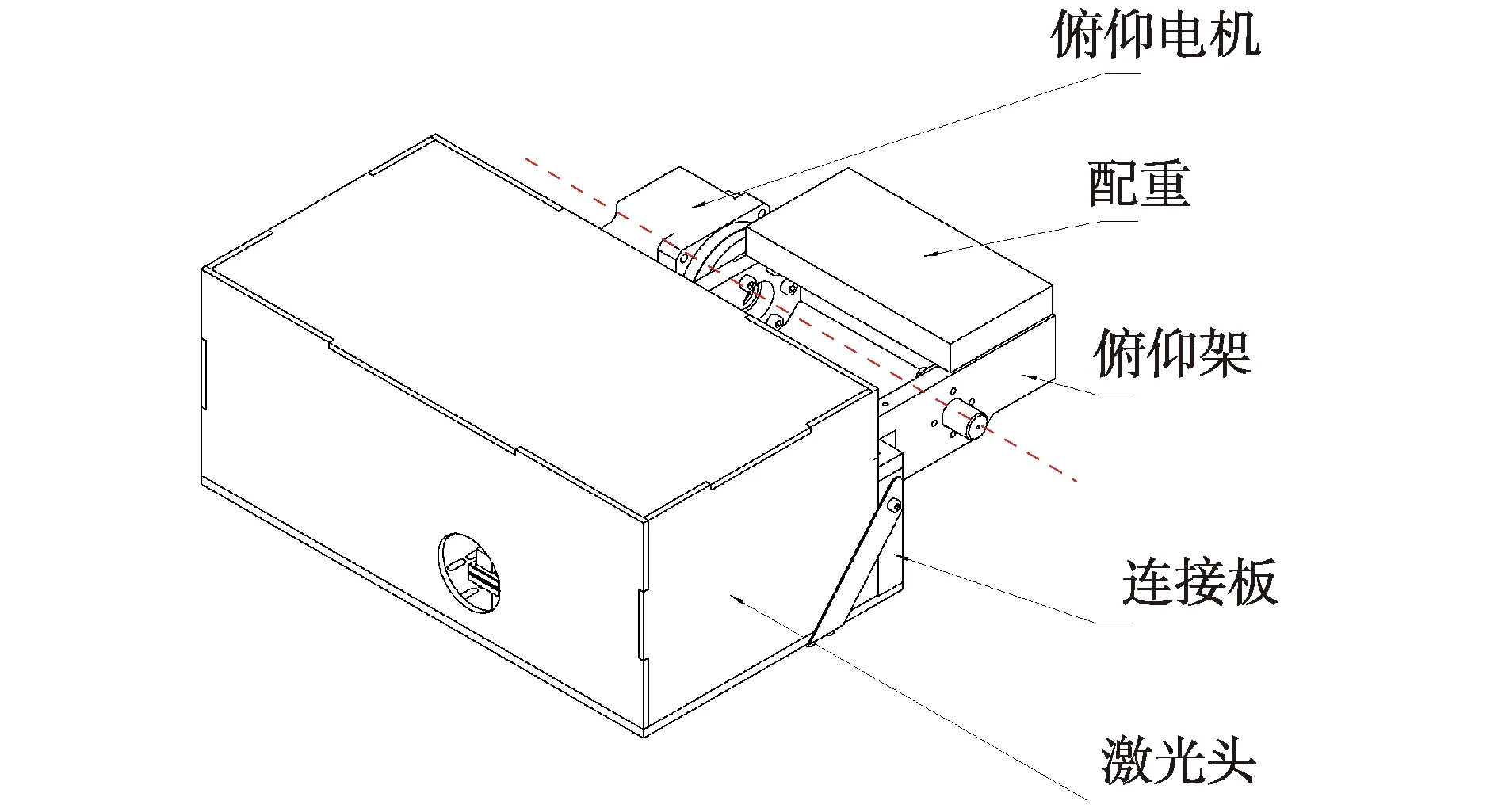
图3 激光追踪测量系统俯仰平台机械结构图Fig.3 Mechanical structure diagram of the pitch platform of the laser tracking measurement system
利用三维拓扑优化算法对连接板和俯仰架的机械结构进行优化,根据优化结果及实际情况进行俯仰平台的模型重构,并对重构模型进行力学分析,根据重构模型仿真出质量进行配重的重新计算,激光追踪测量系统机械结构的三维拓扑优化方法流程如图4 所示。
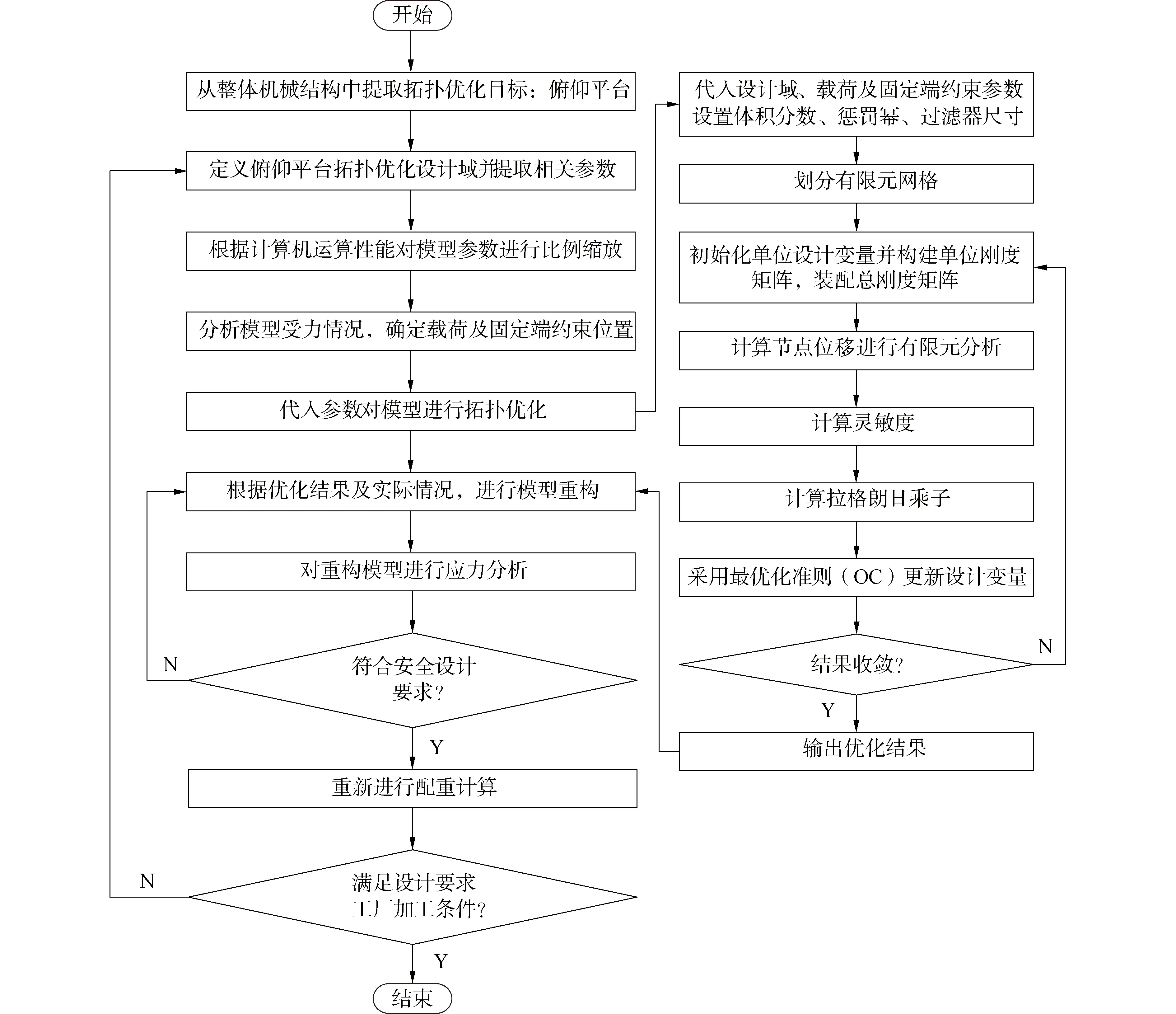
图4 激光追踪测量系统机械结构优化流程图Fig.4 Flow chart of mechanical structure optimization of laser tracking measurement system
首先提取俯仰平台中的俯仰架与连接板的相关模型参数。并指定俯仰平台连接板、俯仰架前半部分作为优化域。根据参数及模型受力情况,调整三维拓扑优化代码,对模型进行优化。为了实现三维板状结构的优化,将俯仰架拆分成前板、安装电机侧侧板及未安装电机侧侧板三部分进行优化。按照优化结果进行模型重构,并对重构模型进行应力分析。若重构模型符合安全设计标准,则继续进行配重计算;不符合安全设计准,则重新进行模型重构。最后分析配重计算结果,若满足设计要求,则优化结束;若不满足设计要求,则重新选取优化域进行优化。
3 激光追踪测量系统俯仰平台机械结构拓扑优化分析
3.1 激光追踪测量系统俯仰平台受力情况
俯仰架及连接板受力分析如图5~8所示。
在整个俯仰平台平衡中,俯仰架侧板起到杠杆的作用,即以中间部分固定端为界限。选定俯仰架两侧板的优化域为前半段;俯仰架前板和连接板的优化域为整体。图5为俯仰架前板受力图,俯仰架前板所受载荷来自于连接板及激光头,其固定约束为与两侧板连接的位置。
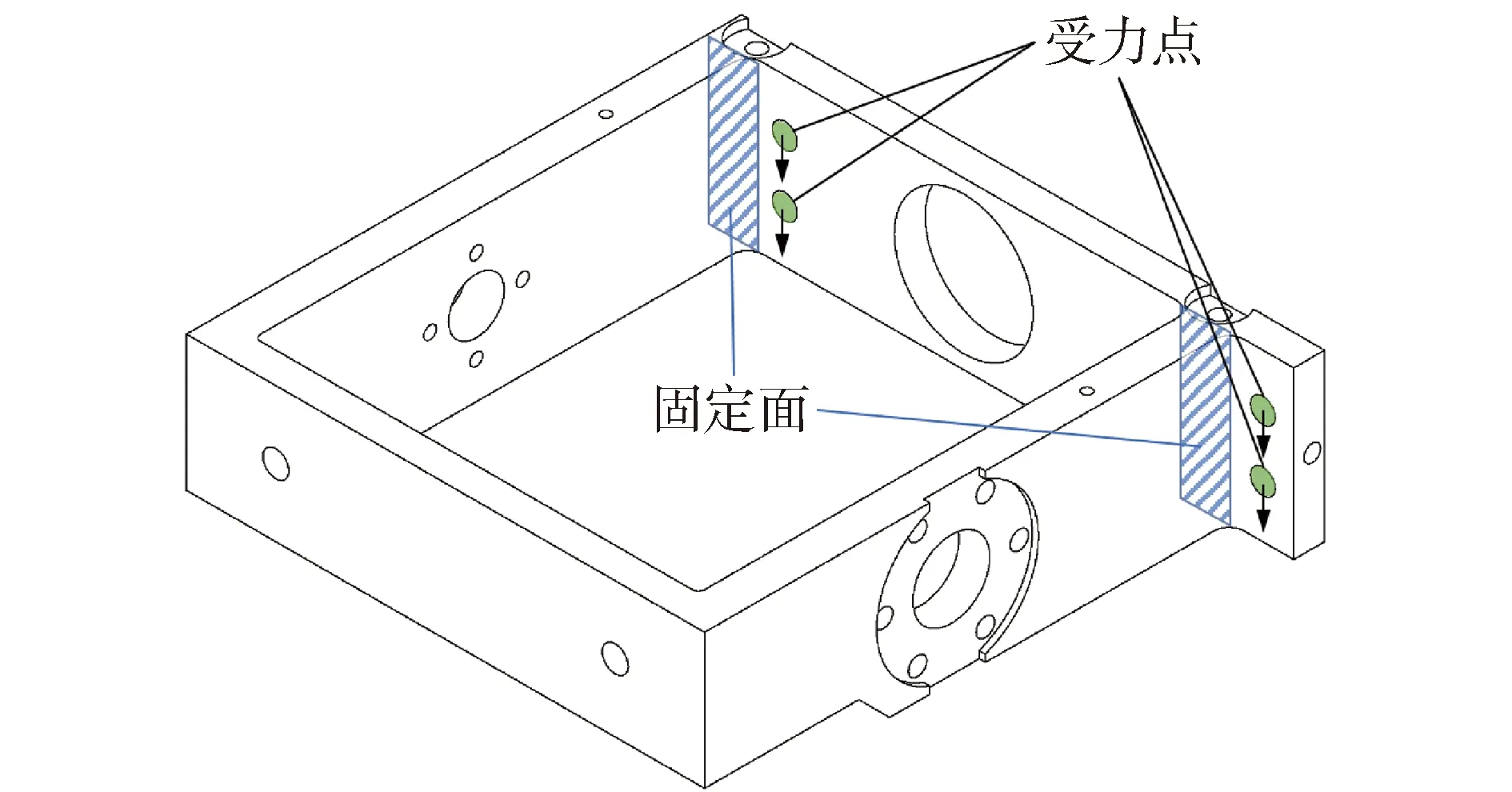
图5 俯仰架前板受力图Fig.5 Force diagram of front plate of pitch frame

图6 俯仰架安装电机侧侧板受力图Fig.6 Force diagram of side plate with motor of pitch frame

注:Fw为原配重对俯仰架施加的重力,FL为原激光头及连接板对俯仰架板加的重力图7 俯仰架不安装电机侧侧板受力图Fig.7 Force diagram of side plate without motor of pitch frame
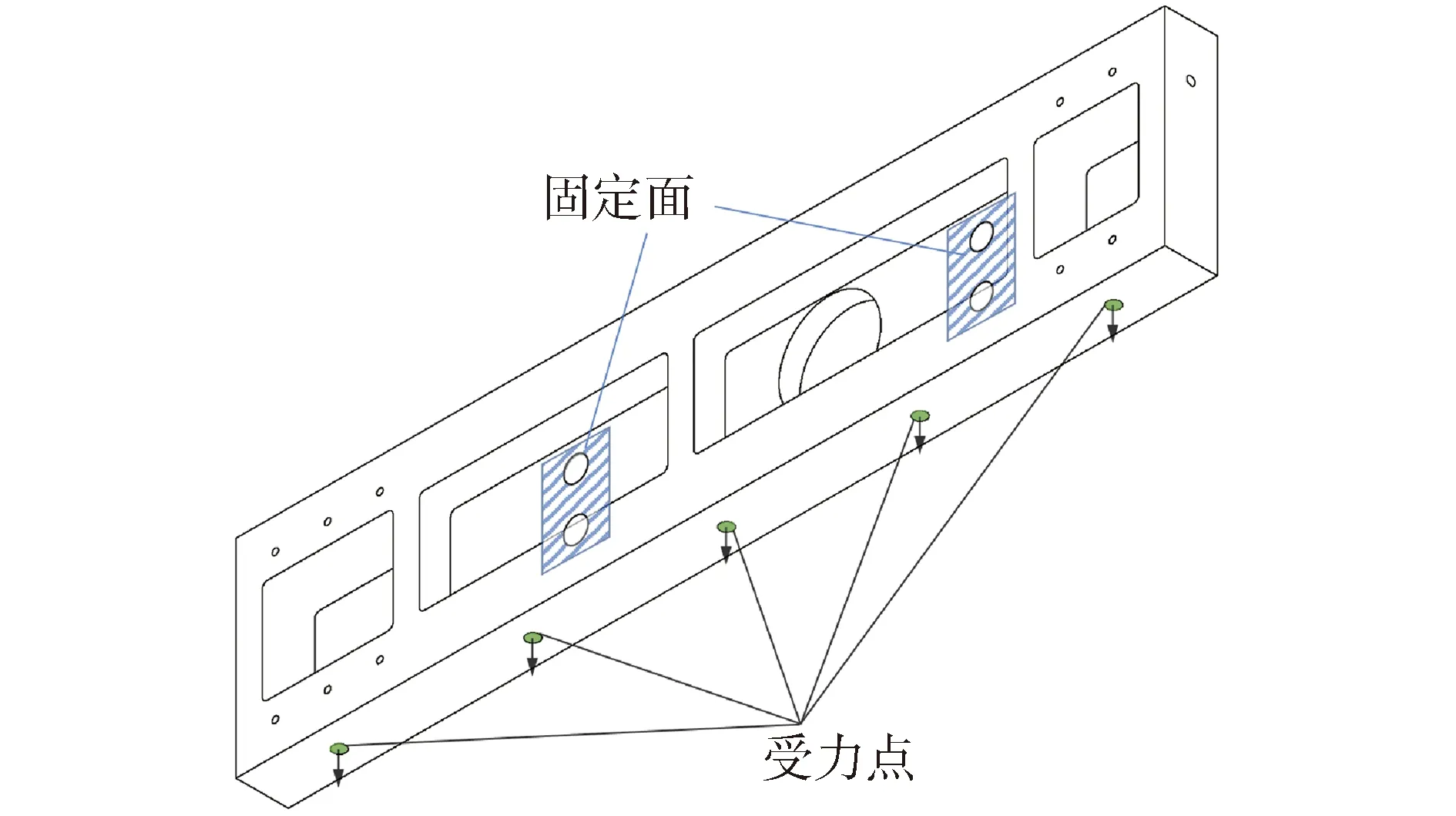
图8 连接板受力图Fig.8 Force diagram of connecting plate
3.2 激光追踪测量系统俯仰平台三维拓扑优化方法
由Inventor仿真获得俯仰平台的优化参数。根据上述参数进行初始化,对俯仰架及连接板设定的优化域进行优化。
根据文献[17]代码中所提及的优化模型,即设置材料相对密度x作为设计变量,在规定的约束和荷载条件下,优化模型结构使变形最小。建立目标为:
(4)
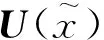
建立模型后,进行有限元分析,计算目标函数灵敏度,用OC优化准则进行设计变量更新,设置迭代次数200次。
设置体积分数0.3,惩罚功率3,滤波器尺寸1.5。优化结果如图9~11所示,优化结果边界清晰,参数设置合理。
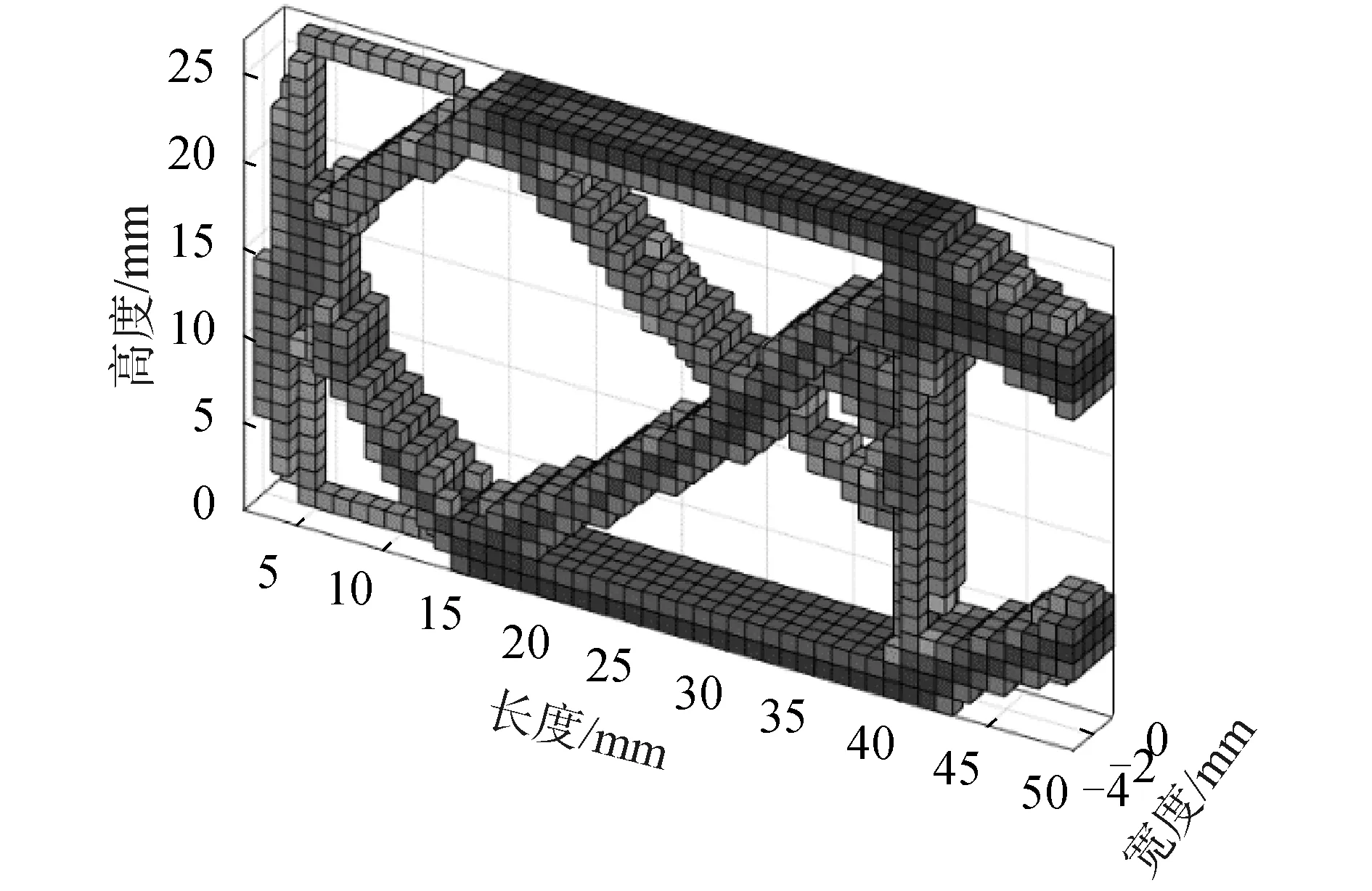
图9 俯仰架安装电机侧侧板优化图Fig.9 Topology optimization result of side plate with motor of pitch frame
图9、10分别为俯仰架安装电机侧侧板及不安装电机侧侧板优化图,优化域中心区域可去除的材料相对较多,并采用交叉支撑以减少材料的使用,得到空间最合理的布局。
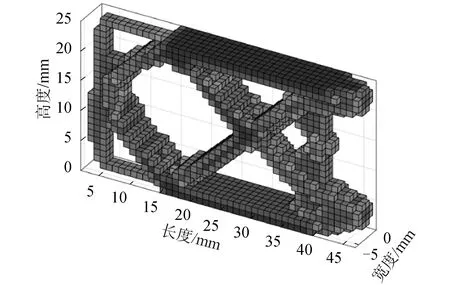
图10 俯仰架不安装电机侧侧板优化图Fig.10 Topology optimization result of side plate without motor of pitch frame
图11为连接板优化图,由于其所受载荷均在优化域底部,因此上半部分材料去除较多,但结合实际情况重构建模时要对优化结果进行适当修改,增加上半部分的支撑结构。其中因其固定形式与其他零件略有不同。图中矩形部分为夹紧块所产生的固定约束,非可减重部分。

图11 连接板优化图Fig.11 Topology optimization result of connecting plate
3.3 激光追踪测量系统俯仰平台重构模型及应力分析
根据拓扑优化结果及实际情况对模型进行重构建模,其中对俯仰架采用圆形减重孔减重方案,如图12所示;连接板重构模型如图13所示。减重后,将重构模型导入Inventor进行应力分析。俯仰架所受载荷为53 N,得到安全系数云图如图14所示,可知重构模型的安全系数均大于15,即轻量化后的机械结构可以安全承受所加载荷,满足设计要求。
周一,美国市场开市,中国还是假期,看到了雷曼破产,中投风控部工作人员,挨个打电话给自己的分布在全球的投资经理,尤其是帮助中投管理货币市场基金的经理,询问在他们的投资组合里,是否有雷曼的债券?果然,Primary的基金经理回复,他们资产池中有4%的仓位在雷曼债券上。该基金全称Reserve Primary Fund,在其持有人名单上,中投公司旗下的Stable Investment是最大持有人,持有份额折合市值约54亿美元。
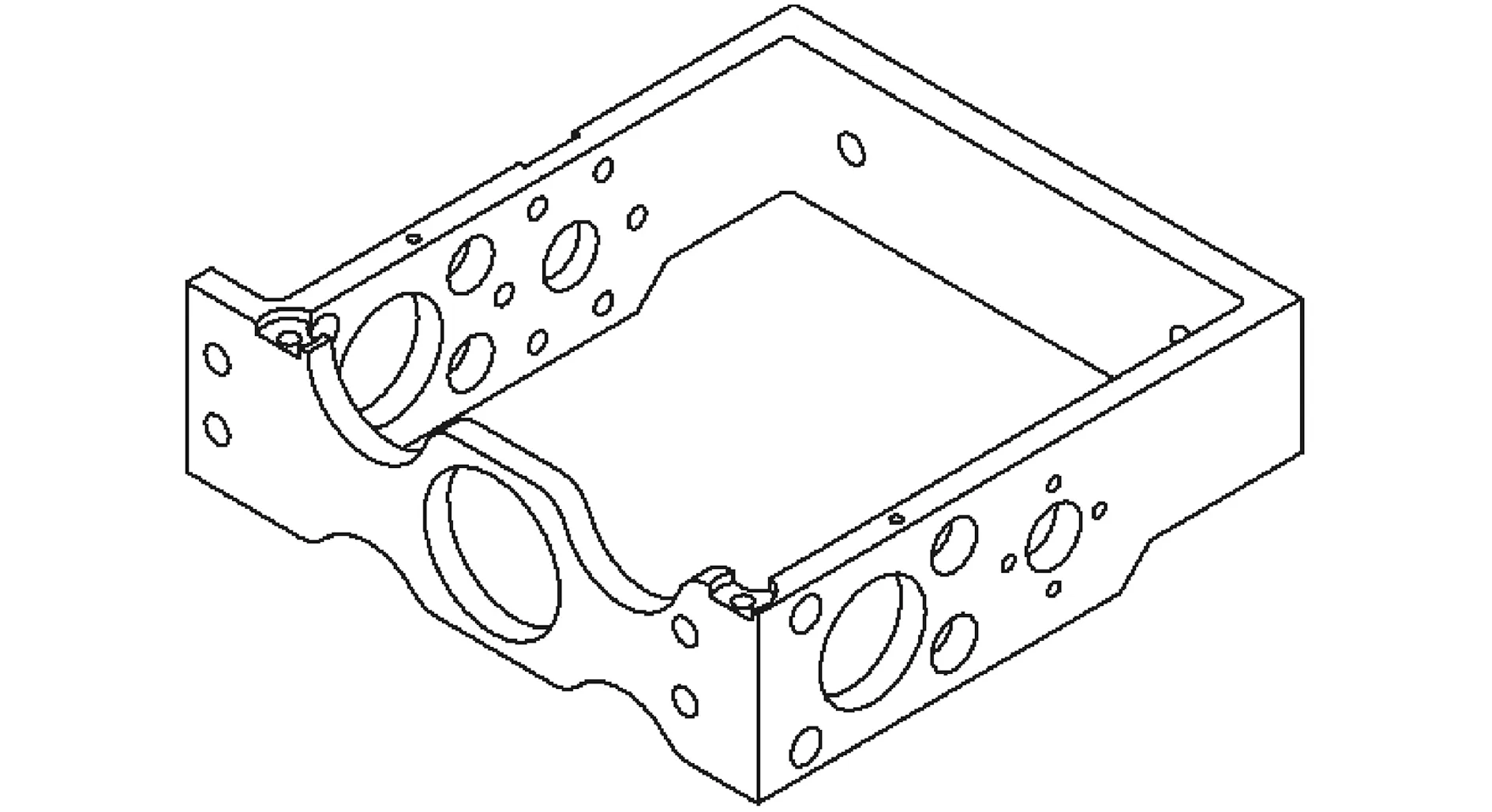
图12 圆形减重孔俯仰架结构Fig.12 The structure of round weight-reducing hole pitch frame
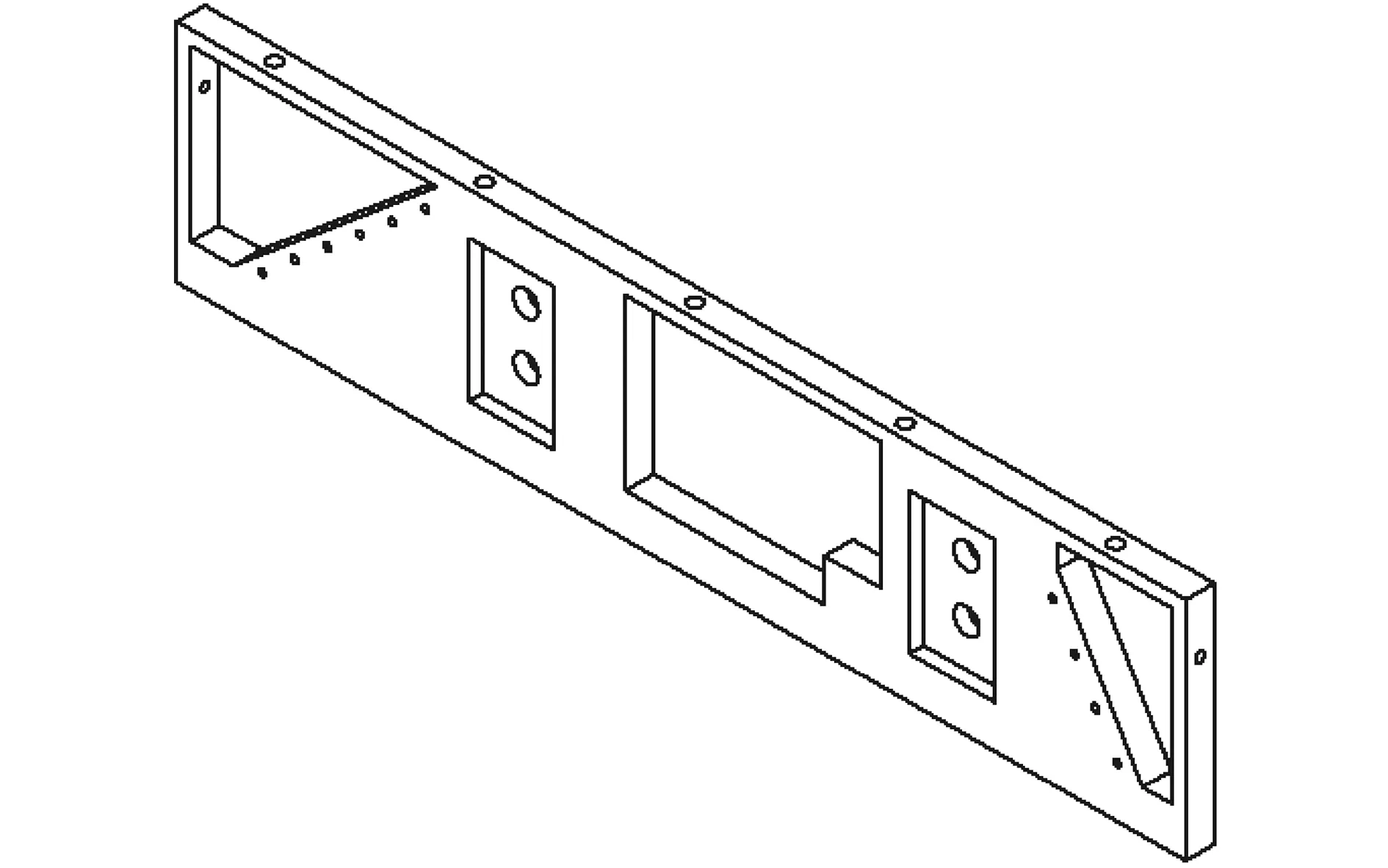
图13 连接板结构Fig.13 The structure of connecting plate
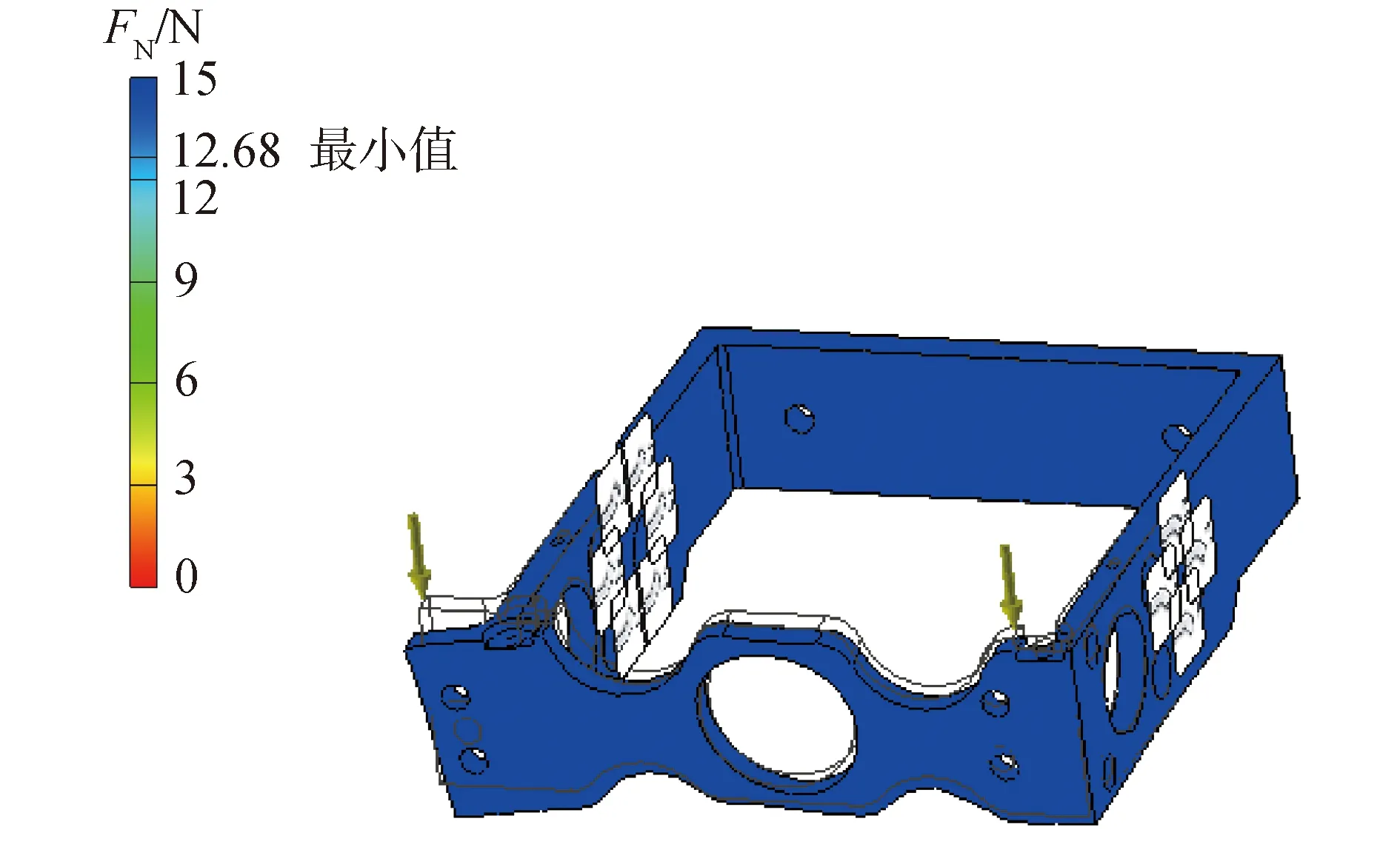
图14 圆形减重孔俯仰架应力云图Fig.14 Stress analysis diagram of round weight-reducing hole pitch frame
同理,连接板应力分析云图如图15所示,连接板所受载荷为22 N,其安全系数大于15,轻量化后的机械结构可以安全承受所加载荷,满足设计要求。

图15 连接板应力云图Fig.15 Stress analysis diagram of connecting plate
3.4 激光追踪测量系统配重计算
为了检验轻量化方法的实际应用价值,计算减重后的俯仰平台所需配重的质量,检验其是否小于原配重质量。
在不添加配重的情况下,由于激光跟踪系统激光头部分(俯仰模块)的质心会与俯仰电机的旋转轴线产生一个偏心距,增加了俯仰电机的高速伺服控制难度,使其难以将电机控制参数调整到一个合适的数值。因此在俯仰架尾端添加配重可以达到与前端激光头平衡,通过杠杆平衡的原理,获得所需配重质量。
如图16所示,分别以标准球球心为原点O,水平回转轴、垂直回转轴为X轴和Z轴,建立O-XYZ坐标系。以XOZ平面为分割面,将整个俯仰平台分为如上文所述的前半部及后半部。设水平回转前半部质心点空间坐标为A(x1,y1,z1),标准球球心为空间坐标系原点O(0,0,0),水平回转后半部质心点空间坐标为B(x2,y2,z2),尾架部分质心点空间坐标为C(x3,y3,z3),配重块质心点空间坐标为D(x4,y4,z4)。设俯仰前半部质量为m1,尾架部分质量为m2,配重块质量为m3,水平回转后半部质量为 (m2+m3)。
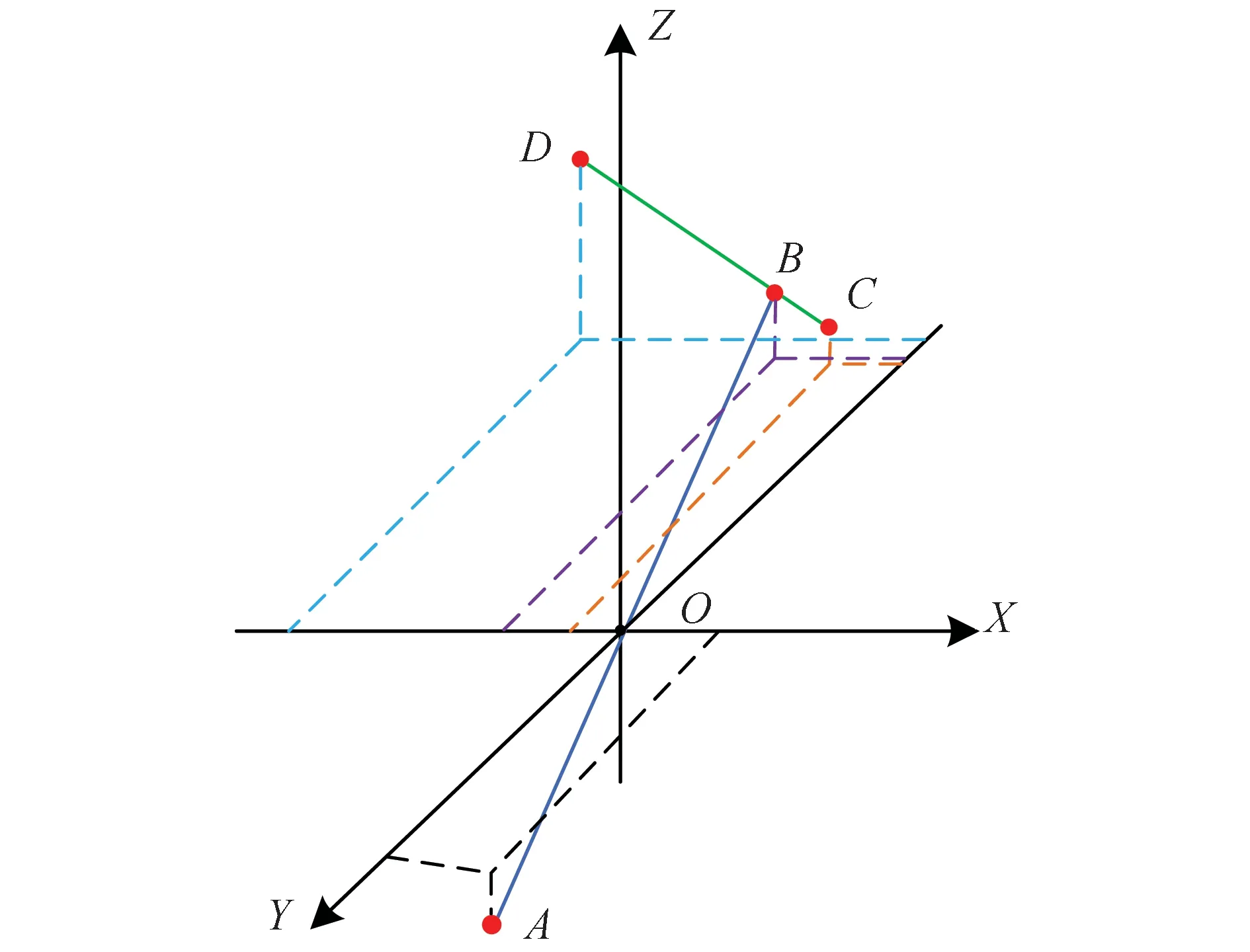
图16 俯仰平台质心分布Fig.16 Centroid distribution of pitch frame
以AB为杠杆,原点O为杠杆支撑点,满足方程:
m1·|AO|=(m2+m3)·|OB|
(5)
则AO的直线方程与∣AO∣、∣OB∣的长度可以表示为:
(6)
(7)
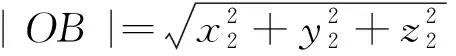
(8)
质心点B为质心点C与质心点D的合成质心点,且质心点B位于AO直线延长线上。则合成质心点B的空间坐标方程为:
(9)
将∣AO∣长度式(7)与∣OB∣长度式(8)代入杠杆定理方程(5)后得到方程:
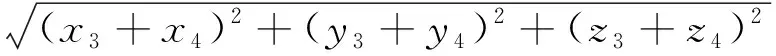
(10)
根据方程(10)获得配重质量m3。
基于上述模型,对俯仰平台实现平衡所需配重进行计算,对于优化前的俯仰平台实现平衡所需配重质量为7.77 kg(材料:硬质合金,密度:15.50 g/cm3)。
根据本文提出的三维拓扑方法对激光追踪系统机械结构进行轻量化后,计算得到的所需配重质量为4.64 kg。相比优化前实现平衡所需的配重质量减少了3.13 kg。
4 结论
1)采用三维拓扑优化算法对激光追踪测量系统俯仰平台的连接板和俯仰架进行轻量化设计,得到满足系统结构强度与系统安全系数要求的轻量化连接板与俯仰架模型。相较轻量化优化前,连扳优化后直接减重1.65 kg,减重效果达55.7%;俯仰架优化后直接减重0.628 kg,减重效果可达27.9%。
2)在保证传力效果和传力路径的基础上,对类板状拼接型零件进行拆解分块分析。该方法既解决了复杂类板状拼接型零件难以设定受力的问题,又可以保证优化结果的准确性。
3)本文通过拓扑优化对激光追踪测量系统关键零件轻量化,在不改变零件原设计整体结构的情况下,实现在有限体积内配重质量达到设计要求的目的。
4)本文将拓扑优化技术引入到激光追踪测量系统结构设计中,降低了常规设计方法中的局限性,提高了激光追踪测量系统设计效率,是对激光追踪测量系统设计方法的补充和改善,具有参考意义。
