能量空间裂纹转子振动特性与诊断研究
2022-03-11刘军张宇汪畅张冕
刘军, 张宇, 汪畅, 张冕
(1.天津市先进机电系统设计与智能控制重点实验室, 天津 300384;2.机电工程国家级实验教学示范中心(天津理工大学), 天津 300384)
高速旋转机械在工业生产中有着举足轻重的地位,而转子作为旋转机械的重要组成部分,往往工作在恶劣的条件下,加之运行时所受到的周期性交变载荷及转子本身的材料缺陷,容易伴随着裂纹的萌生与扩展,若不及时发现,会造成转子的断裂或系统运行停止等损失,严重了甚至会危及生命。多年前,裂纹转子动力学特性吸引了国内外研究者的广泛关注,针对裂纹转子数学模型的构建、裂纹转子系统的振动特性分析和裂纹诊断等开展了大量的研究,形成了较为完善的裂纹转子理论体系。
Arem等[1]采用简化裂纹数学模型,将裂纹简化成2个由集中质量非线性弯曲弹簧连接的无裂纹刚性杆模型,并进行了理论分析。Shudeifat等[2]以裂纹转子系统为研究对象,基于单位时变刚度矩阵等特征,对时变刚度裂纹转子的动力学特性进行分析。Liu 等[3]利用开闭映射法研究了转速、不均匀质量、扁平性等参数对裂纹开闭特性的影响。Xiang等[4]综合考虑裂纹和碰摩等故障和油膜支撑的非线性,着重研究了耦合故障的转子模型涡动轨迹特征及各故障之间的耦合效应。Hamid等[5]讨论了2个裂纹同时存在时裂纹深度、位置和相对角位置等特征对系统振动特性的影响。Anuj等[6]建立了含有非对称项的多转子系统的动态数学模型,研究了非对称刚度对多转子系统参数不稳定性的影响。Shudeifat等[7]分析了连续加速和减速2种瞬态情况下裂纹对转子系统前向进动与后向进动的影响。Cavalini等[8]以双转子为研究对象,通过理论分析,对含裂纹转轴的非线性振动进行了研究。Hou等[9]以裂纹转子系统为研究对象,研究了1/2和1/3亚谐波共振的局部分岔特性,讨论了模态特性和裂纹呼吸对系统动态响应的影响。
在裂纹故障诊断及监测方面,主要有基于动力学模型和响应信号的2种方式[10]进行诊断。Chandra等[11]比较了短时傅立叶变换(STFT)、连续小波变换(CWT)和希尔伯特-黄变换(HHT)3种信号处理工具的检测性能。Liu等[12]利用HHT能量谱分析在裂纹转子的瞬态振动信号下研究了裂纹故障诊断,通过理论分析与实验验证发现该方法在早期裂纹信号检测上优于小波分析方法。Liu等[13]基于非线性输出频率响应函数,提出了一种转子裂纹检测与量化准则,放大转子振动特性对裂纹的敏感影响。Rodrigo等[14]采用近似熵算法,对模拟得到的裂纹信号,实现了转轴的裂纹检测。目前,鲜有文献从能量观点对裂纹转子振动特性及裂纹诊断进行分析和研究。Liu等[15]引入能量轨道迁移、能量Poincare映射、能量轨迹稳定性和能量供给函数等概念,分析了双转子系统的非线性振动特性。但是,该研究并未对裂纹转子进行系统分析。
针对研究中存在的上述问题,基于振动能量空间,本文提出了振动能量分析方法,并与相空间分析相结合,研究了不同临界转速区域在能量空间的转子振动特性,转子系统不同参数对非线性振动特性及振动能量轨道变化规律的影响;基于提出能量轨道、能量FFT和能量轨道畸变等概念,研究不同裂纹和非线性等参数对系统振动特性的影响,相关实验验证了裂纹转子的能量FFT和轨道畸变。研究结果表明能量FFT和能量轨道畸变规律能够更适合诊断转子的裂纹故障,为分析裂纹转子系统振动响应和故障诊断提供了一种方法。
1 裂纹转子模型及动力学方程
为体现提出方法的可行性,选用Jeffcott模型,并取裂纹靠近圆盘附近,裂纹最大深度为a,圆盘质量偏心e。当转轴一端支撑选用单列深沟球轴承时,转子支撑恢复力会出现复杂的非线性项[16],并引起系统非线性振动现象。
1.1 转子系统的数学模型
转子模型如图1,并导入直角坐标系O-XYZ。由于转子系统水平放置,在重力的作用下,x方向会产生一定程度的挠曲变形r。
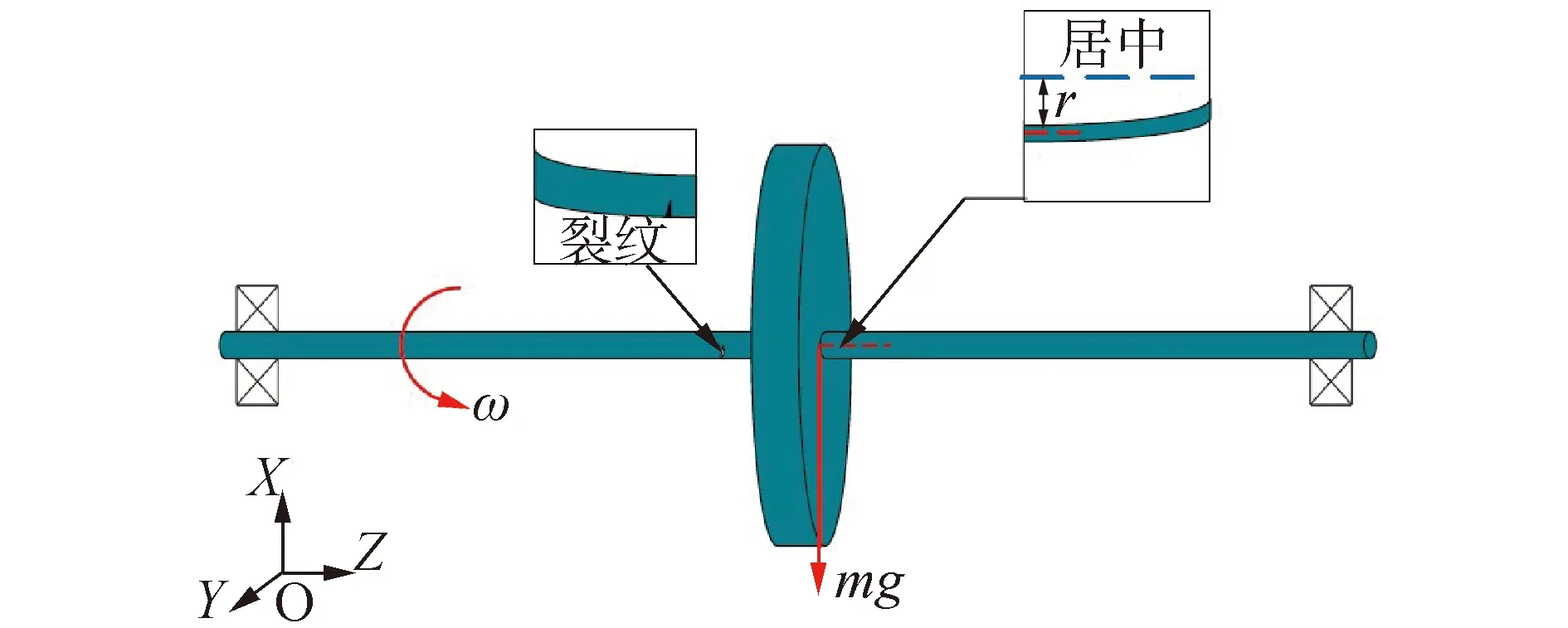
图1 裂纹转子模型Fig.1 Cracked rotor model
转子系统的动力学方程表示为:
(1)
式中:m为圆盘质量;c为阻尼系数;k为无裂纹弹性转子系统的刚度系数;ω为旋转速度;φ为不平衡方向初始相位角。
1.2 裂纹转子的刚度模型
裂纹参数在转子坐标系的关系如图2所示,重力作用下转子产生弯曲变形,会影响裂纹开闭。
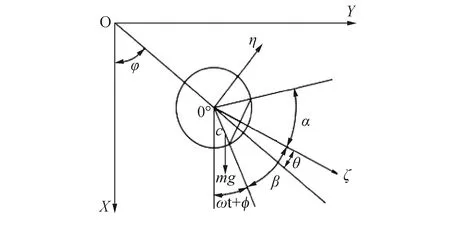
图2 裂纹参数在转子坐标系的关系Fig.2 Relationship of crack parameters in coordinate system
设裂纹位置设定靠近圆盘,且裂纹张开角度充分,在旋转坐标系中,随着裂纹张开,裂纹方向的刚度值会大大降低,即刚度变化主要体现在ξ方向的刚度变化量Δk,η方向的刚度变化量影响较小可忽略不计。故裂纹的刚度矩阵方程可表示为:
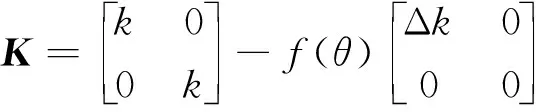
(2)
式中f(θ)为裂纹开闭函数。
1.3 裂纹模型
裂纹模型要反映裂纹在转子运行中全开、全闭及变化过程,并保持各过程中合理的持续时间。在此选用裂纹混合模型,其函数表达式[17]:
(3)
式中:θ=ωt+φ+β-φ,α为裂纹张开角度的一半。
1.4 非线性弹簧恢复力数学模型
当转轴一端支撑使用单列深沟球轴承时,由于内环对滚珠运动限制,支撑恢复力会产生特性不同的非线性项,其恢复力引起的能量方程为:
β40x4+β31x3y1+β22x2y2+β13x1y3+β04y4
(4)
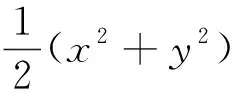
通过能量方程(4)对x与y方向的导数,得出转子系统的非线性项表达式[16]表示为:
(5)
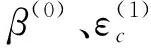
1.5 无量纲非线性裂纹转子动力学方程
为了计算及研究方便,对转子动力学方程(1)进行无量纲处理,变换参数为:
变量无量纲处理后,为简化将各变量上标“-”省略,并将式(2)、(3)和(5)导入,裂纹转子系统的动力学方程为:
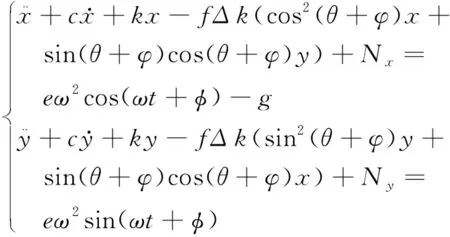
(6)
2 相空间与能量空间中振动特性分析
2.1 转子的振动特性理论解的诱导
设该系统的动力学方程解表示为:
(7)
基于谐波平衡法,利用Mathematics代入系统动力学方程(6),经过三角函数简化整理得到:
(8)
式中:f1、f2为常数项系数;f3、f4为ω成分系数,f5、f6为ω/2成分系数。
2.2 线性裂纹转子的振动能量特性分析
将裂纹转子在旋转坐标系中的刚度矩阵式(2)代入势量方程V=kx2/2,可得到其在旋转坐标中的能量方程为:
(9)
将式(9)转化到直角坐标系中,可得到裂纹转子系统在直角坐标系下的能量方程:
(10)
基于式(10),通过数值仿真,做出该系统振动能量变化的时间历程图、能量FFT图、能量庞加莱图以及能量轨道图,分析振动能量随时间的变化关系、分析能量成分、能量的变化周期以及阐述能量轨道的变化规律,以上称作在振动能量空间中对系统的振动特性分析,即在振动能量空间中基于能量变化规律解释裂纹转子的振动特性。
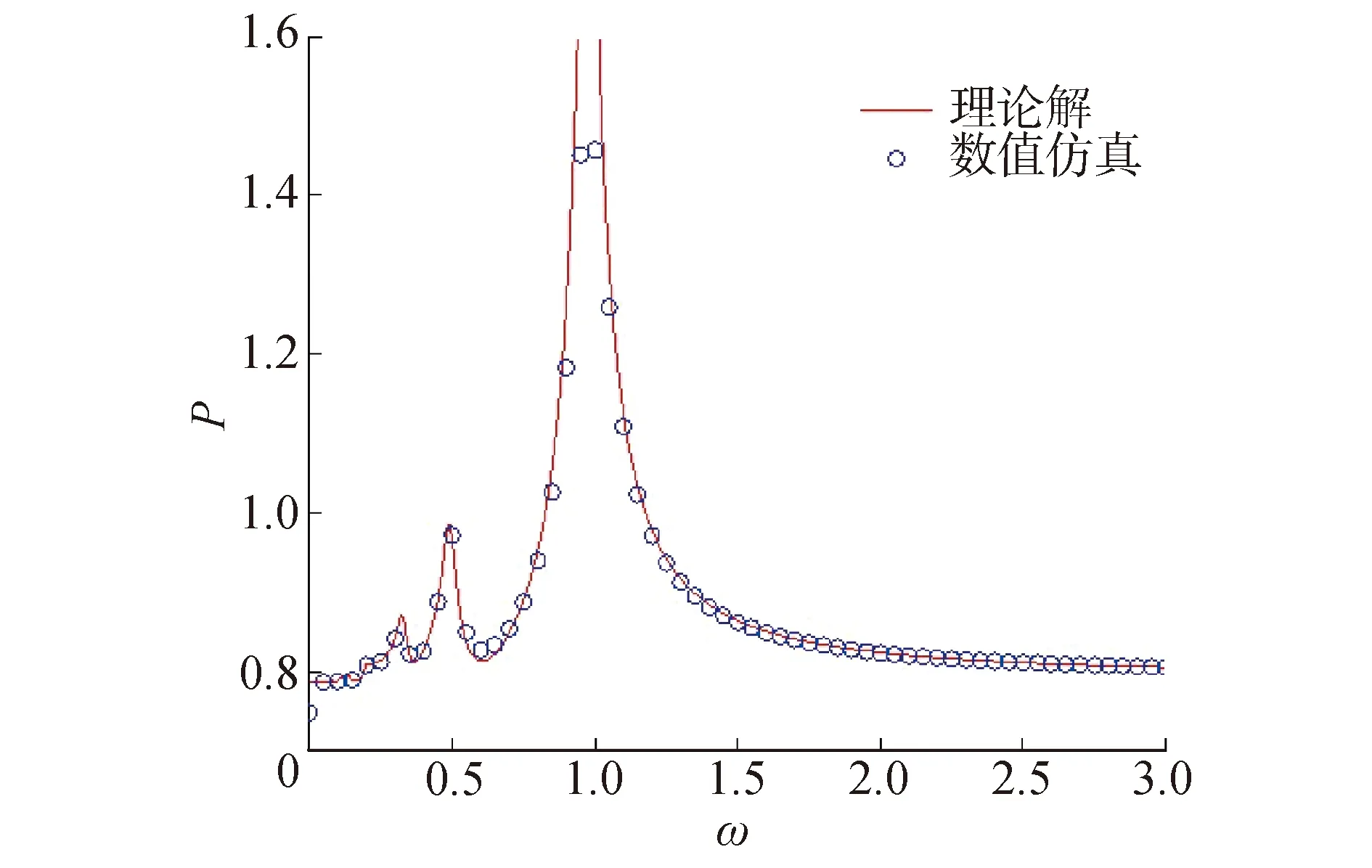
图3 裂纹转子振动响应曲线(线性)Fig.3 Vibration response curve of the linear cracked rotor
在ω=0.49时能量空间中的时间历程图、频谱图、庞加莱映射图及能量轨道,如图4所示。图4(a)和4(b)为超谐波共振时振动能量变化的时间历程和庞加莱映射图,表明了裂纹转子的振动特性变化规律。图4(a)能量变化值出现2种成分的周期振动,图4(b)能量庞加莱映射中2点落在能量轨迹平面上,即此时转子振动能量呈二倍周期规律变化。图4(c)表示能量频谱图,结果可以分析出,转子在振动过程中,能量变化的主要频率为ω和2ω成分。图4(d)为转子能量在x-y方向的投影轨道变化。
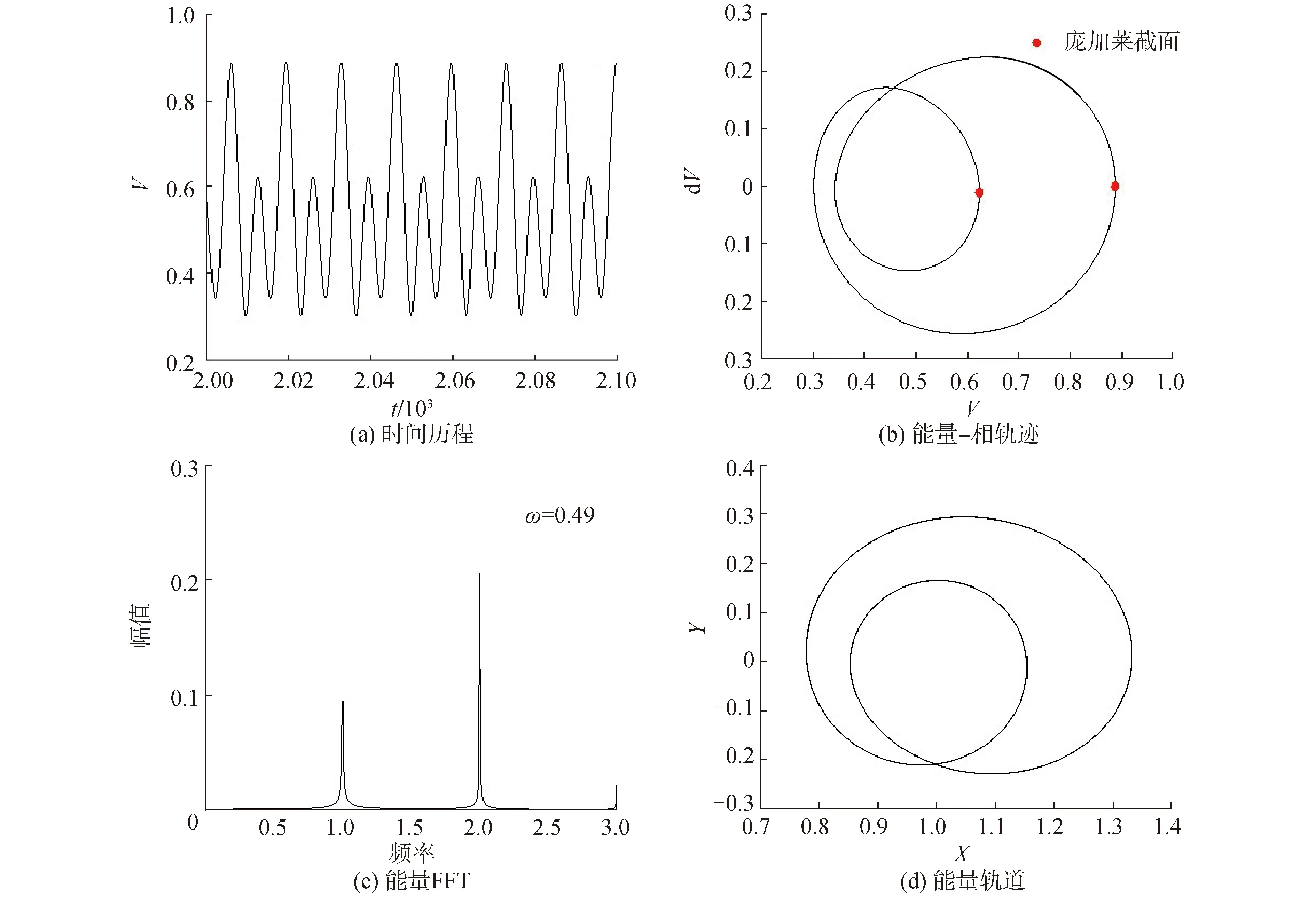
图4 能量空间特性分析(超谐波共振)Fig.4 Analyses of energy change characteristics in the vicinity of the secondary critical speed
在ω=0.99附近时能量变化的时间历程图、频谱图、庞加莱映射图及能量轨迹图,如图5所示。图5(a)和5(b) 表示主谐波共振附近振动能量的时间历程和庞加莱映射图。图5(a)显示能量变化为单周期变化,图5(b)表示庞加莱映射一点落在能量轨迹平面上,即转子在振动时能量呈单周期规律变化。图5(c)为能量频谱图,分析得到振动能量频率变化主要为ω成分,并且出现了很小的2ω成分。图5(d)为转子的振动能量轨道在x-y方向的投影轨迹变化。基于振动能量频谱和轨道分析,在一定程度上能清晰的反映出裂纹的影响。
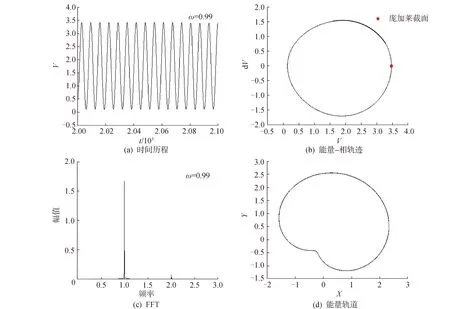
图5 主谐波共振能量变化特性分析(线性)Fig.5 Analyses of energy change characteristics in the vicinity of the major critical speed (linear)
2.3 非线性裂纹转子的能量特性分析
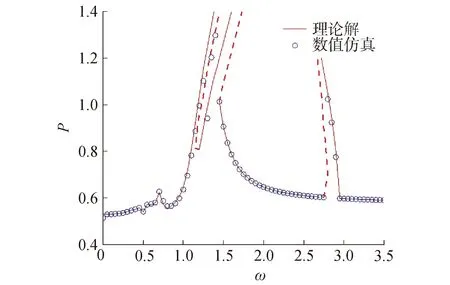
图6 非线性裂纹转子振动响应曲线Fig.6 Vibration response curves of the nonlinear cracked rotor
在ω=0.68超谐波共振附近,图7(a) 和7(b)为振动能量变化的时间历程和庞加莱映射图。图7(a)显示能量变化出现2种不同频率的周期振动,图7(b)中庞加莱映射有2点落在能量轨迹平面上,即转子的振动能量呈二倍周期规律变化。图7(c)为能量频谱图,分析得到系统的振动能量频率主要为ω和2ω成分,还有很小的3ω成分。图7(d)为转子能量轨道在x-y方向的投影轨迹,突显非线性的影响。

图7 超谐波共振能量变化特性分析Fig.7 Analyses of energy change characteristics in the vicinity of the secondary critical speed
在ω=1.26主谐波共振附近,图8(a)和8(b)为振动能量变化的时间历程和庞加莱映射图。分析可知,图8(a)振动能量的变化已经不再是简单的单周期振动。图8(b)中庞加莱映射为有2点落在能量轨迹平面上。图8(c)显示振动能量频谱图,振动能量的主要频率是ω和2ω成分,3ω成分也十分明显。图8(d)表示转子能量轨道在x-y方向的投影轨迹,显不规则椭圆型。
在ω=2.83 1/2次亚谐波共振附近,图9(a)和9(b) 为振动能量变化的时间历程和庞加莱映射图。分析可知,图9(a)振动能量变化显示为二倍周期变化,图9(b)中庞加莱映射为两点落在能量轨迹平面上,与图9(a)相对应。图9(c)显示振动能量频谱图,出现了明显的1/2ω、ω和3/2ω成分,很小的2ω成分。图9(d)表示转子振动能量轨道在x-y方向的投影轨迹,显不规则轨迹。
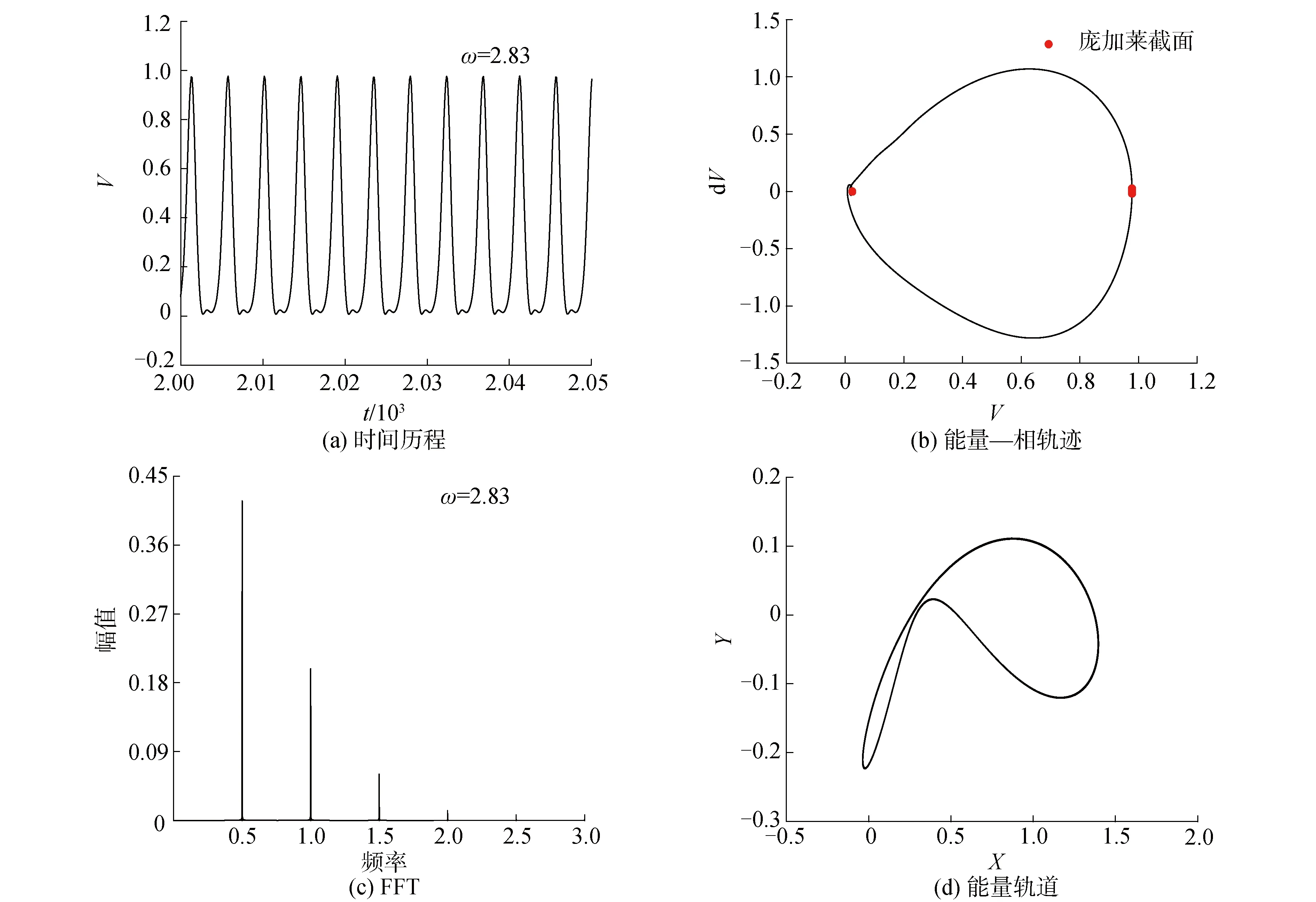
图9 1/2次亚谐波能量变化特性分析Fig.9 Analyses of energy change characteristics in the vicinity of the subharmonic of order 1/2 critical speed
通过振动能量空间分析结果分析可知,不同区域能量频谱分析在一定程度上加强了超谐波成份,2ω成份更加显著。
2.4 裂纹转子的相频谱与能量频谱对比
由于裂纹检测的一个重要标识在于振动特征的变化,如果能在高转速区发现超谐波成份,有利于裂纹检测。基于上述分析,无论是在主谐波共振附近或是1/2次亚谐波共振附近,能量频谱中的超谐波成分都比相空间振动信号分析更加明显。变化不同裂纹深度、相对位置及非线性系数等参数时,振动频谱与振动能量频谱对比及分析证明该观点。
2.4.1 裂纹深度的变化
取不同Δk值表示裂纹深度的变化。裂纹深度变化时,非线性裂纹转子系统的振动响应曲线,如图10所示。随着裂纹加深,无论是在1/2次亚谐波共振和主谐波共振附近,振幅值都相对增加,主谐波附近会出现解的分化和下沉,如同图6所示的变化。1/2次亚谐波共振会向高速方向推移。在主谐波共振附近以转速ω=1.26时得到的振动与振动能量频谱图,如图11所示。随着裂纹的加深,图11(a)中ω成分略有升高,而2ω成分几乎不可见。而图11(b)中,随着裂纹的加深,除ω成分略升高外,还可以看到明显的2ω成分,并出现3ω成分。在1/2次亚谐波共振附近ω=2.83时得到的振动与振动能量频谱图,如图12所示。随着裂纹的加深,图12(a)中ω成分略有升高,而图12(b)与图12(a)相比,同样2ω成分更加明显,并出现3ω成分。
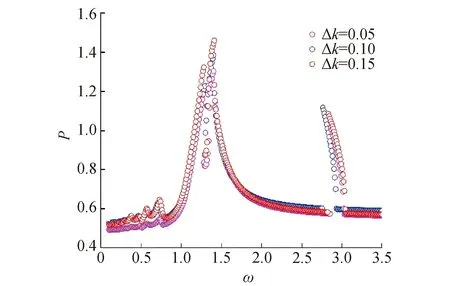
图10 不同裂纹深度振动响应曲线Fig.10 Vibration response curves under different crack depths
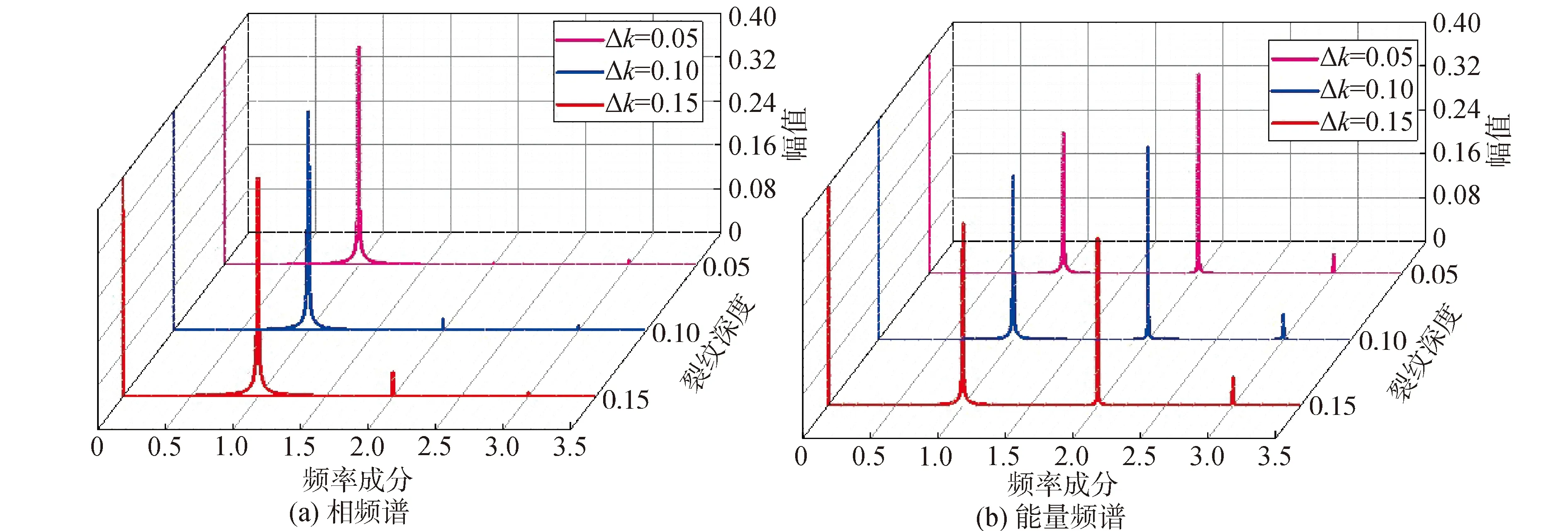
图11 主谐波共振随着裂纹加深的频谱分析Fig.11 Frequency spectrum analyses with crack depths in the vicinity of the major critical speed
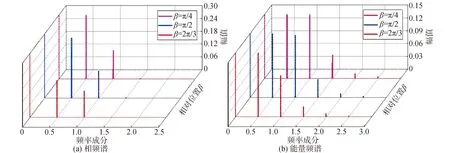
图12 1/2次亚谐波随着裂纹加深的频谱分析Fig.12 Frequency spectrum analyses with crack depths in the vicinity of the subharmonic of order 1/2 critical speed
2.4.2 裂纹与偏心位置的变化
随着裂纹与质量偏心的相对位置β角的增加,在主谐波共振ω=1.26附近的振动与振动能量频谱图,如图13所示。随着β角的增加,图13(a)中ω成分略有降低,而2ω成分几乎不可见。图13(b) 中,除ω成分略有降低,还可以看到明显的2ω成分,并出现3ω成分。在1/2次亚谐波共振附近ω=2.83时得到的振动与振动能量频谱图,如图14所示。随着β的增加,图14(a)中1/2ω成分保持,ω成分略有降低。图14(b)与图14(a)相比,3/2ω和2ω成分明显。
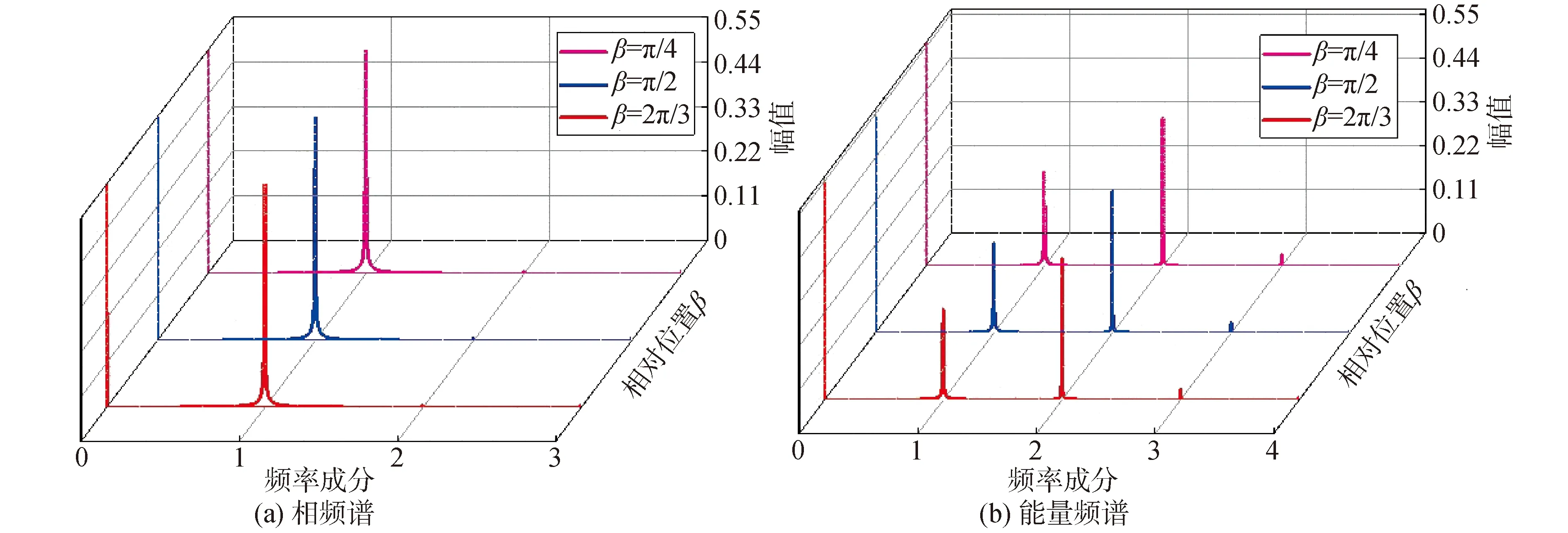
图13 主谐波共振随着相对角增加的频谱分析Fig.13 Frequency analyses with the increase of relative angles in the vicinity of the major critical speed

图14 1/2次亚谐波随着相对角增加的频谱分析Fig.14 Frequency analyses with the increase of relative angles in the vicinity of the subharmonic of order 1/2 critical speed
2.4.3 非线性参数的变化
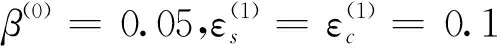
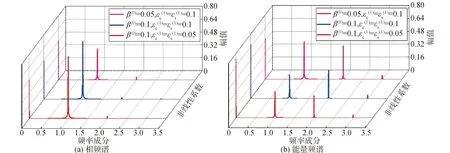
图15 主谐波共振不同非线性参数下的频谱分析Fig.15 Spectrum analyses under different nonlinearities in the vicinity of the major critical speed

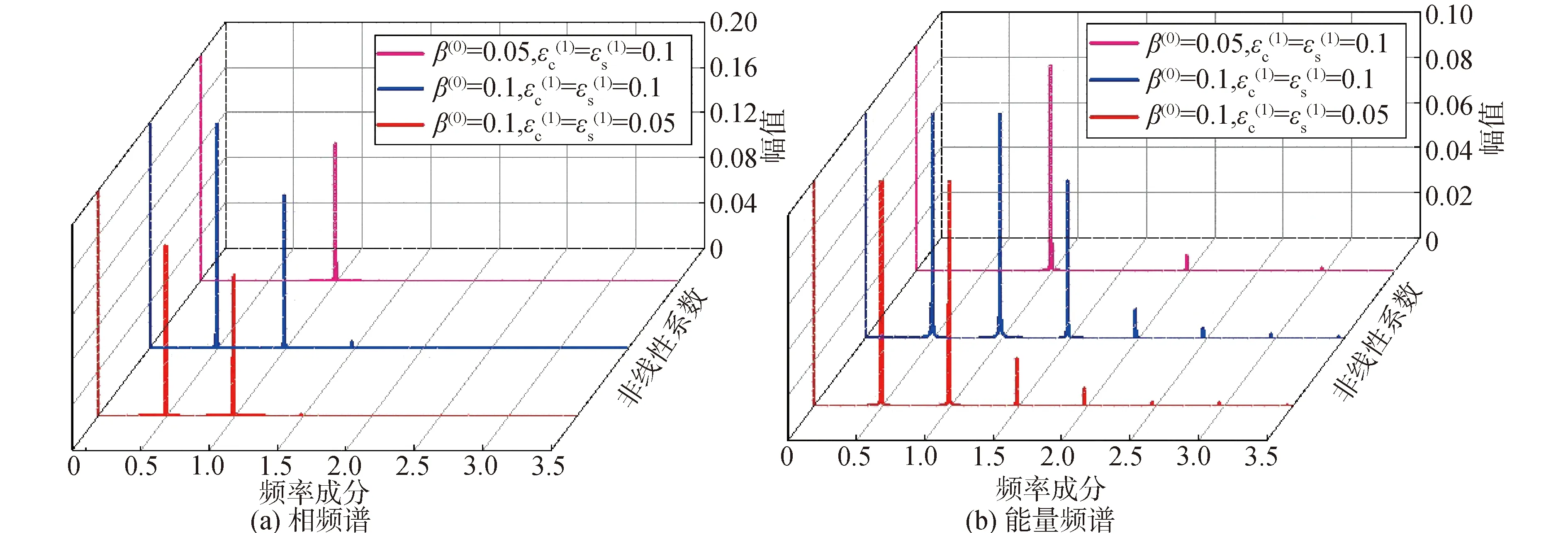
图16 1/2次亚谐波不同非线性参数下的频谱分析Fig.16 Spectrum analyses under different nonlinearities in the vicinity of the subharmonic of order 1/2 critical speed
综上,随着不同参数变化在主谐波共振及1/2次亚谐波共振附近的振动能量频谱图中可以明显的发现超谐波共振成分。
3 基于能量轨道的裂纹诊断研究
基于系统的能量空间,研究裂纹转子的能量轨道变化,找出裂纹参数影响下能量轨道的变化规律,可以完善对系统的振动特性分析及诊断。
研究能量方程(10)发现,能量V是由不同频率成分的能量叠加的结果。为了更直观的研究振动能量变化,将能量变化在三维能量空间V-X-Y中进行描点,称为振动能量轨道,其中X和Y数值序列可通过V分别在X和Y轴投影获得。
3.1 不同裂纹深度引发能量轨道变化(主谐波共振)
随着Δk的变化,主谐波共振ω=1.26附近的振动能量轨道变化,如图17所示。图17(a)为三维能量轨道。从中可分析出,裂纹轨道为两边对折的封闭曲面。裂纹的加深使得能量对折处一边升高,并向两侧倾斜膨胀,即裂纹越深,能量轨道幅值越大,振动越激烈。图17(b)为振动能量轨道在x-y方向的投影。当Δk=0.05时,投影为一个带有凹陷的椭圆;当Δk=0.1时,凹陷明显变缓,但轨道旋转并扩展;当Δk=0.15时,凹陷处轨迹更加向外扩展。
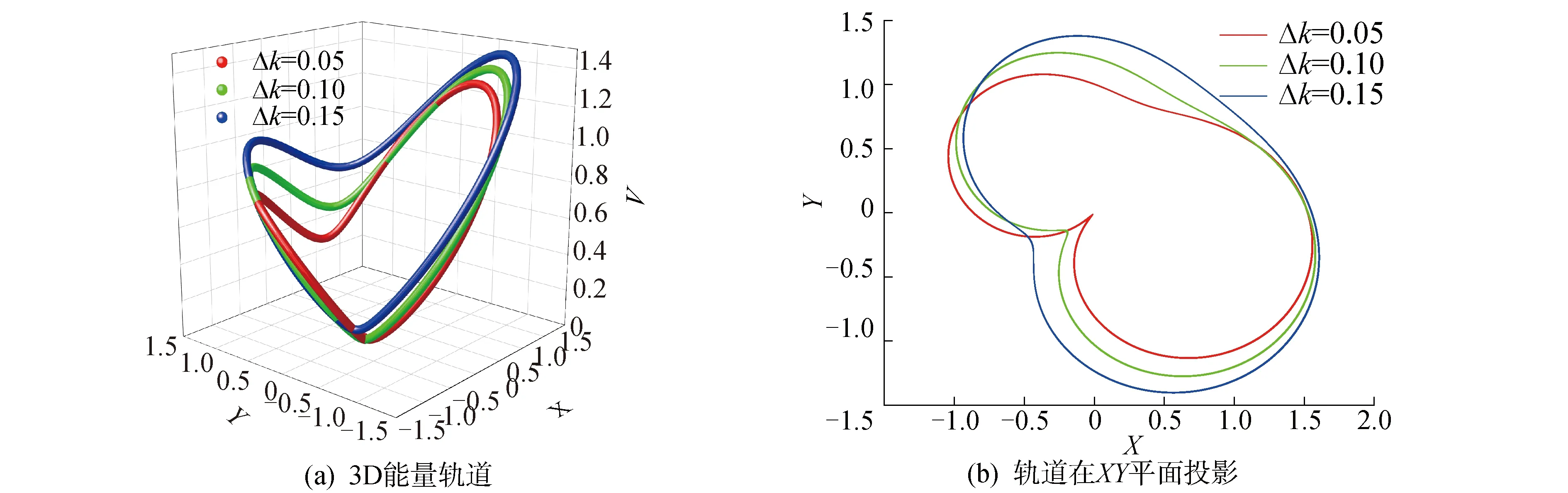
图17 主谐波共振裂纹深度对能量轨道的影响Fig.17 The influence of energy tracks with crack depths in the vicinity of the major critical speed
3.2 不同裂纹参数引发能量轨道变化(亚谐波共振)
随着Δk的变化,亚谐波共振ω=2.83附近的振动能量轨道变化,如图18所示。图18(a)为三维能量轨道。从中可分析出,裂纹轨道呈倾斜的封闭曲面。随着裂纹深度Δk的增大,曲面越倾斜,幅值也相对增加,即裂纹越深,能量轨道幅值越大。图18(b)为振动能量轨道在x-y方向的投影。当Δk=0.05时,投影为有一个凹陷的圆面;当Δk=0.1时,圆面凹陷处上方向内收缩;当Δk=0.15时凹陷处已经明显收缩为“凸”字形,这一发现可以为裂纹的检测提供新的轨道畸变依据。

图18 1/2次亚谐波裂纹深度对能量轨道的影响Fig.18 The influence of energy tracks with crack depths in the vicinity of the subharmonic of order 1/2 critical speed
3.3 实验验证
构建了实验装置,如图19所示。水平支撑且材料为不锈钢的转子系统,其长度和直径分别为700 mm和12 mm。圆盘安装在轴的中心位置,直径和厚度分别为300 mm和15 mm。采用2个激光传感器从2个正交方向测量圆盘的径向位移,得到转子系统的振动响应。转子上裂纹的制作是利用激光切割转轴1.5 mm深的细窄缝,其位置在圆盘附近。通过实验,裂纹转子系统的主谐波共振为800 r/min。

图19 实验装置Fig.19 Experimental setup
在主谐波共振附近转子系统振动能量的时间历程、FFT和相应振动能量轨道变化,如图20所示。
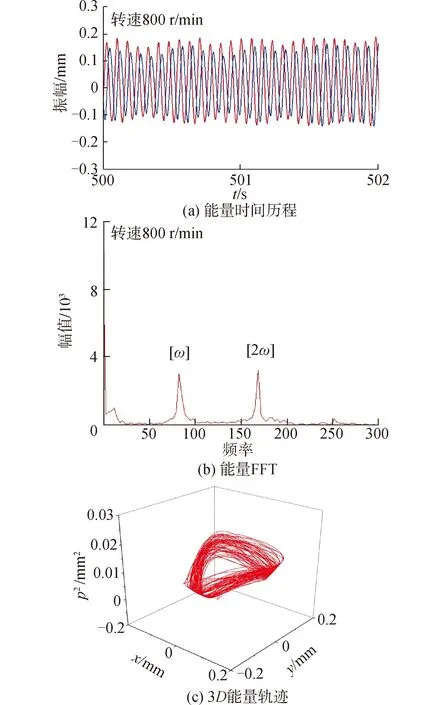
图20 实验结果(主谐波共振)Fig.20 Experimental results(the major critical speed)
图20(a)表示此刻振动能量周期变化的时间历程。图20(b)显示此时振动能量FFT中明显观察到2ω和ω成分。图20(c)显示3D振动能量轨迹呈对折形状的闭合曲面。
4 结论
1)能量空间分析方法可实现系统振动特性分析。裂纹转子在高转速时,在振动能量空间分析中超谐波2ω成分保存更加明显,特别有利于在高转速条件下对裂纹进行检测。
2)在各谐波共振附近,能量轨道呈对折曲面。在主谐波共振和1/2次亚谐波共振附近,呈倾斜曲面,其X-Y平面上投影中随裂纹加深而呈现出“凹”和“凸”字形,且裂纹变化会引起振动能量轨道的旋转,即利用能量轨道变化可以对裂纹转子的参数变化进行定性分析。
3)实验验证了振动能量空间分析方法的正确。
