团簇Mo3S4异构转化热力学与动力学研究

朱依文，方志刚，毛智龙，刘立娥，宋静丽

(辽宁科技大学 化学工程学院，辽宁 鞍山 114051)

随着能源使用量的不断攀升，化石燃料在使用过程中产生的各种气体会使全球气候发生变化，同时火电站发电所剩“余热”被排入河流、海洋中，对生态环境造成严重的污染。为了改善这一问题，氢气作为可持续的能源载体和燃料来源以及未来能量转换的核心，受到国内外学者的高度关注。目前制取氢气的常用方法为电解水析氢，然而在寻找积极、稳定和低成本的催化剂方面仍然存在一些挑战。虽然铂碳(Pt/C)催化剂性质优良，但其高昂的成本和不丰富的产量限制了它的应用。非晶态合金因其优异的稳定性[1]、催化性能[2]、电化学性能[3]、磁学性能[4-5]而备受瞩目，因此采用非晶态过渡金属催化剂是实现催化氢转化的最有效的方法。其中过渡金属硫化物既可作为铂族金属的低成本替代品应用于化石燃料氢脱硫(HDS)工业中，又可应用于不饱和基材的氢化，能够有效地进行催化氢反应[6-8]。Mo-S体系非晶态合金作为一种新型催化剂材料，不仅在生物医学和工业催化方面具有潜在应用[9-11]，而且能够对最重要的电化学过程之一氢进化反应(HER)进行高效电解[12]。同时，Mo-S体系非晶态合金催化剂被发现在碳基电极表面的电化学HER中显示出非常高的分子催化效率。迄今为止的Mo-S体系二元团簇的研发工作已在实际操作环境中得到广泛应用[13]。Jaramillo等人[14]对两种高比表面积气体进行了膜电极组件评价和高定向热解石墨(HOPG)上的扩散电极计算，并使用隧道显微镜(STM)对团簇的亚单分子膜进行扫描，对每个集群的活动进行量化并与其它催化剂进行了活性比较，发现团簇Mo3S4可作为一种高效的电催化剂应用于电化学领域。因此从理论和实验方面进一步探讨团簇Mo3S4的性质是十分有必要的，但目前大多数已有的研究都是从宏观实验角度出发，而对其理论方法的研究相对较少。本文以团簇Mo3S4作为局域模型出发，对其异构化反应机制进行分析研究，以期为今后有关该体系的理论指导及实际应用提供理论依据。

1 模型与计算方法

1.1 模型设计

依据拓扑学原理[15]对团簇Mo3S4的初始构型进行空间结构的设计，以五棱双锥型、戴帽四棱双锥型和戴帽三角双锥型为基础，通过变换不同原子的位置，尽可能多的设计出团簇Mo3S4的构型方案。

1.2 理论计算方法

采用密度泛函理论[16-17]可以对开壳层和过渡金属进行准确计算，利用Gaussian09程序对其单、三重态下的初始构型进行计算，在B3LYP/Lan12dz水平下进行优化，对各构型中Mo、S原子采用Hay等人[18]的含相对论校正的有效核电势价电子从头计算基组，即18-eECP 双ξ基组(3s,3p,3d/2s,2p,2d)，并对S原子加上极化函数ξS,d=0.55[19]。运用QST2方法得到各优化构型之间异构化反应的过渡态空间结构。

2 结果与讨论

2.1 团簇Mo3S4的优化构型及过渡态构型

经由上述方法计算，在排除虚频和相同构型后最终获得8种稳定存在的优化构型，进而得到团簇Mo3S4的8种优化构型。为便于观察将能量最低的构型1(1)作为能量基准点，其余构型能量参照构型1(1)按照相对能量从低到高顺序依次列出，如图1所示。其中右上方括号内数字表示自选多重度，实线键上的数字表示键长，单位是nm。

图1 团簇Mo3S4优化构型及能量图

图2为上述各优化构型发生异构化反应时过渡状态(Transition State)的空间结构，可用TS表示，过渡态构型经过IRC方法验证后，符合验证条件。表1列出了团簇Mo3S4过渡态构型的能量和具体的虚频数值。过渡态构型中虚线表示生成键或者断裂键，实线表示未改变键，负值表示其虚频值，箭头的方向表示原子位移的方向，箭头的长度表示原子位移的大小，C1表示其对称性。观察图2发现，过渡态构型主要以单帽四棱双锥型(TS4(3)→1(3)、TS3(3)→2(3)、TS3(1)→3(3)、TS3(1)→2(1)、TS2(1)→4(3))、双帽三角双锥型(TS3(1)→4(3)、TS4(1)→3(3))、五棱双锥型(TS4(1)→1(1))为主。

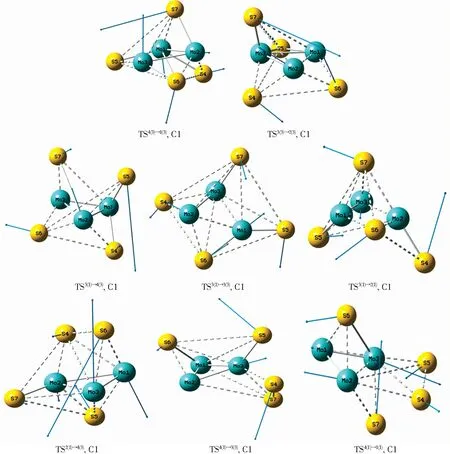
图2 团簇Mo3S4异构化转化后过渡态构型图

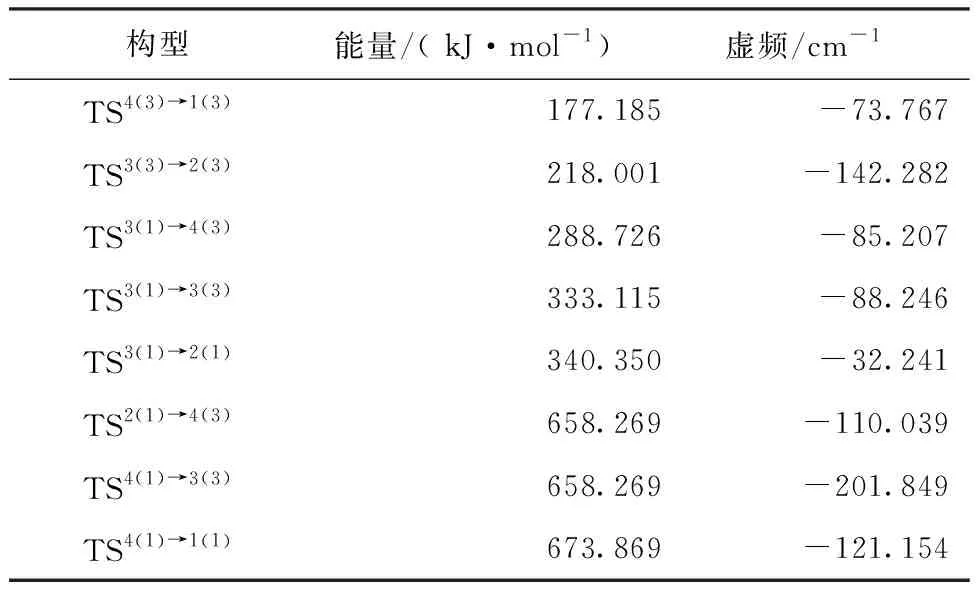
表1 团簇Mo3S4过渡态构型的能量和虚频

2.2 团簇Mo3S4异构转化的热力学研究

2.2.1 团簇Mo3S4的热力学参数

在化学热力学中，物质的热力学能(U)、吉布斯自由能(G)、焓(H)、熵(S)作为热力学参数，对分析物质的状态及发生化学反应起到重要作用，因此为深入研究团簇Mo3S4发生异构化反应进行转化的情况，将所有上述基本参数的数据列于表2中。由化学热力学中对G、H、S的定义式可得:G=H-TS，U=H-PV，所以H-U=PV，U-G=TS-PV。同时由表2可得H-U和U-G均为正值，说明构型的体积值对其能量的影响比其熵值对能量的影响更小。

根据表2中的数据，以不同构型作为研究对象，可以发现：所有构型的能量(U)、吉布斯自由能(G)和焓(H)均满足1(1)<1(3)<2(3)<3(3)<4(3)<2(1)<3(1)<4(1)；观察表中的熵值数据可知，构型1(1)的熵最小，说明该构型的系统有序性最高。

表2 团簇Mo3S4优化构型热力学参数

2.2.2 团簇Mo3S4异构化反应的限度和方向

在压强为1.0×105Pa、温度为298.15 K的条件下对各优化构型进行异构化反应的理论计算，由范特霍夫方程lnK0=-ΔH/RT+ΔS/R，结合表2的数据，可计算出异构化反应的平衡常数K0，进而对反应限度进行讨论，数据与结果见表3。

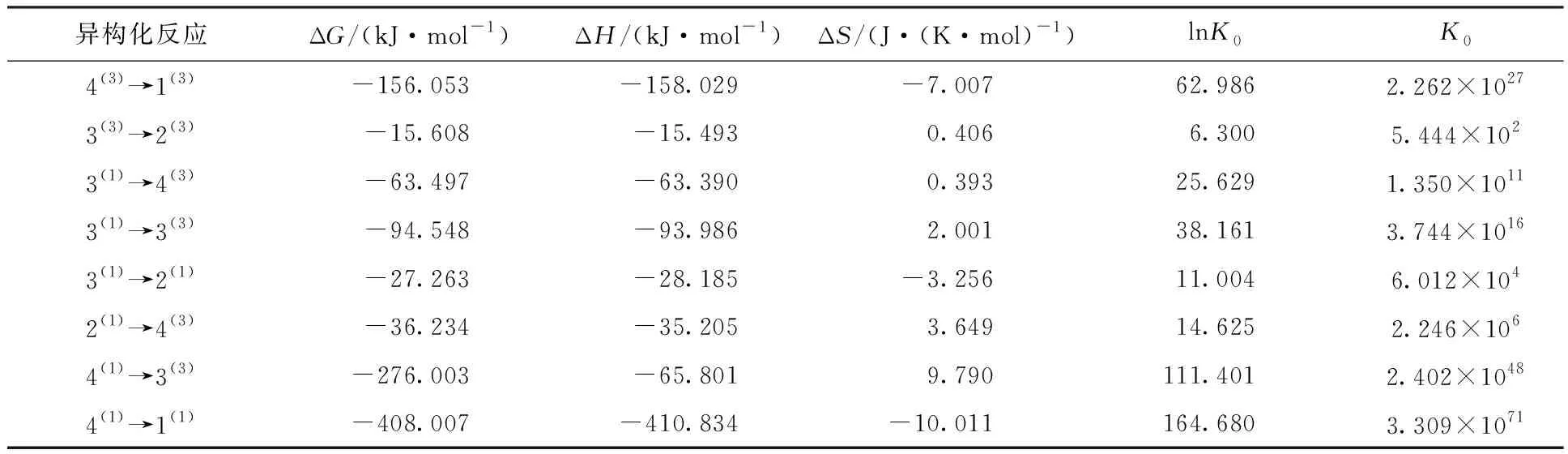
表3 团簇Mo3S4异构化反应的平衡常数

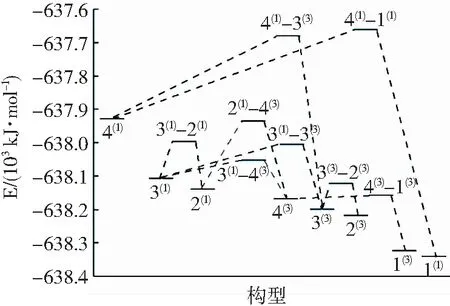
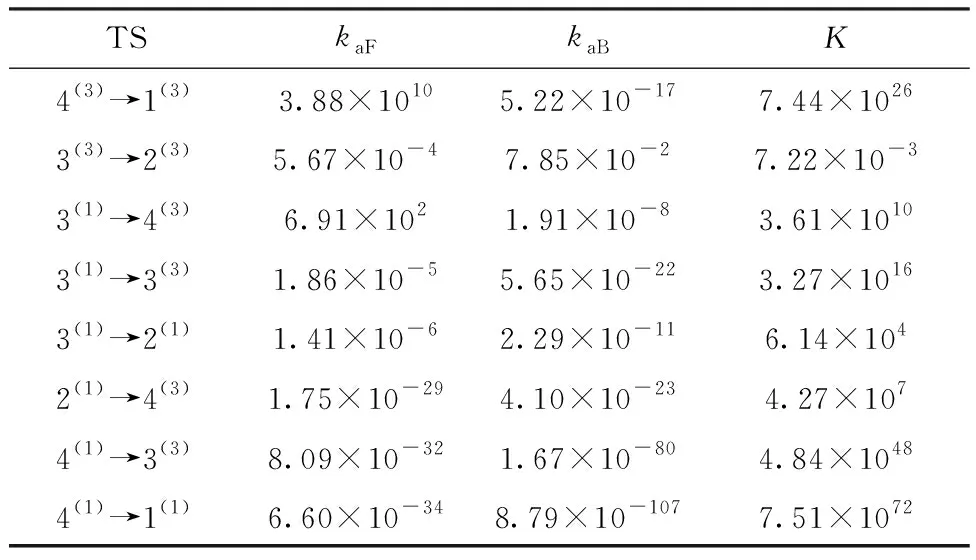
平衡常数K0是平衡进行程度的标志，可以根据其数值大小判断化学反应进行的程度。K0值越大，说明该反应正向进行程度越大，平衡体系中生成物所占的比例越大；反之，则说明反应进行越不完全。对于一般反应而言，K0>105时，该反应正向进行的限度远大于逆向进行的限度；10-5

分析表3中的数据可知，在已有的异构化反应中，只有反应3(3)→2(3)和3(1)→2(1)的平衡常数小于105，而其他反应均大于105，说明反应3(3)→2(3)和3(1)→2(1)的反应程度不太彻底，而其余异构化反应的正反应的限度远大于逆反应的限度，反应程度较为彻底。

在一个反应中，吉布斯自由能变(ΔG)、焓变(ΔH)和熵变(ΔS)对于一个反应能否自发进行和方向有着至关重要的影响，当ΔG<0时，理论上可将该反应视为自发进行，ΔH<0表示为放热反应。因此由表3中的相关数据不难发现，所有异构化反应在理论上均能自发进行。同时，由吉布斯-亥姆霍兹方程(Gibbs-Helmholtz equation)ΔG=ΔH-TΔS可得，在异构化反应中由于反应4(3)→1(3)、3(1)→2(1)及4(1)→1(1)的熵变小于0并且焓变小于0，所以为了使反应的吉布斯自由能变小于0，需要较低的温度来抵消熵变小于0的影响，进而说明这3个异构转化反应在低温下易于自发进行。

2.3 团簇Mo3S4异构转化的动力学研究

2.3.1 团簇Mo3S4异构转化过程的活化能

过渡态理论认为反应物转化为产物的过程需要经过一个高能量的活化状态(过渡态)，此过程需要吸收的能量被称为活化能Ea。过渡态能够提供反应动力学信息，对于过渡态的研究能够进一步探索其反应机理。

表4列出了团簇Mo3S4的8个异构转化过程中各物种二次收敛自洽场(SCF)流程的方法，近似求出其总能量，表中EaF表示异构化反应正向进行时的活化能，EaB表示异构化反应逆向进行时的活化能。为了更直观展现构型异构转化反应过程中能量的变化，依据表4中的相关数据绘制图3。在指定温度下，反应的活化能越低，活化分子数越多则反应速率越快，说明该反应越容易进行；反之，活化能越高，说明越不易进行该反应。由表4中可知，所有异构转化反应的EaF均小于EaB，说明在所有异构化反应中正向反应比逆向反应更容易进行，即能量高的构型更容易转化为能量低的构型。

根据单分子反应完成97%时反应时间

t=-(ln0.03)/k

(1)

其中k=2.1×1010×T×e-1000ΔE/(1.9859×T)，ΔE表示活化能。由公式(1)计算可得，在常温常压下，当单分子过渡态反应的活化能约为88 kJ/mol时反应需要进行22.3 min，而当活化能约为92 kJ/mol时则需要2 h。因此，当单分子异构化反应的活化能小于88 kJ/mol时可以在常温下进行，而大于88 kJ/mol时，则在常温下较难进行。

据此结合上述反应限度的分析对相关异构化反应进行讨论：反应4(3)→1(3)的正反应活化能最低(EaF=9.563 6 kJ/mol,远小于88 kJ/mol)，逆反应活化能较高(EaB=167.125 5 kJ/mol,大于88 kJ/mol)，且反应限度较大(平衡常数K0=2.262×1027>105)，说明在常温下构型4(3)会通过正反应4(3)→1(3)彻底转化为构型1(3)，即构型1(3)在该反应中能够稳定存在。对于3(3)→2(3)而言，正反应活化能为81.543 3 kJ/mol,小于88 kJ/mol，逆反应的活化能为96.605 3 kJ/mol,大于88 kJ/mol，反应限度较小(平衡常数K0=5.444×102<105)说明在常温下反应3(3)→2(3)能够发生，构型3(3)通过正反应3(3)→2(3)较为彻底的转化为构型2(3)，即构型2(3)在该反应中能够稳定存在。同理，反应3(1)→4(3)的正反应活化能58.043 5 kJ/mol,小于88 kJ/mol，逆反应活化能121.104 9 kJ/mol,大于88 kJ/mol，反应限度较大(平衡常数K0=1.350×1011>105)，说明构型3(1)能通过正反应3(1)→4(3)彻底转化为能够稳定存在的构型4(3)。而反应3(1)→3(3)、3(1)→2(1)、2(1)→4(3)、4(1)→3(3)、4(1)→1(1)的正、逆反应活化能均大于88 kJ/mol，说明这些反应很难发生，即构型3(1)、2(1)、4(1)能够稳定存在。但通过上述分析可知由于发生反应3(1)→4(3)，构型3(1)易进行正向异构化反应进而转化为构型4(3)，综上所述，构型1(3)、2(3)、2(1)、4(1)能够稳定存在。

表4 团簇Mo3S4异构化过程的能量及活化能

观察图3不难发现，在常温常压下以构型3(1)、4(1)为反应物可以通过5条不同途径的异构反应最终转化为构型1(3)、2(3)、1(1)，途径如下:Ⅰ3(1)→4(3)→1(3)；Ⅱ3(1)→3(3)→2(3)；Ⅲ 3(1)→2(1)→4(3)→1(3)；Ⅳ4(1)→3(3)→2(3)；Ⅴ4(1)→1(1)。理论上构型3(1)作为3个异构化反应的反应物，更易发生异构化反应进而转化成构型4(3)、3(3)、2(1)。结合表4分析可知途径Ⅰ的所有反应EaF均小于88 kJ/mol，EaB均大于88 kJ/mol；而途径Ⅱ中反应3(1)→3(3)和途径Ⅲ中反应3(1)→2(1)、2(1)→4(3)以及途径Ⅳ中反应4(1)→3(3)和途径Ⅴ中反应4(1)→1(1)的EaF、EaB均大于88 kJ/mol，说明在团簇Mo3S4异构化反应中更易发生如途径Ⅰ所示的连串反应。

图3 团簇Mo3S4异构化反应的能垒图

2.3.2 团簇Mo3S4异构化反应的反应速率及平衡常数

为进一步探究团簇Mo3S4各异构化反应的难易程度，表5列出了正、逆反应速率(kaF、kaB)及过渡态的平衡常数K。根据过渡态理论中实际速率常数k(T)=к(T)kTST(к(T)为魏格纳校正系数，kTST为理论速率常数)以及相关数据可以得出正、逆反应速率常数kaF(正反应)和kaB(逆反应)，进而根据K=kaF/kaB可得出反应的平衡常数。

表5 团簇Mo3S4过渡态的正、逆反应速率与平衡常数

由表5可知，除TS3(3)→2(3)、TS2(1)→4(3)外，其余6种异构化反应的正反应速率均大于逆反应速率，且平衡常数K均大于1(数量级达到104～1072)，说明这6种异构转化过程均趋向于向正反应方向转化。根据2.2.2节中对反应限度的判断定义并结合表5中的数据发现，反应3(3)→2(3)和3(1)→2(1)的K值依然小于105，而其他反应的K值还是大于105，这验证了上述结论：反应3(3)→2(3)和3(1)→2(1)进行不太彻底，其余异构化反应较为彻底。

将表5中平衡常数K的数据和表3中的数据相对比，发现不论是从化学热力学的角度，还是从化学动力学的角度，对K值进行计算，二者所得出的值在数量级上基本一致(除反应3(3)→2(3)外，其余反应仅存在0～1个数量级的变化)，说明二者所得到关于反应限度的结论是基本一致的。

3 结 论

本文利用密度泛函理论对团簇Mo3S4异构化反应进行计算，得到新的过渡态构型，分别为：单帽四棱双锥型(TS4(3)→1(3)、TS3(3)→2(3)、TS3(1)→3(3)、TS3(1)→2(1)、TS2(1)→4(3))、双帽三角双锥型(TS3(1)→4(3)、TS4(1)→3(3))、五棱双锥型(TS4(1)→1(1))。根据范特霍夫方程、吉布斯-亥姆霍茨公式、活化能、过渡态理论和阿伦尼乌斯公式，从热力学和动力学这两个角度进行分析，得出以下结论：

1)在异构化反应中，反应3(3)→2(3)和3(1)→2(1)的反应进行程度不太彻底，反应限度较小；反应4(3)→1(3)、3(1)→2(1)及4(1)→1(1)的异构转化反应在低温条件下易于自发进行。

2)在常温下构型4(3)、3(3)、3(1)会通过正向进行的反应4(3)→1(3)、3(3)→2(3)、3(1)→4(3)转化为更稳定的构型1(3)、2(3)、4(3)，即构型1(3)、2(3)能够稳定存在。而反应3(1)→3(3)、3(1)→2(1)、2(1)→4(3)、4(1)→3(3)、4(1)→1(1)很难发生，即构型3(1)、2(1)、4(1)能够稳定存在。但构型3(1)可以发生正向异构化反应转化为构型4(3)，综上所述能够稳定存在的构型为1(3)、2(3)、2(1)和4(1)。

3)除TS3(3)→2(3)、TS2(1)→4(3)外，其余6种异构化反应的正反应速率均大于逆反应速率，且平衡常数K均大于1(可达到104～1072个数量级)，说明这6种异构转化过程均趋向于向正反应方向转化。