有限过载的三维现实真比例导引的捕获区域

张锦林, 李 炯, 雷虎民, 李万礼, 唐 骁

(1. 空军工程大学防空反导学院, 陕西 西安 710051; 2. 空军工程大学研究生院, 陕西 西安 710051)

0 引 言

近年来,各国空天武器快速发展,高空目标的威胁日益剧增,对拦截器性能也提出了更高的要求,为确保成功拦截目标,应使拦截器完成中末交接班,并使得拦截器在中制导结束时,处于有利的拦截状态,即末制导律的捕获区域。

比例导引律(proportional navigation,PN)由于其鲁棒性和工程易实现性,在制导武器领域得到了广泛的应用。PN制导律一般分为两大类。一类是指令加速度方向垂直于拦截器速度方向,主要包括纯PN(pure PN, PPN)及其变式,通常用于大气层内的拦截制导。另一类是指令加速度方向与视线有关的方向,主要包括真PN(true PN, TPN)、现实TPN(realistic PN, RTPN)、广义TPN(generalized TPN, GTPN)、理想PN(ideal PN, IPN)及其变式,更适合于高空拦截场景。其中,TPN和RTPN加速度的方向垂直于视线,大小与视线旋转角速度成正比,能控制视线旋转角速度不发散,使拦截器具有较小的脱靶量,从而实现对目标的直接碰撞。而GTPN和IPN都存在视线方向上的指令加速度,在工程中难以应用,因此TPN和RTPN是更适合高空拦截的制导律。

RTPN是使用实时的视线接近速度来代替TPN中的初始接近速度。文献[19]认为RTPN具有与TPN相似的性能,但具有更大的数学可处理性,因此有许多学者对RTPN进行了研究。文献[20]研究了TPN对非机动目标的相对运动的封闭解,得到了TPN的一个圆形捕获区域。文献[24]推导出二维TPN和RTPN针对非机动目标的捕获区域的形式。文献[19]研究了TPN和RTPN针对二维机动目标的捕获区域,目标的加速度垂直于视线,与垂直视线的相对速度成反比。文献[21]提出了一种新的针对非机动目标和机动目标的RTPN解析解的求解方法。文献[22,25]基于三维非线性耦合相对运动方程集,分析了三维TPN和RTPN对非机动目标和机动目标的性能,但文献[21]、文献[22]和文献[25]机动目标是由TPN、RTPN制导律来引导的。文献[26]得到二维RTPN针对非机动目标和垂直视线方向机动目标的捕获区域,该捕获区域以速度前置角作为约束。文献[29-30]提出了一种相位平面方法来研究三维TPN对非机动目标和机动能力有限的机动目标的捕获区域,但该机动是已知目标准确加速度的情况的机动。

与以前的工作不同,文献[23]、文献[27]、文献[28]和文献[34]利用Lyapunov第二方法分析了制导律的性能针对有上限并垂直于视线的目标加速度,利用Lyapunov第二方法分析了二维RTPN和三维 TPN的性能,但对拦截器的机动大小未限制。文献[28]在文献[27]的基础上加入拦截器机动大小的限制,针对目标垂直视线方向上的机动,得到二维RTPN的捕获区域。文献[34]将该方法应用到现代制导律中,说明该方法应用前景广阔,但针对不机动目标,具有较大的局限性。

结合上述文献可得,目前在高空拦截高速机动目标的捕获区域,还存在以下问题:

(1) 在实际的拦截过程中,目标应该是三维有限机动,且机动幅值会在一定范围内变化,而拦截器的机动过载同样有限,目前针对该条件下捕获区域的研究仍为空白。

(2) 哪些影响因素决定着能否成功捕获目标,各因素的变化对于捕获区域的影响又是怎样的?

基于以上问题,本文针对三维有限机动的高速目标,即加速度方向任意,但大小有限的高速目标,对采用动能碰撞的有限过载的三维RTPN制导律的捕获区域进行分析。首先,介绍了视线旋转坐标系、三维RTPN及其对应的相对运动学关系和假设条件;其次,对捕获进行了定义,采用Lyapunov第二方法证明了视线旋转角速度的渐近稳定性,并得到了有限过载的RTPN拦截任意三维机动目标的捕获区域;然后,对本文捕获区域进行仿真验证以及影响因素分析;最后,给出总结以及本文结论的意义。

1 预备知识

1.1 视线旋转坐标系

图1中,表示以为原点,以、、为轴的惯性坐标系;视线旋转坐标系(line-of-sight rotation coordinate system, LRC)表示以拦截器的质心为原点,以、、为轴的视线旋转坐标系;表示视线方向上的单位矢量,表示沿视线角速度方向上的单位矢量,=×表示视线单位法向量;视线角(line-of-sight,LOS)表示视线,表示拦截器在惯性坐标系中的位置矢量,表示目标在惯性坐标系中的位置矢量,表示拦截器速度,表示目标速度。

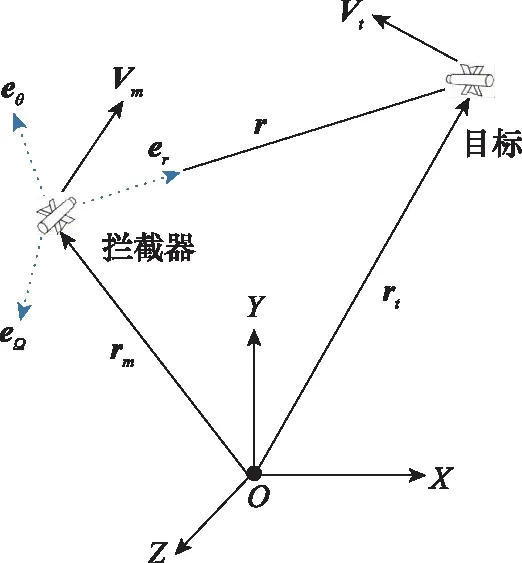
图1 LRCFig.1 LRC

在LRC中建立运动学方程组可以简化三维相对运动学描述的复杂性。LRC中的相对运动可分为两个解耦子运动:

(1) 拦截器与目标在相对位置矢量和速度矢量所跨越的瞬时密切面内的相对运动,称为视线瞬时旋转平面。

(2) 视线瞬时旋转平面的旋转。

以拦截器的质心为原点,三轴(,,)组成的视线旋转坐标系满足关系:

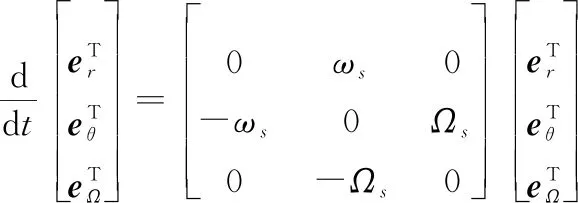
(1)

式中:=表示视线的角速度;=表示视线旋转平面的旋转角速度。

1.2 基本假设条件

为了研究高空中有限过载拦截器拦截任意三维机动目标的捕获问题,首先根据实际拦截情形,确定拦截器与目标加速度的方向与大小。拦截器加速度大小受饱和过载约束,方向有导引方法确定;目标的加速度大小受空气密度制约,方向任意。其次,三维拦截的几何形状如图1所示。为简化三维RTPN的性能分析,假设如下。

将拦截器和目标视为质点,并忽略重力以及空气阻力对拦截器和目标的影响。

当拦截器与目标之间的距离小于导引头的最大作用距离时,则认为拦截器成功跟踪目标,能够获取目标信息。

不考虑制导和控制误差。

在高空拦截高速目标,采用动能碰撞拦截。

1.3 拦截器与目标相对运动分析

结合图1和基本假设条件,拦截器与目标相对位置矢量为

=-=r

(2)

式中:=/r是视线方向的单位矢量。

对式(2)进行求导可得,拦截过程中两者之间的相对运动关系为

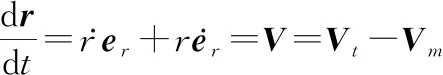
(3)

将式(1)代入式(3)得

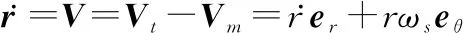
(4)

对式(4)进行求导,可得

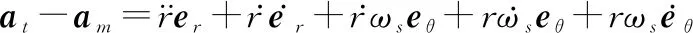
(5)

将式(1)代入式(5)得

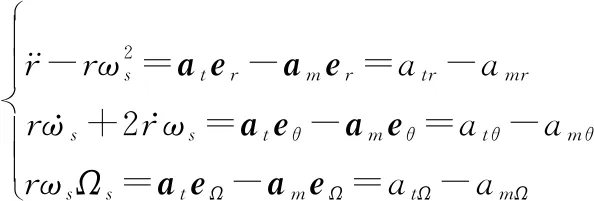
(6)

式中:、 、分别表示目标加速度分解到视线旋转坐标系的各坐标轴、、上的分量大小;、 、分别表示拦截器加速度分解到视线旋转坐标系坐标轴、、上的分量大小。

三维RTPN制导的指令加速度表达式:

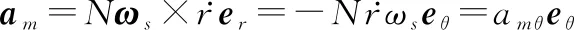
(7)

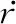
将式(7)代入式(6)得

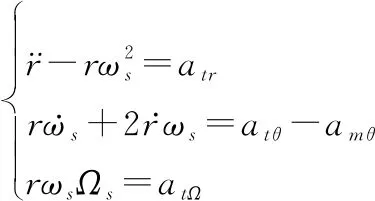
(8)

且由式(4)可得

=-=

(9)

分析式(9)得,目标与拦截器在垂直视线瞬时旋转平面上,速度投影差值为零,如果目标存在垂直视线瞬时旋转平面的加速度,那么视线瞬时旋转平面将发生旋转,以满足式(9)所示条件。这也是采用视线旋转坐标系的优点,能够将三维拦截问题转化为视线瞬时旋转平面内的拦截问题。

假设目标的加速度满足:

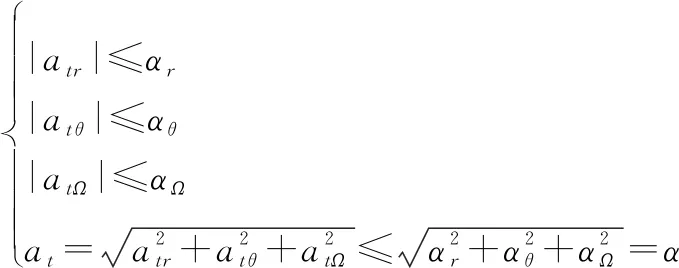
(10)

式中:、、、是常数。在实际的拦截作战中,目标的加速度上限可以根据实际目标情报以及当前科技发展水平确定。

2 现实真比例导引律性能分析

使用三维RTPN制导进行高空拦截时,最重要的是能否对目标进行捕获,首先确定高空碰撞杀伤捕获的定义。然后对视线旋转角速度进行Lyapunov稳定性分析,最后得到有限过载三维RTPN的捕获能力。

2.1 捕获目标的定义

对目标的捕获的定义。

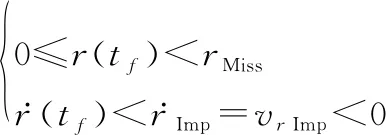
(11)

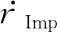
而一般的捕获定义为

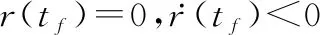
(12)

将根据高空拦截的实际特点,即动能拦截,分析式(11)和式(12)可知,式(11)的表达更加符合实际拦截目标捕获的定义。

2.2 稳定性分析

在分析三维RTPN性能之前,首先对拦截器视线角速度进行Lyapunov稳定性判定,得到拦截器视线角速度渐近稳定的,并且其变化边界与初始视线角速度、目标加速度、容许碰撞速度以及导航比有关。

由式(8)可得,采用三维RTPN制导的拦截器能够对满足式(10)的任意三维机动目标进行拦截,如果导航比满足:

>2

(13)

并且视线接近速度满足:

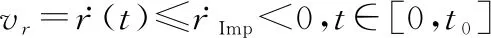
(14)

式中:∈(0,+∞)为常数。则

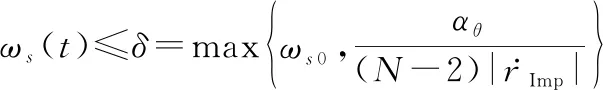
(15)

一定成立。

首先用反证法对式(15)的不等式进行证明。如果式(15)不成立,从()的连续来看,必然存在一些常数,∈[0,]使得

()=

(16)

()>,<≤

(17)

选取如下Lyapunov函数:

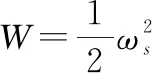
(18)

对式(18)求时间的一阶导数并结合式(8)的第二式可得

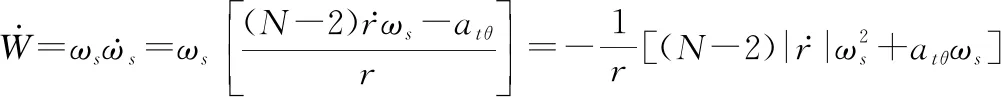
(19)

将式(10)和式(14)代入式(19)中可得

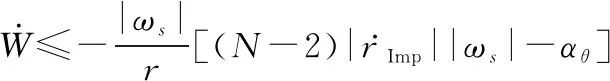
(20)

当∈(,]时,的边界值已经在式(15)假设出,将式(17)代入式(20)中可以得到:

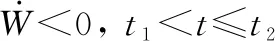
(21)

根据式(21)可得,在拦截过程中是符合Lyapunov稳定的,即

()≤,<≤

(22)

式(22)的结果与式(17)相矛盾,因此式(15)得以证明。

证毕

2.3 捕获区域的确定

捕获区域可认为是一个状态空间,与拦截器和目标相对运动状态有关,当拦截器与目标的相对运动状态进入该状态空间时,式(11)成立,即拦截器最终能成功捕获目标。

当拦截器与目标之间符合式(8)中的制导关系,且目标加速度满足式(10)时,那么视线接近速度在制导过程中就有了一定的约束,其视线接近速度满足:

(23)

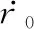
由式(8)第一式和式(10)可得

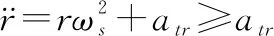
(24)

对等式两边进行积分可得

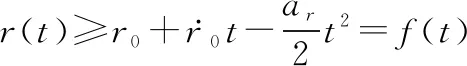
(25)

在实际的拦截过程中应满足()≥0,为了保证()≥0,应使()≥0,而当()=0时,满足下列关系式:

(26)

由式(26)的第二式可证明式(23)成立。

证毕

确定导航比的取值范围,如果拦截器饱和机动加速度为 max,由式(8)可得,采用有限过载的三维真比例导引的拦截器能够对满足式(10)的任意三维机动目标进行拦截,如果拦截器与目标状态满足式(14)。

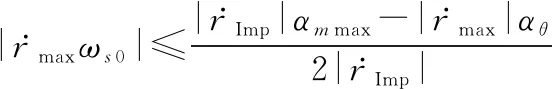
(27)

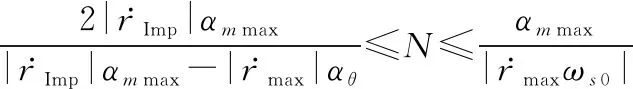
(28)

则

| |≤ max

(29)

成立。

由式(27)可得

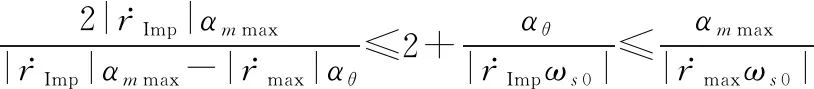
(30)

由于式(30)的推导结果不易直接得到,下面对关键步骤进行说明。

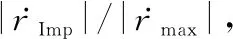
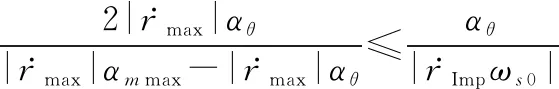
(31)

对式(31)的两边同时加2,化简可得式(30)左边的不等式。

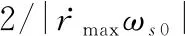
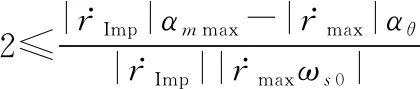
(32)

对式(32)化简得式(30)右边的不等式。

由式(30)可确定导航比的取值范围:

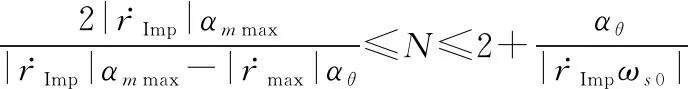
(33)

或者

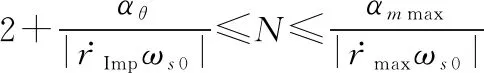
(34)

因为式(33)和式(34)合并即为式(28),两式又分别代表的两种约束条件,且的取值均满足定理1中的条件,所以可以利用定理1针对的两种约束条件,对拦截器的饱和机动加速度 max进行分析。

由式(33)右边不等式可得

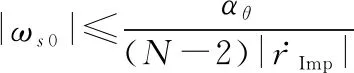
(35)

通过式(7)和式(15)可得

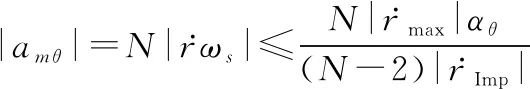
(36)

同时由式(33)左边的不等式可得

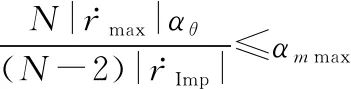
(37)

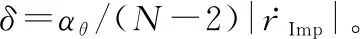
由式(34)左边不等式可得

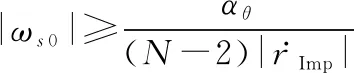
(38)

通过式(7)和式(15)可得

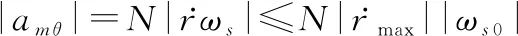
(39)

同时由式(34)右边的不等式可得

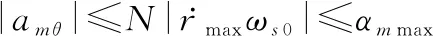
(40)

最后通过式(39)和式(40)可以证明式(29)成立,此时=| 0|。

证毕

说明采用三维RTPN制导且导航比在一定区间内时,拦截器与目标初始运动状态满足一定条件后,拦截器的加速度在拦截作战过程中能始终满足小于拦截器的饱和机动加速度 max。

由式(8)可得,采用有限过载的三维RTPN制导的拦截器能够对满足式(10)的任意三维机动目标进行拦截时,制导的过程中应满足:

()>

(41)

如果拦截器与目标之间的初始相对运动状态满足:

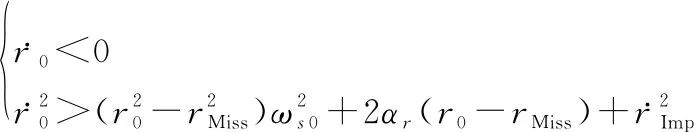
(42)

同时其导航比满足:

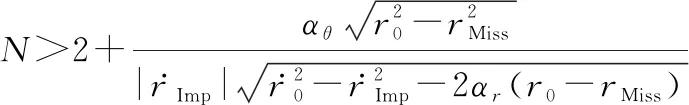
(43)

那么

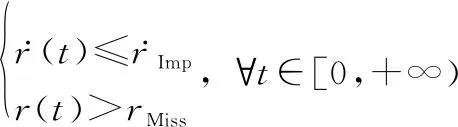
(44)

一定成立。

不等式(44)意味着一定存在一个时间常数∈(0,+∞)使式(11)有效,从而保证对目标的捕获。

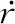
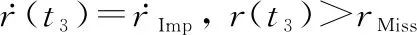
(45)

成立。同时存在:

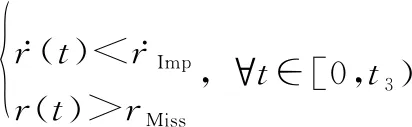
(46)

即在视线距离到达容许脱靶量之前,视线接近速度先到达容许碰撞速度。

由式(8)的第一式可得

(47)

对式(47)进行积分可得在∈[0,)时:

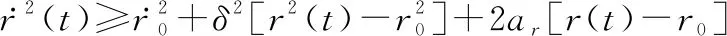
(48)

令

即在=时

(49)

成立。

由式(46)可得,()>,代入式(49)可得

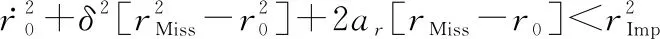
(50)

下面根据式(15),分两种条件对式(50)进行讨论,条件如下:

条件1:

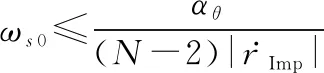
(51)

条件2:

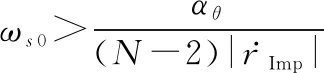
(52)

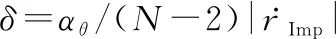
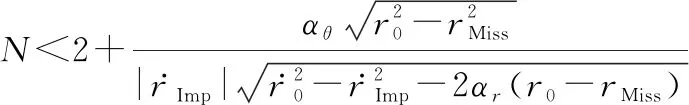
(53)

式(51)与式(43)矛盾,证明式(44)成立。

此时由式(43)和式(51)可得到式(42)。

条件2成立时,= 0成立,由(50)可得

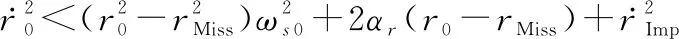
(54)

式(54)与式(42)矛盾,证明式(44)成立。

此时,由式(42)和式(52)可得到式(43)。

证毕

从该定理4可知,当对拦截器的过载即加速度没有限制时,定理4为采用RTPN制导的拦截器追击任意三维机动目标提供了一个充分但非必要的捕获条件,也对导航比取值进行了一定的约束。与此同时,定理1和定理4也说明了目标各方向上加速度上限对于捕获区域的影响,决定捕获区域的面积,值越大相应的捕获区域面积越小,和共同决定了三维RTPN制导的指令加速度的上界,不影响目标的捕获。

为方便描述,对捕获区域进行总结,由式(23)和式(27)可得

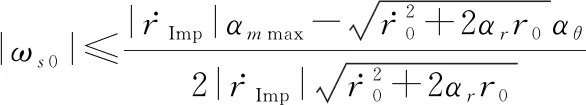
(55)

由式(42)可得

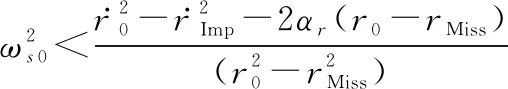
(56)

为了更加清晰地描述拦截器与目标初始运动状态与捕获区域之间的关系,引入初始航向误差,表达式如下:

0= 0

(57)

式中: 0位于视线瞬时旋转平面内,表示拦截器与目标的初始航向误差。该速度是相对速度,方向垂直于视线方向,另一种表达形式为

0=0-0

(58)

将式(11)、式(14)和式(57)代入式(55)和式(56)得

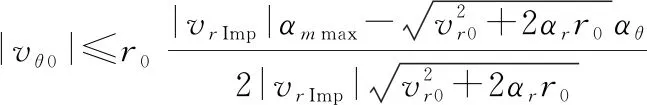
(59)

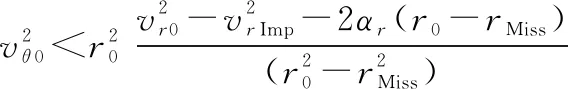
(60)

由式(59)和式(60)中可得,对拦截器的过载有限制时,该捕获区域和下列参数有关:拦截器捕获目标初始距离、初始视线接近速度、初始航向误差以及容许碰撞速度和容许脱靶量;拦截器饱和机动加速度;目标加速度在、方向上的上限。

因为拦截任意三维机动目标的捕获区域问题是非线性问题,无法求取其充分必要条件,所以本文求取的捕获区域为拦截器成功捕获目标的充分不必要条件,即满足式(59)和式(60)捕获条件一定能够成功拦截目标,但并不意味着不满足捕获条件一定不能捕获目标。

3 捕获区域仿真分析

本节将对捕获区域进行分析和验证,由两个小节组成。第31节针对高速目标在捕获区域内外分别对目标的拦截场景和低速目标在捕获区域内的仿真,以验证本文所证捕获区域的有效性。第32节中分析捕获区域的影响因素对于捕获区域面积的影响。

3.1 捕获区域有效性验证

在表1条件下,高速目标采用极限加速度进行机动的捕获区域如图2所示。仿真情形1与仿真情形2分别是在如图2所示的捕获区域上边界内外,来对捕获区域的有效性进行验证。仿真情形3是针对低速目标进行的捕获区域验证。3种仿真情形中拦截器的初始速度状态相同。

表1 捕获区域的6个影响因素

图2 表1数据下的捕获区域Fig.2 Capture area under the data in Table 1

由式(59)和式(60)可知,在拦截器最初捕获目标时,其捕获区域已经由表1中6个影响因素确定,针对某高速目标 6个影响因素数据如表1所示,其中重力加速度取9.8 m/s。

根据表1中的数据结合式(59)和式(60),得捕获区域如图2所示。

在图2的捕获区域内,当初始视线接近速度小于容许碰撞速度时,目标与拦截器初始视线接近速度越小,两者在视线瞬时旋转平面内的初始航向误差范围越大。

3.1.1 仿真情形1

拦截器与目标的初始状态在本文捕获区域内时,当目标采用表1中的极限加速度进行机动时,拦截器初始位置(0 km,18 km,0 km),目标位置(69.9 km,33 km,69.9 km),拦截器与目标在速度视线旋转坐标系中的速度分别为(1 500 m/s,200 m/s,-500 m/s),(-4 400 m/s,440 m/s,-500 m/s),其对应在固定坐标系中速度约为(716.3 m/s,27.3 m/s,1 423.4 m/s),(-3 383.5 m/s,-1 090.1 m/s,-2 676.4 m/s),此时初始拦截器与目标初始相对速度为(0, 0,0)=(-5 900,235,0)m/s,并设定目标在上的过载为1。

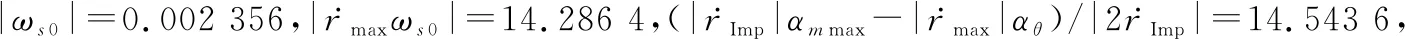
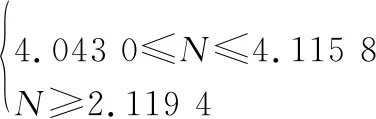
即导航比取值范围为4043 0≤≤4115 8。

导航比分别取27、41、55时的仿真结果分别如表2、图3和图4所示。

表2 情形1下的终端脱靶量

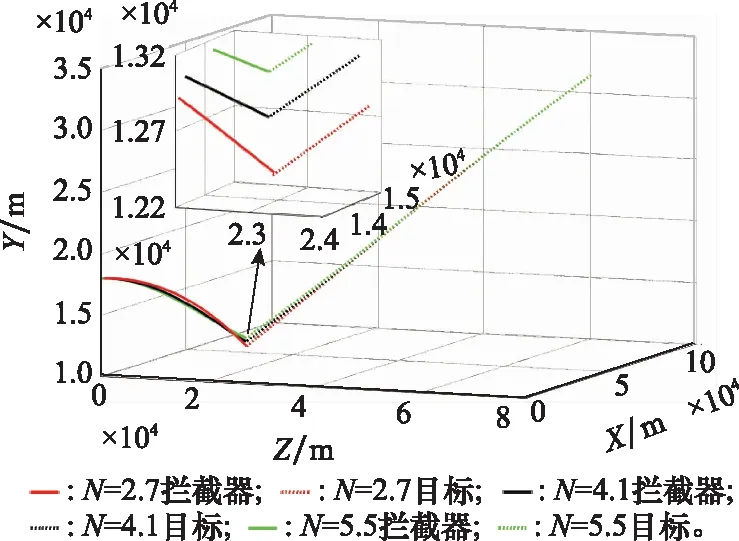
图3 情形1下的拦截轨迹Fig.3 Interception trajectory in case one

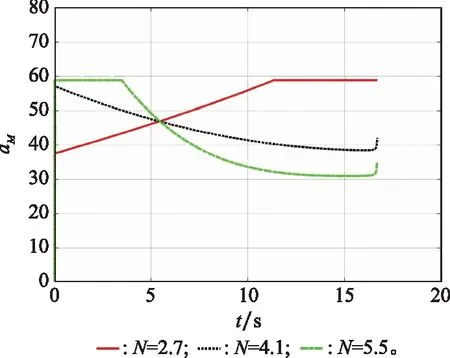
图4 情形1下的拦截器加速度Fig.4 Interceptor acceleration in case one

从表2和图3中能直接观察到,取27时,拦截器未成功捕获目标,原因是拦截器在拦截后期过载受限,未能成功拦截;取4.1、5.5时,拦截器成功捕获目标,虽然后者在拦截前期过载达到饱和,但后期仍处于饱和过载以内,仍能够成功捕获目标。

图3、图4是在仿真情形1条件下,导航比分别取2.7、4.1、5.5时,拦截器拦截目标的轨迹图和加速度图,目标是在视线旋转坐标系上采用极限加速度来验证捕获区域的有效性,而在拦截过程中,不同的导航比将导致拦截器不同的过载以及拦截轨迹,这就进一步导致拦截过程中视线旋转坐标系的差异,进而导致了目标的运动轨迹存在一定的差异,是合理的。

图5展现了在仿真情形1时,拦截器与目标的相对速度在捕获区域内的变化曲线,拦截器成功捕获目标时,拦截器与目标接近或处于零控拦截流形状态(即位于图2中=0的横轴上),这与文献[3,19]中成功捕获条件相符合;拦截器在取27时,未能捕获目标,在拦截后期远离零控拦截流形状态,原因是持续机动的目标与拦截器接近,视线距离开始减小,而目标与拦截器在此时仍未处于零控拦截流形状态。从式(8)的第3式可得,视线瞬时旋转平面的旋转角速度开始增大,导致视线轴剧烈旋转,目标与拦截器相对速度也变化剧烈,导致拦截器持续远离零控拦截流形状态。

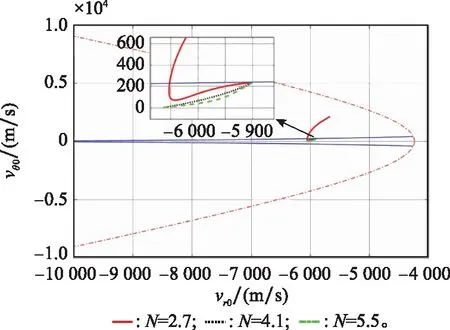
图5 情形1下捕获区域曲线Fig.5 Capture area curve in case one

在仿真情形1下,成功的验证了在捕获区域内,拦截器能对目标进行捕获。

312 仿真情形2

拦截器与目标的初始状态不在本文捕获区域内时,当目标采用表1中的极限加速度进行机动时,拦截器初始位置(0 km,18 km,0 km),目标位置(69.9 km,18 km,69.9 km),拦截器与目标速度在视线旋转坐标系中的速度分别为(1 500 m/s,200 m/s,-500 m/s),(-4 400 m/s,550 m/s,-500 m/s),其对应在固定坐标系中速度约为(716.3 m/s,27.3 m/s,1 423.4 m/s),(-3 371.3 m/s,-1 203.8 m/s,-2 664.2 m/s),此时两者的相对速度为(0, 0,0)=(-5 900,350,0)m/s,并设定目标在上的过载为1。

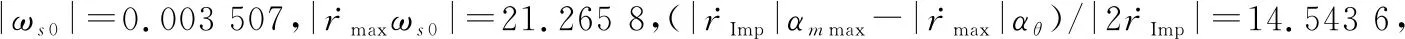
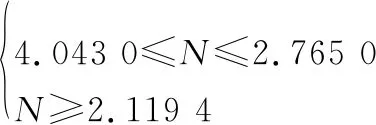
即对应拦截器加速度始终小于饱和加速度时,导航比为空集,这与拦截器与目标的初始状态不在本文捕获区域内假设相符合。

为了验证本文捕获区域的正确性,导航比的取值与仿真情形一相同,分别取27、41、55进行仿真。

表3是在仿真情形2下,目标与拦截器的终端脱靶量。从表3、图6和图7中能直接观察到,导航比分别取27、41、55时,拦截器均未成功捕获目标,原因是拦截器与目标的初始航向误差 0过大,导致拦截器在拦截过程中对过载的需求超过了拦截器的饱和机动过载,最终导致捕获失败。

表3 情形2下的终端脱靶量

图6～图8是在仿真情形2条件下,导航比分别取2.7、4.1、5.5时,拦截器拦截目标的轨迹图、加速度图和相对速度在捕获区域内的变化曲线图。从图7可得,当目标取视线旋转坐标系下的极限加速度,导航比取4.1和5.5时,两者拦截器的加速度都始终处于饱和机动加速度状态,这也导致两种导航比下,拦截器的运动轨迹和运动状态完全相同,这也解释了在图6和图8中,两者的图像完全重合问题。

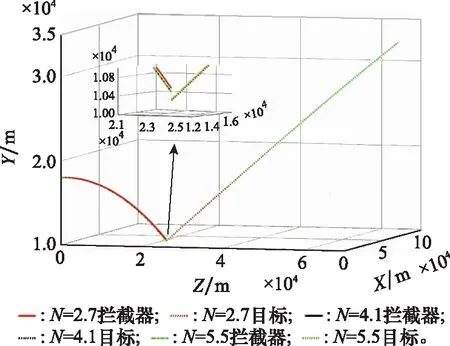
图6 情形2下的拦截轨迹Fig.6 Interception trajectory in case two

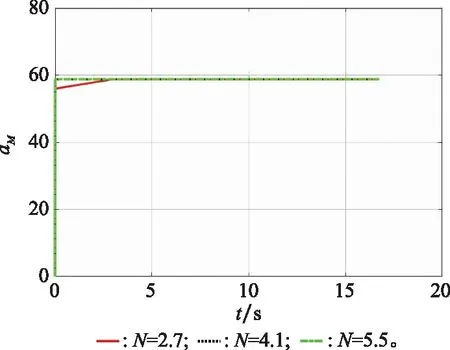
图7 情形2下的拦截器加速度Fig.7 Interceptor acceleration in case two

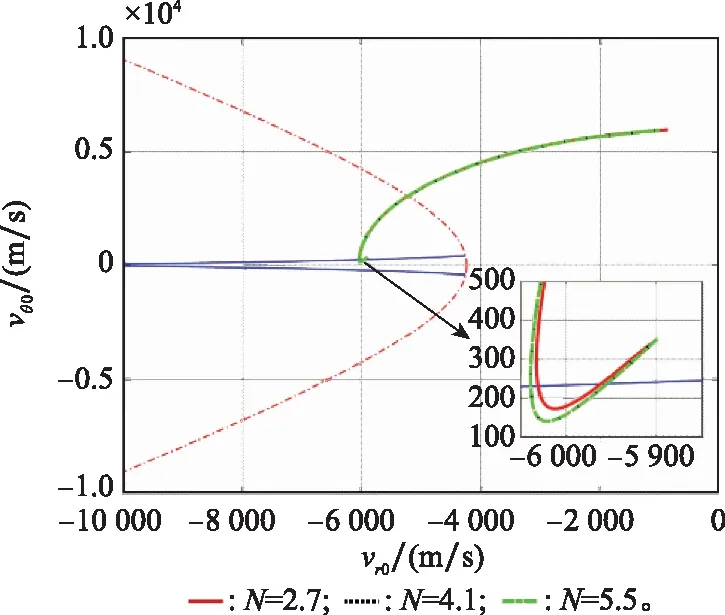
图8 情形2下捕获区域曲线Fig.8 Captures area curve in case two

在图8中,拦截器与目标初始状态在捕获区域外,最终都未能够进入零控拦截流形状态,捕获失败,原因与仿真情形1中导航比为2.7时相同。

在仿真情形2下,成功的验证了在捕获区域外,拦截器不能对目标进行捕获。

3.1.3 仿真情形3

针对低速目标特性,在表1的基础上,修改捕获区域的两个影响因素的参数如表4。在表4条件下,低速目标采用极限加速度进行机动的捕获区域如图11所示。仿真情形3是在如图11所示的捕获区域上边界内,来对捕获区域的有效性进行验证。

表4 修改捕获区域的影响因素

拦截器与目标的初始状态在本文捕获区域内时,当目标采用表1中的极限加速度进行机动时,拦截器初始位置(0 km,0 km,0 km),目标位置(0 km,0 km,30 km),拦截器与目标在速度视线旋转坐标系中的速度分别为(1 423.4 m/s,710.4 m/s,95.8 m/s),(-500 m/s,920 m/s,95.8 m/s),其对应在固定坐标系中速度约为(716.3 m/s,27.3 m/s,1 423.4 m/s),(924.9 m/s,7.2 m/s,-500.0 m/s),此时初始拦截器与目标初始相对速度为(0, 0,0)=(-1 923.4,209.6,0)m/s,并设定目标在上的过载为1。

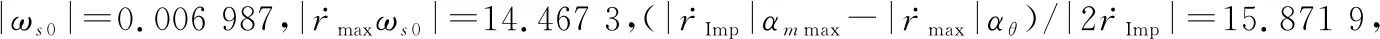
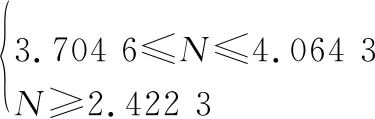
即导航比取值范围为3704 6≤≤4064 3。

导航比分别取27、39、51时的仿真结果分别如表5、图9～图11所示。表5是在各上述导航比下,目标与拦截器的终端脱靶量。

表5 情形3下的终端脱靶量

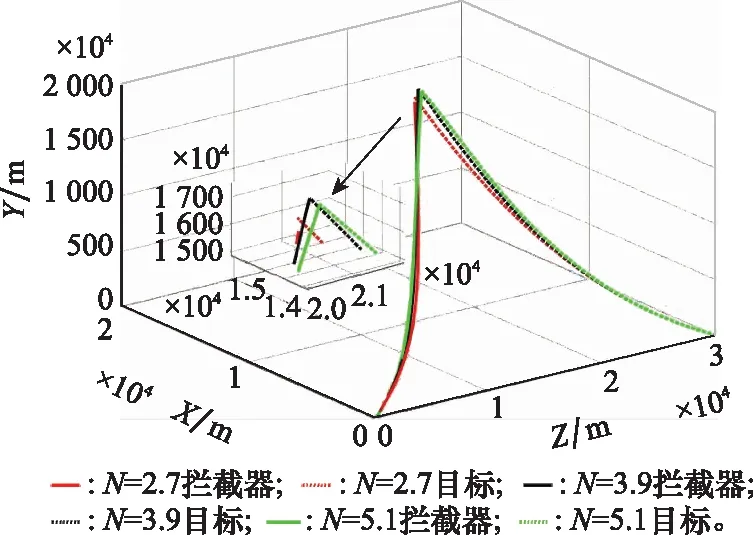
图9 情形3下的拦截轨迹Fig.9 Interception trajectory in case three

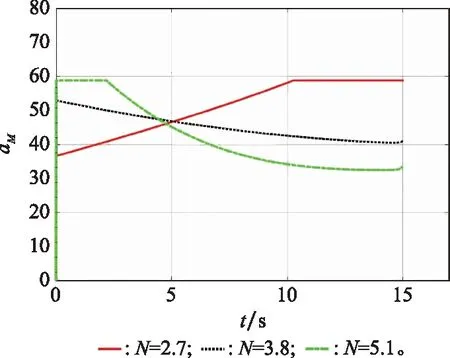
图10 情形3下的拦截器加速度Fig.10 Interceptor acceleration in case three

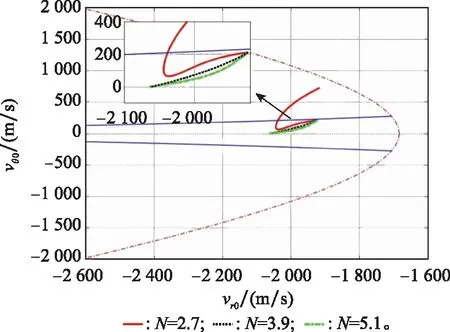
图11 情形3下捕获区域曲线Fig.11 Capture area curve in case three

从表5、图9和图10可得,取27时,拦截器未成功捕获目标,原因是拦截器在拦截后期过载受限,未能成功拦截;取3.9、5.1时,拦截器成功捕获目标,虽然后者在拦截前期过载达到饱和,但后期仍处于饱和过载以内,仍能够成功捕获目标。

对比图11与图5可得,在捕获区域内拦截低速目标和高速目标,速度变化趋势相似,即在选取合适的导航比时,速度状态总能趋近于零控拦截流形。再根据表1和表4可得,拦截低速目标和高速目标最大的差异在于容许碰撞速度的不同,其他条件不变时,拦截目标的视线接近速度越大,其容许碰撞速度相对越大。而由拦截器捕获目标初始距离和容许碰撞速度引起的捕获区域的变化也由第2节给出。

对比情形1和情形3可得,拦截低速目标情形与拦截高速目标在捕获区域内情形相似,从而证明了本文所推导的有限过载的三维现实真比例导引的捕获区域,对不同类型目标的适用性。

3.2 分析捕获区域影响因素

由式(44)和式(45)可知,该捕获区域的影响因素共8个参量,除去作为变量的初始视线接近速度、初始航向误差,其余6个参量均可在拦截前进行确定或者估计。下面将分析拦截器捕获目标初始距离、容许碰撞速度和容许脱靶量,拦截器饱和机动加速度,目标加速度在、方向上的机动加速度上限对于捕获区域面积的影响。

各影响因素对于捕获区域的影响将采用控制变量法分析。以表1中的数据为原始对比数据,以表6中的各行数据作为控制变量,来分别描述6个影响因素变化对于捕获区域面积的影响。

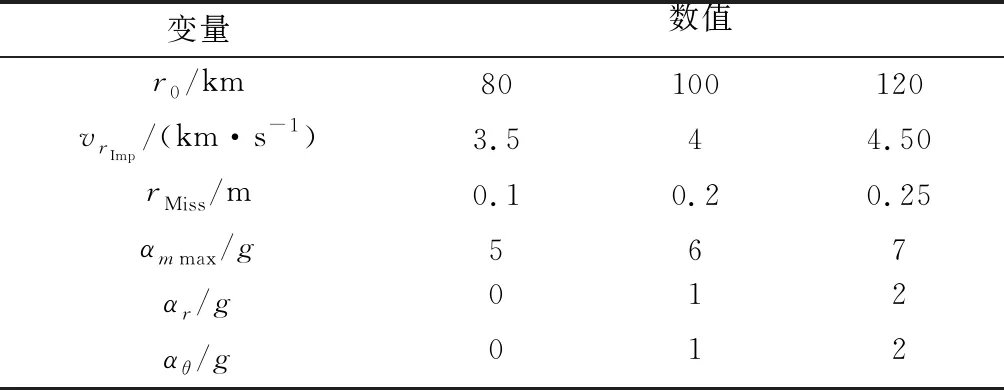
表6 单一变量变化时的取值

拦截器捕获目标初始距离分别取80 km、100 km和120 km时,捕获区域变化如图12所示,该距离的越大,拦截器与目标碰撞所需要的时间越长,由于目标在视线方向上存在朝向拦截器的加速度,造成捕获区域整体向左移动,但对视线接近速度位于捕获区域内的拦截器,其在捕获区域内初始航向误差范围增大,即拦截器能在更大初始航向误差范围内对目标成功捕获。容许碰撞速度由很多因素决定,是一个相对参考值,一般认为碰撞速度超过了容许碰撞速度,拦截器碰撞目标后,就能够摧毁目标。从图13中可以得到,容许碰撞速度主要决定了捕获区域的右边界,即容许碰撞速度越小,对捕获成功时视线接近速度的要求越小。从捕获的角度出发,容许碰撞速度在满足成功摧毁目标的前提下,被设计的越小越好。

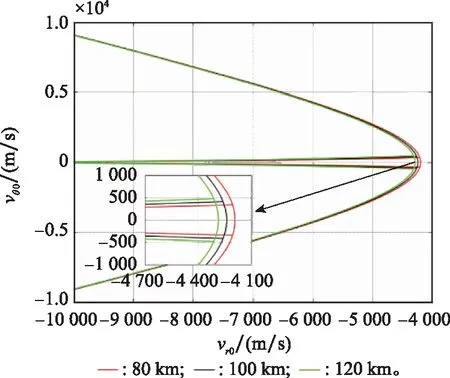
图12 拦截器捕获目标初始距离变化时捕获区域Fig.12 Interceptor captures the region when initial distance of target changes

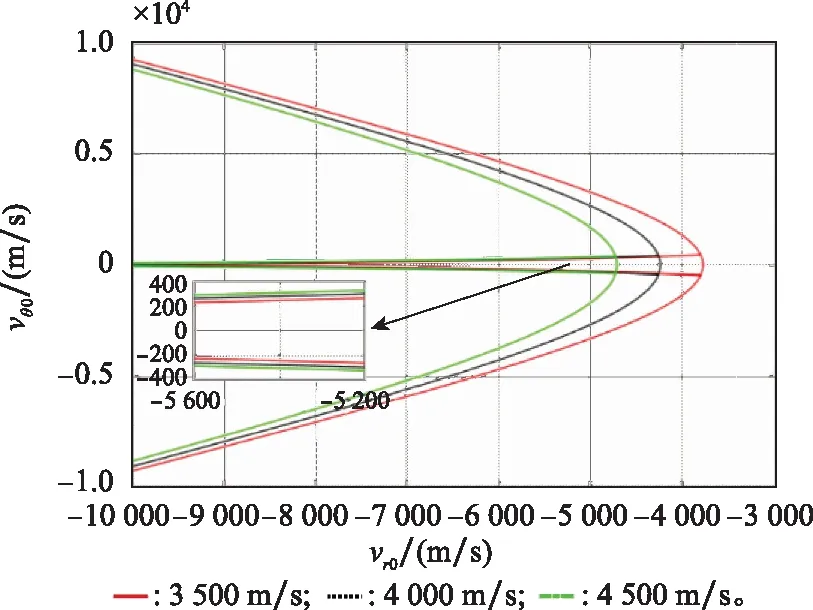
图13 容许碰撞速度变化时捕获区域Fig.13 Capture region when allowable collision velocity variation

容许脱靶量由拦截器的杀伤半径决定,由于该值相对于拦截器捕获目标初始距离过小,对于捕获区域的影响可忽略,所以在图14中容许脱靶量为0.10 m、0.20 m被0.25 m的图像所覆盖,该量对于捕获区域面积的影响可忽略不计,但在实际的拦截过程中,该值越小,对拦截器的命中精度要求越高。

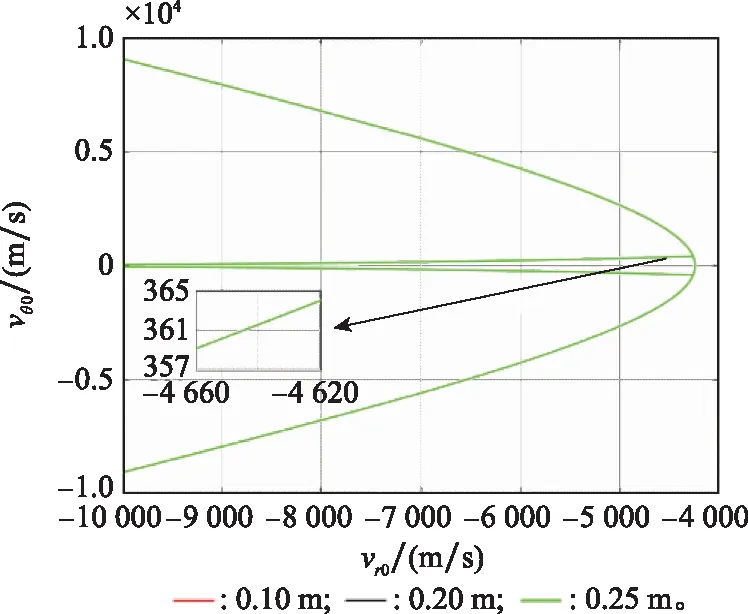
图14 容许脱靶量变化时捕获区域Fig.14 Capture region when allowable miss distance variation

从图15可得,拦截器饱和机动加速度对捕获区域的右边界没影响,只影响捕获区域内初始航向误差的范围。从拦截器的角度出发,对于相同初始视线接近速度,拦截器饱和机动加速度越大,捕获区域内初始航向误差取值的范围越大,越有利于成功捕获目标。

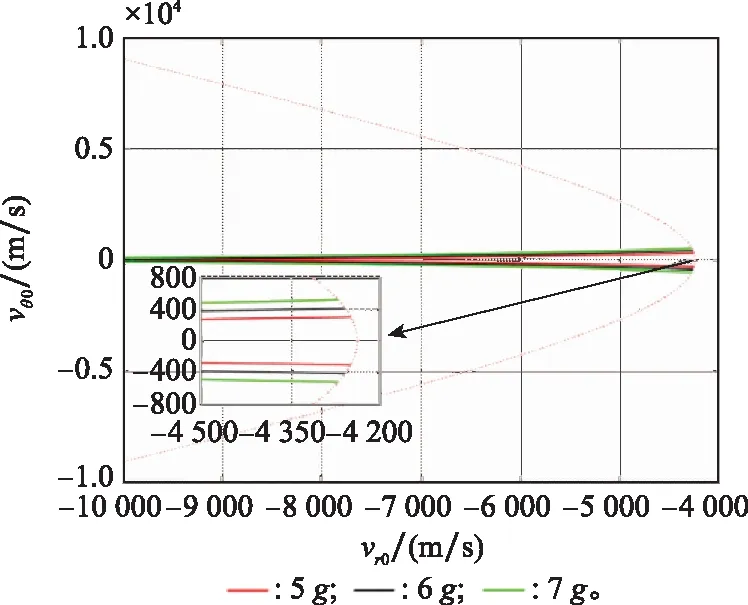
图15 拦截器饱和机动加速度变化时捕获区域Fig.15 Capture region when interceptor saturation maneuvering acceleration changes

目标在上的加速度上限影响了捕获区域的右边界和捕获区域内初始航向误差,由图16可得,该加速度越大,目标进行的机动对于视线接近速度影响越大,导致在捕获区域内初始视线接近速度的取值范围越小,捕获区域左移,进一步导致捕获区域的面积越小,对目标的捕获难度越大。

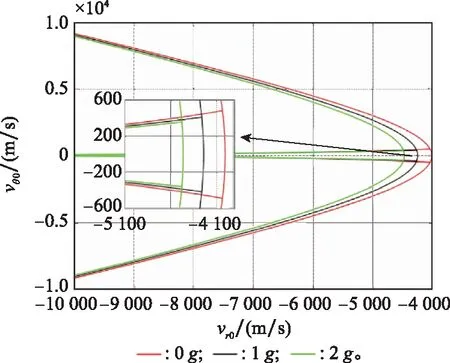
图16 目标在er上的加速度上限变化时捕获区域Fig.16 Capture region when the upper limit of the target’s acceleration on the er varies

从图17可得,目标在上的加速度上限对捕获区域的右边界没影响,只影响捕获区域内初始航向误差的范围。从捕获的角度出发,该值越大,捕获区域内初始航向误差的范围越小,越不利于成功捕获目标。对比图15可知,其影响与拦截器饱和机动加速度的影响相反。

从本小节分析可得,在拦截器与目标机动过载受限,在初始视线接近速度相同时,从拦截角度出发,拦截器捕获目标初始距离越大、饱和机动加速度越大、容许碰撞速度越小,拦截器越有利于成功捕获目标;从目标角度出发,目标的机动加速度越大、被拦截器捕获的初始距离越小、越不易被破坏越有利于突防。

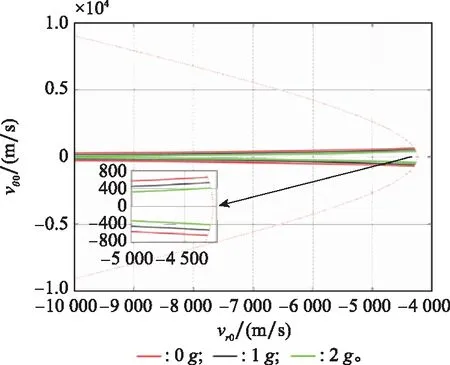
图17 目标在eθ上的加速度上限变化时捕获区域Fig.17 Capture region when the upper limit of the target’s acceleration on the eθ varies

4 结 论

本文基于视线旋转坐标系的相对运动模型,利用Lyapunov第二方法证明了视线旋转角速度Lyapunov稳定,然后通过反证法,得到了有限过载的三维RTPN拦截有限三维机动目标的捕获区域,为中末制导交接班时刻的条件约束设计提供了理论支撑。

本文提出的捕获区域是以拦截器与目标在视线旋转坐标系上的相对速度差作为坐标系,在二维平面内,本文结论在目标机动加速度任意且有界、方向垂直于弹目视线的假设条件下,与以前的结论一致,但本文结论适用于三维拦截,对于目标的加速度的形式没有特定要求,仅需预知目标三维机动加速度上界,若存在合适的导航比,就能保证在拦截器的饱和机动过载范围内成功捕获目标,能够适用于现实的拦截场景。对于捕获区域影响因素的分析,对拦截器的性能的设计以及目标的拦截和突防提供理论指导,具有一定的工程指导意义。