例谈学生发现数学问题能力的培养

曹悦

[摘 要]问题是让人探究数学规律的根本动力，教师要让学生具备发现并提出有价值的问题的能力。在课堂上，教师要营造适合学生提问的氛围，创设开放的、学生可自由提问的情境;要引导学生沿着问题的诞生路径思考，站在解决现实问题的角度提问;要因地制宜、因势利导，传授恰当的提问技法;培养学生的质疑能力，让学生明白何时质疑、怎么质疑。

[关键词]提问;问题情境;质疑

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）02-0090-03

学者布鲁巴克曾说：“精湛的教学艺术遵循的准则就是让学生自己提问题。”我国也有一句俗语：“授人以鱼不如授人以渔，授人以渔不如授人以欲。”后半句的意思比前半句更进一步，教给学生学习方法还不够，激励学生寻找或创造学习方法去汲取知识解决问题是更高一层境界。笔者在教学中十分注重培养学生的问题意识，让学生进行创造性学习，活学活用各种学习方法，全面提高学生的综合素质和数学核心素养，成为会学数学的人。

问题是让人探究数学规律的根本动力，没有问题和对问题的好奇心与探究欲，就不会有深层次的逻辑严密的理性思考和推理。在数学课堂上，如果只有教师提问，那么学生的思维是被动的，所有的思维痕迹都是短浅的，不会留下深刻印象。而学生观察分析后提出的问题，会让他们产生解决问题的动力，产生对数学的求知欲和数学化的思维模式。

培养学生的问题意识和解疑能力，使学生形成健全的数学理论研究谋略，具备提问的动力、敢问的勇气、发问的技巧、答问的智谋，是数学教学的目标。

一、提供机会，培养学生提问的能力

学生的提问能力不是凭空产生的，需要教师一步步诱导和培养，所以教师在课堂上要营造适合学生提问的氛围，创设开放的、学生可自由提问的情境，给学生提供提问的机会。学生提出的问题可能略显幼稚，或毫无价值，甚至有的学生会明知故问，但教师也应给予肯定和嘉许，呵护学生提问的热情，只有在这样轻松的环境中，学生才会大胆提问，不会因为担心被批评而不敢提问。

【例1】创设学生可自由提问的情境。

师：某小区举行“科学常识”竞答比赛。答题情况如下表。

师：哪一栋居民的答题情况好？你准备怎么分析这个问题？

生1：我是直接比较各楼栋答题成绩为优秀的人数，根据成绩为优秀的人数判断哪一栋居民的科学常识更加过硬。根据表格数据，2栋居民答题成绩为优秀的人数最多，有24人，而3栋居民答题成绩为优秀的只有19人，是3栋楼中最少的。

生2：每栋楼的参赛人数不一样，所以直接比较各楼栋答题成绩为优秀的人数不公平。

生3：我们可以比较答题优秀率。

笔者通过创设问题情境，让学生充分思考，有学生想到直接比较成绩为优秀的人数，有学生对此提出异议，然后有学生提出可以比较答题优秀率，那么就自然而然引出求答题优秀率需要通过百分数的计算来实现，学生的学习目标就自然转移到百分数上，学生会提出“哪栋楼居民的答题优秀率最高？”等问题。学生的思维一旦开放，很有可能在此基础上联想、发散，提出新的问题，如该小区可建立多维评价机制，不只统计优秀率，还可统计参与率、合格率、达标率，对各项指标进行评分再综合评价，这样才能客观公正地比较出各楼栋居民科学常识水平的高低。

教师可在问题情境中出示表格，指引学生根据表格数据提问，学生的思维就会由消极应对变为积极创造。尽管学生会提出一些简单的问题，没有达到教师的预期，但这些简单的问题会起到抛砖引玉的作用，能力强的学生会步步紧跟，不断在竞争中提出含金量高的问题，而且也会因为要对自己提出的问题负责，在构思问题的同时已经思考过解决问题的方法，其他学生也会更加关心问题的合理性和规范性。这样，学生的思维会在自由开放的氛围中更加活跃。

另外，教师还要适当改编课本的习题，制造提问的机会。例如，可以设计开放性问题“你还能提出哪些数学问题？请提出问题并解答。”这无疑为学生提供了创新的舞台，自问自答大大降低了数学问题的复杂度和学生答题时的局促感，学生可以按照自己的想法编写难度适中的问题。

二、提高问题质量，不信口开河

学生敢问了，但是他们提的问题可能只是机械地模仿，不走心，想起一出是一出。一些学生喜欢模仿，由于他们没有深入钻研问题，对问题的本质没有清醒的认识，可能会根据一些粗浅的运算经验提出一些不合时宜的问题，有些问题看似与数学相关，实则虚有其表。

例如，对情境“医生给急诊病人测量体温，病人A的体温是37.8℃，病人B的体温是39.4℃。”学生提出的问题有：（1）病人B的体温比病人A的高出多少？（2）病人B的体温和病人A的体温一共是多少？显然，问题（2）求两个人的体温之和毫无意义，这种问题的实际价值为0。

而有些问题的价值则要视具体情况而定，例如，对情境“住院1个月后，病人B的体重下降到34千克，病人A的体重比病人B的多4.5千克”。学生提出的问题有：（1）病人A的体重是多少？（2）病人A和病人B一共有多重？學生提出的问题（2）是求两人体重之和，但笼统求和是没有实际价值的，求和要在特定情境下才有用，比如两人就医时，同乘一辆救护车，而救护车的载质量是固定的，这时求体重之和可以判断救护车是否超载。

学生之所以会提出一些违背常理的数学问题，是因为其抽象思维受到限制，本来数学问题是从生活情境中抽象出来的，但是因为惯性思维，学生见到同一类型的数据，就容易想当然地提问，这样的提问其实是学生事先想好答案的，但是一旦考虑现实情境，会发现问题其实是行不通的，起码在客观上行不通，就像将两人的体温相加是没有任何现实意义一样。要避免理论与现实不符的提问，唯一的办法就是回归数学本质，让学生沿着问题的诞生路径重新思考，站在解决现实问题的角度来提问，而不是站在理论上可行的角度提出一个无法成立的问题。

【例2】让学生站在解决现实问题的角度提问。

师：医院治愈了3个病人，病人A的医疗费是2350元，病人B的医疗费是2500元，病人C的医疗费是3620元。你能提出哪些问题并解答？

生1：病人A的家属预付医疗费3000元，办理出院手续时，医院应退回多少钱？

生2：病人B的家属预付医疗费3000元，办理出院手续时，医院应退回多少钱？

生3：病人C的家属预付医疗费3000元，办理出院手续时，医院应退回多少钱？

师：生3提出的问题有些行不通，有人知道为什么吗？

生4：老师，我不是很明白，同样是预付了3000元，求医院退回的钱数，为什么前两个问题行得通，第三个问题行不通呢？

师：病人C的医疗费与病人A、病人B的医疗费有什么不同？和3000元比较一下。

生5：病人A、病人B的医疗费低于3000元，病人C的医疗费高于3000元，如果病人C的家属预付医疗费3000元，那么不应该求医院退回多少钱，而应该求病人C要补交多少钱。

三、讲究方法，让学生问得巧妙

学生想根据已知的数学信息提问，但是不知如何开口，也不知如何发问，提出的问题往往偏离数学轨道。要么所言非所想，词不达意，要么问题过于简单，让人一眼看穿，因此教师要因地制宜、因势利导，传授恰当的提问技法。

【例3】创设情境，传授提问方法。

师：已知某医院现在住院的患者中男性有1000人，女性有1200人，根据条件自由提问。你能提出用加减法求解的问题吗？

生1：我可以提出问题“男性患者比女性患者少几人”。

师：有没有同学能提出用乘除法求解的问题。

生2：我可以提出问题“男性患者的人数是女性患者的人数的百分之几”。

师：有什么问题可以用两级运算求解的？

生3：我可以提出问题“男性患者的人数比女性患者的人数少百分之几”。

将这种练习常态化，学生就会积淀一定的提问技巧和经验，提问时就会有的放矢，提出有层次、有水平的问题。

学生的提问水平与其知识结构息息相关，如果学生的知识结构过于简单，那么学生只能提出基础的问题，如“一共有多少”“谁比谁多多少”，但凡需要一点技巧的问题，学生根本想不到，因为掌握的知识不多。如果学生全面学习了分数，掌握了分数的意义和性质，就可以提出用除法来解决的问题，这个除法又不同于低年级的“等分除”和“包含除”，而是分数意义层面上的“求一个数是另一个数的几分之几”，完成一次知识的升华。学生还可以融合加减法和除法，提出“一个数比另一个数多几分之几”之类的问题，或者直接提问“一个数比另一个数多百分之几”，这样就将减法、分数与除法的关系、百分数与分数等知识整合到一起。

四、教师引导，合理质疑

培养学生的质疑能力绝不是让学生无端挑刺，没事找事。何时质疑，怎么质疑，需要教师的细心引导。下面以“扇形统计图”教学为例说明。

1.课前提問，明确方向

问题意识是创新的源泉，课堂教学要想高效，就要专攻学生的知识盲区，勘测出盲区在哪里。首先，教师要引导学生找出新知与旧知之间的缝隙，也就是在新旧知识衔接处找缺漏。虽然许多新知是旧知的延续，但是其中有脱节、断带的地方要修补。因此，每次教学新知前，笔者都要设计课前质疑环节。在教学“扇形统计图”一课时，笔者先让学生回顾条形统计图、折线统计图，以及它们各自的特征，然后揭示本课课题“扇形统计图”，引导学生思考：“关于扇形统计图，你想从哪几个方面研究？”学生很快心领神会，提出“扇形统计图是什么样子的”“扇形统计图和其他统计图有什么区别”“扇形统计图的特征是什么”等问题，这些问题的提出为学生找到了学习的目标与方向。

2.课中提问，提升认识

【例4】用习题引导学生学会质疑。

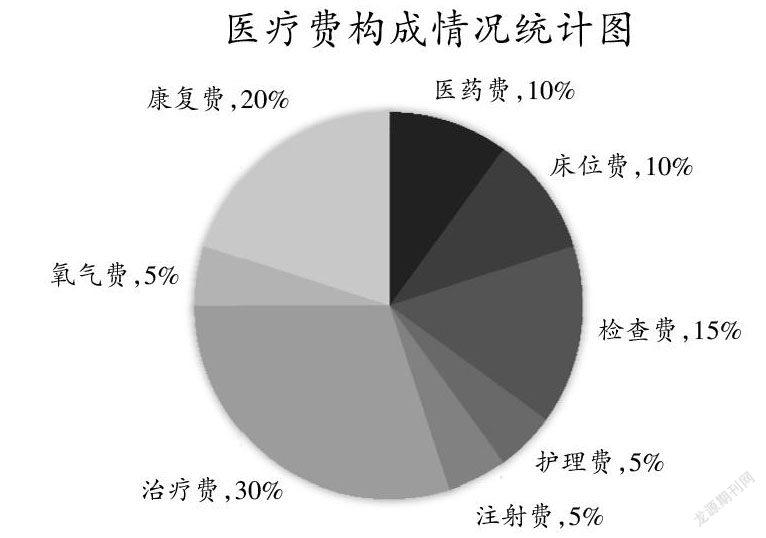
师：上图是某病人的医疗费构成情况统计图，已知该病人此次医疗费合计2500元。请同学们思考问题——（1）哪项费用支出最多？支出了多少元？（2）检查费是多少元？

（学生思考并回答）

师：你们还能提出哪些问题？

生1：我可以提出问题“支出医药费多少元”。

生2：我可以提出问题“共支出治疗费和检查费多少元”。

生3：我可以提出问题“医药费比检查费少多少元”。

（教师让学生解答这些问题）

师：看到这张统计图，你能联想到哪些社会信息？还能提出什么问题呢？

生4：医保可以报销部分医疗费，我可以提出问题“假设医保报销比例为80 %，该病人可以报销多少医疗费”。

学生的提问大致分为三类：生1根据一条信息提出一步解决的问题，是模仿教师给出的问题（2）出题;生2是综合考虑两条信息提出用加法解决的问题;生3是综合考虑两条信息提出用减法解决的问题。通过让学生提问并解答，学生对扇形统计图有了深刻印象。但笔者并不满足于此，而是引导学生联系生活实际继续提问，生4马上想起“医保可以报销部分医疗费”，据此做了假设后提出问题，此外，还可以让学生在课后查阅有关文件资料，根据实际情况提出更多问题。

只要教师在课堂教学中始终为学生着想，时刻想着充分发挥学生的主观能动性，让学生自己发现问题、设计问题，并大胆想象、细心求解，学生的数学素养必定会全面提升。

[ 参 考 文 献 ]

[1] 古智深.在比较和对比中培养学生发现并提出问题的能力：以“梯形面积公式推导”为例[J].小学数学教师，2020（04）.

[2] 陈云.对“发现问题”和“提出问题”的一点认识[J].教育研究与评论（小学教育教学），2020（03）.

[3] 朱国荣.“求学问，需学问”：落实“增强发现和提出问题的能力”之思考[J].教学月刊小学版（数学），2018（Z1）.

【本文系安徽池州市2020年度教育教学研究课题“基于网络资源平台下小学数学混合式教学实践探索”的研究成果，编号：JK2022。】

（责编 杨偲培）