SOLO分类理论在小学数学深度教学中的应用研究
2022-03-11胡锦洪
胡锦洪


[摘 要]SOLO分类理论是一种量的测评与质的考查相结合的评价理论,它能有效帮助教师了解学生思维发展的水平和层次,改进教师的教与学。运用SOLO分类理论指导教师准确把握学生五种结构层次对应的数学思维水平表征,能实施精准教学并及时跟踪评价,发展学生数学思维水平,促使课堂教学走向质的提升。
[关键词]SOLO分层理论;深度教学;数学思维
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)02-0015-03
笔者认为深度教学的本质就是促进学生高阶思维能力的发展,让不同学生的数学思维水平得到不同程度的发展,实现有价值的学习。为此,笔者运用SOLO分类理论指导教学,寻求有效的路径与方法。
一、SOLO分类理论指导教学的认识及启示
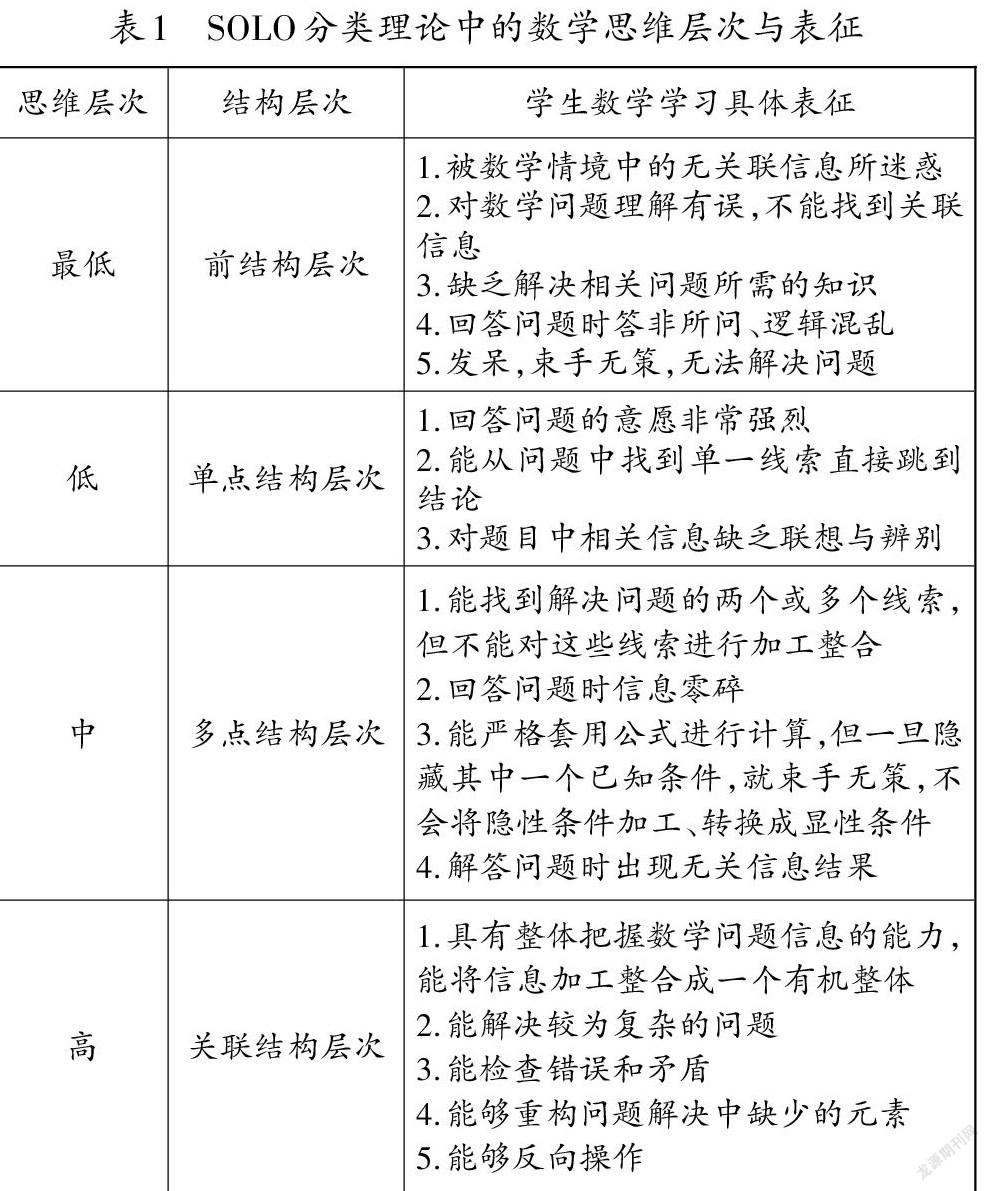
SOLO分类理论,其中“SOLO”原意是“观察到的学生学习结果的结构”。SOLO分类理论用结构特征来诠释学生反应,并且对照学生特定反应的表征方式来确定学生学习结果的层次。SOLO分类理论将学生学习结果分为五个层次,即前结构层次、单点结构层次、多点结构层次、关联结构层次、抽象拓展层次。依据数学学科特点,笔者将这五个层次的具体表现整理如下:
根据SOLO分类理论,课前对学生已有的反应水平进行前测,从而把握学生已达到的知识经验水平,找到学生的最近发展区,指导教师设计并制订适当的课时教学目标(学生在某种特定学习任务上的逻辑终点)。
2.把握五個结构层次之间的联系,指导学生思维发展循序渐进
学生五种水平反应的表征,在教学过程中是层层深入、螺旋上升、重复出现的,也是学生思维水平从低阶走向高阶的过程。五个结构层次相互联系,在教学中表现出课堂教学过程的完整性,而不是直接奔向答案的教学。
3.评价学生问题反应的水平,指导和改进教师的课堂教学
不同学生的反应水平有助于教师的具体指导与评价,进而促进学生的思维水平表征更加结构化、清晰化,也促进教师反思与改进教学。
二、SOLO分类理论在深度教学中的实施策略
SOLO分类理论指导下的深度教学,基本环节包括课前对学生思维发展水平的把握,使教学目标贴近学生思维的最近发展区;教学过程中抓住数学核心要素(学科本质),让学生经历五种反应水平的不同过程,促进学生思维水平朝高阶发展;学生学业质量评价与教师教学目标达成情况要针对学生五种不同反应水平实施精准评价并提供相应的指导策略,促进学生完善自我认知及发展学业水平个性化。
(一)SOLO分类理论的前测内容及结果分析
前测的目的是了解学生的数学思维水平,制订适当的教学目标,使学生的学习贴近最近发展区,促进学习深度发生。
1.前测内容:抓住学科本质,发展高阶思维
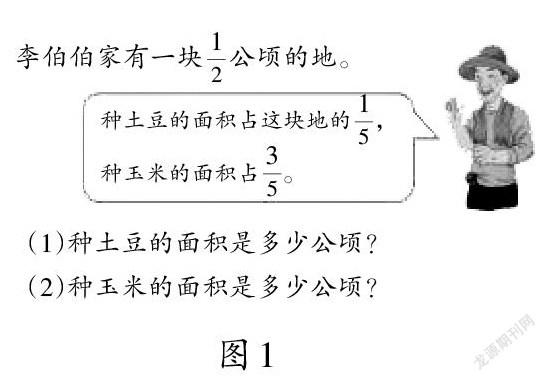
核心内容的确定不仅要有助于让学生掌握基本知识、技能与方法,还要有助于促进学生积累数学活动经验、感悟数学思想、提升思维水平。如“分数乘分数”的一道例题(如图1),测评点在知识技能方面是学生能否正确计算分数乘分数,在能力思维方面是学生能否通过多种表征理解乘法算式的含义、理解分数乘法的算理和算法,并在不同情境中运用算法,不断积累数学活动经验,抽象概括运算法则,建立模型。
2.结果分析:五种反应水平,提供教学建议
笔者以“分数乘分数”为例,运用SOLO分类理论确定了五种学生反应水平,并对我校六年级(3)班学生进行了相应的评价测试。
(1)测查的结论
统计样本是我校六年级(3)班学生,共40人。对学生的解答进行了归类与统计,SOLO分类理论各层次的人数与占比情况如表2。
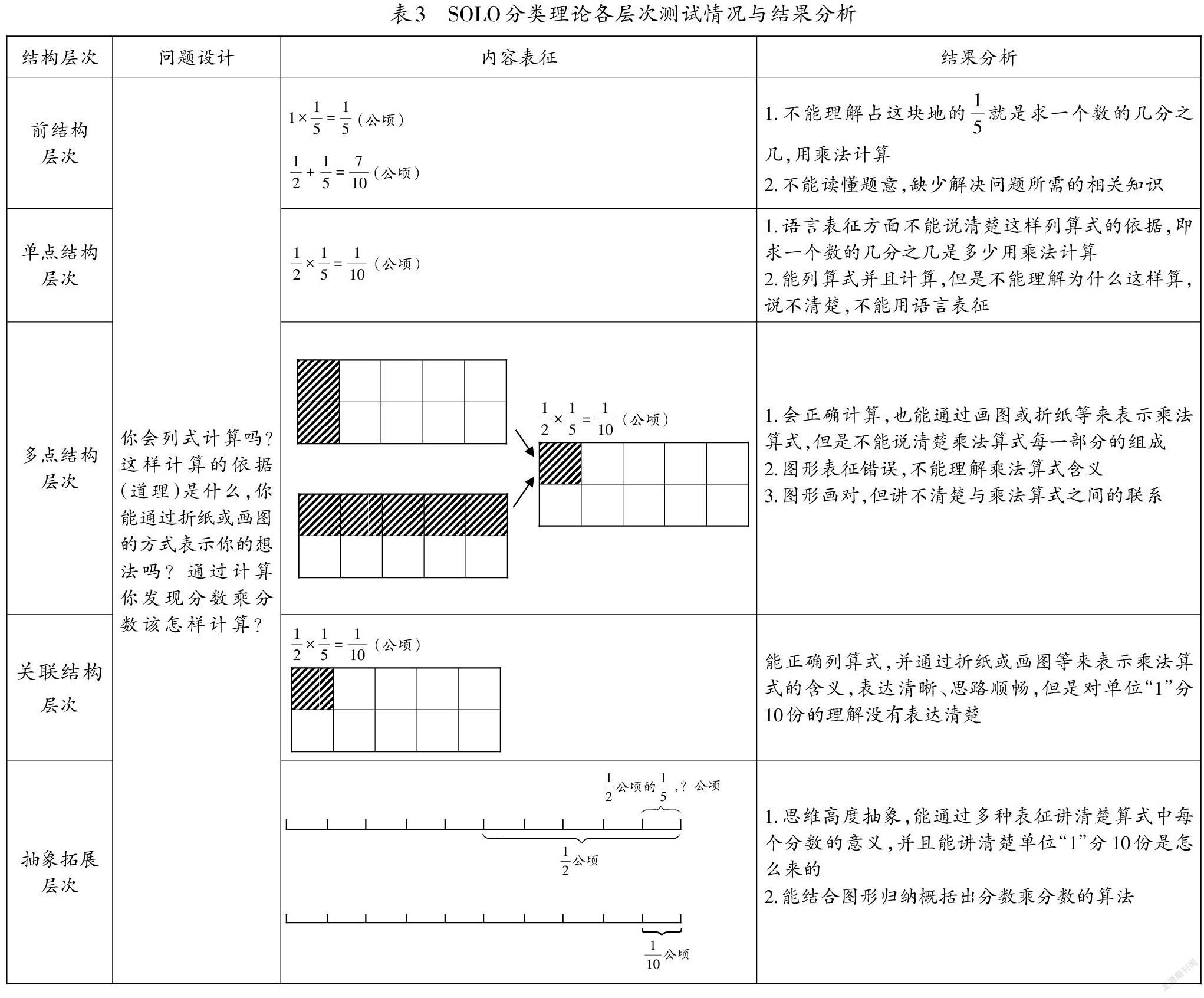
(2)测试内容与分析
对以上测试情况,结合具体内容表征对问题(1)的回答情况展开分析,如表3。
(二)SOLO分类的课堂教学实施对策
针对以上测试情况及结果分析,在“分数乘分数”的教学中,笔者确定了如下教学对策。
1.前结构层次、单点结构层次的学生向多点结构层次提升
通过重视学生搜集、整理数学信息的全过程,促使学生形成认真审题、分析数量关系、动手操作的习惯,同时积累感性认识,丰富数学活动经验,使学生从前结构层次、单点结构层次走向多点结构层次。
(1)重视整理数学信息,理解题意
通过前测笔者发现,65%的学生在前结构层次和单点结构层次主要表现为不理解题目意思或急切作答,忽视审题、读取信息和整理数学信息。因此,教师要重视学生审题意识的培养,数学信息的搜集与整理也不容忽视。
(2)重视梳理数量关系,正确列式
前结构层次、单点结构层次的学生虽然列式对了,但笔者追问这样列式的依据,学生却不能讲清楚数量关系。因此梳理数量关系的教学十分重要。就“分数乘分数”这节课,[12]×[15]的列式依据是求占这块地的[15]是多少,就是求[12]的[15]是多少,也就是求一个数的几分之几是多少,用乘法解决。这里用到的知识点就是“求一个数的几分之几是多少”。
(3)重视动手实践操作,积累经验
前结构层次、单点结构层次的学生不能通过动手折纸或者画图来表示乘法算式的含义、理解分数乘法的算理和算法。教师要重视算理的教学,加强学生的动手操作,丰富学生的数学活动经验。教学中,教师要提供丰富的数学素材,给予学生足够的时间经历观察、实验、探讨、辨析、论证等学习过程,促使学生从机械的学习走向有意义的深度学习。
2.多点结构层次的学生向关联结构层次提升
学生从面对数学信息时的慌乱无措到能系统有条理地整合,并能结合图文等方式用语言完整地表达出来,这是向关联结构层次提升的重要标志。
(1)重视图文表征,理解乘法算式的含义
结合图文等表征,能讲清楚乘法算式的意义。如[12]×[15]=[110]这个乘法算式,根据多点结构层次的内容表征,学生要清楚表述[12]是指把一张纸看成1公顷,平均分成2份,每份就是[12]公顷。[12]×[15]表示把[12]公顷平均分成5份,取其中的1份。最后阴影重合部分的1个方格也就是把1公顷(整张纸)平均分成10份,取其中的1份,就是[110],即[12]×[15]=[110]。
(2)重视语言表达,提升抽象思维的水平
走向关联结构层次的关键训练点就是有条理地表达,要重视学生语言的训练。在教学中,笔者发现学生语言表达的难点在[12]×[15]与[110]的沟通联系。表达[12]×[15]重在如何平均分、如何取,而表达[110]重在单位“1”的转化,即1份相当于整张纸(1公顷)的十分之一。学生结合图形演示,将自己的思维过程有步骤地表达出来,思维水平从形象向抽象过渡。
3.关联结构层次的学生向抽象拓展层次提升
重视学生多元表征,揭示分数乘分数的数学实质,学生在归纳概括中,提升数学思维水平。
(1)重视多种表征,深刻理解单位“1”
笔者鼓励学生用不同的方法表征想法,从而揭示不同表征背后的数学实质。例如,除了用长方形来表示,有的学生还用线段图来表示。笔者请学生表达自己的思考过程,最后概括提炼:[12] × [15]表示把[12]公顷平均分成5份,取其中的1份,也就是把1公顷平均分成(2×5)份,取其中的1份,即[12×5]×1=[1×12×5]。
(2)重视归纳概括,建立数学思维模型
提升到抽象拓展层次,关键是要抓住学科本质,建立数学模型。教学中,教师要引导学生归纳概括,得出分数乘分数的运算法则:分数乘分数,用分子相乘的积作分子,用分母相乘的积作分子,能约分的要先约分再计算,最后的结果要用最简分数表示。
本研究在教学中使用SOLO分类理论,主要研究方向是单元教学的种子课,聚焦教学重点,突破难点,发展学生数学思维水平。SOLO分类理论的运用给笔者的启示:重視课堂里学生的动手操作活动,丰富学生数学活动经验;重视学生数学语言的表达、归纳与提升等。SOLO分类理论在深度教学中的应用研究,还需要教师继续实践与完善。
(责编 吴美玲)
