一道习题两个答案的背后……
2022-03-11王永生
王永生

[摘 要]习题是训练学生思辨力的主阵地,能帮助学生提高数学阅读能力。教师在指导学生解决问题的过程中,要事前作好规划和决策,总揽全局,科学筹划,培养学生的审题能力和分析能力,这样才能提高学生解决问题的能力。
[关键词]数学;审题;计费;服务;流量;追及;最少
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)02-0021-03
筆者在一篇文章中看到一道题目:
中国电信公司为了拓展5 G网络业务,特推出两种优惠方案,具体预案如下表。
当天翼手机用户每月上网流量最少是多少时,两种方案收取的费用相等?
学生解答该题时,出现了两种不同的思路和两个答案。
一种思路是计算两种方案保底消费的差价可支付多少超额流量:60-40=20(元),20÷0.2=100(G),100+60=160(G)。通过检验对比发现该思路的答案是正确的。
另一种思路则是采用设未知数列方程解应用题的方法,直接设未知数,然后根据题干中两种方案收取的网费相等作为等量关系来列方程:设每月上网流量最少为x G时两种方案征收的流量服务费相等,因此,40+(x-60)×0.2=60+(x-200)×0.3,解得x=280。通过检验所列方程和所求解,发现居然也是正确的。
为何会出现两个不同的答案?而且两个不同的答案居然都正确。对于这道题来说,正确答案只会是其中之一,那么是哪个呢?
一、在对比检验中找出多解原因
原文作者引导学生继续讨论,通过方方面面的对比,最后找到了原因:发现未知数x是上网流量,这个流量可能大于200 G,也可能少于200 G,第二种思路是用方程法解,其列式默认流量比200 G多,因为两边都减去了保底消费固定流量,所以此处的实际使用流量默认大于200 G。而两种方案都涉及分段收费,也就是月结算使用流量未超出保底流量时,统一收取定额费用,因此还存在介于两个保底流量之间的使用量,其中一种方案按照保底消费收费,另一种按照分段计费,所以还应该列出一个流量比200 G少但是比60 G多的方程,即设每月流量最少为x G(60在这种情况下,即在流量达到160 G时,方案一使用了100 G的超标部分加收的流量费20元,再加上方案一的保底消费40元,共计60元,而这个实用额度160 G在方案二中属于保底范围,也就是说160 G还在每月固定流量200 G内,需要缴纳的流量费仍属于保底消费60元,此时在方案二下是一个恒量,与未知数x的大小无关,况且题目问的是“当天翼手机用户每月上网流量最少是多少G时,两种方案征收的费用相等”。题中出现了“最少”,这是一个极易被忽略的关键词。因为这个关键词的存在,所以还要在两个可行答案里做一番筛选,去掉较大的值,也就是280 G,而保留160 G作为最终答案。因此,该题的答案应该是160 G。
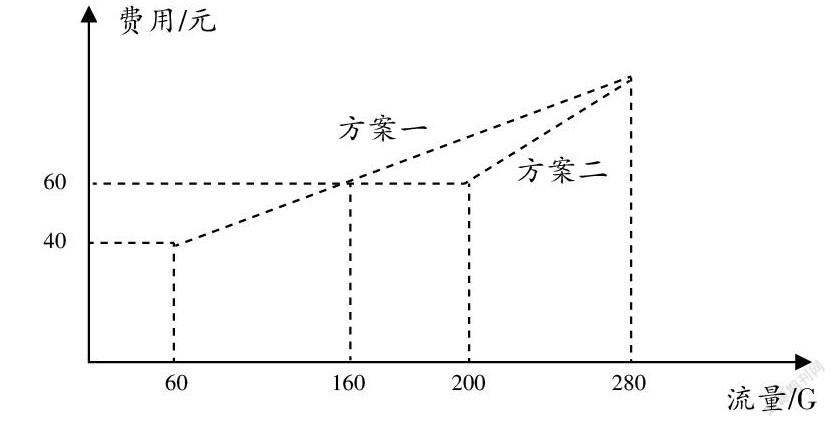
此类问题,比过去单一的分段计费问题更加复杂,因为增加了另一种收费方式,两种收费方式都是分段的,而且分段区间是错开的,学生很难兼顾到两种方式的动态变化。实际上,这类题的难点在于,未知数到达某个值时,其中起步价高一些的计费模式处于静止定额状态时,另一种模式已经启动加收程序。如方案二流量在200 G以内费用固定为60元,而将这个60元作为方案一的收费,则会计算出一个新的流量数,此时,二者相等其实是固定方案二的起步价而等待方案一的追平。但是,在两种方案同时达到60元额度、流量达到160 G后,方案二的费用还要维持60元一段时间,而此时,方案一已经开始持续低速上升,方案二达到200 G保底额度后,才开始高速追赶,最后动态追平方案一的收费。转换成统计图如下:
二、类比迁移到“追及问题”的缺陷
之后原文作者又借题发挥,类比迁移到“追及问题”中,把该问题比拟成追及问题:两名跑步选手本身就拉开了一段距离,快者在前,慢者在后,一开始行进速度快者原地不动,行进速度慢者追上行进速度快者(类比160 G),行进速度快者还是没动,行进速度慢者继续往前跑,等行进速度慢者跑了一段时间,到了行进速度快者起程的时间,行进速度快者才开始追赶进速度慢者,经过一段时间(类比280 G),行进速度快者追上了行进速度慢者,再之后行进速度快者和行进速度慢者都在跑,行进速度慢者就永远追不上行进速度快者了,也就没有第三次追及了。
笔者认为原文作者的迁移能力和联想能力非常高超,但是解题思路及决策路线存在瑕疵。
众所周知,在解决应用题时,首要任务就是审题,将题干中涉及的信息一字一字读清楚,不漏放任何一个细节和任何一个逻辑关键词。就本题而言,由于原文作者和学生在列方程时本身就审题不到位,忽略了题干中能够影响和左右解题思路和问题走向的关键词“最少”,这是一个逻辑关联词,限定了答案的范围,但是可惜被无视了。于是原文作者和学生就稀里糊涂得出两个答案,而且作了一番验算后,发现两个答案都是正确的,而且无懈可击、无法驳倒。他们没有用发展变化联系的眼光来看待两个答案,把它们看成是孤立存在的,从而引发了为什么会有不同但是都正确的答案的疑惑。
实际上,从该题“当用户每月上网流量最少是多少G时,两种方案征收的费用相等”中,就可以敏锐判断出无线流量服务费相等的流量节点至少有两个,否则逻辑关联词“最少”就是废话。而数学语言的凝练简洁告诉我们,这种决定问题走向影响解题大势的逻辑关联词是不会轻易出现的,事出必有因,所以当学生求得流量达到160 G时流量费相等,教师就应该敏锐觉察到此时的流量节点超过了方案一的固定流量,而没有达到方案二的固定流量。也就是说,方案一加收超额流量费后,方案二还是保底消费,也就是方案一的超额收费追平方案二的定额收费,而在前期双方都未达到节点时,发现方案一的收费无论如何都不可能与方案二的收费相等(40<60),此时就应该推断出160 G是首次追平的流量节点,那么还存在第二次追平,就是月使用流量超过方案二的固定流量(200 G)后,方案二的收费就会逆势上涨(因为0.3元>0.2元)。教师引导学生寻求流量费用相等的另外一个流量节点,这个流量节点预判出现在200 G后,再通过比较得出最少的流量节点,而不是在学生误打误撞得出答案后讨论为什么会有不同但是都正确的答案。这个问题本身就很幼稚,也容易误导学生,出现“一问两答”的尴尬局面。
由此可见,原文作者在指导学生解决问题时审题严重不过关且敷衍。如果按原文作者的做法,那么在学生独立解决该问题时,当求出一个流量费用相等的流量节点后就不可能再分析是否有流量费用相等的其他的流量节点,因为根据答案的唯一性,求出一个流量节点就算大功告成。毫无疑问,这不仅会让学生养成麻痹大意的习惯,还容易制造错解。
因为意外出现了两个答案,才引起教师的重视,去深入探究这个问题,但是这种探究其实是没有必要的,甚至将简单问题复杂化,这种复杂的双线变化问题,明显已经超纲,而且也不符合分段收费教学的真正目标定位。造成这种被动局面的原因是审题不严,教师没有把握好这类题目的关键命门。题中说到的“最少”其实已经指明了方向,学生只要对比分析出:方案一收费模式的基础额度低于方案二的,起步价也低于方案二的,而且增速也低于方案二的。如此一来,在方案一收费模式的增长阶段和方案二收费模式的停滞阶段,也就是60 G和200 G之间,必有一个交汇点,这个交汇点就是最小值,因为此时方案二是保底收费,只能是方案一去追平方案二的收费,而方案二的收费无法降至与方案一收费相等。
三、折线统计图的启用
笔者佩服原文作者丰富的想象力,在确定是否还有其他流量费用相等的流量节点时,脑洞大开地把该问题类比迁移成“追及问题”模型,从而让学生在直观的行程问题中类推揣摩,明白除了上面两个答案,绝无第三个答案的可能。
但是这种迁移类比是要以学生对追及问题烂熟于心为前提的,而教材没有单设这一内容,教材中只有行程问题中的相遇问题,鲜有提及追及问题,追及问题只是课后的拓展内容。如果学生对“追及问题”本身就一知半解,或者印象模糊,那么也就不可能想象出追及问题的情境。更何况课外教辅中追及问题的变形变式很多,很多编者将追及问题中的追及过程编写得曲折离奇,其过程复杂多样,所以笔者认为让学生通过追及问题来对照理解只有两个流量费用相等的流量节点还是有困难的。那么如何让学生明白流量费用相等的流量节点只有这两个呢?笔者认为折线图是首选。
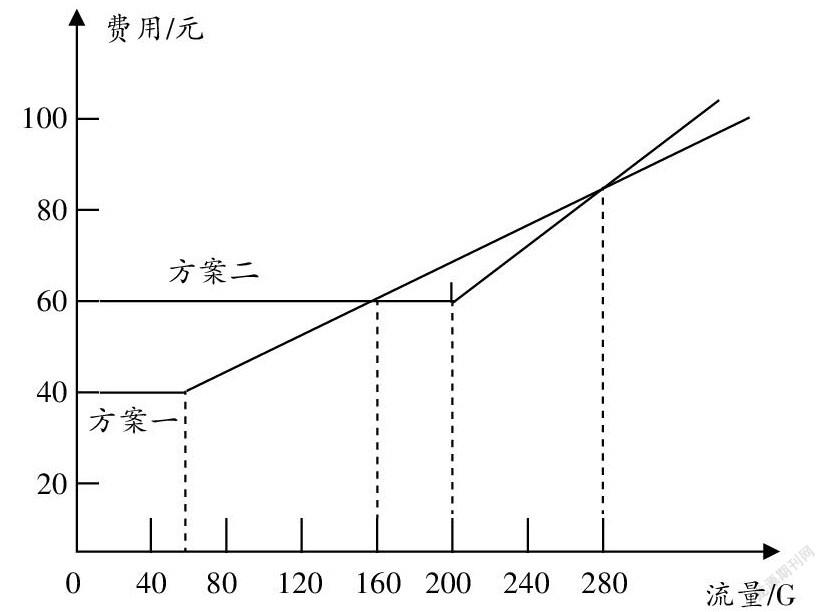
观察分析折线图可以直观地发现:表示方案一的折线与表示方案二的折线在160 G和280 G这两个坐标处汇合。对照纵坐标可以看出,这两种方案在160 G和280 G时流量费用相等,第一次是60元,第二次高于60元。流量超过280 G后,两条折线的差距越拉越大,从趋势上看渐行渐远,不可能再交汇,所以流量费用相等的流量节点只有两个。
通过复式折线图还容易看出流量少于160 G时,方案一的流量费用一直少于方案二的;流量处于160 G和280 G之间时,方案一的流量费用反超方案二的流量费用;流量多于280 G时,方案一的流量费用又处于劣势,方案二的流量费用逆势而上。两种方案费用的对比“反转再反转”,所以作为天翼手机用户,如果每月流量少于160 G或多于280 G,选择方案一比较划算,而流量恰在160 G与280 G之间,那么选择方案二比较划算,这样不仅保留原有情境,还让学生在回顾和起用旧知复式折线统计图的同时,进一步体验到复式折线统计图能反映多组数据对比高低和变化趋势的特性,逐渐形成分类讨论和分段計费思想以及数形结合的思想。
将收费问题转化成追及问题,似乎只有通过折线统计图才能展现出来,这种直观的手段可以很好地揭示出两个变量的对应关系,但是如果从问题本身的角度出发,这种做法似乎又增加了思考难度,因为学生必须清楚地理解数量关系才能成功绘制出复式折线统计图。而绘制复式折线统计图的难点在于学生要相对准确地把握各个量的大致差距以及增长性收费的增长率,也就是折线的斜率,这些都需要学生对数据变化有敏锐的洞察力和判断力,而如果学生真有这种分析力,那么脱离折线统计图同样也能找到正解。
综上所述,习题是训练学生思辨力的主阵地,教师在指导学生解决问题的过程中,要事前作好规划和决策,培养学生的审题能力和分析能力,总揽全局,科学筹划,这样才能提高学生对问题的解决能力。
[ 参 考 文 献 ]
[1] 郑保华.小学数学“问题解决”教学的优化策略[J].数学教学通讯,2021(04).
[2] 刘春风.优化小学数学解决问题的教学策略[J].基础教育研究,2019(06).
[3] 苗培林.小学数学问题解决的优化策略[J].教书育人,2017(28).
(责编 吴美玲)
