基于俞正强老师对分数思考的再思考

周扬辉

（浙江省杭州市余杭区杭州二中树兰实验学校,浙江 杭州 311100）

俞正强老师在《“分数的认识”怎么教》这篇文章中认为分数的认识应该由量到率，再对比二者关系。这番思考引发笔者对这节课进行了深思，个人觉得前后两节课之间没有必然联系，第二节课相当于另起炉灶，全新阐述分数的概念，走的是两条平行线，两种概念并未相交。笔者认为分数概念的产生一定是基于整体与部分的关系，量与率的概念都应从分物的情境中产出，所以认为本节课应该量率结合同时进行。

一、现状分析，问题缘起

在小学毕业考试中分数是必考内容，出错率却居高不下。在调查中发现一线教师对此块内容相当重视，在教学中研发各种变式题，归纳解题技巧，可是依然没有明显的效果。原因是什么呢？不妨先看他们的问题所在，集中体现为如下两种题型：①比4 分米多是（）分米。②比4 分米多分米是（）分米。这组题目有很多人出错，而且呈现出年级越高出错率越高的趋势。在本校五六两个年级中进行抽样调查发现，五年级的错误率在34%左右，六年级的出错率在45%左右，个别班级数值更高。这就反映出学生对分数表示量与关系的含义混淆，尤其是涉及单位“1”是一些物体时，这种混淆情况更严重。

关于上述出现的问题笔者存在两个困惑，困惑一：学生为什么会出现量率不分的问题？困惑二：为什么问题是暴露在五年级？分数概念的学习是在三年级上册所处的学龄段进行的，那么两个学龄段之间有着怎样的联系，造成这个问题的根源是什么？

二、追本溯源之教材解读

原因之一：时间跨度大

人教版把分数知识编排在三个阶段：三年级上册第八单元《分数的初步认识》，五年级下册第四单元《分数的意义和性质》以及第六单元《分数的加法和减法》，六年级上册第一单元《分数乘法》以及第三单元《分数的除法》。从纵向的编排来看分数知识的编排时间跨度大，经过两年的时间学生对分数的知识还保留多少？这对概念体系的形成是很不利的，笔者认为这是问题暴露在五年级的因素之一。

原因之二：知识间呈现断层

从教材呈现的内容来看，三年级关于分数部分的编写通过创设分物的情境图引起学生“分”的实践活动。通过对单位“1”的平均分，认识并理解这样的几分之一的分数。并以此为基础再进一步认识分数。笔者认为分数由分物产生，但呈现在学生面前的不是分到物品的具体量而是分到的部分和整体之间的关系。接着几分之一的比较大小也通过图的比较，其实质也是量的大小的比较。分率和量就这样混搭着呈现给学生，而且量还是隐晦地呈现。三年级的学生能辨别到这两种含义吗？答案是否定的，笔者进行了一次尝试教学证明了此观点。

按照教材的编排第一课时直接认识分数关系的含义。后对41 名学生调查，全班无一人知道可以表示个，一致认为分数后面不可以加单位。这就说明量率不分问题的根源，关于分数量的含义未曾构建，学生在三年级形成的分数的概念是片面的。

五年级的《分数的意义》这部分内容由“分数的产生”和“分数的意义”两部分构成。关于“分数的产生”教材呈现两幅图，这两幅图揭示了分数产生的需要，这和三年级教材的呈现思路是一样的，但第二幅图是人教版教材第一次出现关于分数量的含义：每人分到（）块月饼、（）包饼干。按照教材的编排，在此之前学生是没有建构关于量的含义的分数概念，学生不可能靠着这一个情境就建立起分数的完整概念，并且紧接着教材编排的是“分数的意义”，重点在于单位1 的概念的形成，并没有编排量率区分这块内容。所以两个学段之间知识的断层会导致量率不分的问题在五年级暴露出来。

分数概念建构的不完整才是学生在量率不分的真正原因。所以教学中必须妥善处理好量与率的呈现方式，根据现有教材找到合适的教学策略。

三、分数的教学思考——形成概念体系

经过对三年级和五年级的教材梳理，笔者认为要避免知识间的断层就必须在三年级的《分数的初步认识》这个单元中构建完整的分数概念，分数量和率的含义必须都要建构。问题是怎样处理二者的关系呢？俞正强老师认为：关于量与率的混淆，在于对分数完全陌生时的同时呈现。解决之道是让学生先深刻经历关于量的分数认识，谂熟之后再经历关于分率的认识，在此基础上比较两个认识的差别，以解决量与分率的混淆问题。笔者认为俞老师的见解一针见血，再一次进行教学实践。

具体实施过程如下：

第一节课通过三个环节认识作为量的分数。环节一：分一分尝试用数字表示分的结果，体会分数产生的必要性。环节二：梳理分的过程，用分数表示分的结果。环节三：讨论用分数表示饼的大小的规律。本节课中分数一直作为量的表示而存在，目的是让学生对分数的量的表示印象深刻而充分。本节课之后学生对分数量的概念有了清楚的认识，对用个表示半个，个表示小半个非常认同。

第二节课以“倍”作为认识基础分数关系的含义。环节一：认识表示两个量之间关系的分数。环节二：认识表示部分与总体之间关系的分数。环节三：练习。本节课结束之后进行了课后测试，笔者发现学生对两个物体之间存在倍数关系情况用分数表征的题正确率较高，但对用分数表示整体与部分之间的关系的题错误率较高。例如一个圆平均分成8 份，涂出其中的1 份学生会错误地用来表示。

第三节课采用俞老师的两大环节只对材料稍作调整，环节一：对的不同理解，明确分数既可以表示量也可以表示关系。环节二：区别分数表示量还是关系。

本节课后进行了课后测试，发现学生对分数的量与率的区别有了较清楚的认知。但笔者发现很多学生的困惑是：半个是个，为什么2 倍的关系变成了一个是另一个的。经过与专家讨论，重新审视这三节课，笔者发现第一节课基于分物而产生的表示量的分数的思路是对的，问题出在第二节课，对于表示关系的分数是基于“倍”的关系而产生的。这和第一课时的思路不相统一，相当于另起炉灶，重新认识一个分数的含义，没有了像分物时产生分数的必要性，缺乏了二者之间的贯通性。加之本节是以两种物品之间的倍数关系引入，在无形中学生会先入为主地认为分数可以表征对这样的两物之间倍数关系，从而弱化整体与部分的思想，反而起到了负迁移的作用。

面对上述问题笔者思考：在构建分数概念时就必须构建完整的分数概念，量和率的含义必须都呈现。原因有三，其一，时间有限，不能够像认识整数那样先量后率。其二，学生的认识规律不同，认识整数时处在具体形象思维阶段，而分数的认识这个阶段的学生已经有了抽象逻辑思维能力。最后，已有经验不同，三年级的学生已经有了整数表征量与关系的知识储备，并且生活中也积累了一些与分数有关的常识。综合以上三个因素笔者认为分数的认识可以缩短周期，采取一种新的尝试：

策略一：双线并行，构建完整概念

分数的概念形成应该贯穿于《分数的初步认识》这个单元的始终，没有哪一个数学概念是可以通过一节完成的，笔者认为整个单元都应该量率并行构建完整的概念体系。分数产生是用于记录不完整实物的大小，那么分数的大小也应该是由记录实物的大小支撑。因此，需要对教材进行适当的调整，需要把教材中分数的简单应用例题1 提前至紧随几分之一之后，目的是希望通过几分之一的内容帮助学生建立分数两种含义的表象，再通过分数简单应用的例题1 实现单位1由1 个物品向多个物品转化，实现分数的两种含义的对比，进而辨清量与率的区别。《分数初步认识》教学设计如下：

环节一：分数的产生

分一分

（1）4 块月饼，分给两位同学？每人分到多少？怎么分？如果是2 块月饼呢？

（2）1 块呢？预设：把一块月饼平均分成2 半，每人分到半块。

此环节通过学生熟悉的生活场景，让学生体会分数产生的必要性。

环节二：探究分数的意义

任务一：理解分数表示量的意义

任务一是认识分数量的含义。设计是基于学生的思维方式进行，而学生通过操作活动可以更加直观地认识分数。

任务二：理解分数表示关系的含义

小结：像这样把一样东西平均分成两份，取其中的一份，都可以用来表示，在数学中，“半块”“0.5”“块”“张”“个”都可以说是原来的。

任务二：帮助学生通过对比观察概括引申出分数的另一种含义，对关系的表示，也就是人们常说的“率”。学生在分物的情境中进行直观的抽象概括，学生对表示部分与总体之间关系的分数的认识就比较深刻，也显得更加水到渠成，让学生在接触分数之时就明白分数有两种不同的含义。

环节三：认识几分之一、比较大小

创造四分之一，怎么得到的？为什么形状不同都可以用四分之一表示？

创造几分之一，这块月饼还可以怎样分？

比较大小。

几分之一的大小比较可以借助实物和面积模型直观进行比较，在这节课结束之后学生已经对分数的两种含义有了较全面的认识，没有出现分数无单位问题，对整体与部分关系表述也很清晰。并设计如下练习题进行巩固。

策略二：及时对比，辨清量与率

在分数的初步认识这节课之后学生对分数的两种含义的概念有了初步的感知，这就需要及时深入理解分数。接下来是“分数的简单应用”的第一个例题的教学。但学生还没学几分之几的内容，所以教师需要对教材的内容进行改编，改编后本节课例题用同一个情境分苹果。改编一：把第一题改成1 个苹果平均分成3 份，取一份。第一小题通过回顾再次明确块苹果是苹果的。改编二：第2 题改成6 个苹果平均分成2份、3 份，6 份取其中一份。在平均分的过程中知道1份苹果是总数的，是3 个，1 份苹果是总数的，是2 个……这样设计是将两个例题进行对比，突出量与率的区别，加深对分数两种含义的理解，也顺利实现了单位“1”由一个物体自然过渡到一些物体，并设计针对性习题：

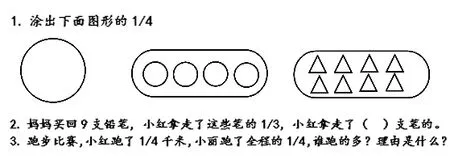
策略三：日常渗透，延长认识周期

分数概念的建构集中在三年级上册完成，教材编排上有4 个学期的空白期，所以教师在教学实践过程中必须进行日常的渗透，及时巩固复习。首先，在三年级下册到五年级上册这四个学期中教师要有意识地为学生创造运用分数知识的机会，可以把日常的解决问题的数值改编成分数呈现的形式。其次，要思考五年级下册“分数的意义”如何进行才可以和三年级知识巧妙衔接以形成完整的分数概念体系。在实际访谈中很多教师表示“分数的产生”三年级已经学过，只是量的含义没有接触，所以多数教师采取自学和简单讲解结合的形式处理。这显然不能有效地勾起学生关于分数的记忆，笔者认为这块内容需添加分数关系的内容，激发学生回忆起原有知识经验的基础上再进行分数单位的教学。

四、结语

分数是一个重要的数学概念，分数的学习丰富了数的概念，是小学数学教学中的一个难点。通过对教材的研究和多次的教学尝试发现分数概念的认识应该双线并行贯穿始终构建完整的概念体系，只有这样才能解决学生概念混淆的问题。当然文中所述教法未必是最合适的，还需要教师们在教学实践中不断探究思考。