基于多稳态柔性机构跨尺度微夹钳研究
2022-03-10关苗GUANMiao
关苗GUAN Miao
(西安工业大学机电工程学院,西安 710021)
0 引言
随着微电子技术和微纳米技术的快速发展,微机电系统(MEMS)、微装配和生物医学等领域成为了国内外研究的热点[1]。微夹钳(Microgripper)作为微装配系统的末端执行器,直接连接操作机构与微型零件,对微型零件的制造及装配起着决定性作用[2]。
微夹钳的主要功能是实现对微小零件和微型构件的抓取或夹持,对于需要操作的微小器件,其尺寸在微米、毫米级不等,用于微夹钳驱动器的位移分辨率高但驱动位移小,因此往往将驱动器输出的微小位移采用柔顺机构放大再传递给钳口[3]。相比传统的机械放大机构,双稳态及多稳态柔顺机构具有结构简单、易于制作、精度高、运动过程中摩擦磨损小等优点[4]。因此,本文基于多稳态柔性机构设计微夹钳。
对于扩大微夹钳的夹持行程,国内外学者进行了大量的研究,目前主要是通过柔顺位移放大机构实现。常用的微位移放大机构主要有杠杆放大机构、桥式放大机构、斯科特放大机构。李佳杰[5]等设计了一种新型二级差动式杠杆微位移放大机构,经过优化设计后机构的位移放大倍数为48,但有限元仿真模型与理论模型的误差为8%;Zhao[6]等设计了一种压电驱动的三级放大式微夹持器,放大倍数为16.8 倍,输出行程仅为102.3μm;丁严[7]等设计了一种两级放大的新型柔性微夹钳结构,位移放大比为30.89,单个夹爪的行程仅为334.01μm;陈晓东[8]等设计了一种大行程两级位移放大柔性压电微夹钳,无夹持物时,单边输出位移为237.82μm,实际放大倍数为23.782 倍。但是,以上的微夹钳不能同时夹持微米和毫米级别的物体。因此,研究出具有通用性好、适合跨尺度微操作等特性的微夹钳十分必要。
1 微夹钳结构设计
图1 为微夹钳结构图,整体尺寸为6.04mm×4.58mm×0.1mm。微夹钳由压电作动器、位移放大机构、柔顺多稳态结构、钳口和基座组成,左侧为放大机构,包含杠杆机构和平行四边形机构。右侧为柔顺多稳态机构,包含三个双稳态机构。钳臂通过平行四边形机构直接连接到固定基座上,隔绝寄生偏转运动,保证微夹钳末端输出为纯平行运动。
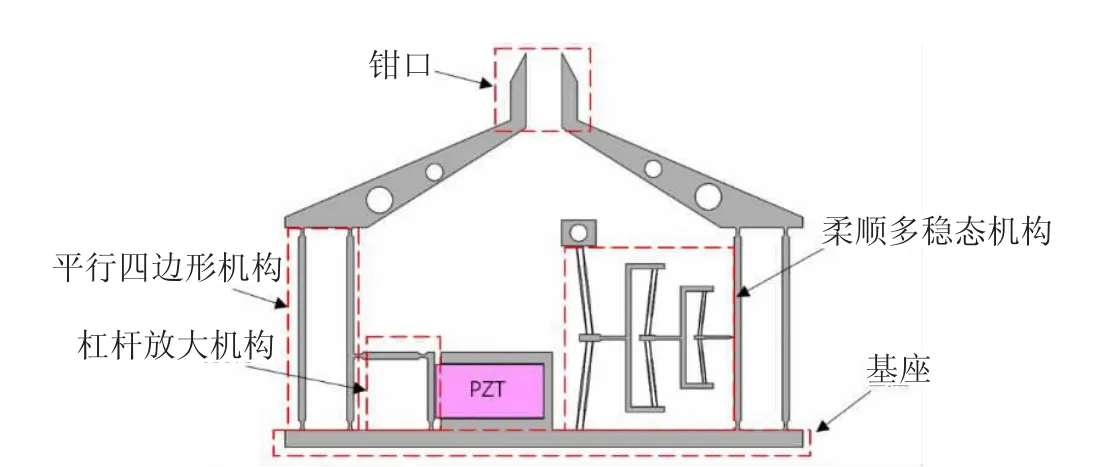
图1 微夹钳结构图
该微夹钳的工作原理为:微夹钳钳口为常开状态,输入端采用叠堆型压电陶瓷(PZT)作为作动器。通过压电作动器的伸缩运动实现夹持和释放动作。对压电作动器施加电压时,在微夹钳输入端会产生驱动位移,PZT 的一端固定,另一端与杠杆机构相连,压电作动器的输入位移先通过杠杆机构实现第一级放大,再将其传递给平行四边形机构保证钳口平动及第二级放大,右侧使用三个柔性双稳态机构串联实现八稳态,最后将位移传递至平行四边形机构实现钳口平动及放大。
2 微夹钳放大机构
2.1 放大机构结构设计
放大机构的简化示意图如图3 所示。在点A 处输入压电作动器产生的驱动位移Pin,经杠杆放大机构实现第一级放大,再通过平行四边形机构的传递实现第二级放大并保证微夹钳末端为纯平行移动,最终在F 点处得到整个放大机构的输出位移Xout。l1为杠杆放大机构输入端到固定端B 的距离,l2为第一级杠杆机构的输出端C 到固定端B 的距离,l3和l4分别为第二级杠杆的输入端D 和输出端F 到固定端E 的距离,第一级杠杆和第二级平行四边形机构分别以柔性铰链H1和H3的中心轴为转动轴进行转动。上述各参数设定为:l1=394.5μm,l2=789μm,l3=710μm,l4=1339μm。
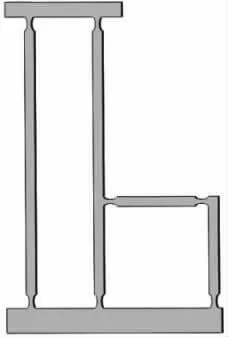
图2 杠杆结构图
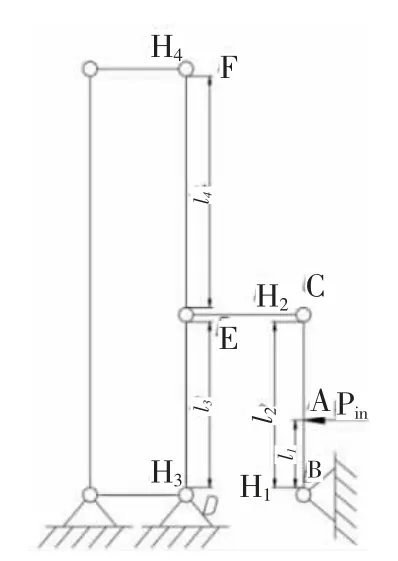
图3 杠杆结构简化示意图
2.2 放大机构放大倍数确定
该放大机构的运动过程中,在力的作用下,柔性铰链会同时产生拉伸、压缩以及转角变形,从而导致柔性铰链的旋转中心发生漂移,使得杠杆放大机构以及整个微夹钳的放大系数发生改变。因此在进行杠杆放大机构理论的研究中,需要考虑柔性铰链旋转中心漂移对放大系数的影响。设作用在柔性铰链Hi处的轴向力为Fi,力矩为Mi,柔性铰链Hi绕其中心轴的转动角为θi,轴向变形量为Δi,杠杆放大机构中第一级杠杆ABC 的转角为φ1,第一级杠杆ABC 和第二级杠杆DEF 间的过度杆CE 的转角为φ2,第二级杠杆DEF 的转角为φ3。
杠杆机构的输入位移即为压电作动器的输出位移Pin,即:

BC 杆的受力示意图如图4所示,可得:
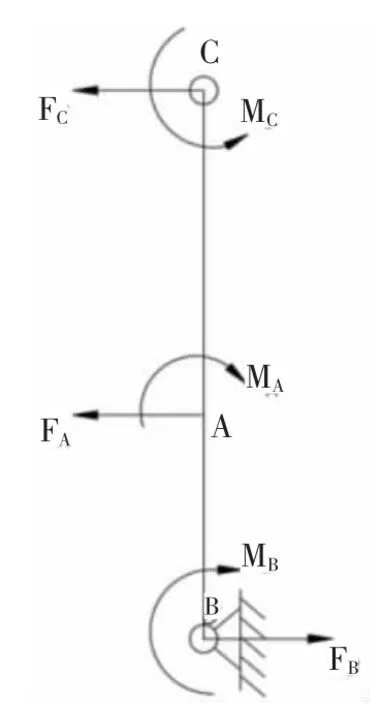
图4 BC 杆的受力示意图
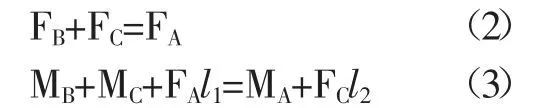
铰链B 受轴向力作用会产生压缩,压缩位移为ΔB,因此在通过柔性铰链B 后的有效输出位移为:
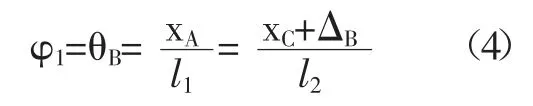
综上可得第一级杠杆输出位移为:

一、二级杠杆中间的杆CE 受力示意图如图5 所示,根据其变形情况可得:


图5 杆CE 受力示意图
铰链H2受轴向力作用产生压缩,压缩位移为ΔC,因此在通过柔性铰链H2后第一级杠杆的有效输出位移为:

平行四边形机构的受力示意图如图6 所示,根据其受力分析可得:
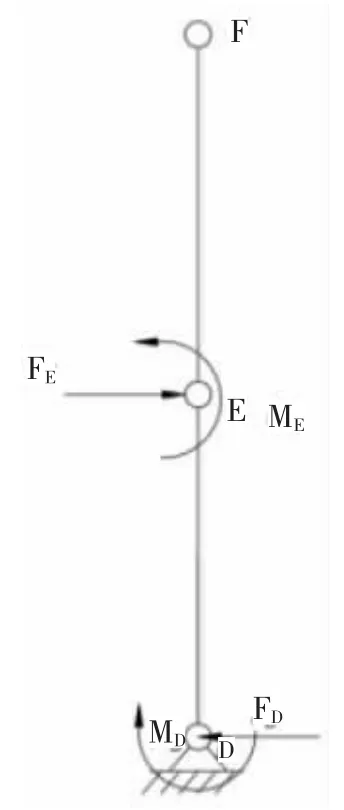
图6 杆DEF 受力示意图

平行四边形机构的输入端为点E,铰链H3受轴向力会产生压缩,压缩量为Δ3;同时铰链H3绕旋转中心转动,转动角为φ3,则有:
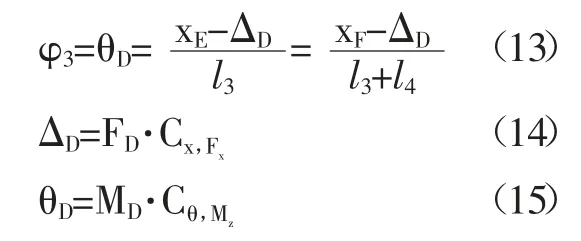
综上整个放大机构的有效输出位移为:
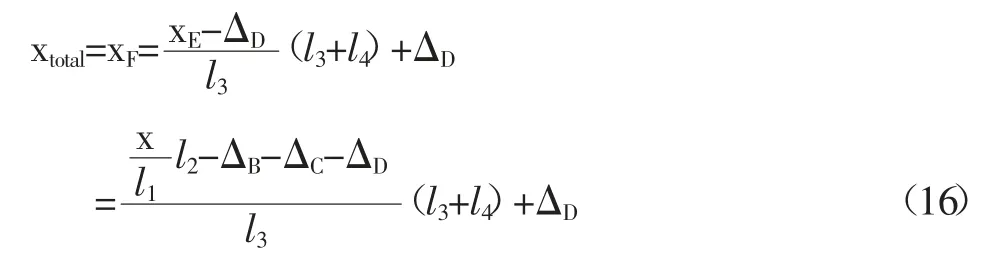
整个放大机构的放大倍数为:
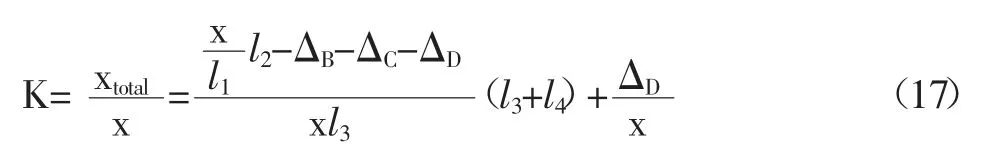
代入具体数据,K=4.52。
2.3 放大机构仿真分析
根据上述推导的放大机构的放大倍数,接下来使用有限元分析对这些公式进行验证。根据图2 所示的几何模型建立有限元仿真模型,分析该放大机构的运动范围和应力情况。在放大机构输入端施加120μm 的位移,结果如图7所示,最大输出位移为499.78μm。

图7 放大机构位移图
通过有限元仿真得出左侧放大机构的放大倍数为4.16,而理论模型计算得出放大倍率为4.52,与有限元仿真结果相比误差为8.6%。
3 多稳态结构设计及仿真分析
3.1 单个双稳态理论分析
为了深入了解不同参数对双稳态稳定特性的影响,并选择最适合控制多稳态性能的设计参数,首先分析单个柔顺双稳态模型,如图8 所示。该双稳态初始状态为弯曲状态、长度为L、矩形截面面积为A=b×d 和二阶矩Iyy=bd3/12。双稳态的初始状态可以用函数Z0(x)=hψ(x)来表示,其中h 是双稳态的中心点到初始位置的高度,ψ(x)是一个无量纲的函数。
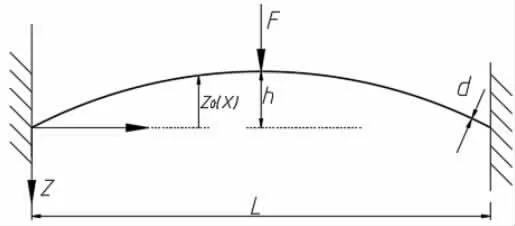
图8 单个柔顺双稳态模型
经分析,得到:
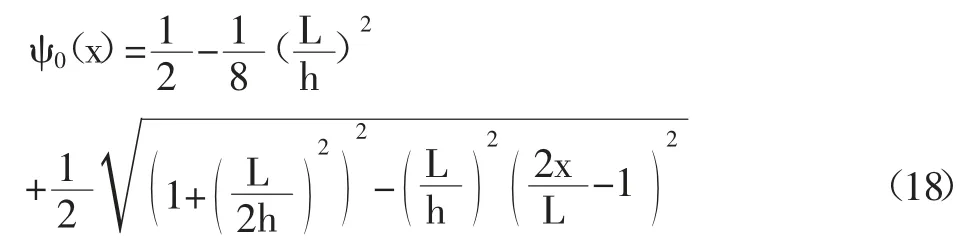
双稳态初始加工状态为弯曲形状,因此梁在其初始弯曲状态是无应力的。假设梁是由杨氏模量为E 的各向均匀线弹性材料制成,将两端固定,在z 方向上由作用于梁中点的集中力F 驱动,如图8 所示。
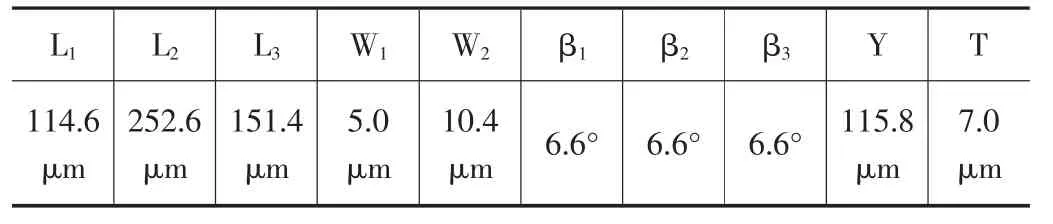
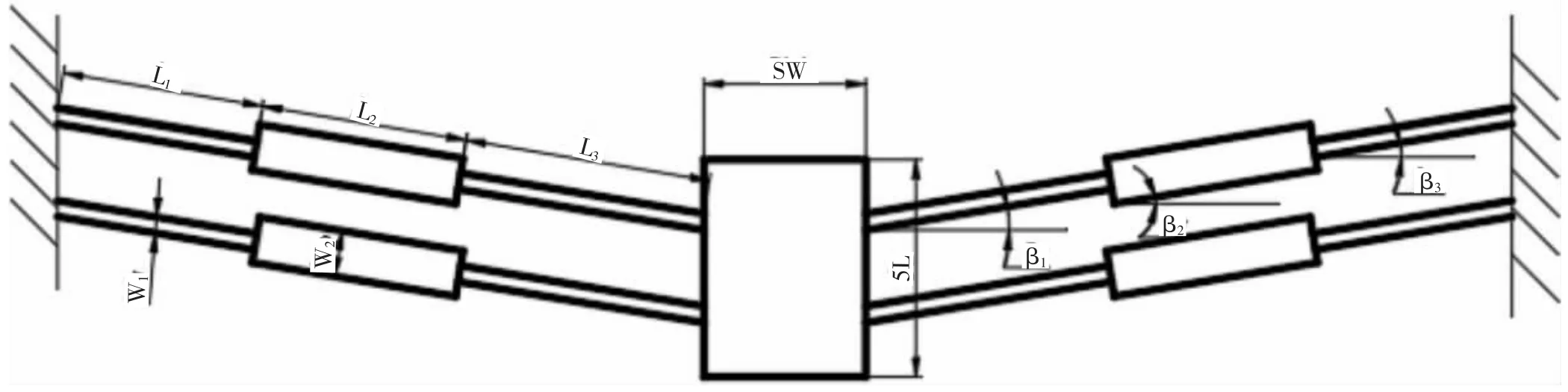
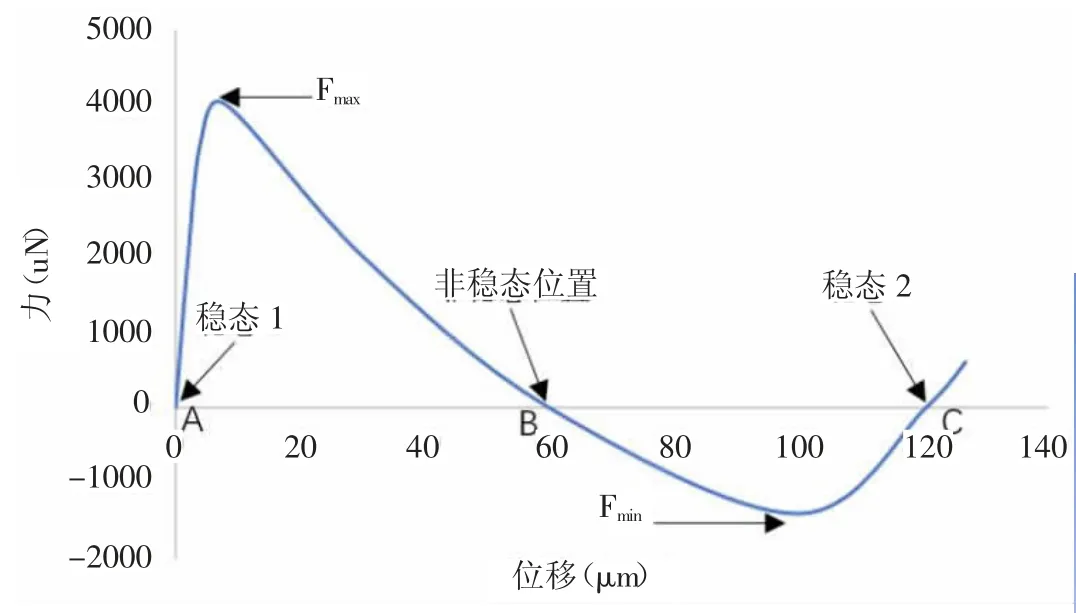
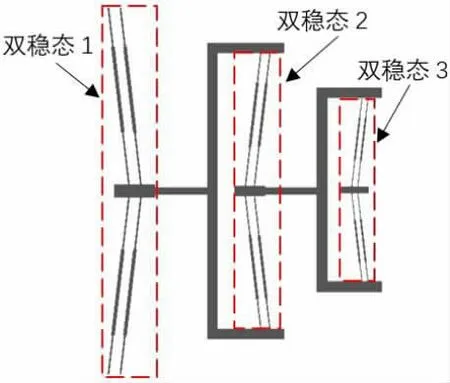
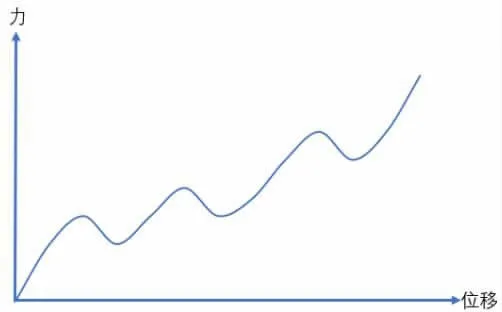
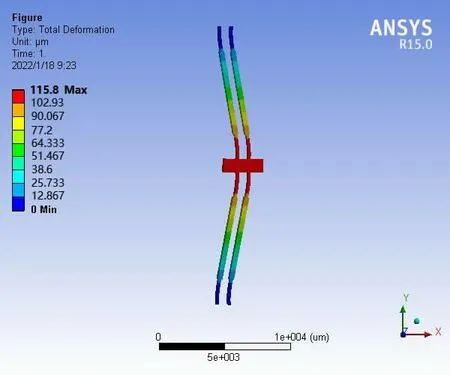
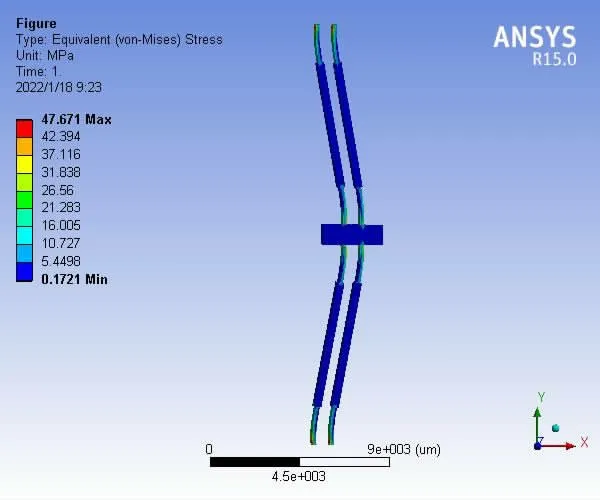
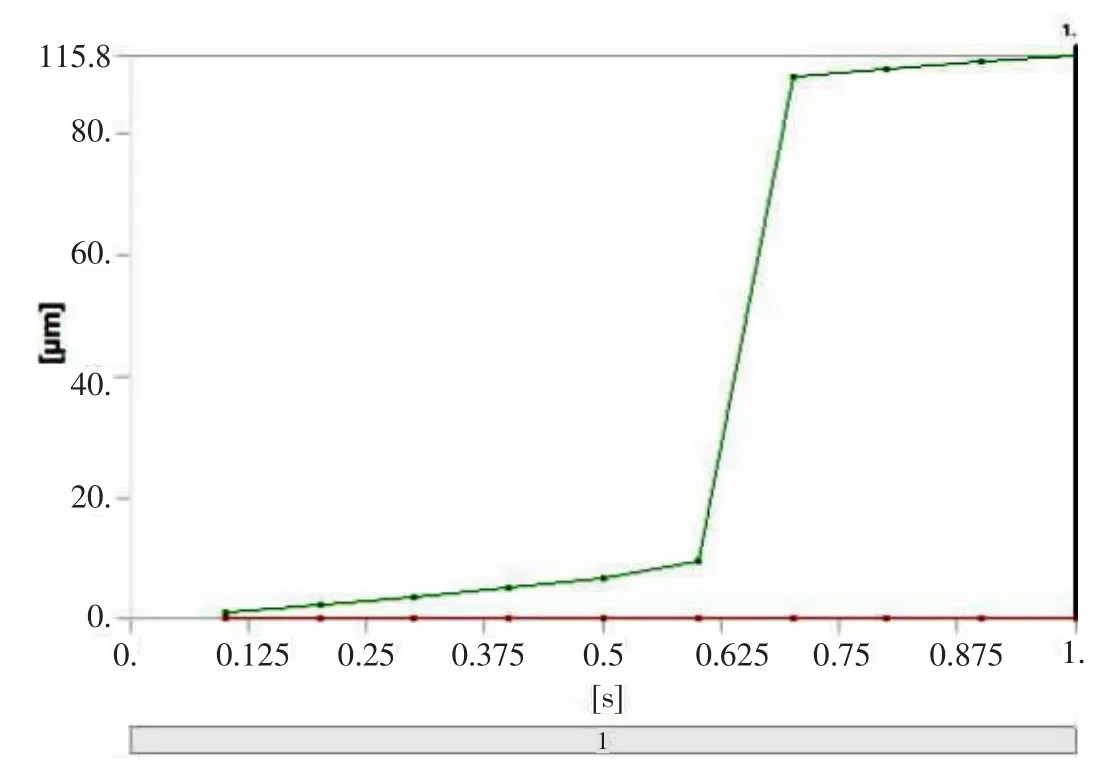
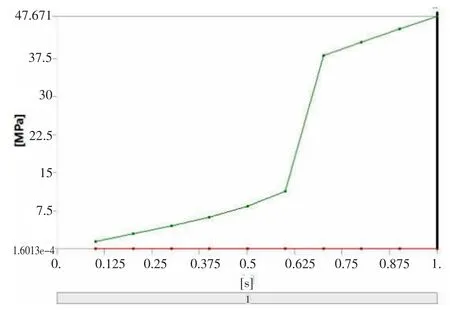
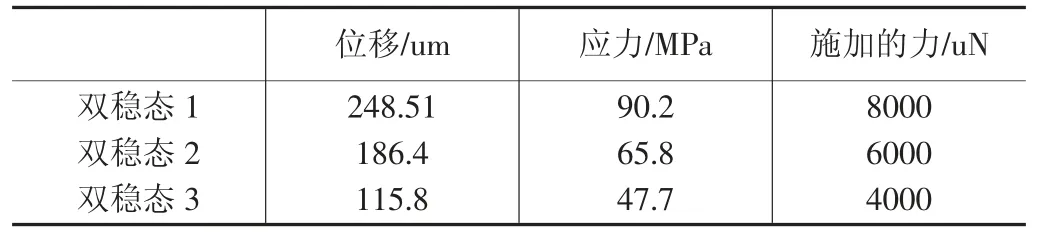
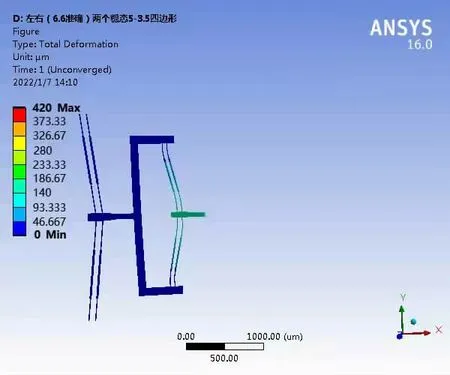
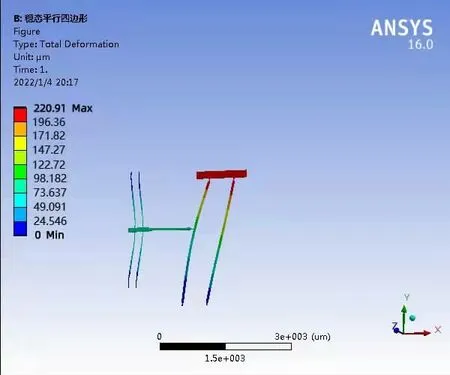
首先采用欧拉伯努利理论建立梁的理论模型,便于对双稳态的初步设计参数进行调整。此外,该模型的理论结果将用于与有限元结果的比较。假设d< 其中w(x)为横向位移;u(x)是轴向位移,δ(x)是狄拉克函数。式(19)由梁两端固定的边界条件推导得到。两个相同的梁通过刚性连接组成双稳态结构,因此它是对称的,在梁的中点处有边界条件w′=0,EIyyW′′′=F/2。对式(20)的方程组进行了数值求解,该解基于配点法[9],利用集成到Matlab 包中的两点边值问题求解器bvp4c[10]得到。方程组(20)写成六个一阶微分方程的形式: 根据上述理论可得出双稳态跳转位移即上式中的横向位移w(x)与结构参数之间的关系,由此设计了双稳态的结构,参数如表1 所示,图9 显示了参数化设计的重要变量,其中L 表示刚性杆长、W 表示刚性杆宽度,β 表示杆的角度,T 表示厚度,SW、SL 分别表示梭子的宽度和长度,Y 表示驱动梭的位移,材料选择为铝合金,其杨氏模量(EX)为71GPa、泊松比(PR)是0.33。双稳态机构依靠柔顺杆的偏转移动到它的交替稳定位置。 表1 三段式柔顺双稳态机构设计参数值 图9 双稳态机构的结构示意图 该双稳态机构具有两个明显的稳定平衡位置,图10是用非线性有限元分析得到的柔顺双稳态机构力-位移关系曲线。力-位移特性曲线上的A 点和C 点分别为两个稳态位置(A 点代表初始位置),B 点是非稳态位置。Fmax是该双稳态从第一个稳态位置跳转到第二个稳态位置所施加的力,而Fmin是其从第二个稳态位置跳转到第一个稳态位置所施加的力。A 点和C 点之间是双稳态特性段,在此区间内柔顺双稳态机构由初始位置A 经非稳态位置B 点跳转至第二稳态位置C 点。 图10 柔顺双稳态机构力-位移曲线 将多个柔顺双稳态机构串联以实现多稳态功能,每个双稳态连接一个刚性框架,如图11 所示。将双稳态由左至右分别命名为双稳态1、双稳态2 和双稳态3。其中每个双稳态所需的跳转力应不同,因此在施加的力不断增加的情况下会发生一系列的稳态突变,如图12 所示。 图11 多稳态结构 图12 多稳态突变曲线 下面通过有限元仿真来验证上述多稳态理论模型。由于这三个双稳态结构相似,所以只仿真其中的一个双稳态3。本文选用铝合金材料(其屈服强度与杨氏模量的比值较高,对柔顺机构而言,在材料性能允许的情况下,可获得更大的工作空间),其弹性模量E=71GPa,泊松比PR=0.33,切屈服强度σ=275MPa,密度ρ=2770kg/m3。 有限元仿真结果如图13、图14 所示。由图可看出双稳态3 的跨度为115.8um,应力为47.7MPa,未超出材料的最大许用应力275MPa。 图13 双稳态位移图 图14 双稳态应力图 由图15、图16 可看出双稳态位移和应力都有突变,可知双稳态3 确实实现了跳转。所有双稳态的仿真数据如表2 所示。 图15 双稳态位移曲线 图16 双稳态应力曲线 表2 双稳态仿真数据 接下来将双稳态1 和2 串联进行仿真,结果如图17所示,位移约等于两个双稳态单独位移之和。 图17 两个双稳态串联位移图 将双稳态3 和平行四边形串联进行仿真,结果如图18 所示,经过平行四边形后,位移放大了2 倍左右,与理论值基本吻合。 图18 双稳态和平行四边形机构串联位移图 最终多个双稳态加平行四边形结构的总位移为1025.91um,可实现微米到毫米跨尺度的要求。最大应力为200.91MPa,小于铝合金的最大许用应力275MPa,所以,设计的多稳态结构满足微夹钳要求。 本文设计了一种基于多稳态柔顺机构跨尺度微夹钳,该机构具有结构紧凑、位移范围大、平动夹持的优点,可实现微米到毫米级别跨尺度微操作。运用静力学模型,对微夹钳的结构进行了理论分析与设计,并利用有限元仿真分析软件验证了微夹钳的性能。与同类微夹钳相比,该微夹钳具有良好的实用价值。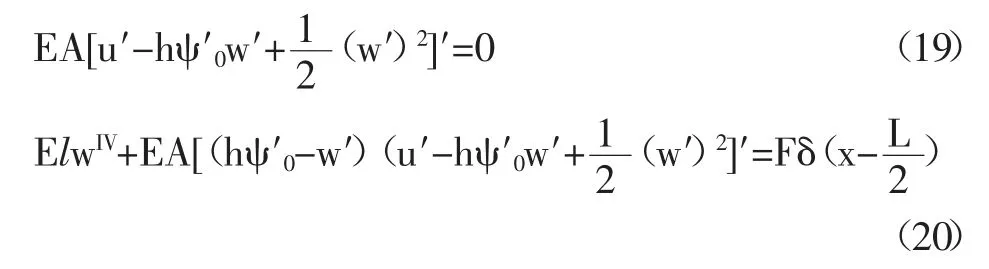

3.2 多稳态结构设计
3.3 多稳态仿真分析
4 结论
