后量子密码CRYSTALS-Kyber的FPGA多路并行优化实现
2022-03-10李斌陈晓杰冯峰周清雷
李斌,陈晓杰,冯峰,周清雷
(1.郑州大学计算机与人工智能学院,河南 郑州 450001;2.信息工程大学数学工程与先进计算国家重点实验室,河南 郑州 450001)
0 引言
随着量子计算的发展,传统公钥密码体制面临着严重的安全问题。基于格困难的密码算法具有加密效率高和抗量子攻击等优势,成为研究热点。美国国家标准与技术研究院(NIST,National Institute of Standards and Technology)从2016 年起征集了后量子密码的标准化评选,提出了众多基于格的后量子密码方案[1]。在各种密码方案中,公钥加密体制是非常重要的一个分支,主要被应用于密钥的分配和数字签名。NIST 最近公布了第三轮4 个基于格的公钥加密算法,CRYSTALS-Kyber 便是其中之一。
在Kyber 格密码方案中[2],多项式乘法运算是关键步骤,消耗了绝大部分时间和资源。现有方案中,基于蝶形运算的数论变换[3](NTT,number theoretic transform)可以快速实现多项式的乘法。但是,在NTT 计算过程中,蝶形运算会被执行多次,且包含模加减、模乘、模约简等多种运算[4],极大影响了硬件整体计算效率。其次,NTT 控制逻辑包含多次循环嵌套的运算,计算结构复杂。最后,多项式系数的存取和调度复杂,且对通信带宽具有较高的要求。因此,如何利用可重构硬件现场可编程门阵列(FPGA,field programmable gate array)实现高效的NTT多项式乘法,这一问题亟待解决。
当前,对于格密码系统的实现,仍需要兼顾硬件的执行效率和资源消耗,需要尽量多的并行结构,以实现更快的运算速度。由此,围绕后量子密码高效能的应用需求,本文开展了Kyber 算法的优化设计研究。首先,对Kyber 算法进行了描述,分析了NTT、逆向数论变换(INTT,inverse NTT)及系数对位相乘(CWM,coefficient-wise multiplication)等算法流程。然后,详细给出了流水线蝶形运算单元的优化设计,并以多通道RAM 优化访存,减少计算时延。最后,以32 个蝶形运算单元并行运算,实现了FPGA 整体架构,提高了计算效率。
1 相关工作
1.1 Kyber 算法简介
整数环用Z 表示,Zq表示整数环模q的商环,Rq=Zq[x]/ϕ(x)表示模多项式ϕ(x)的整系数多项式环,其中ϕ(x)为不可约简多项式。大部分情况下ϕ(x)=xn+1,则Rq=Zq[x]/(xn+1)表示次数最多为n-1的多项式环。
NTT 是在离散傅里叶变换(DFT,discrete Fourier transform)数论基础上实现的,是定义在环Zq上的线性正交变换,只在整数环上进行运算。对于多项式,有

在Kyber 算法中,NTT、INTT 和CWM 算法流程如算法1、算法2 和算法3 所示,其中brl-1(k)和brl-1(i)分别表示对k和i进行l-1 位的比特逆序操作。
算法1NTT 算法

算法2INTT 算法
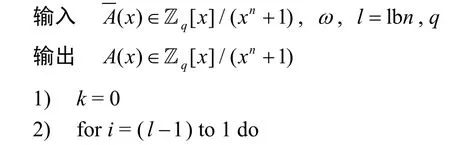
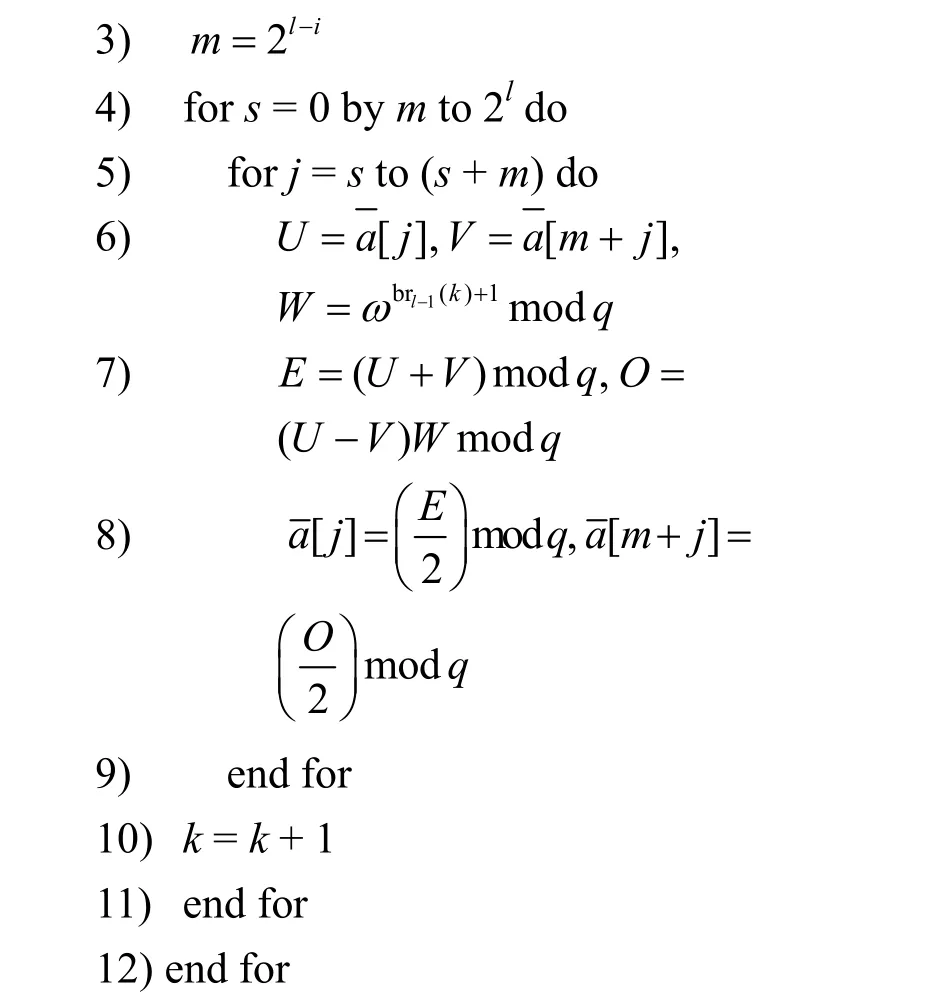
算法3CWM 算法

此外,在Kyber 算法中,对NTT/INTT 操作进行了优化处理,将原有的256 次多项式拆分为2 个128 次多项式,并以2 个128 次多项式独立进行计算。因此,在CWM 算法中,需要进行128 次二次多项式的乘法运算。
Kyber 算法的参数如表1 所示,其中k用于选择多项式矩阵的维度,并调整算法安全等级。
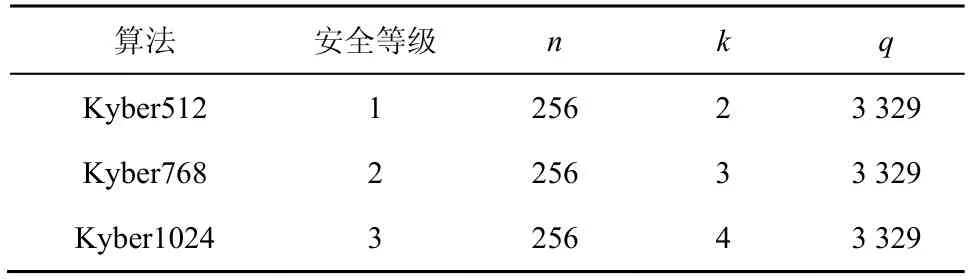
表1 Kyber 算法参数
Kyber 算法的密钥生成、加密和解密过程如下。


从Kyber 算法流程中可以看出,密钥生成过程需要2k次NTT 和k2次CWM 运算;加密过程需要k次NTT、k+k2次CWM 和k+1 次INTT 运算;解密过程需要k次NTT、k次CWM 和一次INTT运算。
1.2 硬件相关实现
目前,对于Kyber 算法的研究主要集中在对NTT 算法的优化加速,包括蝶形运算、存储访问和指令集的优化。
为此,Yaman 等[5]以16 个蝶形运算单元加速了NTT/INTT的计算,但是其模约简计算较复杂,仍有优化空间。Huang 等[6]在Xilinx Artix-7 和Virtex-7 FPGA 上对Kyber 算法进行了优化实现,并以流水线形式实现了NTT 模块,但其NTT 计算周期较长。Mert 等[7]以蒙哥马利模乘设计了蝶形运算单元,并可通过参数进行配置,以多运算单元(PE,processing element)并行完成NTT的计算。此外,Mert 等[8]又采用蒙哥马利模乘,以字为单位对NTT进行了优化,并通过PCIe 以直接存储器访问(DMA,direct memory access)方式完成了软硬件协同实现。Xing 等[9]在Xilinx Artix-7 上实现了完整的Kyber 算法,包括SHA3 和NTT/INTT的计算,但程序仍以串行执行为主,NTT的计算需要512 个时钟周期。Ricci 等[10]在Xilinx Virtex UltraScale+XCVU7P 高性能FPGA 上实现了Kyber的NTT 运算,频率达到了637 MHz,但其计算周期仍高达405 个时钟周期。同时,Ricci 等[11]又在该FPGA 上实现了CRYSTALS-Dilithium 数字签名算法,以4 个蝶形运算单元每次输入2 组数据加速了计算。Chen 等[12]采用双列顺序存储来解决RAM 读写冲突的问题,并以流水线技术优化了蝶形运算。Seiler 等[13]以AVX2 指令集优化了NTT 算法,并在Skylake 处理器上实现了6.3 倍的性能提升。Zijlstra 等[14]以高层次综合(HLS,high-level synthesis)对Kyber 算法进行优化实现,并对各种实现在资源和时间消耗方面进行了详细对比。Basu 等[15]以HLS 对多个后量子公钥加密算法和数字签名算法进行了实现,并在资源和性能间进行了对比分析。Agrawal 等[16]实现了寄存器传输级(RTL, register transfer level)代码库以硬件原语的方式提供n个点的NTT 运算。Bisheh-Nias ar 等[17]采用K2-RED模约简算法对NTT和INTT 进行了优化,减少了资源占用,并提高了计算频率。但K2-RED 算法需要额外对ω进行预计算,且不支持CWM的运算。Fritzmann等[18]在FPGA上设计了RISQ-V 指令集,加速了Kyber 算法的计算。
在国内,陈朝晖等[19]采用乒乓结构存储多项式系数,并以可选层级的流水线结构,减少了蝶形运算单元的逻辑资源占用。刘冬生等[20]在Xilinx Artix-7 上设计了一种基于RAM的可重构多通道数论变换单元,支持不同参数的可重构配置。华斯亮等[21]设计实现了基32的数论变换硬件结构,以操作数合并和快速取模,提高了蝶形运算的计算效率。沈诗羽等[22]给出了一种针对我国Aigis 后量子密码算法的高效AVX2 和ARM 优化方案,提升了算法整体性能。
综上可以看出,想要提高Kyber 算法的FPGA实现速度,一是要对关键路径进行分解,深度优化,提高计算效率;二是要增加并行度,包括各模块间的并行和同时处理数据的能力。虽然上述方案在一定程度上加速了Kyber 算法的计算,但大部分方案的NTT 计算周期长,并行程度不高,仍无法满足高性能计算的需求。同时,部分方案仅实现了NTT和INTT 运算,并不支持CWM 运算。为此,本文从Kyber的NTT、INTT 和CWM 各计算阶段着手分析,针对不同的运算、存储和通信特征选择合适的实现方式,提高计算效率。
2 算法优化设计
2.1 整体结构
为提高Kyber 算法硬件实现整体灵活性和可扩展性,在FPGA 内放置32 个蝶形运算单元,各个蝶形运算单元可独立执行。其次,放置多RAM通道对多项式系数和每次迭代的结果进行存取。对于参数ω,采用预计算的方式提前计算好,并以ROM的形式进行存储。最后,由控制逻辑完成对蝶形运算单元的输入输出的控制、RAM 存取地址的控制及参数ω的读取控制。FPGA 整体结构如图1 所示。

图1 FPGA 整体结构
从NTT、INTT 算法流程中可以看出,每次迭代读取和写入的参数是不同的。因此,需要通过仲裁对RAM 进行读写。同时,在CWM 算法中,需要多次计算模乘,因此在蝶形运算单元中以M输出中间模乘的结果,并再次送入蝶形运算单元进行最终结果的计算。可以看出,FPGA 整个架构以松耦合方式互连,并可根据参数配置,灵活完成NTT、INTT 和CWM 这3 种运算。
2.2 蝶形运算单元
蝶形运算单元是NTT、INTT 和CWM 计算的核心。这里,采用流水线的结构进行实现,并根据控制信号,选择NTT、INTT 和CWM 不同计算的流程。蝶形运算单元结构如图2 所示。
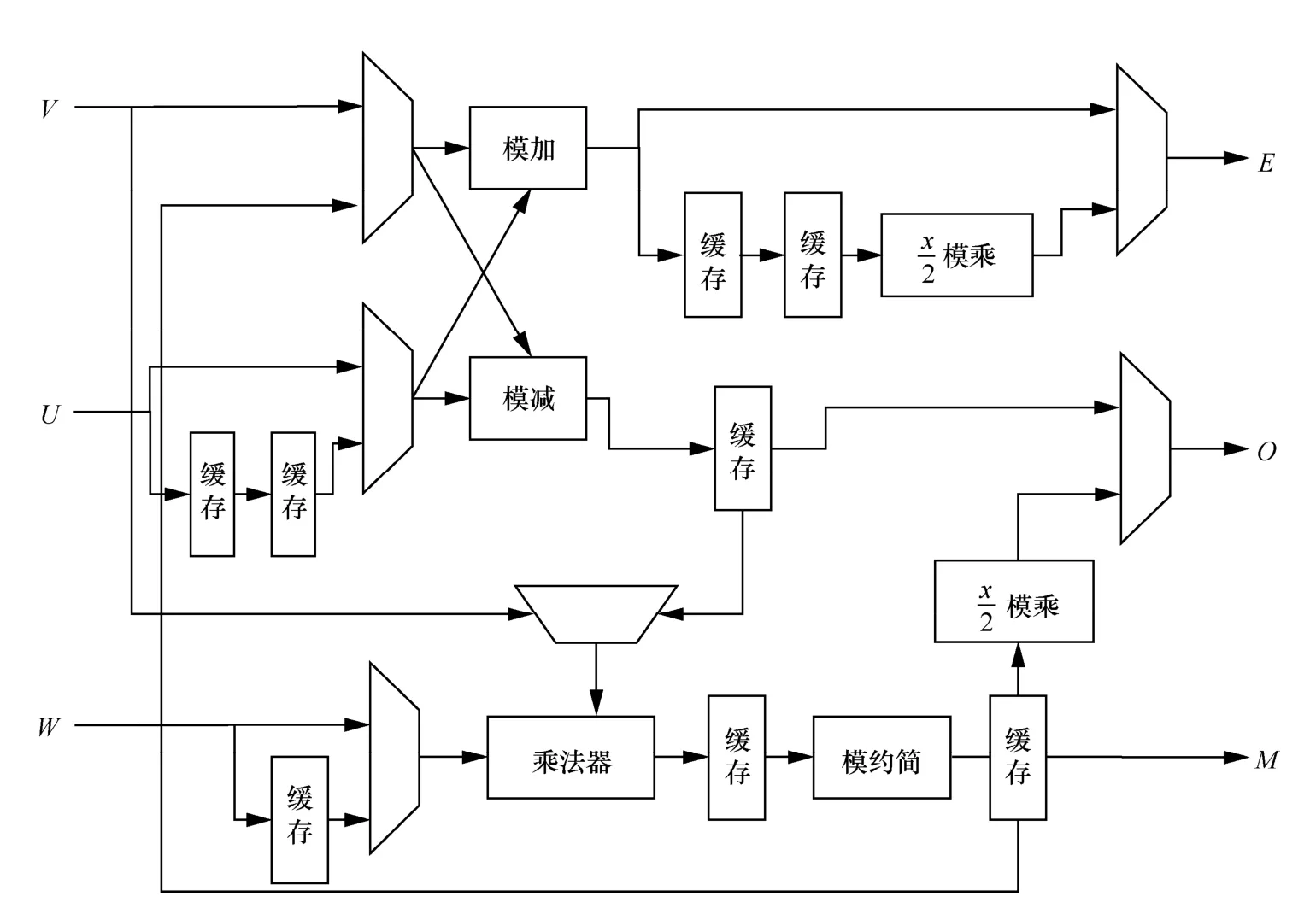
图2 蝶形运算单元
由于NTT 先计算模乘,再计算模加减,而INTT先计算模加减再计算模乘,两者计算的先后顺序不同。因此在蝶形运算单元中插入了多个缓存寄存器,用来缓存中间结果,并根据控制信号,进行仲裁输出。同时,通过缓存也降低了蝶形运算的逻辑层级,避免产生较大的路径时延。其次,NTT/INTT每次存取参数的RAM 不一致,且输出的E和O这2 个结果可能存入同一RAM 中,因此需要E和O按次序写入。具体地,在NTT/INTT 中,输出E需要3 个时钟周期,输出O需要4 个时钟周期,并按先E后O写入RAM。再次,对于CWM 算法,需要多次计算模乘和模加,由此需要对中间模乘结果M进行缓存,并以状态机控制传值完成后续计算。最后,使用DSP 实现乘法器,充分利用FPGA 芯片资源。蝶形运算单元流水线各阶段如图3 所示。

图3 流水线阶段示意
在蝶形运算单元中,模加减可由组合逻辑进行实现,并根据加减结果是否超出素数q(q=3 329)的范围,再进行处理判断,其结构如图4 和图5 所示。
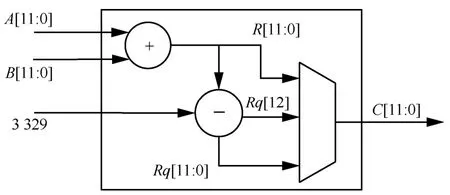
图4 模加硬件结构

图5 模减硬件结构
在图4 和图5 中,A和B为12 bit的输入,C为12 bit的输出,R和Rq为13 bit的中间计算结果,并根据R或Rq的最高位进行判断输出最终的模加减结果。而模约简和模乘需要根据Kyber 算法参数进行深度优化,以减少资源消耗并提高运算速度。具体地,本文通过Barrett 算法实现模约简,再以逻辑公式变换优化模乘,详细介绍如下。
2.2.1Barrett 模约简
Barrett 算法利用乘法和模约简运算代替了高成本的除法来实现取模运算,可计算任何参数的模乘。对于0 ≤x<q,0 ≤y<q,则xy<q2。为计算zm=xymodq,0 ≤ zm <q,令sp=xy,如果存在wa 使sp=qwa +zm,即可求得zm。

具体地,Barrett 模约简如算法4 所示。
算法4Barrett 模约简


对于结果dif,其取值范围为[-3q,2q),因此需要再根据dif 高2 位进行判断处理。最后,将zm 与q进行比较判断,并计算输出最终结果。
2.2.2模乘优化

2.2.3CWM 调度优化
对于CWM,需要在 Zq[x]/(x2-ω)上计算二次多项式乘法(a0+a1x)(b0+b1x)。在算法3 中,可以看到需要分别计算a0b1、a1b0、a1b1W和a0b0,共5 次模乘和2 次模加。对于模乘需要3 个时钟进行计算,而模加只要需要一个时钟周期。由此,在第1 个时钟周期先计算a1b0,并在第4 个时钟周期将a1b0缓存的结果与a0b1共同输入蝶形运算单元,在a0b1做完模乘运算后,直接完成a1b0+a0b1的模加运算。同理,先计算a1b1,再计算a0b0。如此,不仅减少了CWM 中间等待的过程,并可在8 个时钟周期内完成二次多项式乘法,还提高了CWM的计算效率。具体地,CWM 中二次多项式调用流程如图6 所示。

图6 CWM 中二次多项式乘法调用流程
2.3 多RAM 访存优化
对于N个点的NTT,共需要执行lbN轮蝶形运算,且每轮对RAM的访问需要唯一的地址来存取参数。8 个点的蝶形运算和RAM 访问如图7 所示,灰色节点表示蝶形运算。
从图7(a)中可以看出,在第1 阶段,4 组系数对(0,4)、(1,5)、(2,6)和(3,7)会分别进行蝶形运算。因此需要在一个时钟周期内,从RAM 中读取各组系数对。那么,可以采用2 个RAM(RAM0 和RAM1)分别存储第0、1、2、3 和4、5、6、7 个系数进行实现。此外,由于每个阶段的系数对都会发生变化。在第2 个阶段,参与蝶形运算的4 组系数对为(0,2)、(1,3)、(4,6)和(5,7)。因此需要将第1阶段(0,4)和(1,5)的输出结果存入RAM0 中,(2,6)和(3,7)的结果存入RAM1 中。如此,可以确保在第2 阶段,仍在一个时钟周期内从RAM0 和RAM1中读取到相应的系数对。同理,对于第3 阶段的计算,也需要调整第2 阶段RAM的存储。

图7 8 个点的蝶形运算和RAM 访问
对于Kyber 算法,多项式有256 个系数,由于将其拆分为2 个128 次多项式,则共需要执行7 轮蝶形运算,对RAM的存取更为复杂。以下给出Kyber 算法的访存优化方法。
2.3.1多RAM 存储
首先,本文方案共有32 个蝶形运算单元,则需要采用64 个RAM,每个RAM 对应有4 个地址,共有64×4=256 个参数。RAM 初始化参数存储如图8所示。

图8 RAM 初始化参数存储
图8 中,每2 个RAM 对应一个蝶形运算单元,且第2i个和第2i+1 个(0≤i< 32,i=i+2)RAM分别存取各自的系数对。如此,32 个蝶形运算单元可独立并行读取参数并执行。
其次,由于采用64 个RAM 对中间结果进行存取,需要确保RAM 地址的读写顺序,防止读写冲突。为此,对RAM 进行了扩容,将RAM 分为高低2 个地址段。以NTT 为例,在首轮参数存入RAM后,从地址0~3 开始读取数据,并将蝶形运算的结果写入地址4~7。而后再从地址4~7 读取数据,并将蝶形运算的结果写入地址0~3。如此循环,以低地址空间和高地址空间的交替迭代操作,实现了每轮参数的有序存取。RAM 存取模式如图9 所示。
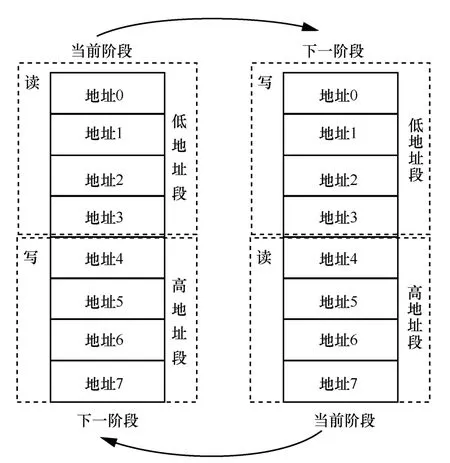
图9 RAM 存取模式
最后,对于ω的读取,由于每轮蝶形运算输入的参数不同,需要预处理后,按一定的规则进行存储。具体地,对于NTT,从地址0 到22;对于INTT,从地址23 到45;对于CWM,从地址46 到49,每个地址分别有32 个数据,存入ROM 中。以NTT 运算为例,其ROM 存储内容如图10 所示。
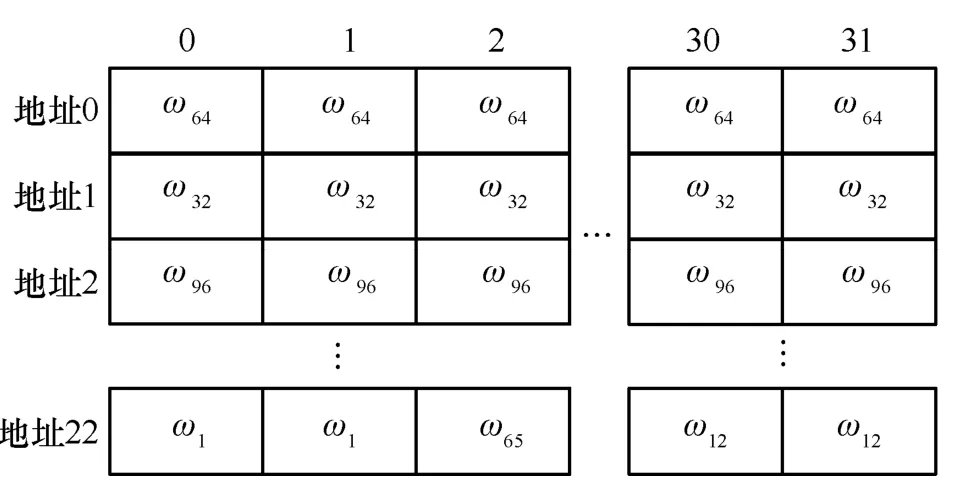
图10 NTT 中ω的ROM 存储
2.3.2数据存取控制
Kyber 每轮蝶形运算读写的参数不同,且地址唯一。在读取参数时,为方便操作,对参数进行重排,统一读取64 个RAM的某一地址,获取所有256 个参数并组成系数对。因此,在写入中间结果时,需要对输出的E和O分别按不同的地址进行存储,以保证在下一轮可以从同一个地址再次读取到对应的系数对。具体地,这里采用一个地址raddr对所有RAM 进行读取,2 个地址waddre 和waddro分别完成E和O的RAM 写入。
另外,由于RAM 空间被分为低地址空间和高地址空间,每轮交替使用高地址空间或低地址空间。因此需要对raddr、waddre 和waddro的高位进行交替翻转,低位则按照每轮读写的地址正常进行变化。以NTT 运算为例,具体的raddr、waddre 和waddro 计算如算法5 和算法6 所示。
算法5RAM 读地址的变换

在算法5的步骤1)中,当bau_stage 大于1 时,直接根据bau_loop 即可获取RAM的读地址。对于步骤2),则需要根据当前bau_stage 和bau_loop 进行额外的计算,从而获得RAM的读地址。最后,在步骤4)~步骤6),当raddr[1:0]由0 累加到3 时,raddr[2]会进行翻转,从而使raddr[2:0]由4到7进行地址累加。
算法6RAM 写地址的变换

同理,在算法6 中,当bau_stage 大于1 时,可直接根据bau_loop 获取RAM的写地址,而其他情况要根据当前bau_stage 和bau_loop 进行计算,从而获得RAM的写地址。最后,在步骤5)~步骤7),对waddre[2]和waddro[2]高位进行翻转。
由于RAM的读写需要先获取地址,然后才能读写数据,即RAM的操作需要一定的时间间隔。而蝶形运算是以流水线方式执行的,可连续对数据进行处理。因此需要处理好流水线和RAM 访问之间的关系,防止数据中断出错。
如图11 所示,将数据送入流水线时,预先计算出RAM 读写地址,并对地址进行打拍缓存。具体地,在蝶形运算的前2 轮,中间需要等待2~3 个时钟周期。这是由于前2 轮,地址不是按序读写的,需要额外的等待。在第3~7 轮,中间只需要等待一个时钟周期,即在当前RAM 地址写入后,下一个时钟可立即读取。

图11 RAM 读写等待示意
2.3.3RAM 资源复用
Kyber 算法中需要输入2 个多项式A(x)和B(x),为此通过2 组RAM 分别存储,如图12 所示。这样可一次将A(x)和B(x)的所需参数写入RAM。然后在CWM 计算过程中,可直接从2 组RAM 中读取数据,并将多项式乘法结果再次存入其中一组RAM 中。随后,再由控制信号完成INNT运算,并写入其中一组RAM 中。通过2 组RAM的复用,不仅减少了外部通信次数,同时减少了FPGA 片上RAM 资源的消耗。

图12 RAM 资源复用
2.4 通信调度
通过DMA的方式,以AXI FIFO 实现数据的传输,如图13 所示。由于RAM 组入口数据位宽为384 bit,而FIFO 传输数据位宽为64 bit,因此需要对位宽进行转换。同时,通过增加的FIFO 和位宽转换模块,使算法的实现与数据之间进行解耦合,各模块操作的端口相互独立,最大化地减少各模块之间的相关性,从而降低布线路由的复杂度。然后,以AXI BRAM 实现控制信号的传输,并在解析后完成对Kyber 蝶形运算单元阵列的调度控制。
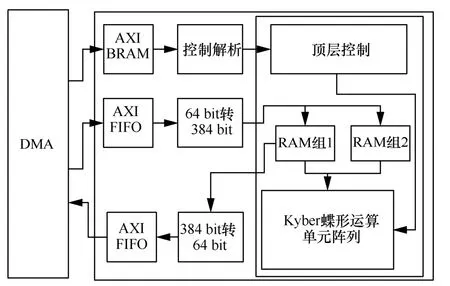
图13 DMA 通信调度
具体地,Kyber 算法的通信调度流程如下。
1) 通过DMA 对RAM 组1 和RAM 组2 进行参数配置;
2) 由NTT 使能信号,按先A(x)再B(x)进行NTT计算,并将结果保存在对应的RAM 组1 和RAM组2 中;
3) 由CWM 使能信号,从RAM 组1 和RAM组2 中读取数据,完成CWM 计算,并将结果保存在RAM 组1 中;
4) 再由控制信号完成INNT运算,并写入RAM组1;
5) 最后,将结果由DMA 传出。
3 实验结果与分析
3.1 实验环境
本文实验的硬件平台为FPGA 加速卡,芯片型号为Xilinx公司的xc7z035ffg676-2,其查找表(LUT,look up table)资源是171 900,触发器(FF,flip flop)资源是343 800,块RAM(BRAM,block RAM)存储器资源是500,数字信号处理器(DSP,digital signal processing)资源是900。软件平台为集设计、仿真、综合、布线、生成于一体的Vivado 2019.2软件。
首先,实验通过对算法的各模块进行深度优化,给出了综合布线后的资源占用情况。其次,通过仿真分析了各模块计算周期,并在可运行的最高频率下,给出了硬件的具体性能和能效比。最后,与其他Kyber 算法设计方案进行了综合对比,并对结果进行了分析说明。
3.2 各模块实现
Kyber 算法中各模块资源占用如表2 所示。其中蝶形运算单元以流水线方式实现;控制单元以串行方式实现;多RAM 通道以并行方式实现;ROM存储以串行方式实现。Kyber 算法通过串并混合设计,提高整体计算性能。

表2 Kyber 算法各模块资源占用
从表2 中可以看出,蝶形运算单元占用资源较少,且仅消耗了一个DSP 即可完成乘法运算。而控制单元消耗了更多的LUT 资源,这是因为需要计算各种计数、地址及控制信号使能,包括蝶形运算轮次、本轮迭代次数、RAM 和ROM的读写地址、读写使能信号及等待控制等。其次,对于多RAM通道和ROM 存储,需要存储Kyber 算法计算过程中的全部参数,仅消耗了FPGA 部分BRAM 资源。最后,对于Kyber 整体实现,通过Vivado 软件综合布线后,LUT 资源占用比例为8.51%,FF 占用为1.66%,BRAM 占用为13.80%,DSP 占用为3.56%,资源消耗适中。
3.3 性能分析
描述Kyber 算法硬件平台的指标有性能、功率、能效比。其中性能指硬件平台单位时间内的密码计算速率,简记为speed。功率用于计算硬件设备工作时的能耗,简记为power。能效比表示平台性能与设备功率之比,简记为eer,计算式如下

Kyber 算法实现的各项硬件性能指标如表3 所示。其中,能效比计算对应的芯片功耗为1.088 W。从表3 中可以看出,利用FPGA 实现的Kyber 算法不仅性能达到了每秒百万级别的计算速度,且功耗较低,具有很高的能效比,适合在物联网、云计算、高性能计算等多种场景中使用。
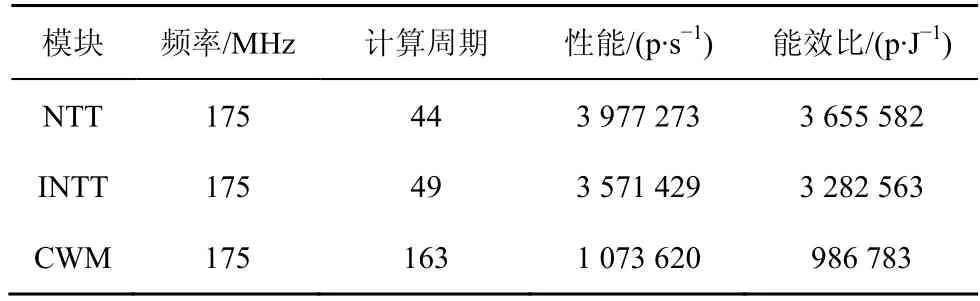
表3 Kyber 算法的各项硬件性能指标
3.4 与其他方案对比
电路面积与运算时间的乘积AT[17,19]客观反映了资源消耗和算法性能之间的关系。AT 值越低,表明在有限的资源条件下,与性能之间取得了更好的平衡。为了方便与其他方案对比,所有硬件实现均用AT 值进行归一化处理。
具体地,本文采用的AT 值计算式如下

其中,时间为执行一次NTT 运算所消耗的时间,即时间=NTT 周期/ 频率。
本文方案与其他Kyber 算法的FPGA 实现方案在NTT 周期、频率、资源消耗和AT 值等方面综合对比如表4 所示。
在表4 中,本文方案具有最短的计算周期。这是由于本文采用32 个蝶形运算单元并行执行,且工作在较高的频率,缩短了整体计算周期。同时,合理利用了芯片的DSP 和RAM 资源。在AT 值方面本文方案优于大部分方案,但差于文献[17]文案和文献[10]文案。文献[5]文案采用的是16 个蝶形运算单元,缩短了计算周期,但其模约简计算稍复杂,且消耗了更多的LUT 资源,AT 值稍高。文献[9]方案在FPGA 内放置了2 个蝶形运算单元,并支持CWM 运算,但程序仍以串行执行为主,导致NTT计算周期长,AT 值较高。文献[10]方案使用的是Xilinx 高端芯片,采用全新架构,资源密度是本文Zynq-7035的6.37 倍,其工作频率也是所有方案中最高的。该方案放置了4 个蝶形运算单元,并消耗了28 个DSP 完成模乘运算。由于其DSP 工作频率高,降低了模乘运算时间,AT 值也是最低的。但该方案的NTT 和INTT 各自独立实现,其INTT 还需要额外消耗60 个DSP,逻辑复用率低,占用了更多的资源。文献[12]方案以运算逻辑复用实现各步操作,占用资源最少,但导致并行程度低,NTT计算周期长,AT 值最高。文献[17]方案虽然具有较好的AT 值,占用资源少,但它采用了K2-RED 模约简算法,通过预计算的方式仅能实现NTT 和INTT 运算,无法直接实现CWM 运算。

表4 与其他FPGA 实现方案的综合对比
总体而言,本文提出的Kyber 算法的FPGA多路并行优化实现,至少缩短了36.23%的NTT 计算周期,并缩短了37.50%计算时间,在保证较高的工作频率下,充分利用了芯片逻辑资源,具有较优的AT 值。
4 结束语
基于格密码方案对于未来后量子密码标准,乃至对未来信息系统的安全都有至关重要的作用。本文通过对Kyber 格密码的描述,首先,深入剖析了NTT、INTT 及CWM 算法;然后,采用流水线技术实现了蝶形运算单元的优化,并以多通道RAM 优化参数存取,降低整体计算时延;最后,以32 个蝶形运算单元并行计算,实现了FPGA 整体架构,提高了计算效率。显然,本文实现方案具有很高的研究和实际应用价值。
在实际应用中,侧信道分析攻击仍是密码攻击的主要手段。因此,在硬件层面如何提供Kyber 格密码的安全防护策略,显得至关重要。这不仅增加了额外的资源消耗,且提高了设计难度,仍需要探索解决,也是未来的研究工作。
