基于编码矩阵结构特征的非删余极化码参数盲识别算法

王垚，王翔，杨国东，黄知涛

（1.国防科技大学电子科学学院，湖南 长沙 410073；2.陆军工程大学通信士官学校，重庆 400036；3.中国人民解放军92001 部队，山东 青岛 266023）

0 引言

为了实现稳定可靠的通信，信道编码技术被广泛应用于各类数字通信系统中，该技术的合理运用可以有效提高信息传输的质量。其中，极化码是已知的唯一一种被严格证明在二进制离散无记忆信道（B-DMC,binary discrete memoryless channel）下能够达到香农极限的信道编码方法[1]，并被确定为5G 增强型移动宽带（eMBB,enhanced mobile broadband）场景下的控制信道编码方案[2]。极化码是5G 通信中采用的新型编码方式，对其进行参数盲识别的研究，具有重要的研究价值。

在认知通信和非合作通信领域，信道编码盲识别受到了国内外越来越多的关注。从编码过程上看，极化码属于线性分组码，且当前线性分组码盲识别课题已经有了较多的研究成果与积累。文献[3]利用接收码字的秩特性，提出一种基于秩准则的编码类型识别算法。文献[4]提出一种基于游程特征的线性分组码与卷积码类型识别算法，该算法可以较好地对线性分组码与卷积码进行区分。针对循环码识别问题，文献[5]从循环码定义出发，利用欧几里得算法，完成循环码生成多项式的识别。文献[6-7]利用循环码生成多项式为xn+1的因子这一特性，通过因式分解实现循环码识别，但误码适应能力不足。针对BCH（Bose-Chaudhuri-Hocquenghem）码识别问题，文献[8]提出了一种利用码根差熵和码根统计的本原BCH 码识别算法，但在高码率情况下识别性能变差，且算法计算量较大。文献[9]提出了一种基于伽罗华域傅里叶变换（GFFT,Galois field Fourier transform）的识别算法，通过算法的优化避免了错误码字对识别结果的影响，误码适应能力得到提高。文献[10]首次引入软判决序列对本原BCH码进行识别，通过计算码字多项式的码根 KL（Kullback-Leibler）散度，利用码根概率分布识别出码长、本原多项式以及生成多项式，识别性能得到较大的提高。针对RS（Reed-Solomon）码识别问题，文献[11]提出了基于伽罗华域中高斯消元的识别算法，该算法在码长较短的情况下具有一定实用性，但是计算复杂度会随着码长增加而急剧增加，且容错性能较差。文献[12]从提高容错性能出发，提出基于GFFT的识别算法，虽然算法容错性能得到了提升，但运算量随着码长增加会急剧增加。文献[13]建立了基于似然判决的二元域统计判决模型，引入了能够衡量校验关系成立大小的平均校验符合度概念，通过遍历的方式对参数进行匹配，该算法具有较好的低信噪比适应能力。此外，针对卷积码[14-15]、低密度奇偶校验（LDPC,low density parity check）码[16-17]、Turbo码[18-19]等不同编码方式的识别问题，也有大量的研究。

由于极化码特有的编码理论与方法，传统的线性分组码识别算法并不适用于极化码，且目前针对极化码识别的研究较少。其中，文献[20]通过对信道删除概率和极化码码长进行遍历，求得对应的生成矩阵及其零空间，并利用零空间对硬判决码字矩阵依次进行校验，确定编码参数。文献[21]通过对码长和冻结比特进行遍历，依次选取冻结比特求得所对应的对偶向量，利用对偶向量对软判决码字矩阵进行校验，判断码字是否选取该比特作为其冻结比特，但在对统计量计算的过程中进行了近似处理。现有算法由于未有效利用极化码的相关性质，均需要采用参数遍历的方式对参数空间进行搜索，得到参数的估计值，导致算法过程较复杂、计算量较大，同时在计算过程中采用硬判决序列或对统计判决量进行近似，算法的误码适应能力不足。

针对上述问题，本文同样对标准非删余极化码的编码过程展开了研究。通过对极化码相关性质的研究，证明了描述极化码生成矩阵、码长、信息比特和冻结比特之间特有关系的定理与命题；利用信息比特的分布规律，实现码长的识别；引入似然差（LD,likelihood difference）作为检验关系的判决统计量，并从理论上分析了似然差的统计特性，基于最大最小准则对最优判决门限进行了求解，实现信息比特与冻结比特的识别，对码率进行估计。所提算法充分利用了极化码生成矩阵的结构特征，在保证识别性能的前提下，显著降低了运算量。仿真证明了所提算法的有效性。若无特殊说明，下文极化码均指标准极化码。

1 信道极化

极化码的产生来源于信道极化理论。对于一个二进制离散无记忆信道W:X→Y，其转移概率为W(y|x)，x∈X，y∈Y。信道极化的过程包含2 个阶段：信道合并和信道分裂。信道合并是指N个独立信道经过线性变换合并为信道W N:XN→YN，信道分裂则是将信道WN分解成N个子信道。图1 为标准极化码一级信道结构，将2 个比特进行编码，可得

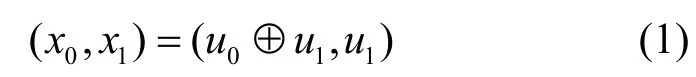
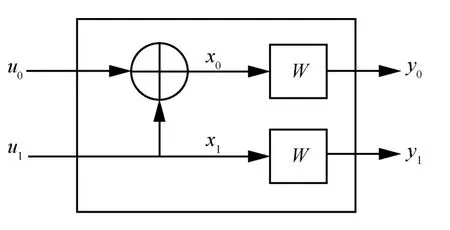
图1 标准极化码一级信道结构

将0x和1x分别通过信道W进行传输，得到y0和1y，则合并后的信道2W的转移概率为

多级级联进行上述操作，最终可以实现多级极化。经过n=lbN次极化后，得到的合并信道WN的转移概率[1]为

其中，BN表示比特逆序重排矩阵，FN=⊗nF，，⊗表示Kronecker 积。对于非标准极化码，也可采用3 ×3 或更高阶次的核F。分裂后的子信道的转移概率[1]为

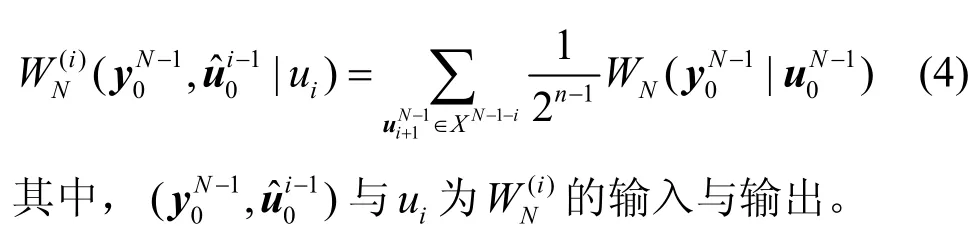
1.1 极化信道可靠性估计

对于二进制删除信道（BEC,binary erasure channel），为描述极化信道的可靠性，可以引入巴氏参数[1]作为表征信道W质量的参数，其定义为

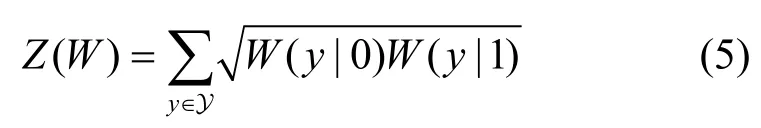
当信道W只用来发射单个比特时，巴氏参数是使用最大后验概率判决时错误概率的上界。当信道为BEC 时，Z(W) 可以通过式(6)计算得到[1]。

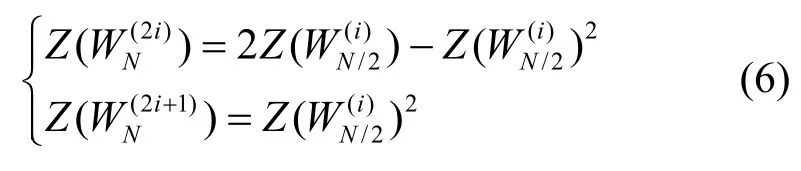
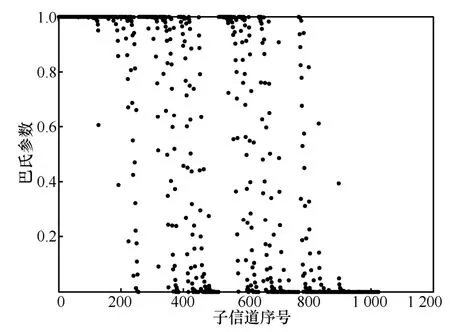
图2 BEC 子信道巴氏参数分布

1.2 极化码编码

极化码利用可靠性较高的子信道来传输有用的信息比特，而利用可靠性较差的子信道传输冻结比特。极化码的编码过程用生成矩阵的形式可以表示为

其中，u1×N为原始比特序列，c1×N为编码后的比特序列，GN为生成矩阵，2n N=为码长，n为正整数。生成矩阵表示为

容易证明，生成矩阵GN是一个N×N维的满秩矩阵，其行向量与子信道一一对应。假设A是一个元素个数为k的正整数的集合，A中每个元素为信息比特所对应子信道的行标号，则其补集cA中的元素为冻结比特所对应子信道的行标号，码率为。uA为要传输的信息比特，为冻结比特，于是编码过程可表示为

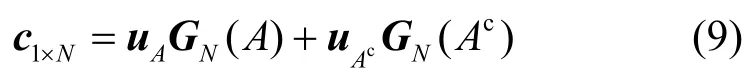
一般情况下，极化码的冻结比特均取0，此时编码过程可进一步简化为

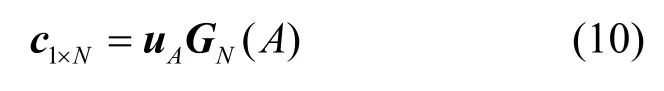
由极化码编码原理可知，当给定编码长度，极化码的编译码结构将被唯一确定，且可以通过生成矩阵的形式表示编码过程。由此可知，标准非删余极化码识别最终目的是完成对极化码码长、信息比特及冻结比特的识别。通常在实际通信系统中，采用线性分组码的比特流序列通常有固定的帧结构和相应的同步码[21]，且已有相应方法能够实现对帧同步码的盲识别[22-23]，故本文假设已完成帧同步，集中对极化码参数识别问题进行讨论。除特别说明外，本文矩阵运算均在二元域F(2) 上进行。

2 极化码识别原理与算法

2.1 识别原理

根据极化码编码原理可知，标准非删余极化码码长通常为2n（n＞0 ），不同码长的极化码对应着不同的生成矩阵GN。在给出具体的识别算法之前，首先对矩阵GN的相关性质进行研究，给出相关的定理及命题，作为极化码参数识别算法的理论基础。

定理1对于矩阵F⊗n，具有如下性质

定理1 利用数学归纳法易证得。根据定理1可知，对于矩阵F⊗n，当剔除其第i行后，记得到的新矩阵为，矩阵的对偶向量即F⊗n的第i列。根据极化码编码性质可知，生成矩阵GN与矩阵F⊗n由相同的行向量组成，只是行向量的排列顺序不同，其对应关系由矩阵BN所决定，易证得

考虑码长为N=2n、码率为k/N的极化码，当码字(c1,c2,…,cN),…,(c(L-1)N+1,c(L-1)N+2,…,cLN)被拓展为(c1,c2,…,cN,…,c(L-1)N+1,c(L-1)N+2,…,cLN)时，拓展后的码字等价于码长为LN(L=2m)的新极化码，拓展后的极化码生成矩阵可记为=IL⊗GN，其中IL为维数为L×L的单位矩阵。

命题1对于拓展后码长为LN(L=2m)的新极化码，记其对应的（n+m）次克罗内克积为F⊗(n+m)，生成矩阵为，则有

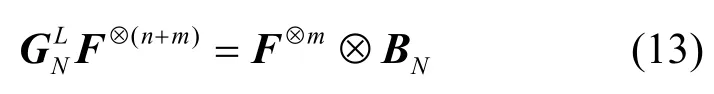
证明

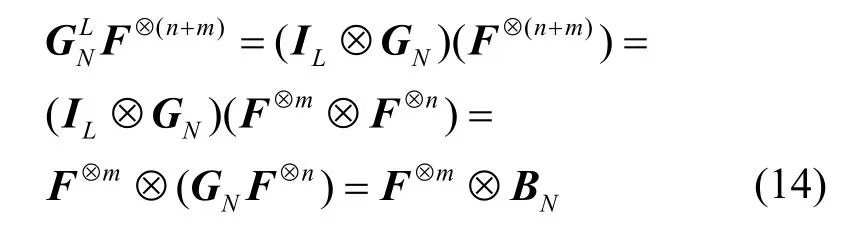
证毕。

2.2 冻结比特与信息比特识别

假设接收到的码流序列共包含M个完整码字，记为r，其中N满足2n N=。考虑命题1 中m=1 时的情况，即码字矩阵的设定码长与真实码长相等，利用截获的码流序列r构建码字矩阵R

在无误码条件下，根据式(10)，接收到的码字可表示为R=C=UGN(A)，其中U为对应的信息矩阵。记码字矩阵R与矩阵⊗nF相乘所得矩阵为Φ。

命题2在无误码条件下，矩阵Φ中零列向量的数量为n-k，零列向量的位置与冻结比特的位置一一对应。

证明对于矩阵R与矩阵⊗nF，可得

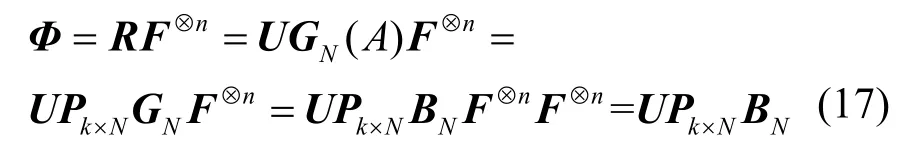
其中，矩阵Pk×N为行满秩矩阵，用于选出GN中行标号属于集合A的行。考虑到矩阵BN为行置换矩阵，每行每列有且仅有一个元素为1，行与行之间、列与列之间1的位置均不同，可将式(17)化简为

根据极化码编码性质可知，生成矩阵GN与矩阵F⊗n中行向量所处位置的对应关系由矩阵BN决定。因此根据命题1 可知，当剔除生成矩阵GN第i行后得到矩阵，存在由BN决定的变换π(·)，使矩阵的对偶向量为F⊗n的第π(i)列。则信息比特和冻结比特所对应子信道的行标号集合分别为A={π-1[α(1)],π-1[α(2)],…,π-1[α(k)]}和Ac={π-1[b1],π-1[b2],…,π-1[bN-k]}。证毕。

因此，根据命题2 可知，当码字矩阵设定的码长与真实码长相等时，只需要考察码字矩阵R与矩阵F⊗n各列之间的校验关系，并利用映射关系π(·)即可求得集合A。当矩阵F⊗n第i列与码字矩阵R不满足校验关系时，π-1(i)为集合Ac中的一个元素，否则π-1(i)为集合A中的一个元素。同时，码率估计值为

2.3 码长识别

根据2.2 节分析可知，当码字矩阵设定的码长与真实码字长度相同时，利用码字矩阵R与矩阵F⊗n的运算结果，可以实现信息比特和冻结比特置的识别。但实际接收中，无法事先知道极化码码长，因此本节将继续对码长识别进行分析。

首先，考虑无误码情况。当码字矩阵设定的码长大于真实码长时，即N′=LN=2n+m（m＞ 1），可构造码字矩阵RL。此时码长为N=2n、码率为k/N的极化码，被拓展为码长为LN(L=2m)的新极化码。接收到的码字矩阵可表示为R L=其中UL为对应的信息矩阵。记码字矩阵RL与矩阵F⊗(n+m)相乘所得矩阵为ΦL。

命题3在无误码条件下，矩阵ΦL中零列向量的数量为(n-k)L，且周期性出现，周期为N。

证明根据命题1 与式(17)可得

根据2.2 节分析可知，矩阵Γ的任意一行γi的元素，只有在α(i)的位置为1，其他位置均为0。因此，矩阵F⊗m⊗Γ将周期性出现零列向量，周期为N。证毕。

根据命题3 可知，矩阵F⊗(n+m)中与码字矩阵RL满足校验关系的列将周期性出现，其周期与码长、矩阵F⊗(n+m)存在严格约束关系。因此，当接收码字不存在误码时，选择合适的码长并计算矩阵ΦL，根据矩阵中零列向量的分布情况可以得到码字矩阵设定的码长与真实码长之间的关系，计算出真实码长。

但当接收序列存在误码时，码字矩阵RL与矩阵F⊗(n+m)之间的校验关系将被破坏。另一方面，对于矩阵F⊗(n+m)中码重较重的列向量而言，由于码重较大，也更容易受误码影响，导致校验关系失效。

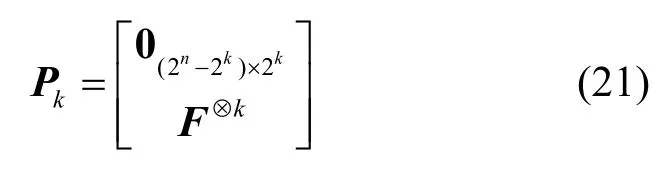
根据矩阵F⊗n构造原理可知，F⊗n满足性质

因此，将F⊗n的后2k列（k=2,…,n）记为Pk，则有

即码字矩阵RL与矩阵F⊗(m+n)进行校验关系检测时，其后2k个校验值，等价于码字矩阵与矩阵F⊗k进行校验关系的检验。因此，可将矩阵F⊗k中未通过正交检验的列的数量与2k的比值，作为码字矩阵码长为2k时的等效极化码码率估计值，记为。根据文献[21]中定理1 可知，在无误码情况下，当码字矩阵设定的码长小于真实码长时，等效极化码码率将大于真实码率；当码字矩阵设定的码长大于或等于真实码长时，其将等于真实码率。但又由于误码的影响，部分校验关系将被破坏，使通过检验的冻结比特减少，码率增加。因此在误码条件下，当码字矩阵设定的码长等于真实码长时，所求得码率ˆη为最低码率，可利用该性质判断极化码码长。

2.4 校验关系检测

在实际信息传输过程中，码字会受到噪声的影响而产生误码，由于硬判决序列只包含序列判决结果，而软判决序列不仅能提供0/1 比特数据，还能额外提供判决序列的可靠性信息。因此，本文采用软判决序列进行处理，对编码参数进行识别。为与前文区分，由软判决序列构成的码字矩阵记为TL。

假设信号采用二进制相移键控（BPSK,binary phase-shift keying）调制，在加性白高斯噪声（AWGN,additive white Gaussian noise）信道条件下，其中ni,j为均值为0、方差为2σ的高斯白噪声序列，si,j为BPSK 调制符号，与原始码字ci,j之间满足

引入对数似然比（LLR,log-likelihood ratio），定义为[24]

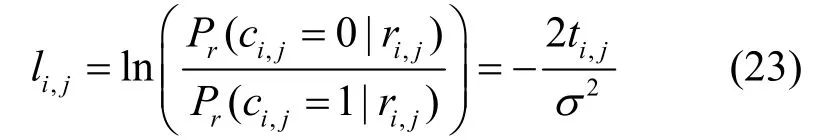
记矩阵F⊗n中第j列为fj，为了研究码字与fj的校验关系，单独取码字矩阵TL第i行ti进行研究，此时对应的码字为ci，可以将式(23)进行推广得到ci与fj正交的对数似然比为

其中，fj=[f1,j,f2,j,…,fN,j]T，ti=[ti,1,ti,2,…,ti,N]，ci=[ci,1,ci,2,…,ci,N]，lj,t为fj第t个非零值的索引。在计算LLR 时，需要多次进行较复杂的双曲正切及其反函数的运算。为降低运算量，引入似然差LD来替代LLR，其定义为[25]

考虑以下两类假设检验。

H1：fj与极化码码字构成校验关系。

H0：fj与极化码码字不构成校验关系。

设wt=weight(fj)，即向量fj中含有wt个“1”。当校验关系成立时，意味着码字ci中下标为{lj,t}的码元中应有偶数个码元为“1”，共有种可能。因此，当H1成立时，LDj的均值和方差分别为

当H0成立时，由于码字与向量jf之间不存在校验关系，LDj的均值和方差分别为

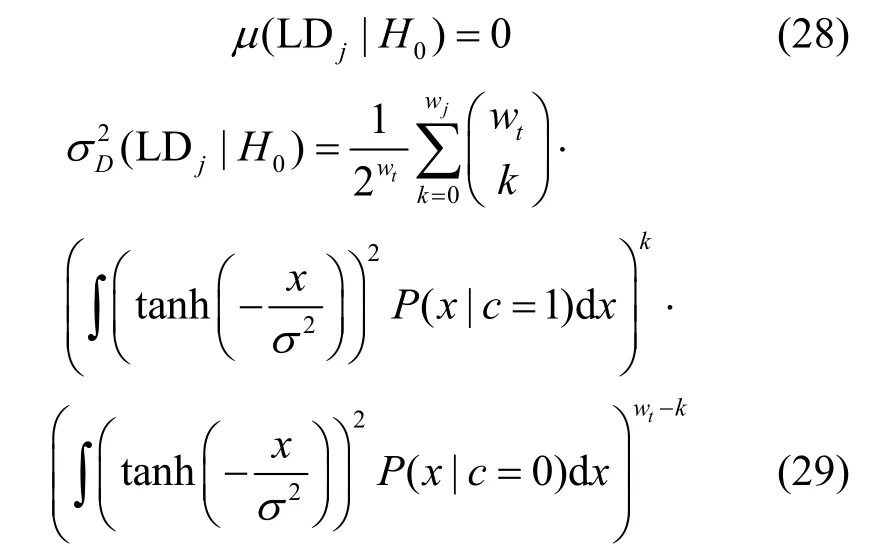
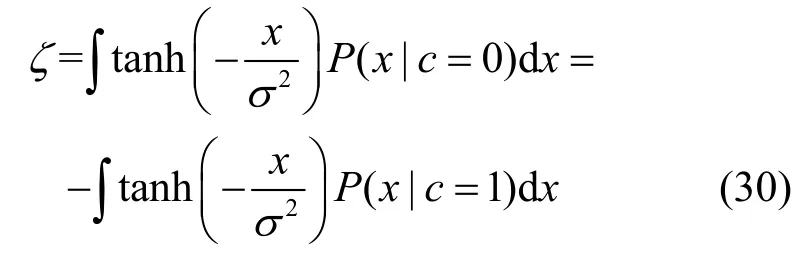
代入式(26)可得

同理可得

式(31)～式(33)只考虑了第i个码字的似然差，将码字矩阵的所有行考虑进去，则可得到平均似然差，即

设两类假设的判决门限为Λ，由于在非合作通信系统中无法获得两类假设的先验信息，因此本文采用极小化极大准则来求解门限Λ。同时，假定正确判断的代价因子取值为0，错误判断代价因子取值为1。根据极小化极大准则可知，门限Λ需满足

解得门限为

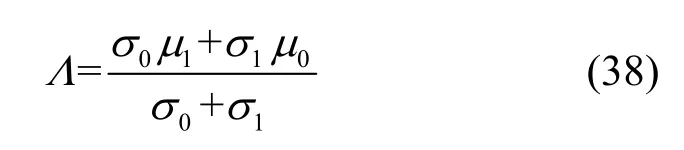
根据设定的码长，利用截获的数据构造出码字矩阵，然后依次利用矩阵中列向量与码字矩阵进行校验，计算出统计校验量与对应的门限Λ。当统计校验量大于门限时，则认为该位置为冻结比特，反之则为信息比特。

2.5 识别算法流程

由前文分析可知，合理设定接收码字矩阵的码长值，构建码字矩阵LR与矩阵，依次对码字矩阵LR与矩阵后2k（k=2,3,…）列之间的校验关系进行检验，当某一个列向量的校验关系成立时，矩阵GN中与其对应的行即冻结子信道的所在行。然后计算等效极化码码率的估计值，对码长、码率进行估计，即通过一次计算完成参数的识别，而不需要像现有算法需要对所有可能码长进行遍历，有效降低运算量，具体如算法1 所示。

算法1基于编码矩阵结构特征的极化码参数识别算法

3 仿真分析

考虑到5G 通信中增强移动宽带场景下控制信道编码方案，确定采用的极化码最大母码长度在下行控制信道中为512，在上行控制信道中为1 024，最低码率为1/8。因此，仿真设定极化码码长分别为32、64、128、256、512、1 024，最大码长为1 024。不失一般性，设噪声环境为AWGN 信道。

3.1 统计模型验证

本节主要对前文推导的似然差统计特性进行验证。前文在推导似然差分布函数的过程中进行了一定假设，其正确性是算法有效求解判决门限的前提条件。根据矩阵的构造规律可知，其列向量的码重取值集合为{ 2k|k∈{1,2,…,nmax}}。仿真设定了4 种码重值，分别为32、64、256、1 024。设定的信噪比范围为-10～12 dB，步长为0.5 dB。利用均值与方差的定义，仿真求得在不同条件下平均似然差的均值与方差，并和理论推导计算得到的均值与方差进行对比。

从图3 中可以看出，在不同假设条件下，利用定义所求得的均值与方差和理论计算得到的值几乎完全重合，证明了前文中对于似然差分布函数推导的正确性。其中，图3(b)中的方差曲线在某信噪比下出现峰值，其原因是当H1成立时，矩阵中任意列向量fj的似然差均值为ζ，其方差为ζ可由数值计算求得，其取值范围为（0,1）。同时，对于函数f(ζ)=，当ζ∈(0,1)时，函数f(ζ)在ζ=时取得极大值0.25。图3(b)的横坐标为信噪比，而随着信噪比的提高，ζ值逐渐趋近于1，因此方差曲线会在某一信噪比时取得峰值。图4 为wt取不同值时函数f(ζ)=在（0,1）的取值。

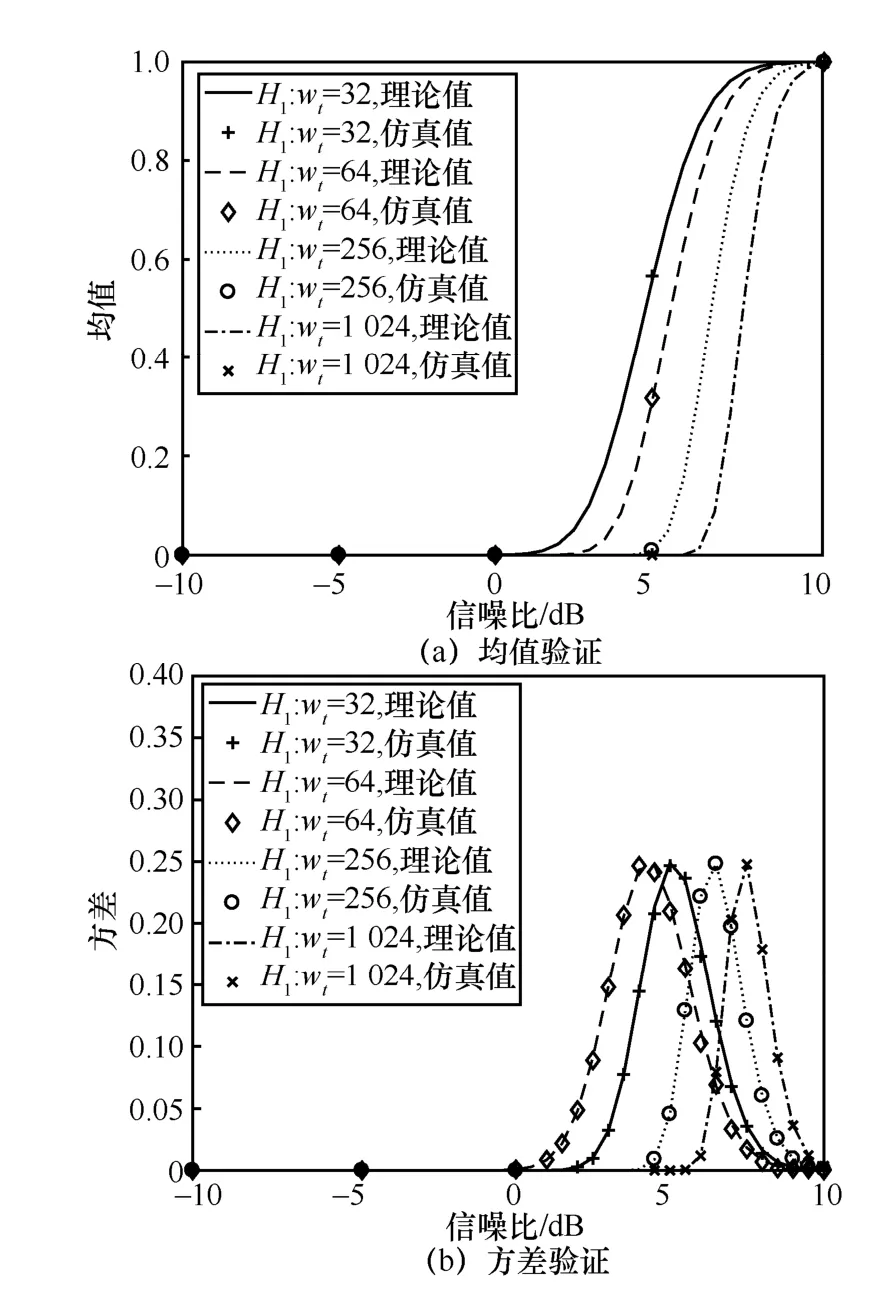
图3 似然差统计特性对比

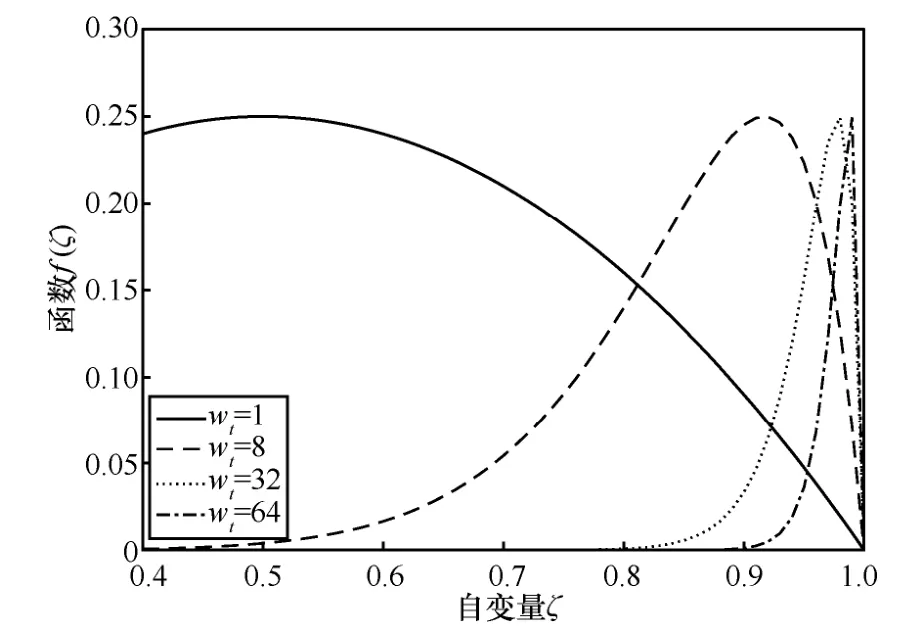
图4 wt 取不同值时函数 f (ζ) 在（0,1）的取值

3.2 算法有效性验证

本节主要利用仿真对命题1 及算法的有效性进行验证。本节所采用极化码码率为1/2，码长为64，设定的最长码长2nmax为128。信噪比分别取5 dB 和0，设定码字个数为2 000 个。在2 种信噪比条件下，记录不同列的平均似然差值和门限，以及不同码字矩阵码长的等效码率。不同信噪比下的平均似然差与门限及判决结果分别如图5 和图6 所示。

图5(a)给出了不同列的平均似然差和对应的判决门限。当似然差大于门限时，判定校验关系成立，该列向量对应的π-1(i)为冻结比特，否则为信息比特。图5(b)则给出了似然差判决结果。从图5(b)可以看出，当信噪比为5 dB 时，接收信号的误码率较低，校验关系检测结果的序列中存在2 个完整的周期。同时，图5(c)中等效码率也随着码字矩阵码长的增加而降低，当n=5 时降到最低，与仿真设定值相对应，且与2.3 节分析结果一致。

图5 N=64，SNR=5 dB 条件下判决结果

当信噪比降到0 时，接收信号的质量下降，导致了更多的误判。从图6(b)中可以看出，判决结果前后两段已经不同，即由于误码的影响，判决结果出现了错误，周期性被破坏。从图6(c)可以看出，当码字矩阵码长小于真实码长时，码率大于真实码长的码率；当码字矩阵码长大于真实码长时，码率同样大于真实码长的码率，与2.3节的分析一致。

图6 N=64，SNR=0 条件下判决结果

3.3 容错能力验证

本节主要考察不同码字个数、码率对本文算法识别性能的影响，并对算法容错能力进行验证。

1) 码字个数对识别性能的影响

本节主要考察累计码字数量对算法的影响。仿真设定极化码码长为64，码率为1/2，设收到的码字数量分别为1 000、2 000、3 000、4 000，信噪比为-2～4 dB，间隔为0.5 dB，蒙特卡罗次数为500，统计不同信噪比下算法的识别率，结果如图7 所示。从图7 中可以看出，随着码字数量的增加，算法性能也有所增加，主要是因为随着码字数量的增加，所求得的平均似然差逐渐逼近理论值，使判决结果正确率更高，算法性能也随之提升。

图7 N=64 时不同信噪比下算法的识别率

2) 码率对识别性能的影响

本节主要考察码率对算法性能的影响。仿真设定极化码码长为64，码率分别设定为1/4、1/2、5/8、3/4，码字数量为2 000，信噪比为-2～4 dB，间隔为0.5 dB，蒙特卡罗次数为500，统计不同信噪比下算法的识别率，结果如图8 所示。从图8 可以看出，码率对于算法的识别性能影响不大。通过对极化码编码过程的研究发现，这主要是因为随着码率的变化，虽然信息比特数和冻结比特数随之改变，但高码率对应的对偶向量是低码率对偶向量的子集，且是低码率对偶向量中码重较重的部分，更易受误码影响。也就意味着，随着码率的降低，对偶向量集合元素不断增加，但增加的对偶向量码重较低，受误码影响较小，更易识别。综上所述，对识别性能影响较大的对偶向量是不同码率条件下对偶向量的交集，因此算法识别性能受码率的影响也较小。

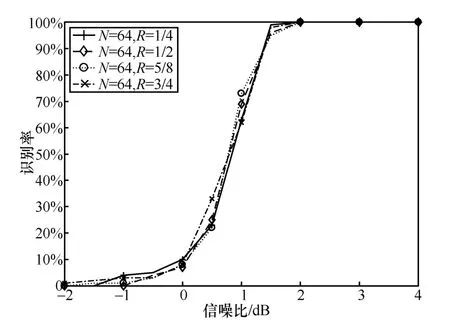
图8 M=2 000 时不同信噪比下算法的识别率

3.4 性能对比

本节主要考察码长对于识别性能的影响，并与现有算法的性能比较。仿真设定的目标码长为32、64、128、256、512、1 024，设定极化码码率为1/2，码字数量为2 000，信噪比范围为-2～8 dB，间隔为1 dB，蒙特卡罗仿真次数设定为500 次，统计不同算法在不同信噪比下的识别率，结果如图9 所示。

从图9 可以看出，随着码长的增加，算法识别性能逐渐下降。这主要是因为当码长增加时，码重也随之增加，同时需要识别的信息比特和冻结比特增加，更易受到误码的影响，单个码字中出现误码的概率也就更高。因此在相同条件下，随着码长的增加，识别难度逐渐增大，误判概率也就越大。从识别结果来看，当信噪比为6 dB 时，对于码长为1 024的极化码，所提算法能够达到接近100%的识别率，说明算法具有较好的误码适应能力。

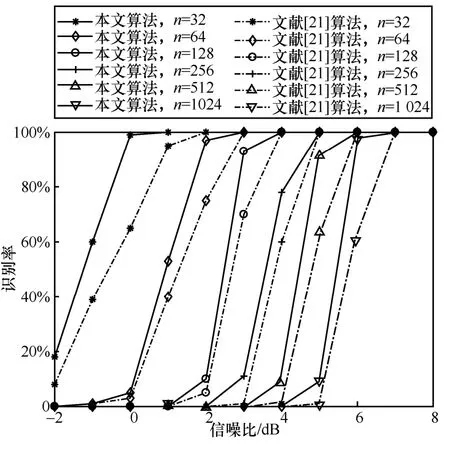
图9 不同算法在不同信噪比下的识别率

同时，图9 给出了与文献[21]算法的仿真对比结果，文献[21]算法的识别性能是现有最优的。从图9 中可以看出，本文算法在性能上有明显的提升，尤其是在信噪比较高时，本文算法能够较快地达到100%的识别率。文献[21]同样采用软序列作为处理对象，并采用对数似然系数作为统计判决量，但在计算对数似然系数时进行了近似处理，降低了运算精度。本文对于似然差的计算未做近似处理，且从3.1 节可以看出，本文推导的统计特性与实际情况一致，因此具有更好的识别性能。同时，在计算量方面，本文算法在计算似然差的过程中，有效利用了极化码生成矩阵的结构性质，与现有算法相比，不需要进行码长、码率等参数的遍历，有效降低了运算量，具体见3.5 节分析。

3.5 算法计算复杂度分析

假设接收到的软判决序列长度为L，最大码长为。首先，需要对每个判决值计算其似然差，在实际计算中已有多种高精度近似快速算法，其计算速度与乘法运算处于同一数量级[26]。本文仿真采用MATLAB 2016b 软件，在i7-9750H 处理器平台进行。在实际仿真平台运算中，测得计算似然差计算所需时间约为乘法的5 倍。在对⊗nF的每个列向量进行检验时，需要进行元素相乘和向量加法，共需要次乘法运算和次加法运算。同时，本文将门限计算等价为5 次乘法运算。对于本文算法，当真实码长为2n时，只需要计算个统计量，因此本文算法最大需要5L+次乘法运算和次加法运算。

文献[21]中所提统计量需要对每个判决值进行判断正负号和取模运算，各等价于一次加法运算，共需要2L次加法。计算每个统计量时，需要进行元素相乘、计算向量元素最小值和向量加法运算，其中比较大小可等价为一次加法，共需要L次乘法运算和次加法运算。对于不同的码长2n，均需要计算2n个统计量。同时，其门限计算可等价为10 次乘法运算。最后，对不同码长的计算量进行求和，最终为乘法运算和次加法运算。不论码长大小，所需计算量为固定值。

综上，本文算法计算复杂度更低，尤其是在码长较小的情况下。

4 结束语

本文对标准非删余极化码盲识别问题进行了研究，推导证明了生成矩阵、码字矩阵分别与克罗内克矩阵之间的约束关系，以及不同参数对该校验关系的影响，并基于以上性质提出了一种极化码盲识别算法。所提算法选择软判决序列进行处理，引入平均似然差作为判决统计量，能够有效利用软判决序列中的置信度信息，具有良好的误码适应能力。同时，算法有效利用了极化码生成矩阵的结构性质，采用了一种新的识别策略，不需要对所有可能的码长进行遍历，所需计算量低于现有软判决处理算法。仿真结果表明，所提算法识别性能优于已有算法，工程实用性更强。后续研究主要针对非标准删余极化码，并考虑冻结比特不为零的场景，以完善极化码盲识别问题的研究。