多臂机提综臂辅助旋铆并联机器人优化设计

2022-03-10梁正宇畅博彦徐振宇

工程设计学报 2022年1期

梁栋，梁正宇，畅博彦，齐杨，徐振宇

（1.天津工业大学机械工程学院，天津 300387；2.天津工业大学天津市现代机电装备技术重点实验室，天津 300387；3.天津职业技术师范大学机械工程学院，天津 300222；4.江苏金龙科技股份有限公司，江苏苏州 215500）

在实际工程应用中，多臂机常用于较为复杂的小花纹织物的织制。提综臂是多臂机上实现凸轮开口运动的关键核心部件之一［1］。现阶段对提综臂的加工大多是通过人工旋铆的方法将提综臂的相关零部件进行连接。若能实现旋铆工艺的自动化，则对于提高提综臂的生产效率和保证其加工质量均有至关重要的意义。基于此，笔者拟从多臂机提综臂辅助旋铆作业的工程需求出发，针对其部分加工过程，基于先进机器人技术提出一种可实现提综臂自动化生产的方案。

根据实际工程需求，提综臂的自动化装配工艺过程可具体分解为以下动作：1）从传送带上抓取零件；2）根据零件特征将零件放置于专用夹具内；3）将放置好的零件移至加工工作台；4）将装配完成的提综臂组件取出并重新放到指定传送带上。

相较于传统的串联机器人，并联机器人具有速度快、刚度大、结构稳定、运动惯性小、精度高、承载能力强和误差累积小等显著优势［2-3］。但是，并联机器人也存在工作空间小、奇异位形点多和关节间耦合性较强的缺陷。故为了获得较好的运动性能，以最大限度地发挥并联机器人的优势，进而满足实际工程需求，须对其进行优化设计。并联机器人的性能评价指标通常借助雅可比矩阵的代数特征来构造［4］。李占贤［5］和张良安等［6］基于运动雅可比矩阵的条件数，引入条件数全域均值与全域波动量来定义全域综合性能评价指标，并分别构建了Diamond和Delta并联机器人的尺度综合模型，获得了机器人机构的最优尺度参数；刘卓等［7］基于有限和瞬时旋量法构造了虚功率传递率指标，并对Exechon并联机器人的运动性能进行了评价；宋轶民等［8］基于瞬时旋量理论构造了功率传递系数，用于评价空间两转动并联机构的运动传递性能，并对其开展了尺度参数综合。

通常情况下，所建立的优化模型是非线性的，一般可采用经典的优化算法进行求解，如：目标达成算法（goal attainment method，GAM）［9］、序列二次规划（sequential quadratic programming，SQP）算法［5］等。然而，上述经典算法对初始值敏感，难以保证优化结果的全局收敛性。随着计算机科学和人工智能技术的快速发展，解决优化问题的智能算法不断涌现，例如神经网络算法、遗传算法（genetic algorithm，GA）［10］、粒子群优化（particle swarm optimization，PSO）算法［6，11］和蝗虫优化算法（grasshopper optimization algorithm，GOA））［12］等。智能优化算法可实现全局寻优，被广泛应用于并联机器人等复杂机构的优化设计。

面向多臂机提综臂旋铆加工的工程需求，结合并联机器人的优点，笔者拟设计一种新型辅助旋铆并联机器人，以实现提综臂的高效自动化生产。首先，采用旋量理论来解析机器人机构的拓扑结构；然后，建立机器人机构的运动学模型，并基于雅可比矩阵的代数特征来定义其运动性能评价指标，同时计及机器人的几何及传动性能约束，构建其尺度综合模型；接着，借助PSO算法对机器人进行运动学优化设计；最后，根据实际工程需求，利用ADAMS（automatic dynamic analysis of mechanical systems，机械系统动力学自动分析）软件对优化后的机器人机构进行多体仿真验证。

1 辅助旋铆并联机器人的结构及自由度分析

1.1 拓扑结构分析

新型辅助旋铆并联机器人机构主体部分的虚拟样机模型如图1所示（为便于观察，仅示意机构主体部分，其余附件未示出），其主要由左、右2条相同的支链组成。各支链中的肘部连接架上端通过连杆和转动副与基座（图中未示出）相连接，构成平行四连杆机构；其下端与动平台通过1组4U（U表示虎克铰）子链相连接，构成闭环结构。2条支链中的平行四连杆机构的大臂各由1台伺服电动机驱动，运动时可保证肘部连接架的姿态恒定，便于实施运动控制。在4U闭环子链中，任意被动杆的上端虎克铰的近架轴线（位于肘部连接架上）与下端虎克铰的远架轴线（位于动平台上）相互平行；上端虎克铰的远架轴线（位于被动杆上）与下端虎克铰的近架轴线（位于被动杆上）相互平行。动平台的形状为矩形，动平台上虎克铰的远架轴线共面，并关于动平台中心对称，且各自与动平台的边呈一定夹角。为不失一般性，可将动平台形状设计为正方形，并将位于动平台上的虎克铰的远架轴线与其边长的夹角设计为45°。

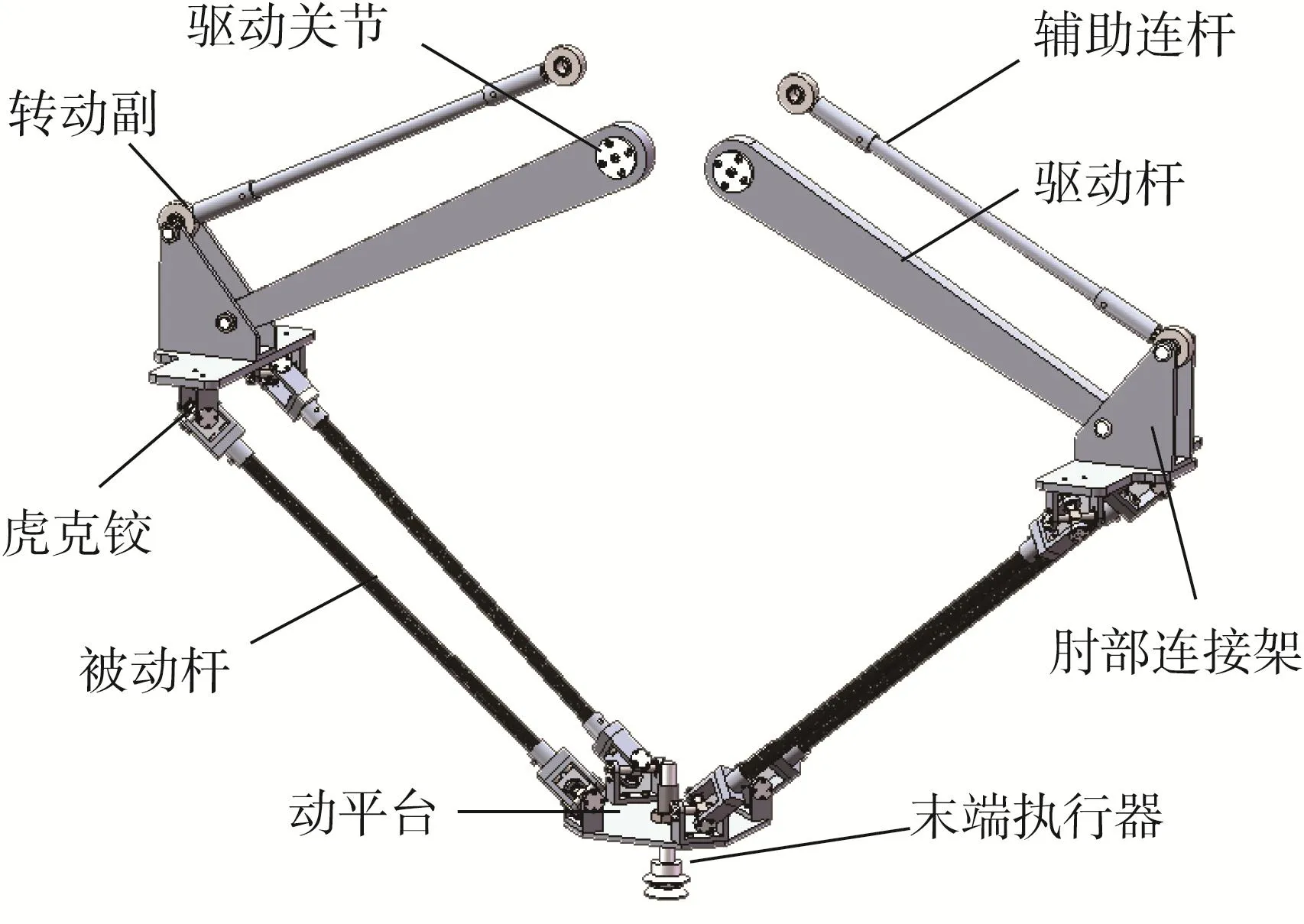
图1 辅助旋铆并联机器人机构主体部分的虚拟样机模型Fig.1 Virtual prototype model of main part of assisting-riveting parallel robot mechanism

1.2 基于旋量理论的自由度分析

新型辅助旋铆并联机器人机构的每条支链中同时包含平行四连杆机构（Ⅰ）及4U闭环子链（Ⅱ），其为过约束机构，仅运用经典的G-K（Grübler-Kutzbach）公式［13］无法准确地判断该机构自由度的类型和数量。因此，本文结合旋量理论［14-16］和修正的G-K公式对该机构的自由度进行详细分析。鉴于该机器人机构的2条支链结构对称，故不失一般性，在此取单条支链进行分析，如图2所示。其中，ζj(j=1，2，…，12)表示各转动关节轴线。

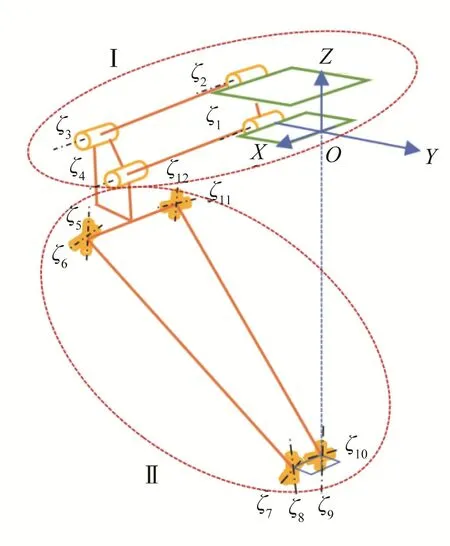
图2 辅助旋铆并联机器人机构的单条支链示意Fig.2 Schematic diagram of single branch chain of assisting-riveting parallel robot mechanism

平行四连杆机构可简化为广义运动副（Pa副），故整条支链可看作由广义运动副Pa与4U闭环子链串联而成。建立如图3所示的坐标系O-XYZ，其中X轴垂直于由平行四连杆机构的4个转动关节中心所张成的平面。

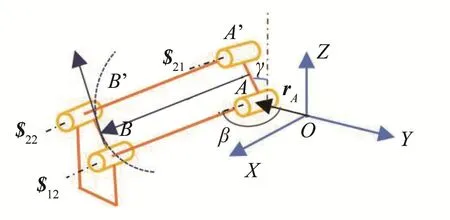
图3 平行四连杆机构结构简图Fig.3 Structure diagram of parallel four-bar linkage

在平行四连杆机构中，固定杆为AA’，输出杆为BB’，其中A点的位置向量为rA，杆AA’与Z轴的夹角为γ，杆AB与Y轴的夹角为β，由此分别得到杆AB与杆A’B’的运动旋量系：

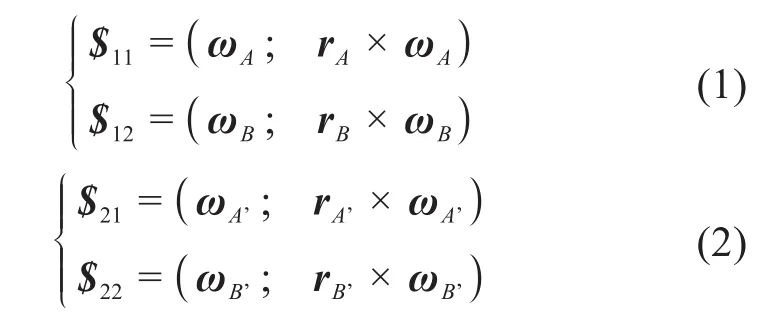
式中：ωA、ωA’、ωB和ωB’分别为各转动关节的转轴基矢量，且ωA=ωA’=ωB=ωB’=ω。

鉴于平行杆件的长度相等，即lAA’=lBB’=l1，lAB=lA’B’=l2，可得：

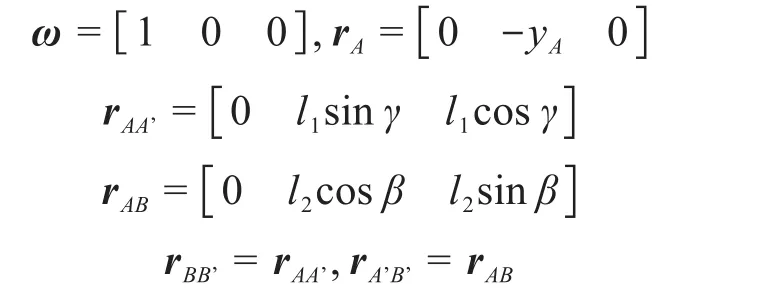
其中：yA为A点到XOZ平面的距离。

根据旋量互易积概念［14-15］，可分别求得杆AB与杆A’B’的反旋量系（即约束旋量系），表示为：

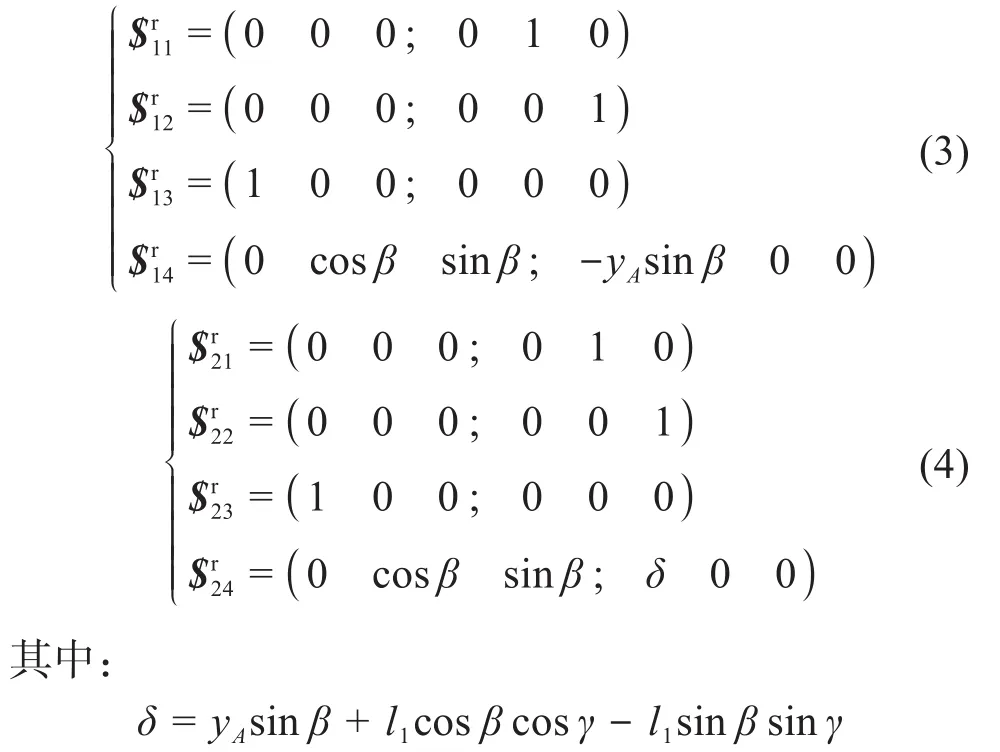
将上述2个约束旋量系组合成一个新的集合，求出1组基，得到平行四连杆机构的约束旋量系：

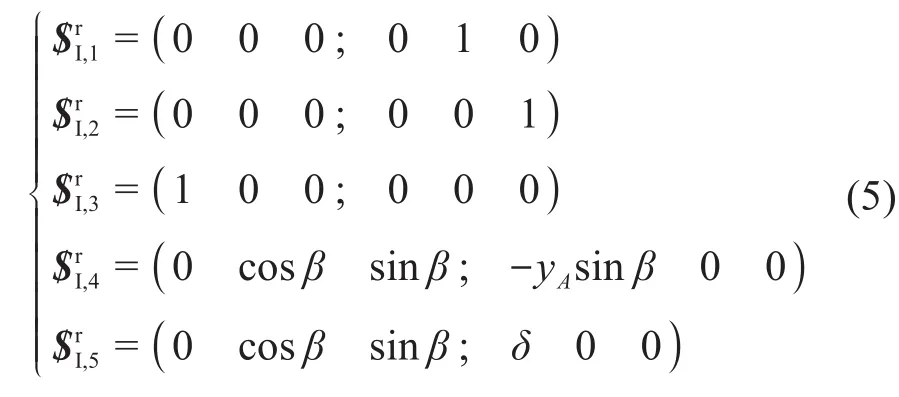
基于式（5），可求得杆BB’的运动旋量：

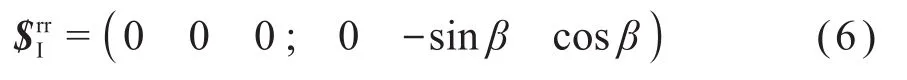
由此可知，杆BB’具有1个沿圆弧（半径为l1）切线方向的移动自由度，因此其等效可为在YOZ平面内的移动副。

基于相同的参考坐标系，对4U闭环子链进行分析。4U闭环子链可视为由DE和D’E’这2个U-U分支构成的并联机构，如图4所示。由于DE和D’E’分支结构对称，故在计算这2个分支的约束旋量系时，约定在DE分支中k=1，在D’E’分支中k=-1。为不失一般性，以DE分支为例进行分析。

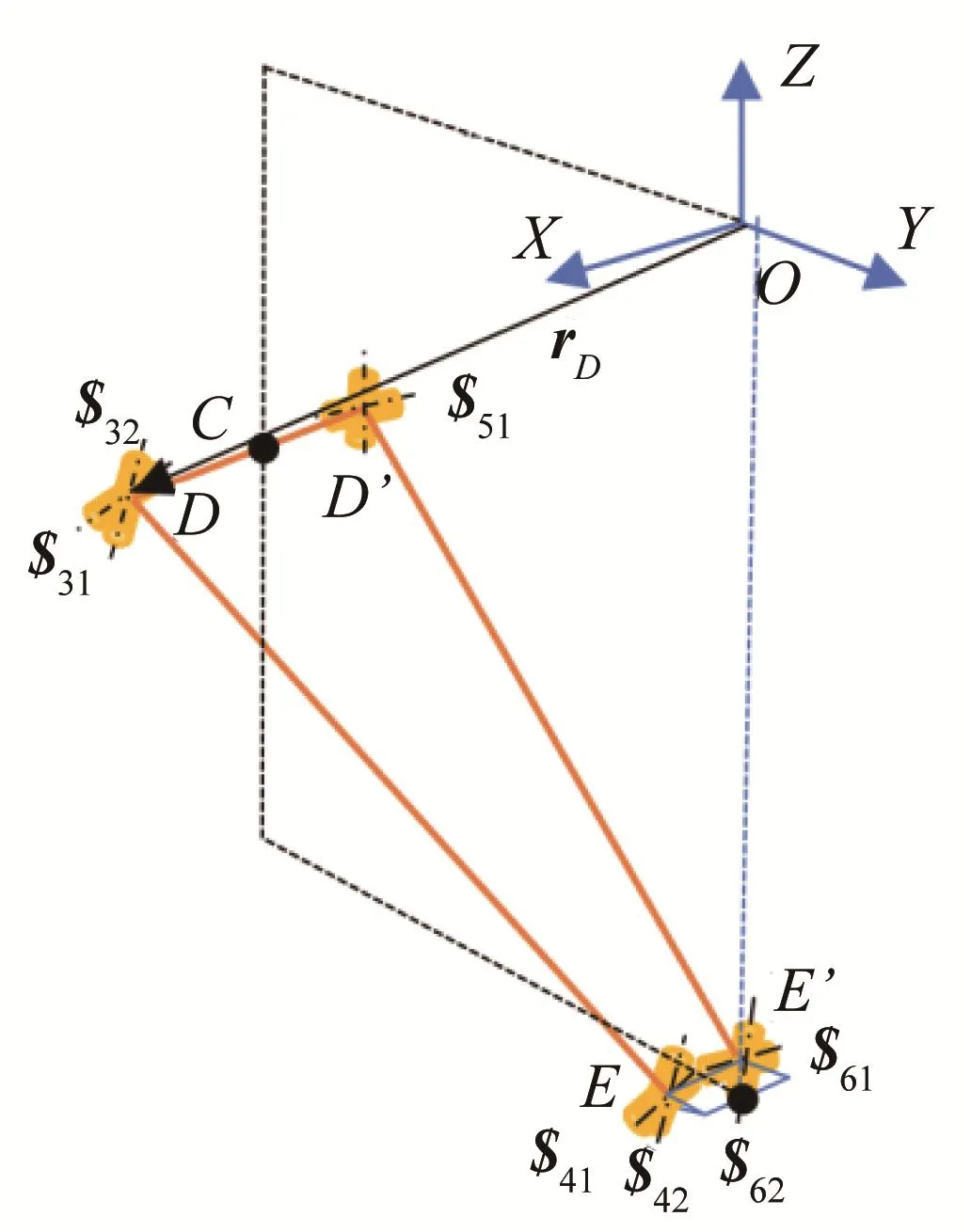
图4 4U闭环子链结构简图Fig.4 Structure diagram of 4U closed loop sub-chain

为便于分析，记DE分支中第1个U副的固定转轴的轴线矢量ω31=[ka1b10]（k=1，下同），摆动转轴的轴线矢量ω32=[ka2b2c2]，中心点D的位置向量rD=[kx^1y^1z^1]，由此可得第1个U副的运动旋量系为：

同理，记DE分支中第2个U副的固定转轴的轴线矢量ω41=ω31，摆动转轴的轴线矢量ω42=ω32，中心点E的位置向量则第2个U副的运动旋量系为：

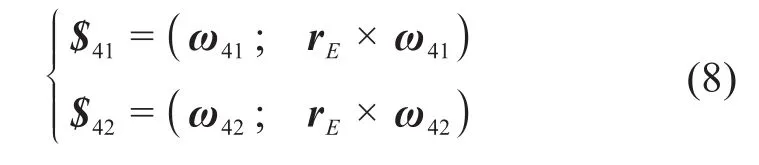
由此可得，DE分支的运动旋量系为：

根据旋量互易积概念，由式（9）求得DE分支的约束旋量系：

综上，可得到整个机器人机构中单条支链的运动旋量系：

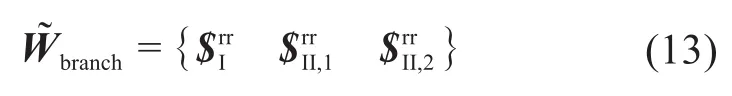
求解上述单条支链运动旋量系的反旋量，得到整个机器人机构单条支链的终端约束旋量系为：

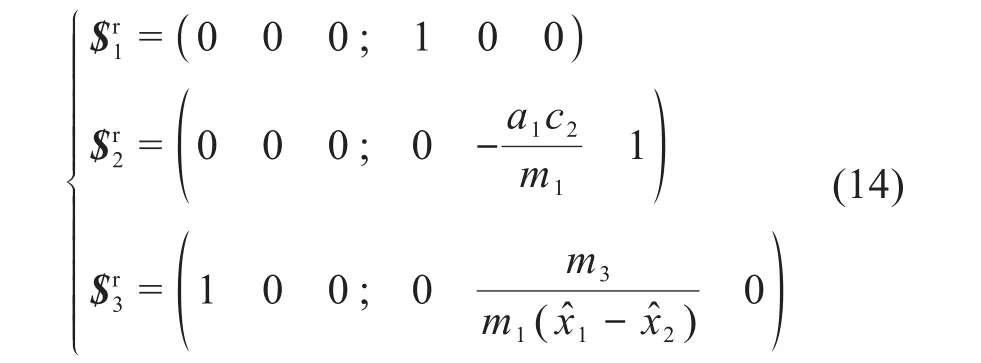
结合修正的G-K公式，对该机器人机构的自由度进行计算，其中考虑冗余约束的自由度M为：

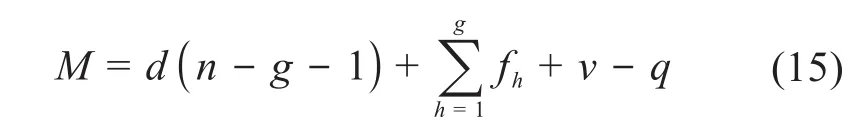
式中：d为机器人机构阶数，且d=6-λ，其中λ为机器人机构的公共约束数；n为机器人机构杆件数；g为机器人机构运动副数；fh为第h个运动副的自由度；ν为虚约束数；q为局部自由度。

综上所述，该机器人机构具有2个自由度，分别是沿Y、Z轴的平动。根据实际工程需求可知，该机器人能够满足提综臂旋铆加工过程中对零部件进行抓取和摆放的需求。同时，因该机器人机构的被动杆具有空间分布特征，其运动相互耦合，故其具有较大的X向刚度，能有效避免高速运动时的弹性变形。

2 辅助旋铆并联机器人机构运动学分析

为研究辅助旋铆并联机器人机构关节运动与末端位置的映射关系，对其进行运动学分析。如图5所示，基于惯性坐标系O-XYZ，设驱动杆与Y轴的夹角为θ，G点坐标为（0，y，z），i为支链序号，且约定当i=1时，sgn(i)=-1；当i=2时，sgn(i)=1，以单侧支链为例进行分析，其位置矢量可表示为：

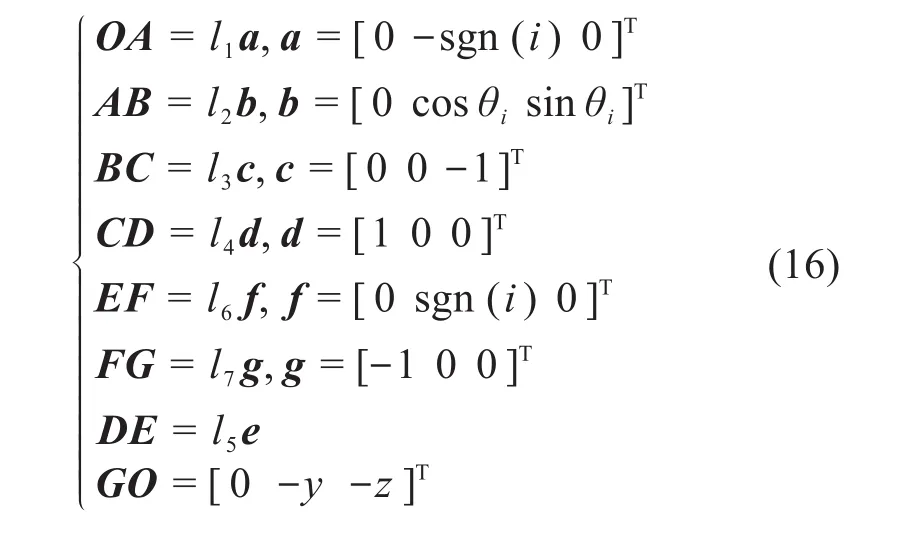
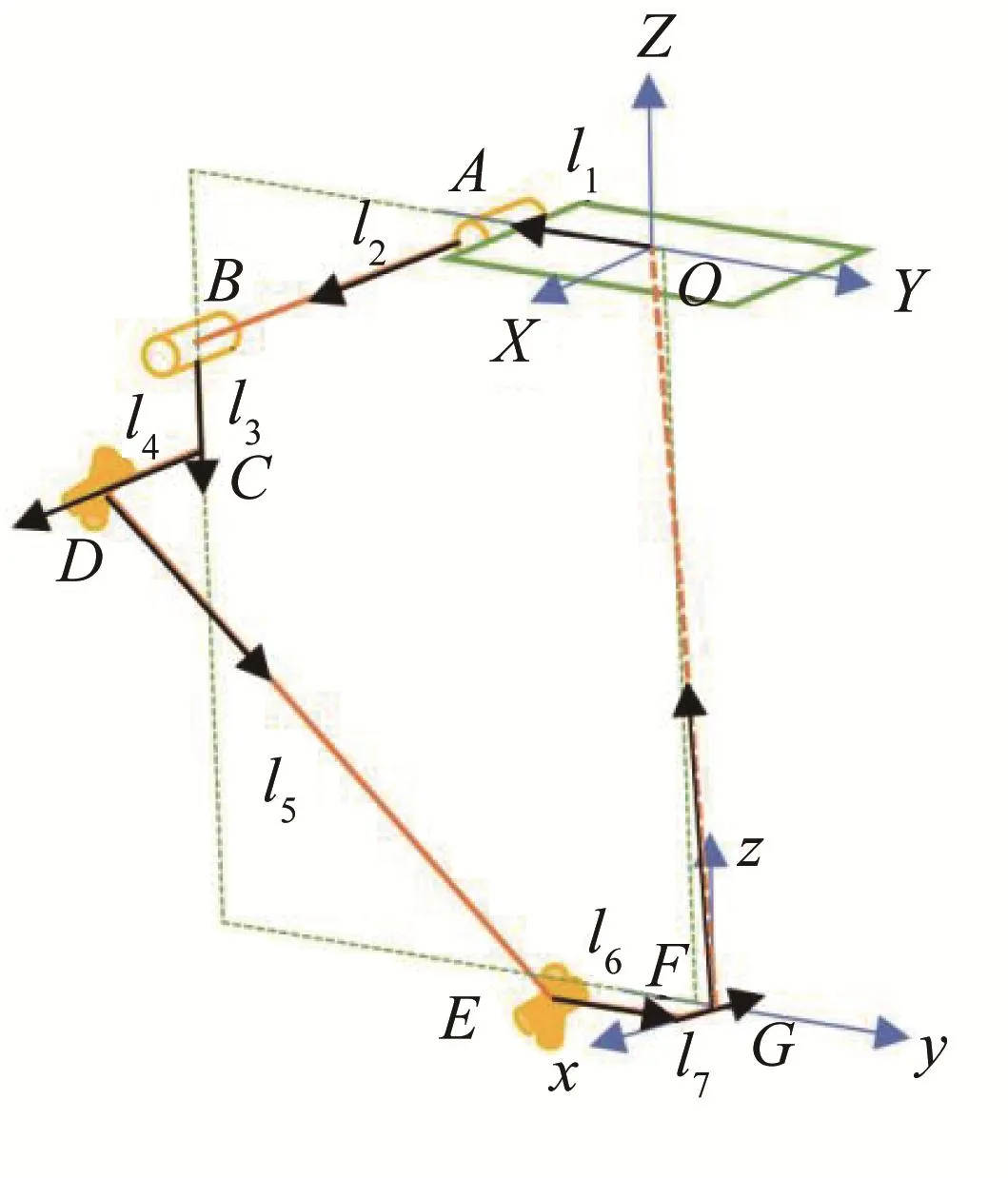
图5 辅助旋铆并联机器人机构单侧位置闭环矢量链Fig.5 Single position closed-loop vector chain of assisting-riveting parallel robot mechanism

根据闭环矢量法［17-19］，由图5可得如下闭环矢量方程：

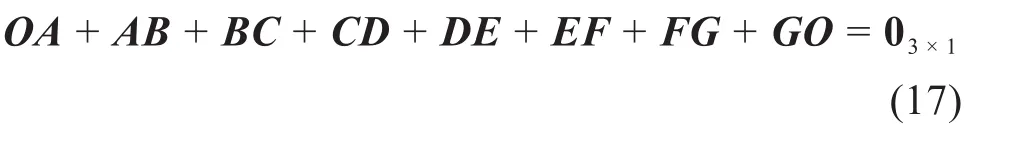
将机器人机构中所有杆件视为刚性杆，对向量DE求模，得到机器人的位置约束方程：

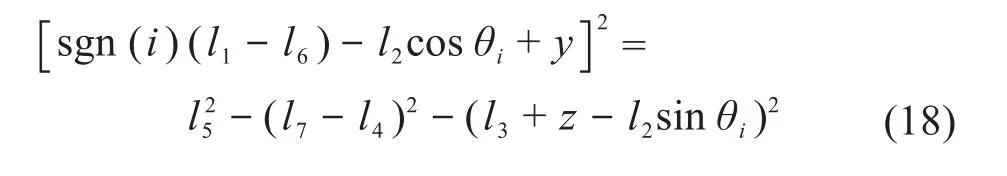
2.1 位置逆解推导

其中：

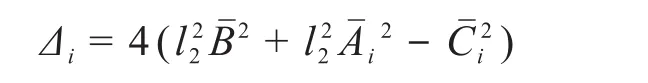
2.2 位置正解推导

位置正解对于并联机器人的控制具有重要意义，其通常借助数值迭代法（如牛顿法［20］）进行求解。但是，牛顿法对初始点选取的要求较高，若给定初始点与实际初始点偏离较大，则可能导致无法求得正确解，甚至无法收敛。考虑到该所设计机器人机构结构的特殊性，且其作平面运动（即存在解析正解），根据上文的约束方程，对该机器人机构进行运动学正向求解。

2.3 速度分析

对化简后的位置约束方程（19）关于时间求导，可得：

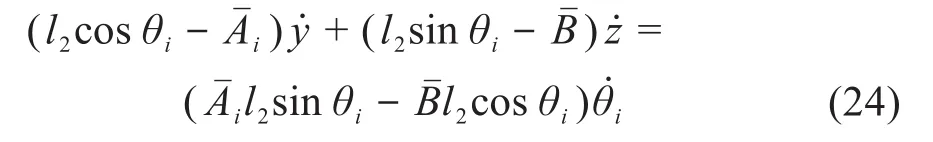
将式（24）整理成矩阵形式，可表示为：

式中：Jf为机器人机构的正向雅克比矩阵；Ji为机器人机构的逆向雅克比矩阵；为末端执行器参考点的速度；为驱动关节的角速度向量。

对式（25）作矩阵变换，可得该机器人机构的运动雅可比矩阵J：

联立式（26）至式（27）可得：

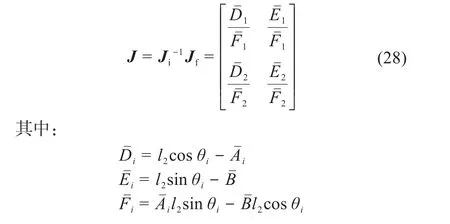
2.4 加速度分析

2.5 运行学正、逆解数值验证

为验证所推导的机器人机构运动学正、逆解的正确性，通过具体算例进行数值分析。首先设定辅助旋铆并联机器人末端执行器参考点的轨迹，并将其代入运动学逆解模型，求得驱动转角；然后将驱动转角代入运动学正解模型，求得末端执行器参考点的实际轨迹；最后通过对比末端执行器参考点的理论轨迹与实际轨迹来验证运动学正、逆解的正确性。不失一般性，现赋予辅助旋铆并联机器人一组尺度参数，如表1所示。表中：Hd为机器人驱动轴所在平面与任务工作空间中心的距离。

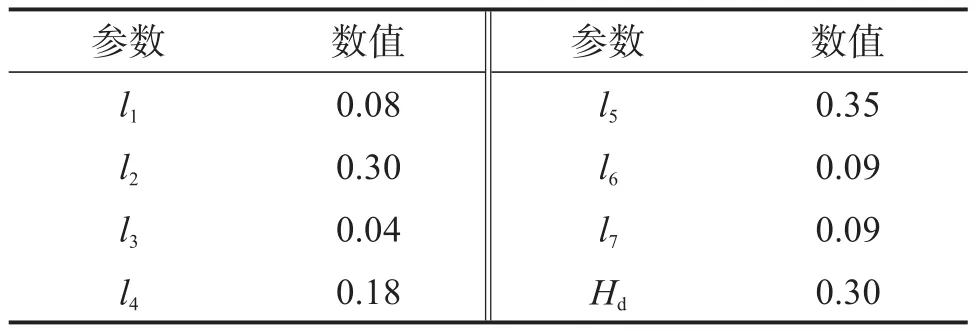
表1 辅助旋铆并联机器人的尺度参数Table 1 Dimensional parameters of assisting-riveting parallel robot 单位：m

令该机器人末端执行器参考点G的运动轨迹为半径等于0.1 m的圆形轨迹，通过数值计算得到其理论轨迹与实际轨迹的对比结果，如图6所示。定义位置误差为理论轨迹点与实际轨迹点的距离，由此可得位置误差的分布情况，如图7所示。

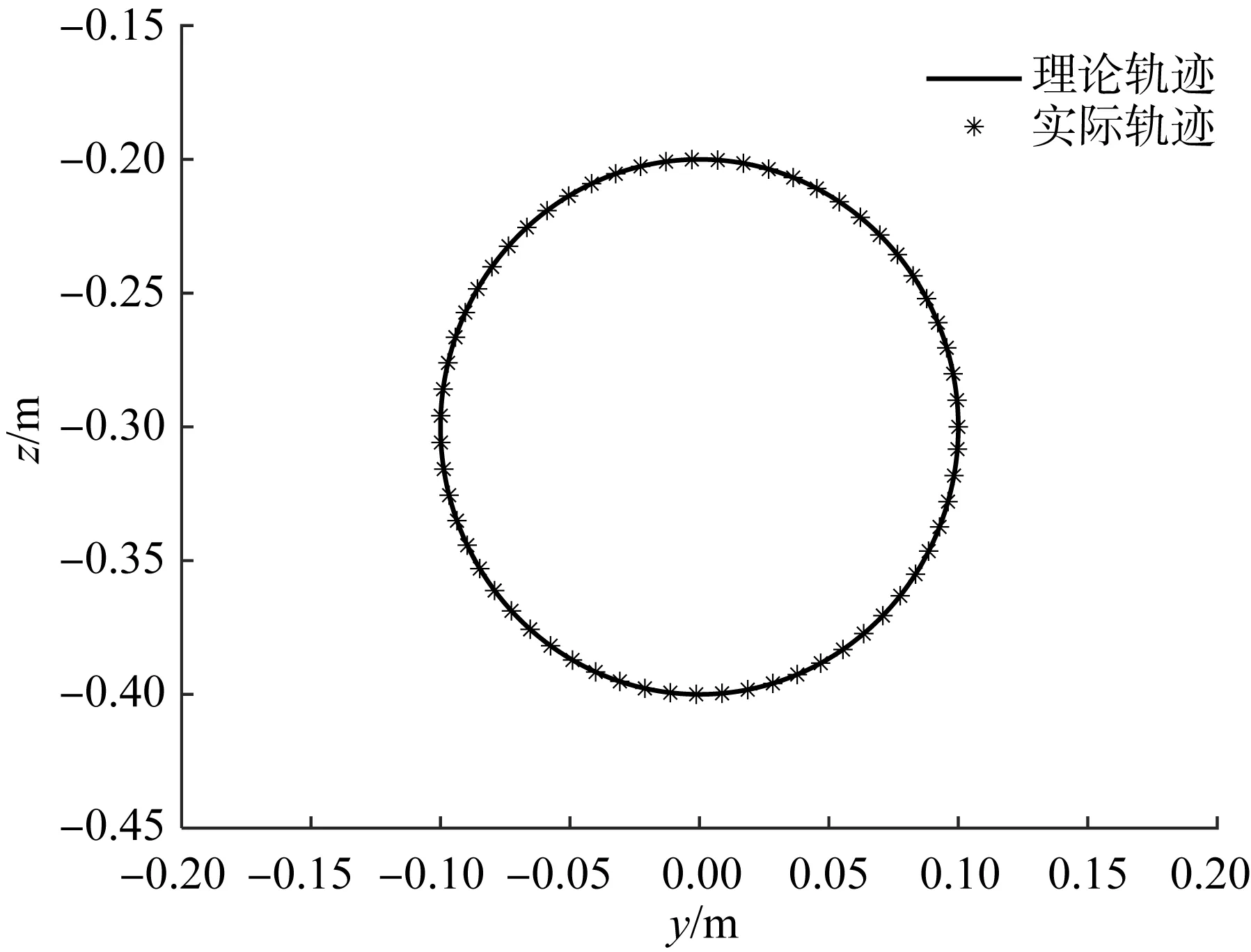
图6 辅助旋铆并联机器人末端执行器参考点的轨迹对比Fig.6 Comparison of trajectory of end effector reference point of assisting-riveting parallel robot

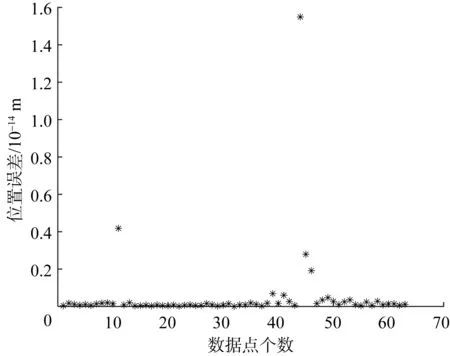
图7 辅助旋铆并联机器人末端执行器参考点的位置误差分布Fig.7 Position error distribution of end effector reference point of assisting-riveting parallel robot

综合图6和图7结果可知，基于上文推导的运动学正、逆解模型求得的辅助旋铆并联机器人末端执行器参考点的实际轨迹与理论轨迹的误差极小，近乎完全重合。由此说明，所推导的运动学正、逆解正确，可为后续的机器人高效运动控制研究奠定理论基础。

3 辅助旋铆并联机器人尺度综合与优化设计

3.1 任务工作空间与尺度设计变量

工作空间须根据生产线上传送带的宽度、运行轨迹中障碍物的高度等参数进行确定。在本文中，根据实际工程需求，设定辅助旋铆并联机器人的任务工作空间的宽度b=0.60 m，高度H=0.15 m的矩形区域，如图8所示。

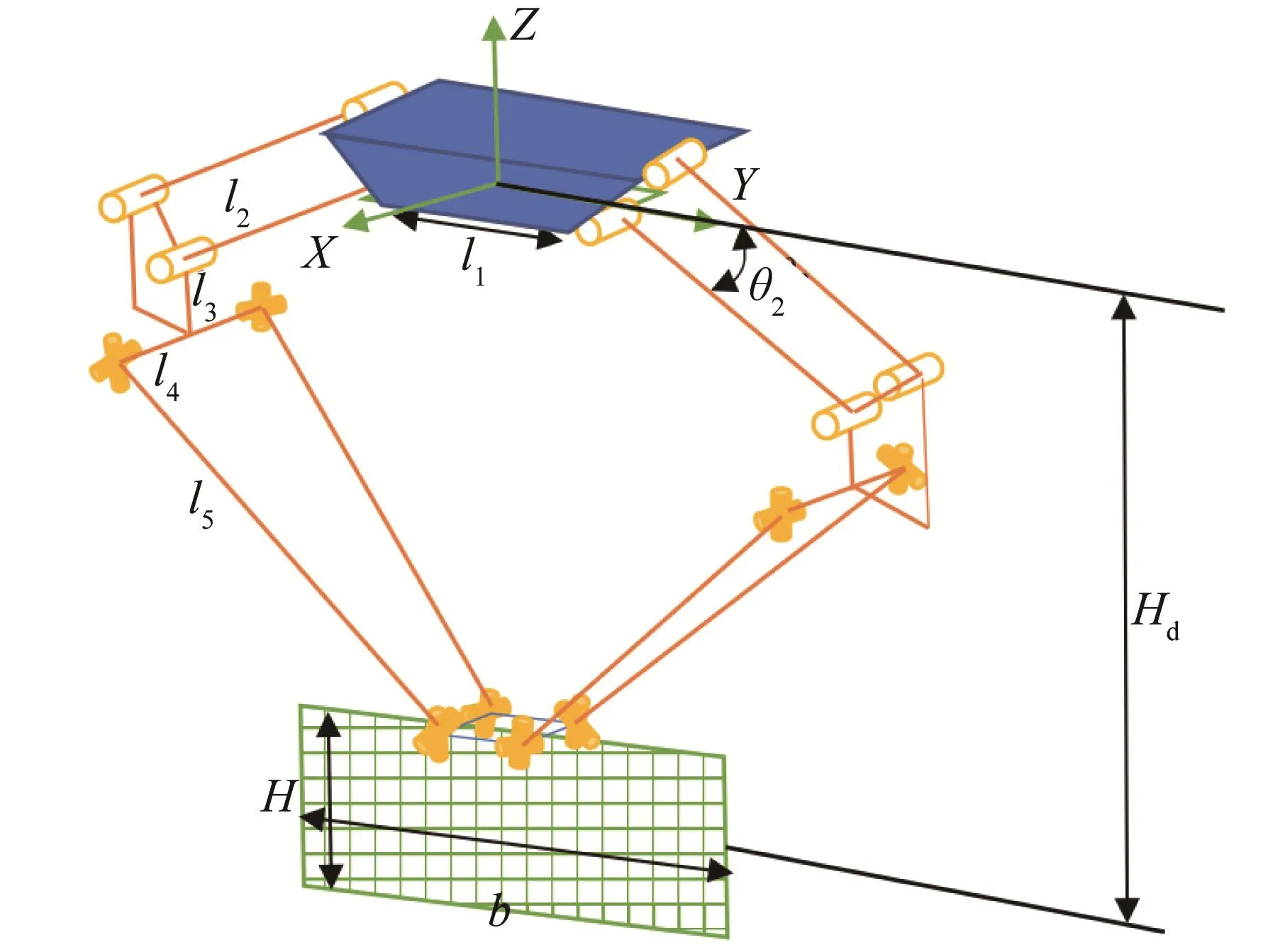
图8 辅助旋铆并联机器人的任务工作空间与尺度设计变量Fig.8 Task workspace and dimensional design variables of assisting-riveting parallel robot

考虑实际工程经验，并兼顾结构的紧凑性，设定机器人中间肘部连接架与主动臂相连接的转动副轴线与2个虎克铰中心连线的距离l3=0.07 m，虎克铰中心到YOZ平面的距离l4=0.09 m；为保证与动平台相连接的虎克铰的安装位置，设安装角为45°；设动平台尺寸l6=l7=0.06 m。由此可确定需要优化的尺度设计变量为l1、l2、l5和Hd。

3.2 运动性能评价指标

1）局域操作性能指标。

就工作空间与运动特性而言，运动雅可比矩阵J的条件数κ［5-6，21］是较为恰当的局域操作性能指标，其可表示为：

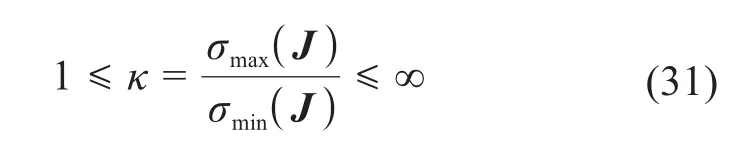
式中：σmax（J）和σmin（J）分别为运动雅可比矩阵的最大和非零最小奇异值。

2）全域操作性能指标。

考虑到κ会随机构的位形变化而变化，采用类似Gosselin和Angeles［22］提出的条件数全域均值作为全域操作性能指标，表示为：

式中：W为机器人任务工作空间的体积。

3）全域波动量指标。

由于全域雅可比矩阵条件数均值并不能完整地描述机构的全域操作性能，故构造一个条件数波动量指标，以反映条件数在全域的波动程度，表示为：

式中：κmax和κmin分别为运动雅可比矩阵条件数的全域最大值和最小值。

4）全域综合性能指标。

考虑运动雅可比矩阵条件数全域均值及其波动量的影响，构造全域综合性能指标，表示为：

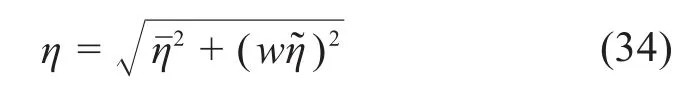
式中：w为权重系数，一般情况下取w=1。

3.3 约束条件分析

3.3.1 转角约束

1）驱动转角。

由式（20）可知，当Δi≤0时，驱动转角会出现复数解，但该解无意义。故若要保证驱动转角存在实数解，需对Δi进行约束，即驱动转角存在实数解的条件为：

鉴于机器人采用平行四连杆机构驱动，为防止平行四连杆机构出现杆件干涉，故驱动转角的约束条件为：

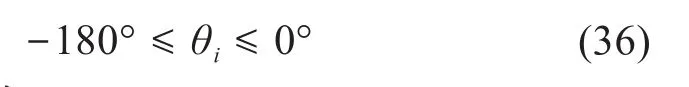
2）虎克铰转角。

虎克铰有2个自由度，分别为绕2个转轴的回转，考虑到其运动与结构具有对称性，以其中一组为例进行分析。

在图5中，记DE的单位方向向量为e，转动关节轴线ζ6的单位方向向量由此可得，转动关节轴线ζ5的单位方向向量e2=e1×e；XOY平面的单位法向量；DE与转动关节轴线ζ5所在平面的法向量e4=e×e2。

故绕转动关节轴线ζ6的转角（即被动杆DE与XOY平面的夹角）φ1=arccos＜e2，e3＞；绕转动关节轴线ζ5的转角φ2=arccos＜e1，e4＞。

为防止虎克铰中十字轴连接的两杆发生干涉，对其2个转角进行约束，即有：

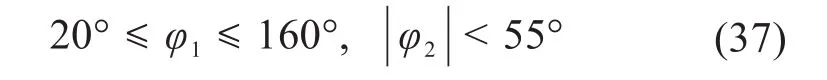
3）传动性能。

在工作空间中，当条件数κ=1时，机器人机构仍可能存在奇异位形，故须考虑其传动性能。假设向量DE在YOZ平面的投影为DEYZ，与平面5R机构相类似［5，9］，现考虑采用向量AB与向量DEYZ的夹角μ（锐角）来描述该机器人机构的传动性能［5］，即：

为获得良好的传动性能，μ的最小值应大于许用值[μ]。根据实际工程经验，一般取[μ]=35°～40°。

3.3.2 体积约束

为保证机器人机构整体结构紧凑，防止其体积过大，对其杆长进行约束，表示为：

一般情况下，取λt=1～1.2［5］。

3.4 尺度综合模型建立

基于上述分析，将全域综合性能指标η（其是关于设计变量的函数）作为尺度综合的目标函数；约束条件包括各驱动转角约束、传动性能约束以及尺度设计变量的取值约束。因此，辅助旋铆并联机器人的尺度综合问题可归结为：在给定的任务工作空间内满足上述约束条件的基础上，使得机器人机构的全域操作性能实现最优的非线性规划问题。构建的尺度综合模型如下：

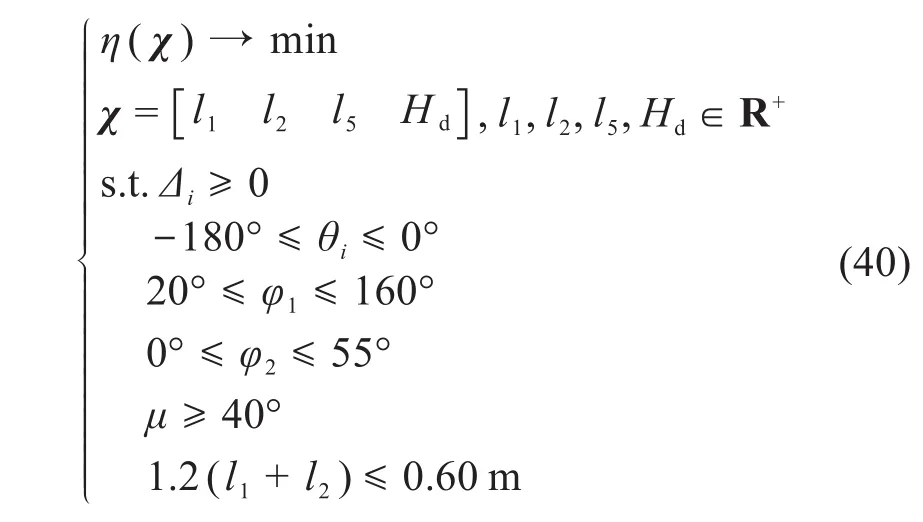
辅助旋铆并联机器人尺度设计变量的取值范围如表2所示。

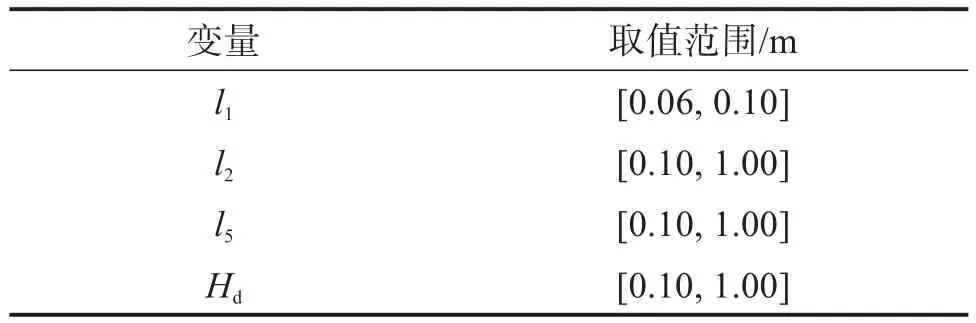
表2 辅助旋铆并联机器人尺度设计变量取值范围Table 2 Value range of dimensional design variables of assisting-riveting parallel robot

3.5 PSO算法介绍

根据尺度综合，可得到一个单目标且存在多个非线性约束的优化模型。为实现全局寻优，本文采用PSO算法［6，11］来筛选可行域内的最优解。PSO算法与GA类似，是一种基于迭代的智能优化算法，其从随机解出发，通过迭代寻找最优解。在PSO算法中，每一个优化问题的解被称为“粒子”，用优化函数决定的适应度来描述每个粒子距离目标点的位置关系，用速度矢量表示每个粒子向目标点趋近的速度和方向。在可行域中粒子通过跟随当前时刻的最优粒子进行搜索和逼近，最终获得全局最优解。PSO算法具有易实现、精度高和收敛快等优点，其具体流程如图9所示。

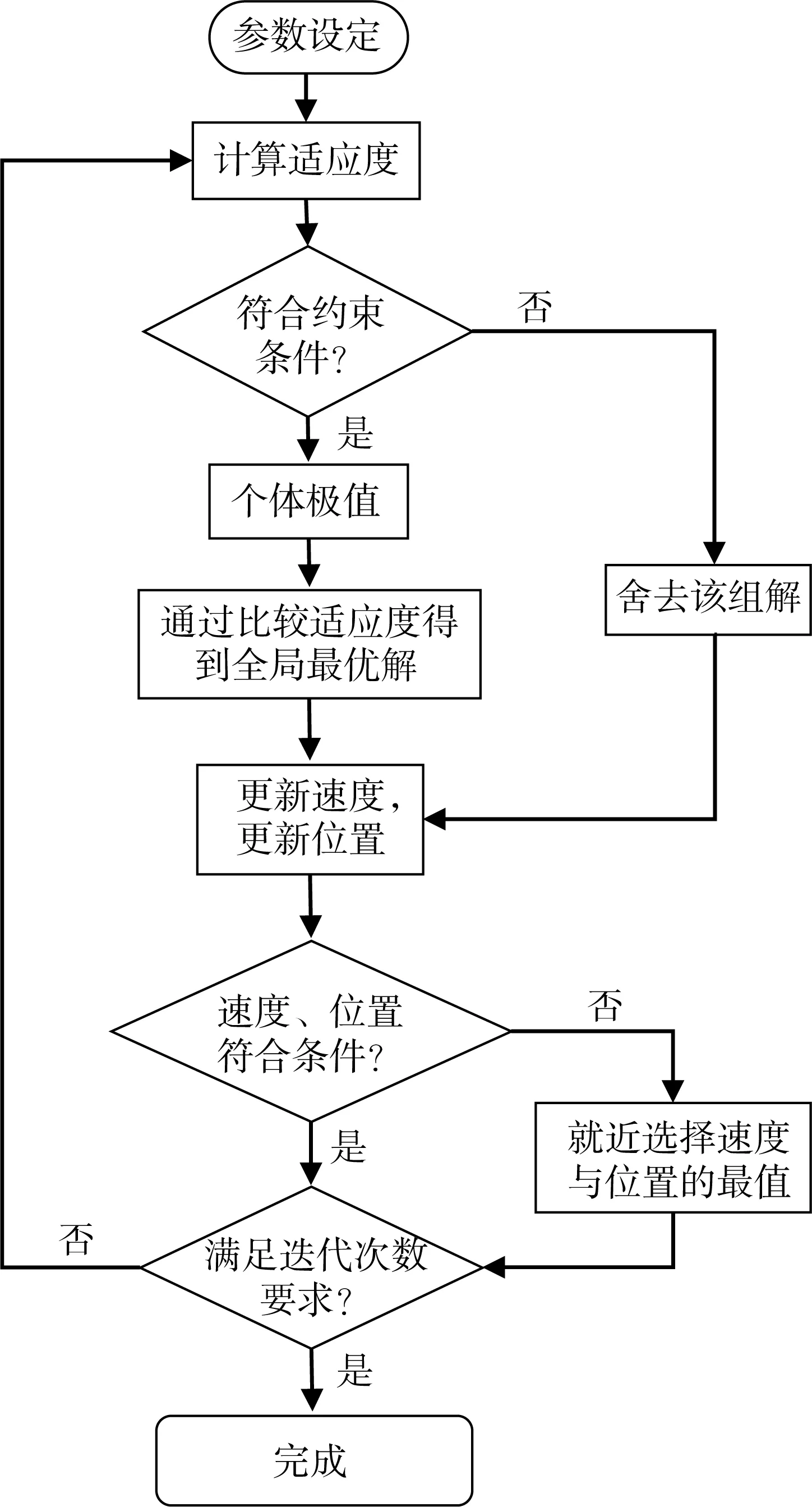
图9 PSO算法流程Fig.9 Flow of PSO algorithm

随机粒子通过搜索2个“最优解”来调整自身的搜索方向和行进速度，从而完成粒子个体和粒子群体的寻优过程。2个“最优解”分别为：1）当前单个粒子通过搜索获得其最优解，称为个体极值pbest；2）从整个粒子群中所有个体最优解中搜索获得的全局最优解，称为全局极值gbest。PSO算法的基本迭代过程如下：

式中：为粒子速度；为粒子位置；为惯性权重，一般取0.4～0.8；、为学习因子，一般取1.8～2.0；rand为［0，1］内的随机数。

3.6 优化结果分析

参考以往经验［6］，本文取取种群个体数为500，迭代次数为500。基于PSO算法的辅助旋铆并联机器人尺度综合迭代过程如图10所示。由图10可知，当迭代到160次时，优化目标值趋于平稳，到达最优解附近；在迭代267次后，优化目标值几乎不再发生变化，即到达最优解。整个迭代过程收敛速度良好，精度较高，可以实现全局寻优。最终得到的优化结果如表3所示。其中，优化后机器人机构的全域综合性能指标η=1.678 5（η越接近1表明机器人的综合性能越好）。

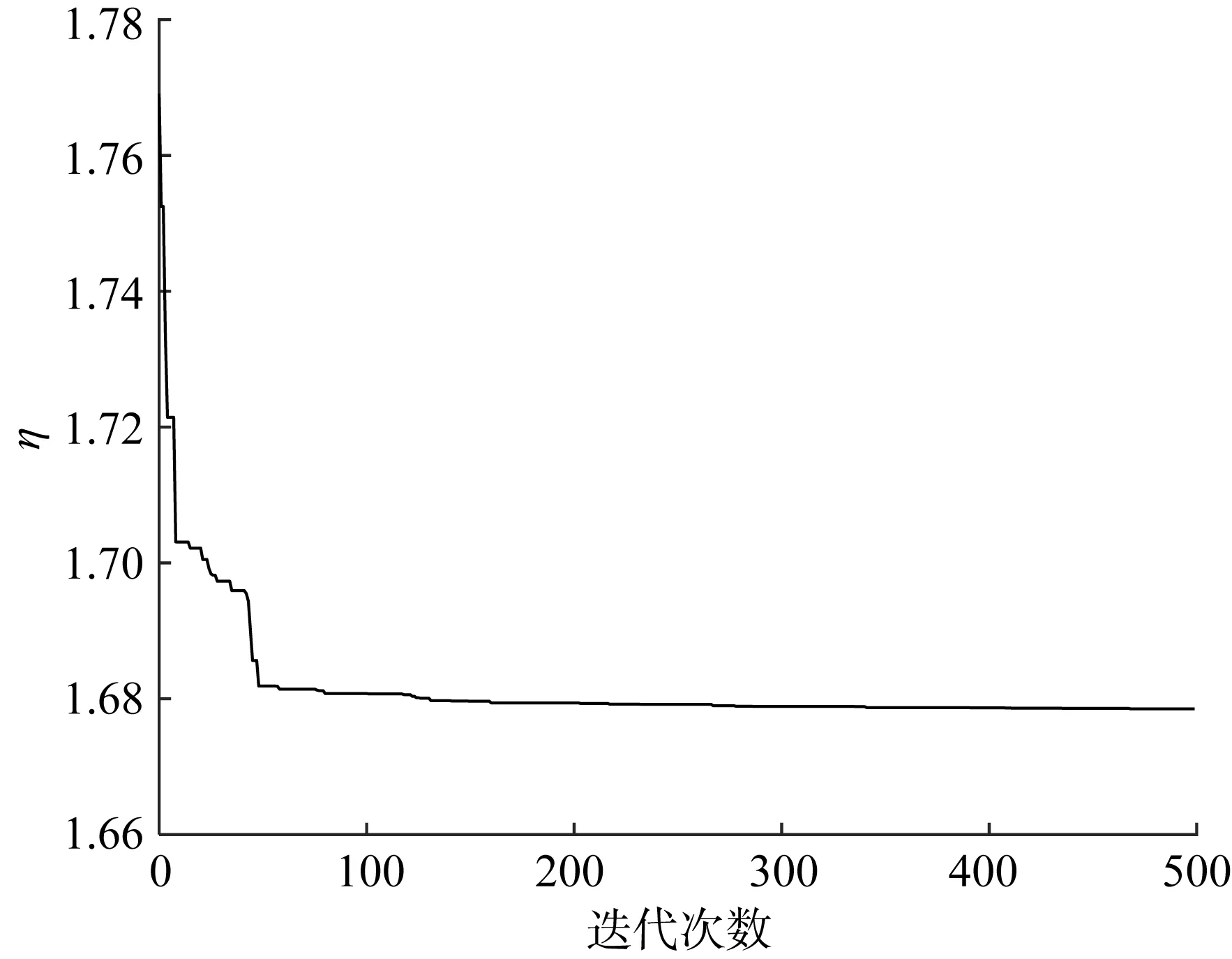
图10 基于PSO算法的辅助旋铆并联机器人尺度综合迭代过程Fig.10 Dimensional synthesis iterative process of assistingriveting parallel robot based on PSO algorithm

表3 辅助旋铆并联机器人尺度参数优化结果Table 3 Optimization results of dimensional parameters of assisting-riveting parallel robot

根据相关运动性能指标的定义，代入优化结果后得到条件数在机器人任务工作空间内的分布情况，如图11和图12所示。由图可知，条件数在整个任务工作空间的分布比较均匀，其极大值为1.25，且分布在矩形工作域Z向的最近端与最远端；最大条件数与最小条件数的比值较小。由此可以判断，在此条件下，该机器人机构的全域运动性能波动平缓，验证了优化设计结果的有效性。

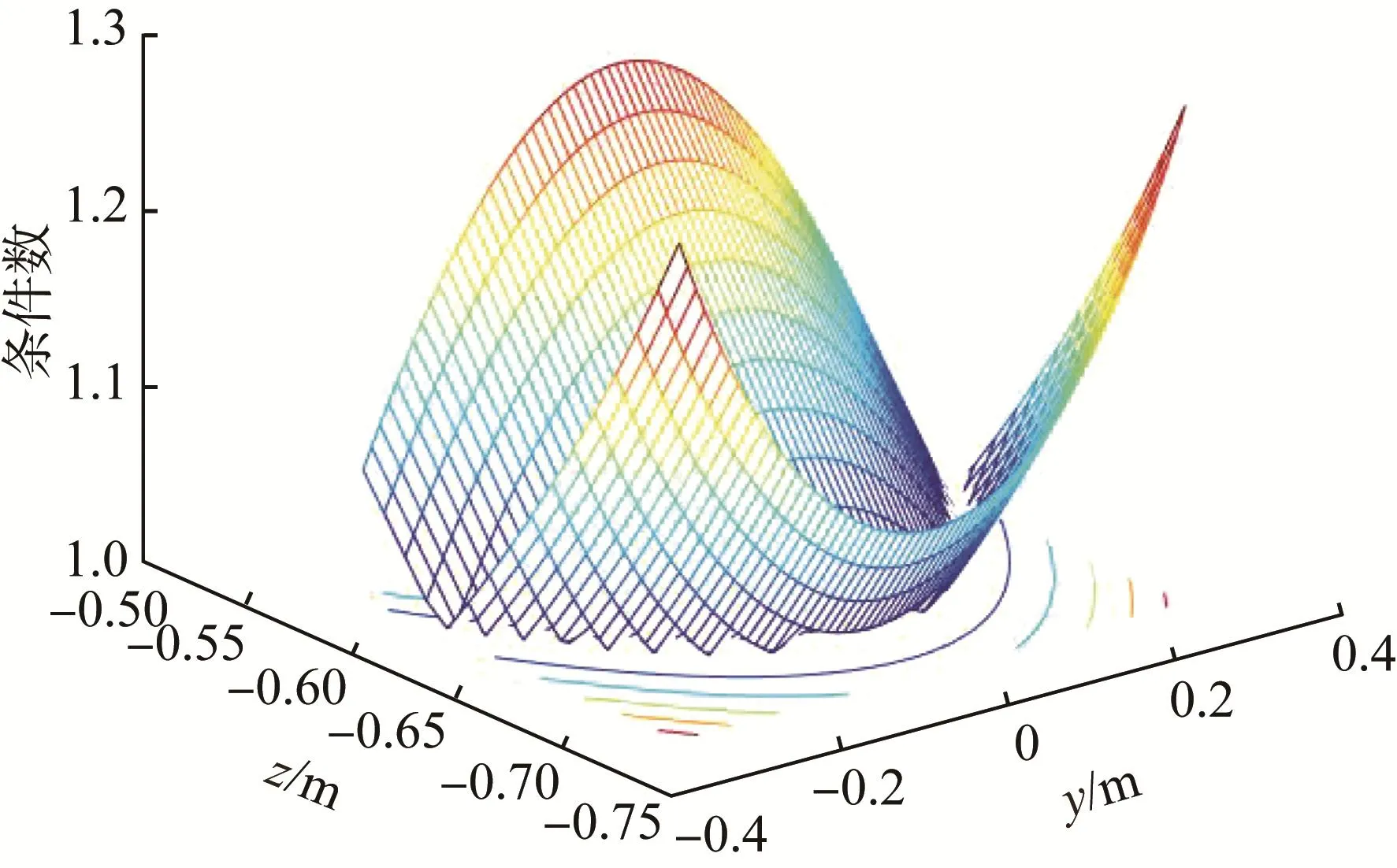
图11 条件数在辅助旋铆并联机器人任务工作空间内的三维分布Fig.11 Three-dimensional distribution of condition number in task workspace of assisting-riveting parallel robot

图12 条件数在辅助旋铆并联机器人任务工作空间内的二维分布Fig.12 Two-dimensional distribution of condition number in task workspace of assisting-riveting parallel robot

根据尺度综合结果，借助SolidWorks三维设计软件构建辅助旋铆并联机器人的整体虚拟样机模型，如图13所示。其中，为使机器人的工作性能更优，将机器人本体（执行机构）与横移机构（滚珠丝杆机构）相结合，以在实现Y、Z方向二维平动的同时，满足X向大范围进给运动的需求，进一步扩大机器人的实际工作范围。

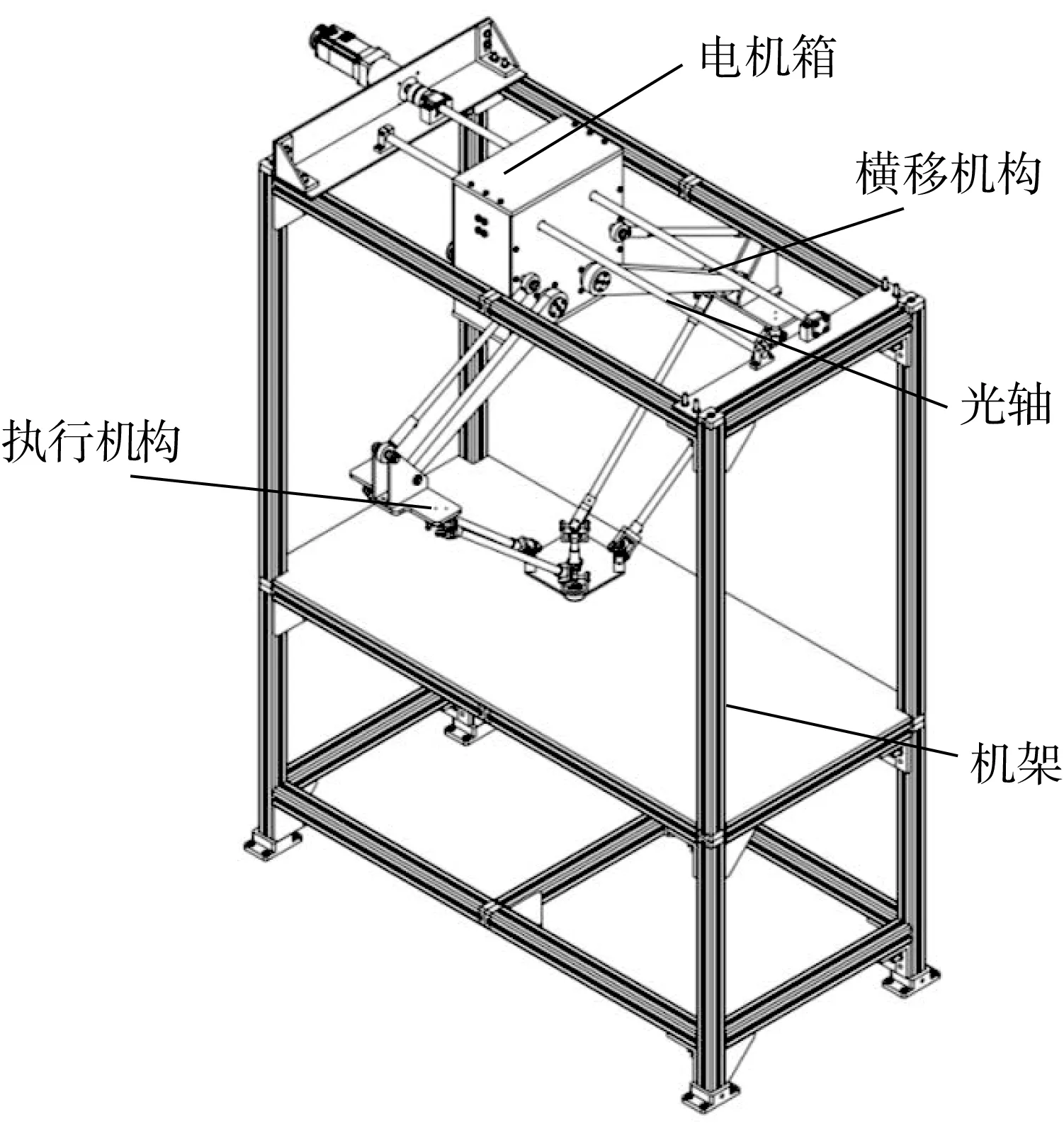
图13 辅助旋铆并联机器人整体虚拟样机模型Fig.13 Overall virtual prototype model of assisting-riveting parallel robot

4 基于ADAMS的辅助旋铆并联机器人运动仿真

为验证运动学理论分析和优化设计结果的正确性，以及降低样机开发成本，借助ADAMS软件对优化后的辅助旋铆并联机器人虚拟样机模型开展多体运动仿真。根据提综臂旋铆加工对零部件抓取和摆放的需求，拟选用“门”字形轨迹作为所设计机器人末端执行器参考点的运动轨迹，并分别采用以正弦函数为修正函数的改进梯形加速度运动规律［23］对Y、Z方向的运动进行控制，以避免起、止时刻的加速度突变引起的冲击，取最大加速度 amax＝3g（g=9.81 m/s2）。为便于进行多体运动仿真，对机器人执行机构的运动关节作适当简化。将简化后的机器人机构虚拟样机模型导入ADAMS软件，并对机器人机构的关节约束和驱动进行定义，建立其多体运动仿真模型，如图14所示。

图14 辅助旋铆并联机器人机构的ADAMS多体运动仿真模型Fig.14 ADAMS multi-body motion simulation model of assisting-riveting parallel robot mechanism

根据规划的机器人末端执行器参考点的运动规律，借助MATLAB软件求得其驱动关节的运动规律。在ADAMS多体运动仿真模型中，对机器人驱动臂施加电机驱动，则电机的运动规律即为所求驱动关节的运动规律。通过虚拟传感器对机器人末端执行器参考点的位置进行测量，由此得到位移、速度以及加速度的变化曲线仿真结果，并与理想结果进行对比，分别如图15至图17所示。

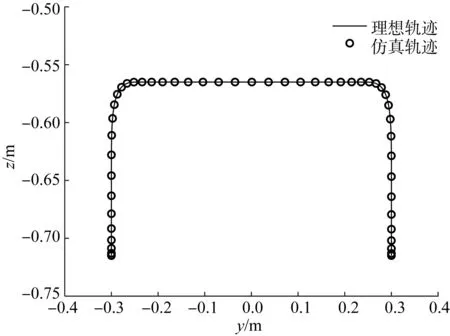
图15 辅助旋铆并联机器人末端执行器参考点的理想轨迹与仿真轨迹对比Fig.15 Comparison of ideal trajectory and simulated trajectory of end effector reference point of assisting-riveting parallel robot

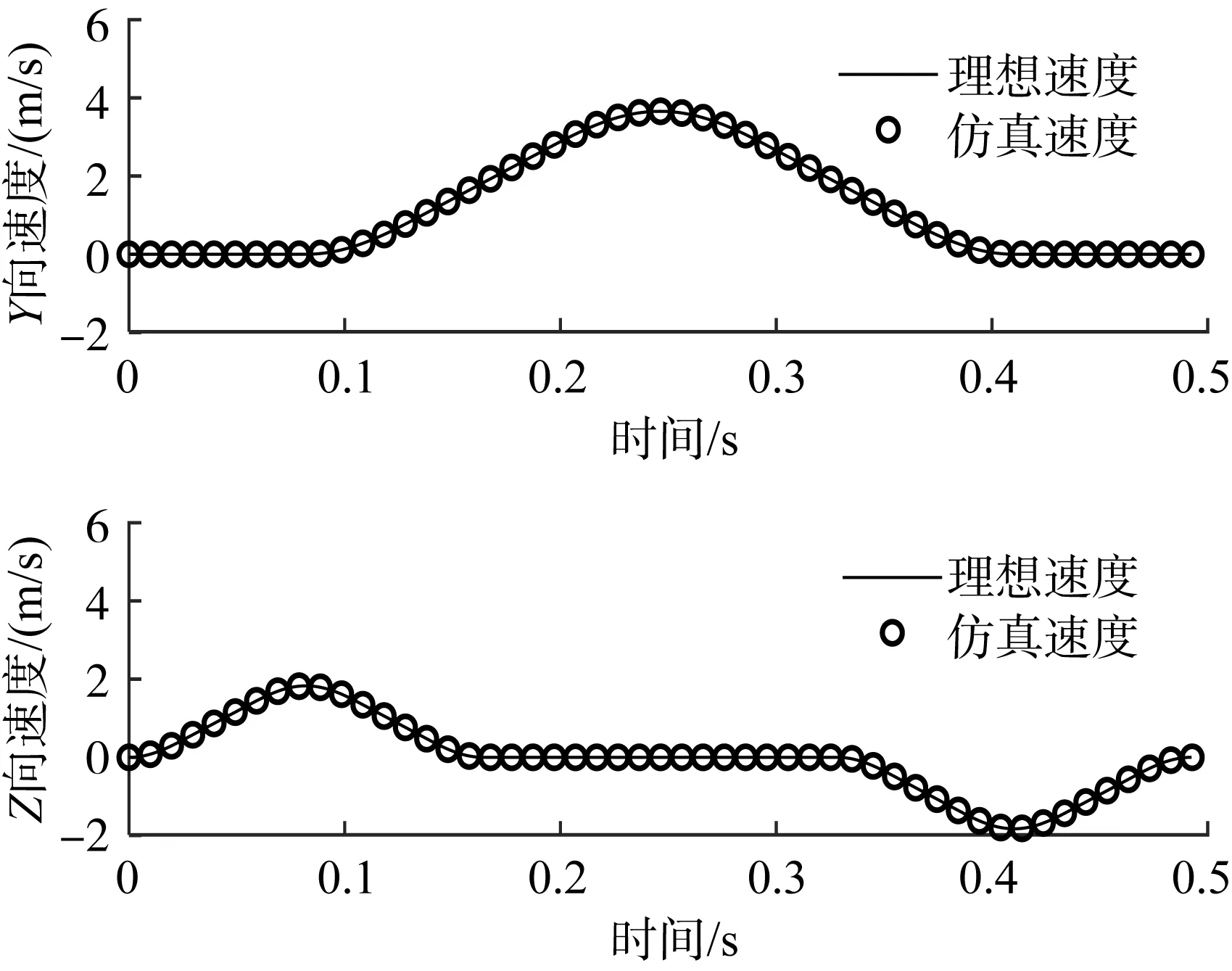
图16 辅助旋铆并联机器人末端执行器参考点的理想速度与仿真速度对比Fig.16 Comparison of ideal speed and simulated speed of end effector reference point of assisting-riveting parallel robot

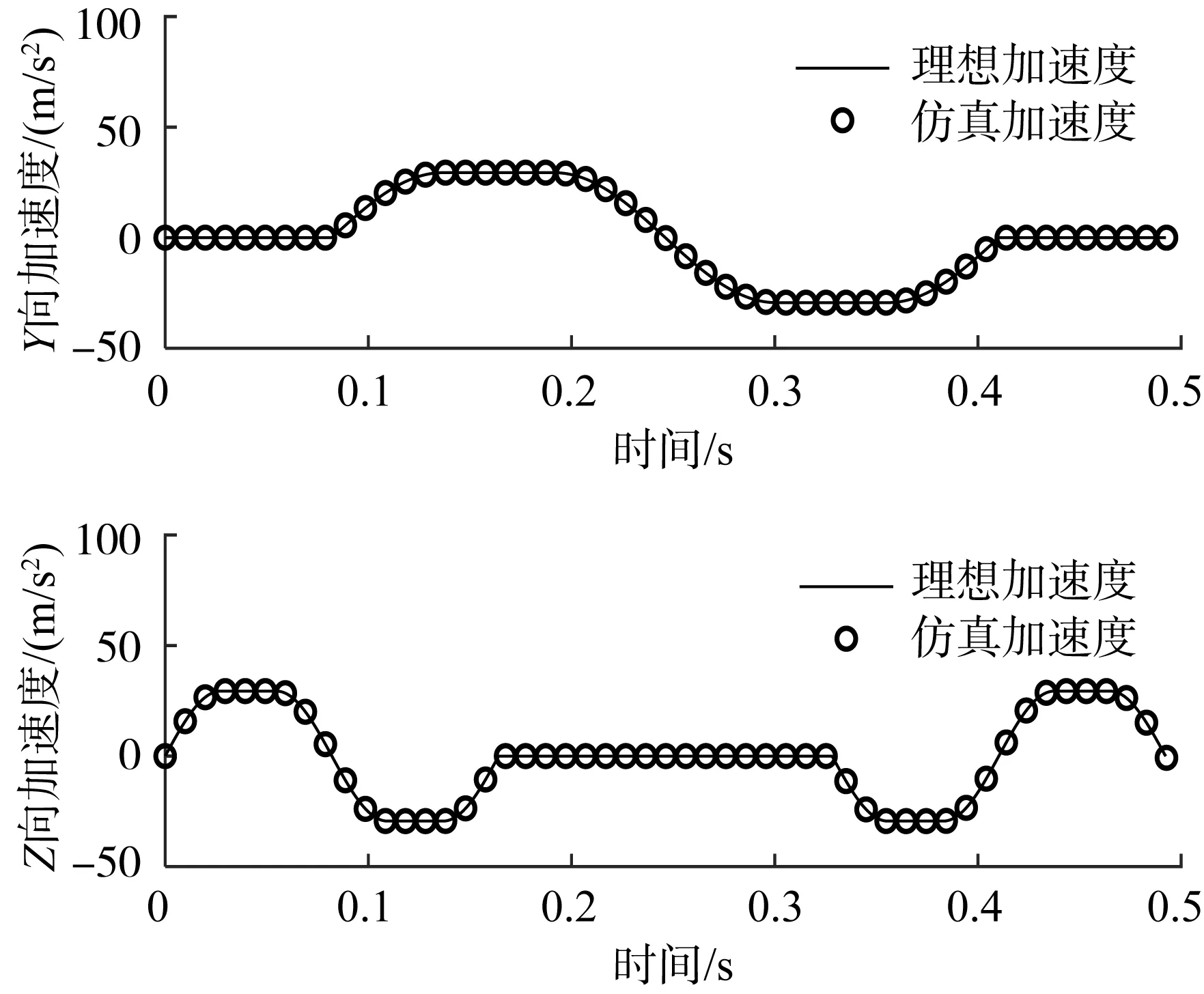
图17 辅助旋铆并联机器人末端执行器参考点的理想加速度与仿真加速度对比Fig.17 Comparison of ideal acceleration and simulated acceleration of end effector reference point of assisting-riveting parallel robot

从图中可以看出，辅助旋铆并联机器人末端执行器参考点的轨迹、速度仿真曲线与其理想曲线的重合度高；加速度曲线的变化平缓，且在起、止时刻的加速度均为0 m/s2（无突变），无刚/柔性冲击。需要指出的是，由于ADAMS多体运动仿真模型考虑了摩擦等因素，使得加速度仿真曲线在理想曲线上下轻微波动。综上可知，运动学理论分析及优化结果正确可靠，可为后续的机器人实体样机制造及其高效运动控制奠定基础。