基于缓冲阻尼的空间大惯量负载驱动系统的研究
2022-03-10杨新海沈晓鹏赵继亮苑会领
杨新海,沈晓鹏,赵继亮,谢 哲,苑会领
(1.上海宇航系统工程研究所,上海 201109;2.上海市空间飞行器机构重点实验室,上海 201109)
由于空间失重效应,飞行器在轨工作时的负载对象大部分为惯性负载。转动惯量是惯性负载的主要形式,较大的转动惯量达到104~106kg·m2。例如:在空间站组装过程中,飞行器舱体须进行转动[1-3],则舱体的转动惯量达到 106kg·m2[4],较之于地面的大惯量负载高出几个数量级,如一般测控雷达的转动惯量仅为 103kg·m2[5]。超大的转动惯量要求舱体转位机械臂的驱动关节具有较强的负载驱动和制动能力[6]。地面工程机械所采用的液压伺服系统虽然可以实现超大惯量负载的驱动[7-8],但其存在功耗和质量过大、空间环境适应性差等问题,不适用于空间飞行器。若采用电机直驱的方式来实现大惯量负载平稳且精确的运动控制,则需要一个超大功率的电机,且必须具有能与大负载惯量相匹配的转子转动惯量[9-10],这与空间机构对驱动系统功率和质量的严格限制相矛盾。文献[11]提出了一种基于全闭环+模糊自适应PID(proportion-integration-differentiation,比例-积分-微分)的控制方法,利用伺服电机实现了大惯量转台系统较高的响应速度和控制精度,但该控制方法相对复杂,工程应用的可靠性不够高,且所研究对象的转动惯量依然较小,对于超大惯量负载驱动的工程可复制性有待验证。利用现有较为成熟的技术只能实现负载转动惯量仅为电机转动惯量几倍的电机调速控制[12-14]。
此外,由于缺少辅助机构如齿轮、带轮等的传动,电机直驱方式会在不确定条件因素下对驱动系统带来伺服控制的波动,包括力矩纹波、参数变化、外部扰动、自身非线性和无法模型化的动力学特性[15-17]。
增大驱动系统的机械减速比固然可以降低电机端的等效负载惯量,然而超大的减速比会严重影响驱动机构的效率和系统频响特性,这对需要在地面快速作业的机器人来说是致命的缺点。相反,不同于地面机械装置如工业机器人,空间飞行器不需要较优的频响特性,但在功耗和质量方面受到严格限制。为了保证飞行器的安全和稳定,可以采用以小功率驱动大负载即以时间换能量的方式,通过延长启动时间和制动时间实现较为平稳的启动和制动。
缓冲阻尼技术已经广泛应用于航天器的研制中。如可控阻尼器已经成功用于空间交会对接机构[18-19],在飞行器对接缓冲过程中,起到了关键的惯性动能缓冲和消耗的作用。基于该技术的应用背景,笔者以空间站组装过程中转位的舱体为研究对象,应用空间飞行器机构的缓冲阻尼技术,建立具有多级齿轮传动、弹簧缓冲、阻尼器耗能及电磁制动等功能的驱动系统,以实现在空间站实验舱舱体转位过程中超大惯性负载的平稳驱动和精确制动。
1 大惯性负载驱动系统的模型
1.1 驱动原理
驱动机构传动链分为驱动主路、驱动支路、缓冲支路和耗能支路四部分,如图1所示。驱动主路和驱动支路构成驱动基本传动链路,驱动主路并联于缓冲支路和耗能支路,实现集成缓冲阻尼功能。驱动支路包含驱动电机和减速器。驱动主路与各支路之间通过齿轮传动连接和传递载荷。
1.2 参数设计
根据平稳启动的特性要求来确定总传动比。首先根据驱动机构制动时的负载惯量和阻尼衰减的振动幅值确定驱动机构的缓冲阻尼参数,然后确定各组件之间的传动比分配关系。在空间站组装过程中,舱体转位运动总转动惯量为2.2×106kg·m2,据此选定空间交会对接机构使用的J36直流无刷电机、弹簧机构和电磁阻尼器,采用双电机驱动、双阻尼器耗能的工作模式。要求启动过程运行平稳,制动振幅小,且缓冲衰减快。
1.2.1 总传动比的确定
驱动机构各组件之间的传动比关系如图2所示。其中i1、i2、i3分别为电机到弹簧机构、弹簧机构到末端输出、弹簧机构到阻尼器的传动比。
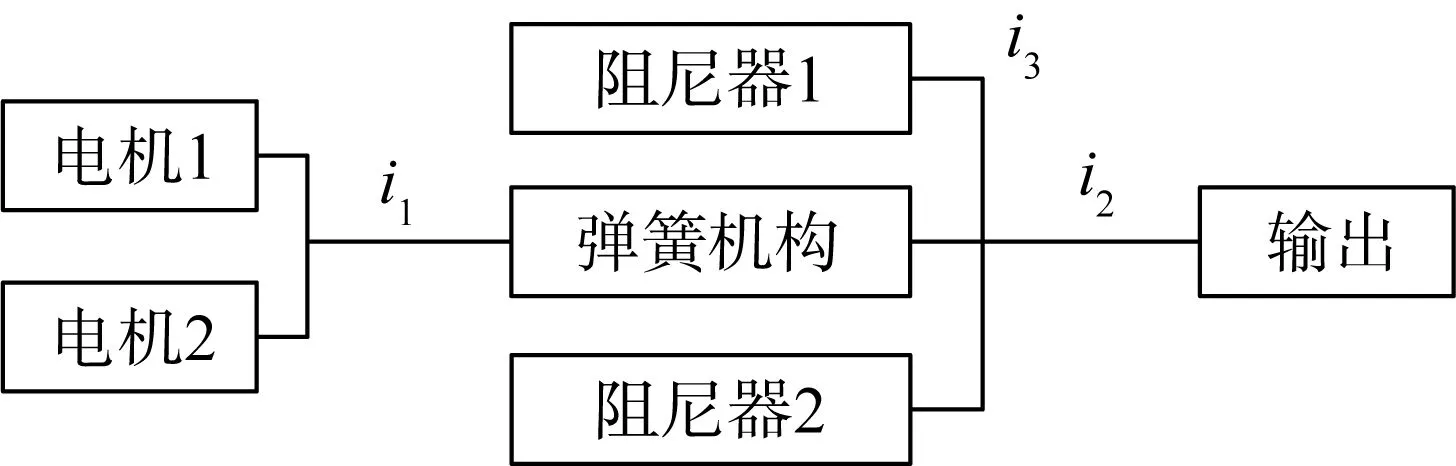
图2 驱动机构各组件之间的传动比关系Fig.2 Transmission ratio relationship between components of driving mechanism
由电机启动时间的经验公式分析启动扭矩、转动惯量和启动阻力矩之间的关系:
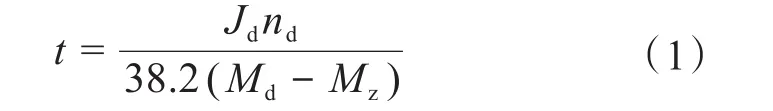
式中:t为电机转子的启动时间,s;Jd为电机转子端等效转动惯量,kg·m2,Jd=J/i,J为输出端转动惯量,i为总传动比;nd为电机额定转速,r/min;Md为电机额定力矩,Mz为启动阻力矩,N·m。
由于Mz≪Md,可予以忽略,则在双电机工作模式下,有:
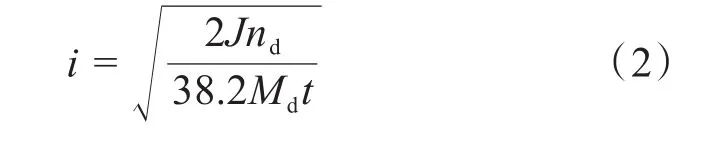
已知J=2.2×106kg·m2,nd=2150r/min,Md=0.035N·m,要求启动时间 t≤0.2 s,求得i≥233 826,可取值为235 000。考虑到电机空载转速较额定转速高30%,则驱动机构的角速度ωmax≈0.14°/s。
1.2.2 等效刚度和等效阻尼系数的设计
带缓冲阻尼特性的驱动机构的传动链结构复杂,传动空程、传动效率、摩擦阻尼、弹簧回滞特性等非线性因素对驱动机构运动特性的综合影响无法用准确的数学模型来描述。因此,用等效刚度和等效阻尼来系统描述机构的运动特性。
1)等效刚度。
弹簧机构的特性曲线如图3所示,驱动机构的等效刚度特性曲线如图4所示。其中:k为驱动机构回转结构的等效传动刚度,包括弹簧机构本身的结构刚度和齿轮传动链刚度折算到末端的等效刚度;k1为驱动机构回转弹簧的等效刚度,是弹簧机构弹簧刚度ks1折算到末端的等效刚度和驱动机构回转结构刚度的综合。
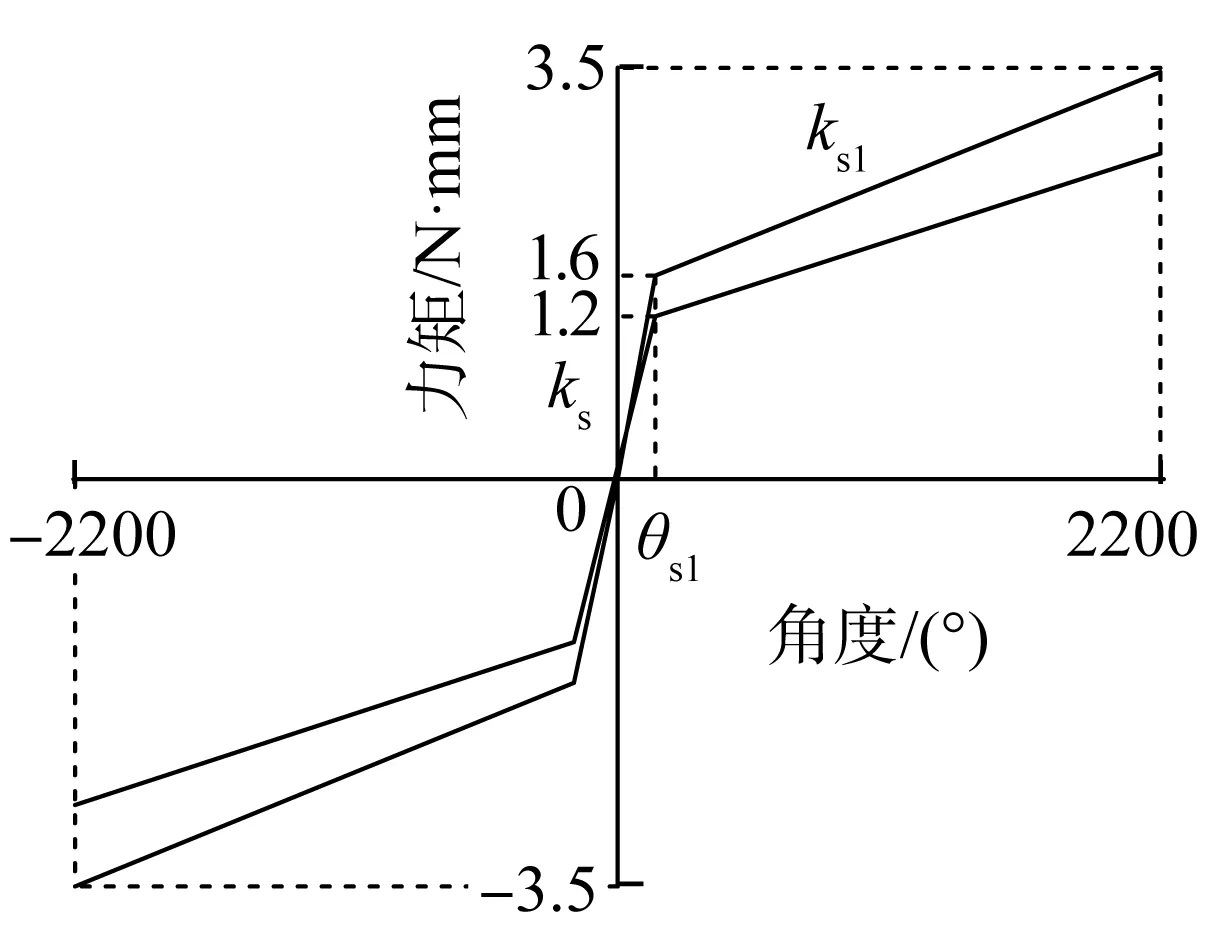
图3 弹簧机构特性曲线Fig.3 Characteristic curve of spring mechanism
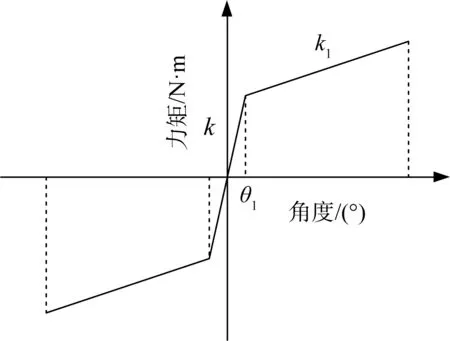
图4 驱动机构等效刚度特性曲线Fig.4 Equivalent stiffness characteristic curve of driving mechanism
弹簧机构的弹簧刚度等效到驱动机构末端的刚度k1e为:

当k≥k1e时,有k1=k1e。
当外负载力矩小于驱动机构末端等效弹簧初始力矩时,k与传动齿轮接触刚度、轴的扭转刚度相关。
2)等效阻尼系数。
定义阻尼器的等效阻尼系数为c,驱动机构的等效阻尼系数为B,根据传动比关系,有:

k和B与制动过程的频率、振幅密切相关,制动过程可以由阻尼自由振动模型描述。
若以制动的前一刻作为起始时刻(t=0 s),则在匀速平稳状态下,关节扭角θ=0°,关节转速θ˙=ω0,其中ω0为起始时刻驱动机构输出角速度。
t=0 s时驱动机构在制动过程的运动特性可以简化表示为:

已知要求ω0=0.14°/s,取k∈[100,1 500]Nm/°,根据式(6)和不同工况下驱动机构的等效阻尼系数(如表1所示)求解制动力矩和关节扭角,得到4组制动力矩—刚度和扭角—刚度特性曲线,如图5所示。

表1 不同工况下驱动机构的等效阻尼系数Table 1 Equivalent damping coefficient of driving mechanism under different working conditions
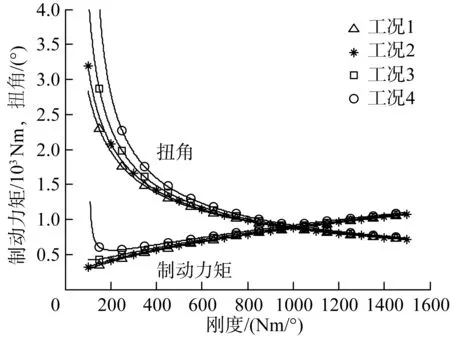
图5 制动力矩—刚度和扭角—刚度特性曲线Fig.5 Characteristic curves of brake torque-stiffness and torsion angle-stiffness
由图5可知:当k>210 Nm/°时,θ随着k的增大而减小,T随着k的增大而增大;当k>400 Nm/°时,B对θ影响的敏感度明显减小。
为了提高大惯量负载制动过程的稳定性,取θmax=1°,B=3 000 Nms/°,得到k=810 Nm/°。
1.2.3 传动比分配
已知c=2×10-5Nms/°,确定i2·i3≈8 682。由前文分析确定i1·i2≈235 000。
弹簧机构初始力矩Ts0与驱动机构末端等效弹簧初始力矩T0的关系须满足:

式中:η为弹簧机构到末端输出的传动效率,按照航天空间机构应用的经验数据,在601EF真空油脂润滑条件下,4级直齿传动时取η=0.85;T0可以根据驱动机构回转结构等效传动刚度和制动扭角得到。
根据式(7),计算得到i2≥430.3。最终根据实际齿轮传动参数设计得到传动比分配如下:
电机到弹簧机构为5级直齿传动和1级行星齿轮传动,i1=535.33;
弹簧机构到末端输出为3级直齿传动和1级行星齿轮传动,i2=439.75;
弹簧机构到阻尼器为3级直齿传动,i3=19.75。
2 驱动机构动力学分析和验证
2.1 驱动机构启动和制动仿真分析
显然,上述负载驱动机构的数学模型和参数计算忽略了传动链空程、齿轮啮合刚度和阻尼、传动效率、系统摩擦阻尼、弹簧机构滞回等非线性特性。为了进一步验证负载驱动机构的真实运动特性,须将上述非线性特性反映在仿真计算模型中,并将仿真结果与实验结果进行比对和互验。
1)传动链空程。
负载驱动机构传动链空程由齿轮传动侧隙引起。侧隙Jt=φ·dP/2,式中:dp为节圆直径,φ为转角。为适应空间高低温环境,采用中等齿轮侧隙进行设计[20]。
2)齿轮啮合刚度和阻尼。
全齿啮合法向刚度kbn和啮合阻尼系数bbn分别为:
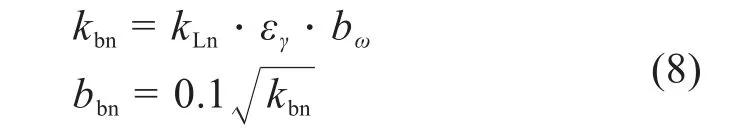
式中:kLn为直齿传动单对齿啮合刚度;bω为齿宽;εγ为齿牙接触比例。
为不失一般性,单对齿啮合刚度取通用值。
3)传动效率。
针对直齿传动、锥齿轮传动、行星传动的传动效率η1、η2、η3,须考虑轴承和联轴环节的黏性摩擦阻尼。
4)系统摩擦阻尼。
为了便于与实验结果进行比较,还应考虑系统摩擦力矩TF。其可通过实验系统实测获得。
5)弹簧机构滞回。
弹簧机构卷簧表面进行了MoS2黏结固体润滑涂覆,通过实测可以得到常温及高低温下的摩擦力矩损失比例Tf/T。由于弹簧机构卷簧在上紧和释放过程中的摩擦力矩方向相反,因此上紧和释放时相差2倍的摩擦力矩。
仿真采用多学科领域系统动力学建模和仿真软件Simulationx。仿真模型的非线性参数设置如表2所示。

表2 驱动机构动力学仿真模型的非线性参数Table 2 Nonlinearparameters ofdynamic simulation model of driving mechanism
按照传动刚度模型、有/无弹簧机构缓冲和有/无阻尼器耗能等,将驱动机构仿真工况分为6种,如表3所示。
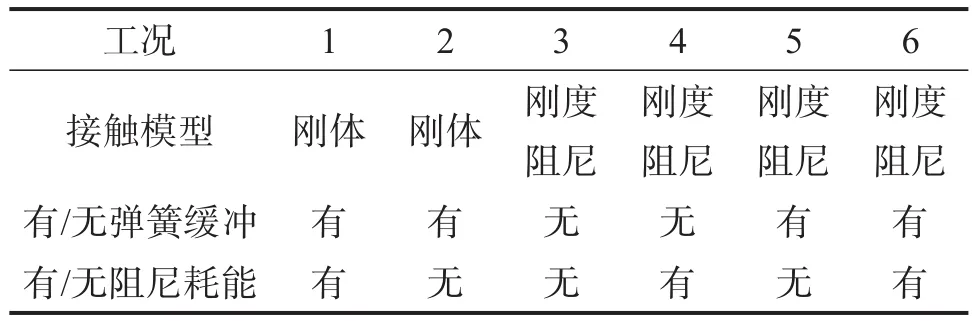
表3 驱动机构仿真工况Table 3 Simulation conditions of driving mechanism
仿真时长为1 000 s,转角行程为117°,大惯量启动和制动仿真结果如图6所示。
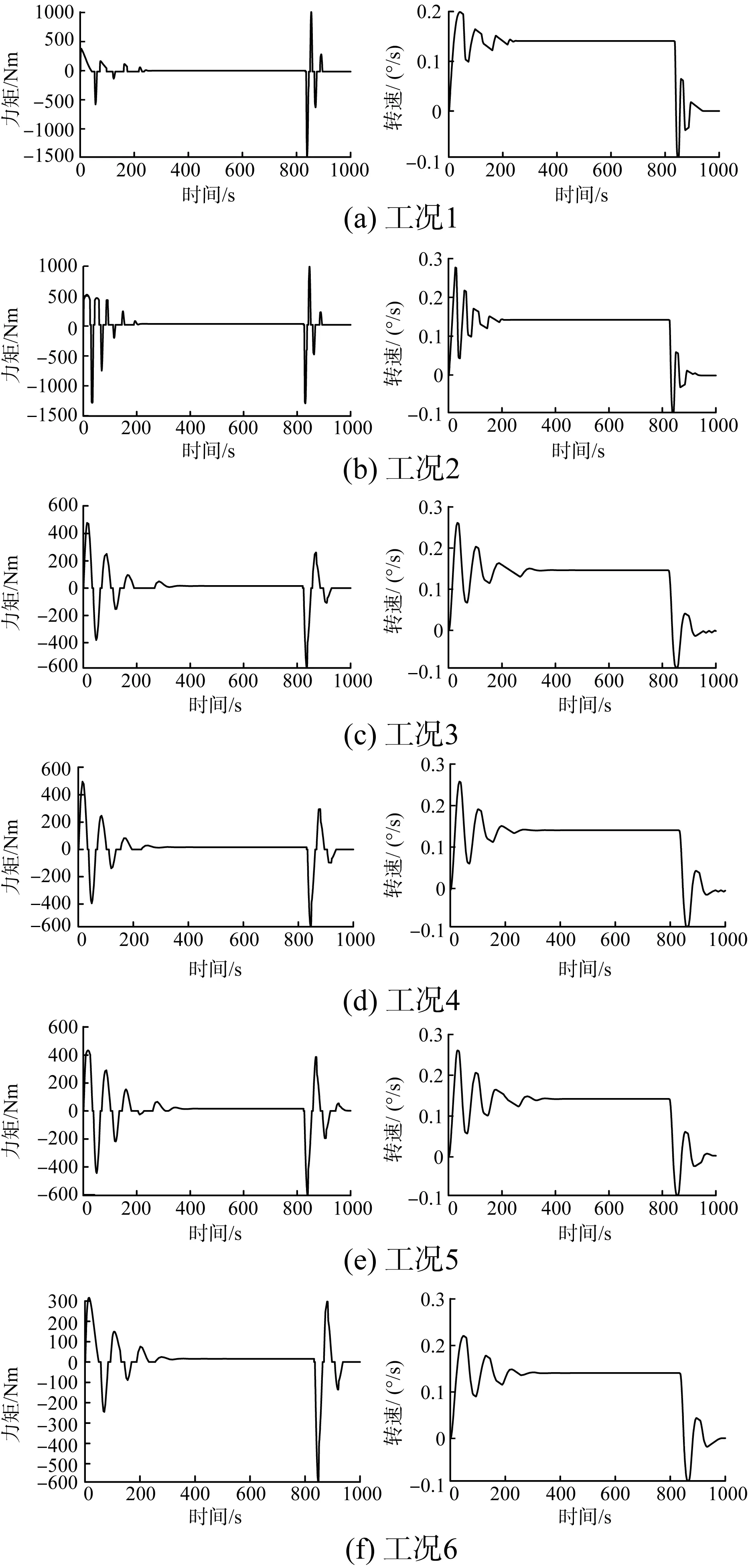
图6 大惯量启动和制动仿真结果Fig.6 Simulation results of large inertia starting and braking
仿真结果表明:
1)结构刚度对驱动机构启动和制动过程的平稳性具有显著影响;
2)考虑结构刚度后,驱动机构在启动和制动过程的力矩峰值均显著下降;
3)增加缓冲阻尼后,驱动机构在启动和制动过程的力矩峰值和速度稳定性均得到明显改善。
2.2 弹簧阻尼特性测试
为了得到真实的驱动机构等效弹簧阻尼特性,通过反向加载的方法对驱动机构120°、240°两个工作位置进行正反向弹簧阻尼特性测试,以获得驱动机构实际的刚度和阻尼特性。加载速度为0.08°/s,测试得到驱动机构的力矩—角度、力矩—时间曲线,分别如图7、图8所示。
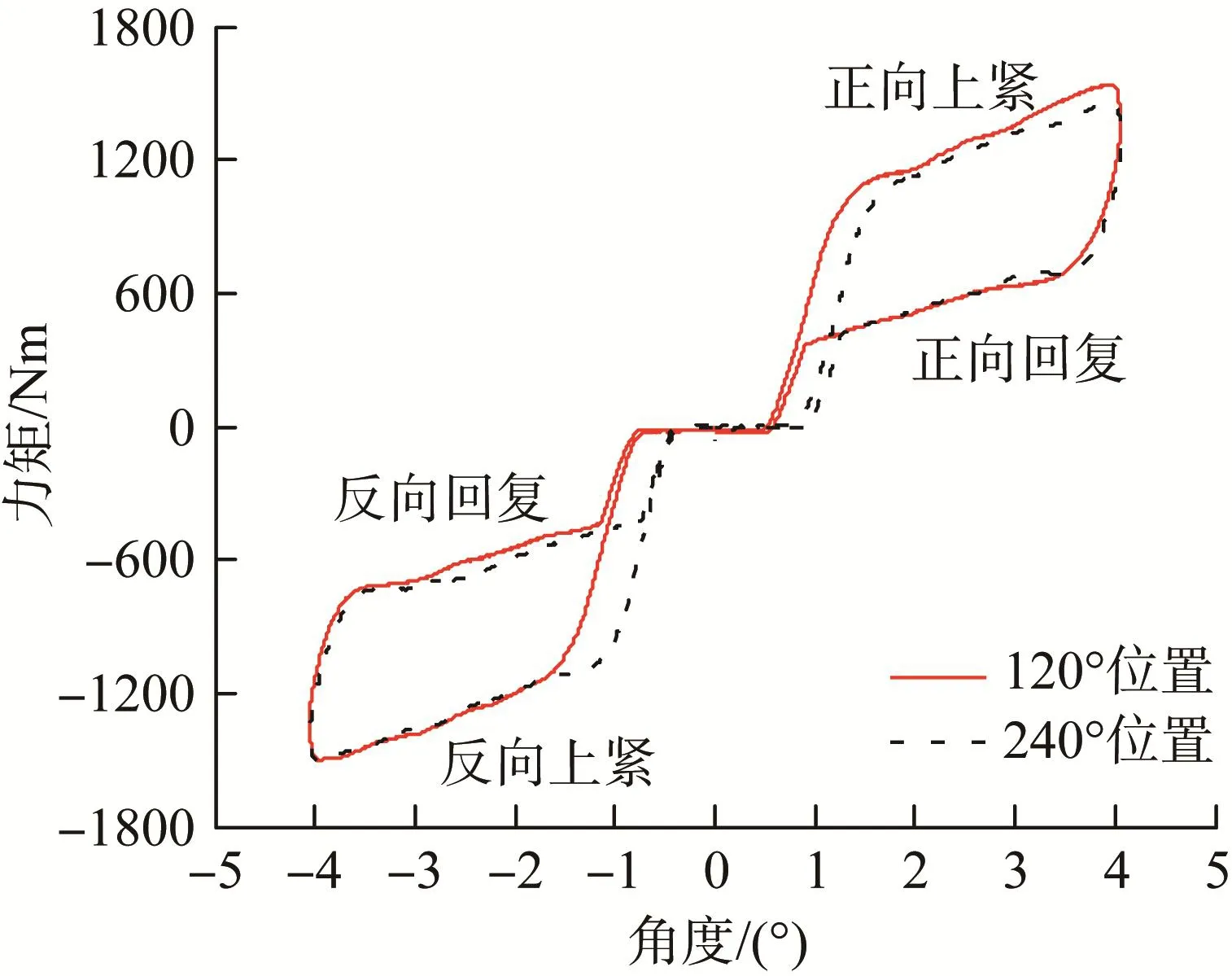
图7 驱动机构的力矩—角度测试曲线Fig.7 Torque-angle test curve of driving mechanism
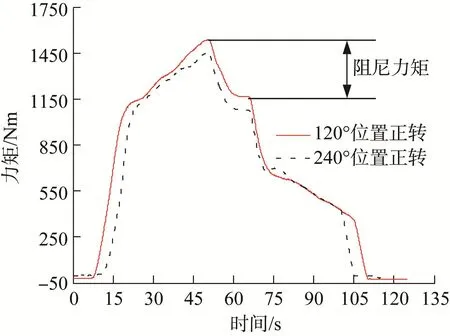
图8 驱动机构的力矩—时间测试曲线Fig.8 Torque-time test curve of driving mechanism
由测试曲线可知:
1)由于机构传动空程(约0.7°)的存在,2条曲线存在角度相位错移,但测试结果基本一致;
2)正转和反转时的特性曲线具有良好的对称性,说明机构正反向性能较一致;
3)上紧过程和回复过程具有较明显的滞回特性,说明机构阻尼及摩擦耗能起到明显作用。实际测得摩擦阻尼力矩平均为310 Nm。取末端到阻尼器7级齿轮传动(1级行星、1级锥齿轮和5级直齿传动)效率为0.8,算得阻尼系数为3 100 Nms/°,与1.2节中设计结果的误差为3.3%。
4)结构等效刚度远大于弹簧机构等效刚度,与图4所示的驱动机构等效刚度特性相吻合。实际测得的结构等效刚度约为873 Nm/°,与1.2节中设计结果的误差为7.8%。
通过以上分析可知,该驱动机构弹簧阻尼特性与理论设计相吻合,可用于大惯量启动和制动实验验证。
3 大惯量启动和制动实验验证
3.1 实验目的
验证驱动机构对大惯量负载的驱动能力及其运动平稳性和运动精度,以评价其在实际工程应用的可行性。
3.2 实验方案
实验在我国航天某型号专研的大惯量加载性能实验系统上进行。大惯量加载性能实验系统的组成如图9所示,实物如图10所示。
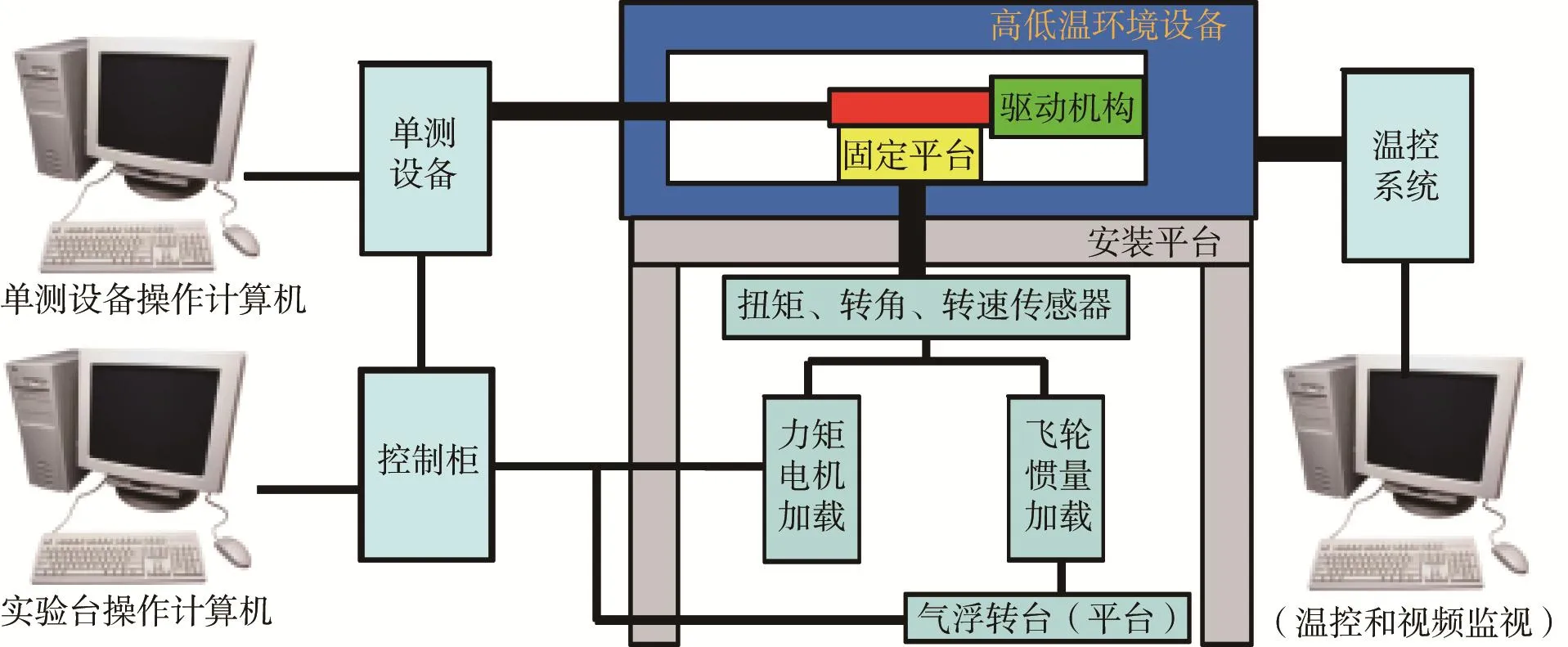
图9 大惯量加载性能实验系统的组成Fig.9 Composition of large inertia loading performance experimental system

图10 大惯量加载性能实验系统Fig.10 Large inertia loading performance experimental system
实验系统采用大飞轮质量盘实现大惯量加载,飞轮与驱动机构之间设置了1∶6增速器,以减小对飞轮质量的需求;固定平台用于驱动机构的安装和固定;气浮转台用于减小飞轮惯量加载系统自重引起的摩擦转矩;扭矩、转角、转速传感器分别用于测量关节的负载力矩、工作转角和转速;单测设备用于对驱动机构的驱动控制和信号采集;控制柜用于对实验系统的控制和信号采集,并与单测设备进行驱动机构实验状态信息的交互;高低温环境设备用于提供高低温环境,并且具有照明和视频监控功能;安装平台用于支撑负载模拟器和高低温环境设备。
3.3 实验结果及分析
实验中转动惯量为2.2×106kgm2,转动角度为117°,从0°转到117°,实验结果如图11所示。
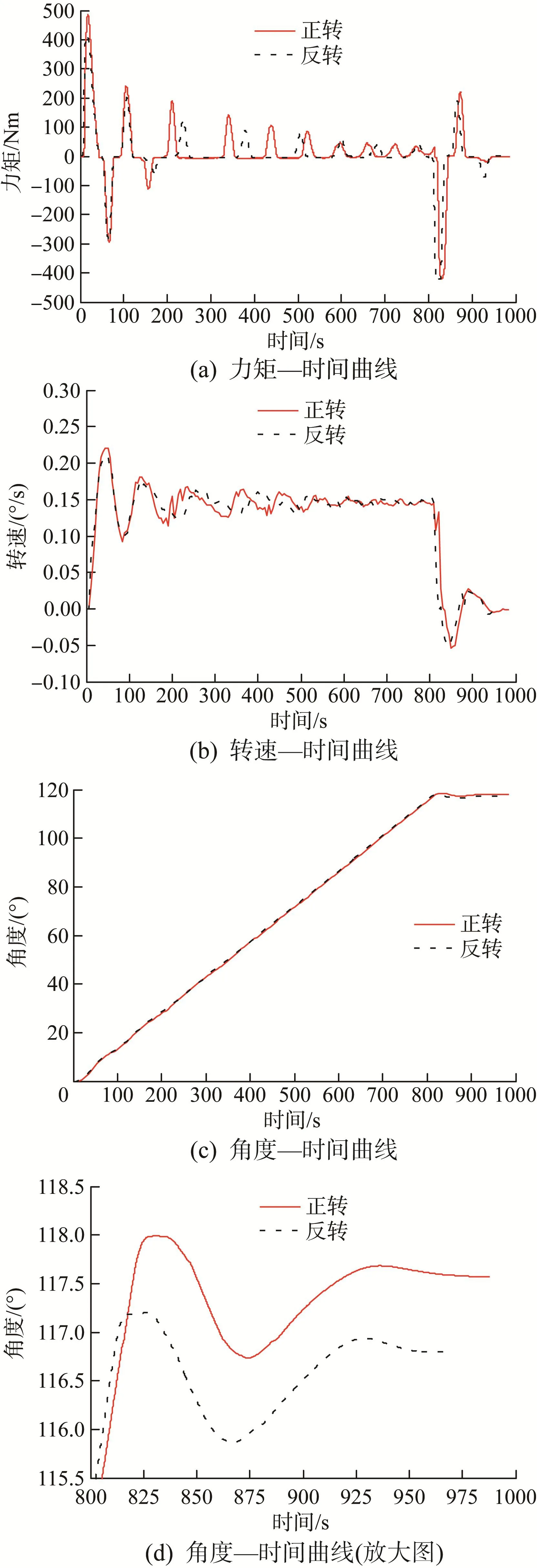
图11 大惯量启动和制动实验结果Fig.11 Test results of large inertia starting and braking
分析实验结果可知:
1)在机构正转和反转过程中,启动和制动力矩曲线、速度曲线均具有较高的重合度,且其峰值基本一致。
2)启动和制动力矩峰值为400~500 Nm,远小于驱动机构4 000 Nm的承载能力。
3)启动速度峰值为0.221°/s,稳定速度为0.14°/s,超调量约为50%,与图6(f)所示的仿真结果吻合。驱动机构输出的绝对速度较低,运行平稳。
4)制动过程持续1.5个振荡周期,运行3 min后驱动机构趋于停转,与图6(f)所示的仿真结果一致。角度的精度优于1°,包括了驱动机构自身空程角度,可见机构的运动精度满足工程应用要求。
5)根据表2所示的动力学参数算得最大启动力矩为320 Nm,最大制动力矩为580 Nm。最大启动力矩理论值比实验值小,最大制动力矩理论值比实验值大。显然,实验中联轴工装、飞轮惯量支撑轴承和增速器等同样起到了一定的缓冲效果。
6)根据式(6)算得的在制动过程中最大扭角为0.85°,考虑在制动过程中机构传动效率仍按0.8计算,得到制动过程的最大扭角为0.68°,与图11(f)所示的实验值(0.65°)的误差为4.4%,说明计算结果基本与实验结果吻合。
综上,通过在工况6下的实验结果与仿真结果的对比可知,振荡周期、启动时间、启动速度超调量和制动时间等曲线形态特征较一致。此外,由于实验中联轴工装和大质量飞轮惯量连接轴刚度和阻尼的影响,启动和制动力矩峰值、制动速度超调量的实验值较仿真值小,并使得在转速平稳工作段存在力矩和速度的小幅波动。
4 结论
设计了以小功率驱动大惯量负载的驱动系统,其已成功应用于我国空间站转位机械臂中。建立了具有多级齿轮传动、弹簧缓冲、阻尼耗能及电磁制动等功能的驱动机构,其能较好地实现大负载惯量的平稳启动、制动和停止时的精准定位。
实验结果表明,提高传动比可以降低电机端等效负载惯量,减小输出端负载变化引起的力矩波动。而大减速比传动带来的驱动输出效率的降低对低速大负载转动惯量驱动的影响并不显著。
虽然实验中驱动机构和试验工装结构刚度的影响无法解耦,但通过对在一定范围内等效刚度和等效阻尼的影响分析,表明该驱动系统可以满足工程应用的要求。
