硅质轻型墙板材料受压性能试验研究

2022-03-10王松岩李建民焦红刘学光马海程

新型建筑材料 2022年2期

王松岩，李建民，焦红，刘学光，马海程

（1.山东建筑大学土木工程学院，山东济南 250101；2.济南中建建筑设计院有限公司，山东济南 250101）

0 引言

为适应装配式建筑发展，解决建筑行业面临劳动力短缺，人工成本急剧上升等一系列问题[1-2]，2016年国务院颁布《关于大力发展装配式建筑的指导意见》，文中明确指出，大力发展装配式建筑是推动我国建筑产业现代化重要的途径之一。装配式墙板的推广与应用将推进绿色建筑发展，对实现经济和社会可持续发展有着重大意义[3]。

GLC硅质轻型墙板（以下简称GLC墙板）是以硅质材料为主要原材料，掺加增强剂、防水剂、发泡剂、稳泡剂等外加剂，经湿法成型工艺，并在正反面层以耐碱玻纤网增强，复合成型的轻质板材。墙板的构造如图1所示（以100mm厚度为例）。

我国装配式建筑起步较晚，对于新型墙板材料的力学性能研究还存在着很多不足，目前市面上常见的墙板材料主要有蒸压加气混凝土、发泡水泥、水泥基、EPS泡沫混凝土、陶粒混凝土等。曾欢[4]对蒸压加气混凝土试件进行了单轴抗压试验，得到立方体抗压强度和轴心抗压强度之间的关系，分析了试件的主要破坏形式。陈瑞芸[5]对发泡水泥墙板材料进行力学性能研究，计算出单轴受压本构模型，并通过有限元研究发泡水泥芯材及钢筋骨架组成墙板的力学性能，为墙板研究提供理论依据。张聪等[6]研究了钢纤维（SF）-聚乙烯醇（PVA）纤维增强水泥基的压缩应力-应变全曲线，基于损伤力学理论，从能量角度提出了一种新的单轴压缩本构模型。熊耀清和姚谦峰[7]对蒸压加气混凝土和泡沫混凝土进行轴心受压试验，并通过上升、下降和斜直线3种公式拟合了轻质多孔混凝土的应力-应变曲线。

GLC墙板作为一种新型复合墙板，国内外学者缺少对其材料本构关系的研究。因此，本文通过对GLC墙板材料进行单轴受压试验，得到其基本力学性能，提供了墙板材料的本构关系模型，并求出墙板力学性能计算公式，为GLC墙板有限元分析与结构设计提供理论参考。

1 砂浆及芯材单轴受压试验

1.1 试件设计与制备

本试验芯材试件以硅质材料为主要原材料，掺加发泡剂、增强剂等外加剂，经化学发泡成型后，放置在不低于20℃干燥环境下，养护15 d制成。其中增强剂配合比为50%硅灰、30%纳米晶须、0.4%9~15 mmPP纤维、1.6%30~50 mm棕丝；发泡水泥芯材水胶比为0.5，配合比为2.5%增强剂、70%水泥、25%粉煤灰、3%发泡剂。

砂浆和芯材的试验设计及试验方法参照JGJ/T 70—2009《建筑砂浆基本性能试验方法》和GB/T11969—2008《蒸压加气混凝土性能试验方法》。制备4组24块砂浆试件与发泡水泥芯材试件，编号分别为SC1～SC6、SCP1～SCP6、FC1～FC6、FCP1～FCP6。其中SC与FC编号分别为砂浆和发泡水泥芯材立方体抗压强度试件，尺寸分别为70.7 mm×70.7 mm×70.7 mm、100 mm×100 mm×100 mm；SCP1～SCP3与FCP1～FCP3编号分别为砂浆和发泡水泥芯材轴心受压试件，SCP4～SCP6与FCP4～FCP6编号分别为砂浆和发泡水泥芯材弹性模量试件，SCP与FCP编号试件尺寸分别为70.7 mm×70.7 mm×212 mm、100 mm×100 mm×200 mm。

1.2 加载方案及测点布置

本试验在山东建筑大学力学实验室进行，采用600 kN微机控制电液伺万能试验机。试验加载速率为0.5 kN/s。当立方体抗压试件出现破坏或明显变形时停止加载。弹性模量试验时，先取SCP1～SCP3、FCP1～FCP3进行轴心抗压试验，后对剩余试件反复预压3次，按照0.5 kN/s速率缓慢加载，试验加载曲线如图2所示，当试件前后两侧变形值得读数小于0.2%时，加载至破坏。为方便测量试件的弹性模量与泊松比，在试件四面中线位置分别贴50 mm应变片，测量装置均连接TZT3826E数据采集系统进行数据采集。弹性模量按式（1）进行计算。

式中：F0.4——应力为0.4fc时对应的棱柱体试件压力，N；

F0——应力为0.3 MPa时对应的压力，N；

A——棱柱体受压试件面积，m2；

Δl——试件最后一次由F0加载至F0.4时试件两侧变形差的平均值，m；

l——测量标距，m。

1.3 试验现象

采用数理统计的方法，对每组试验数据及现象进行分析筛选，取其中具有代表性的试件进行描述，试验现象如下：

砂浆试件的破坏形态基本相似：加载初期，试件均无裂缝产生；荷载加载至峰值应力的60%时，试件端部出现纵向裂缝，随荷载的不断增加，裂缝向下延伸，并伴随劈裂的声响；加载至峰值应力时，纵向裂缝上下贯通，试件表面大面积起皮、剥落现象严重；随后荷载急剧下降，试件被破坏成多个小柱，发生劈裂破坏，砂浆试件的典型破坏形态如图3所示。

芯材试件因采用发泡工艺，表现有较好的延性，加载初期并无裂缝产生；当加载至峰值应力的80%时，芯材试件端部出现多条不连续的、细而长的纵向裂缝；随荷载的不断增加，裂缝向下延伸，相近的纵向裂缝相连形成斜裂缝；加载至峰值应力时，裂缝不断变宽，形成贯通芯材试件的全截面主斜裂缝；随后承载力下降，试件破坏。芯材试件的典型破坏形态如图4所示。

2 试验结果及分析

2.1 应力-应变全曲线

取SCP与FCP组试验数据整理分析，得到试件单轴受压应力下的应力-应变全曲线，如图5所示。

由图5可知：（1）砂浆作为脆性材料，在受压过程中试件表面易产生裂缝，对应变片数据采集影响较大，因此造成采集的应力-应变曲线离散性较大；芯材抗压过程中裂缝出现较少，故曲线离散性较小。（2）在曲线上升段，随着应变的增加，砂浆应力-应变全曲线先达到峰值应力点，说明砂浆极限压应变小于芯材应变，但因弹性模量相差较大，砂浆峰值应力大于芯材峰值应力。（3）曲线下降段中，芯材试件因本身存在大量孔洞，当到达试件的最大承载力时，孔洞被压缩，试件被压密实，承载力趋于稳定，残余应力较高。

2.2 峰值应力与峰值应变

对试验数据分析处理得到2种试件的峰值应力与峰值应变，结果为砂浆立方体试件的平均峰值应力即立方体抗压强度为7.12 MPa，棱柱体试件的平均峰值应力即轴心抗压强度为6.53 MPa，对应的平均峰值应变为1.69×10-3；同理，芯材的立方体抗压强度、轴心抗压强度与对应的平均峰值应变分别为3.81 MPa、3.15 MPa、2.26×10-3。得到2种轴心抗压强度与标准立方体抗压强度之间的关系式：

式中：fc1、fc2——砂浆、芯材轴心抗压强度，MPa；

fcu1、fcu2——砂浆、芯材立方体抗压强度，MPa。

芯材在制作过程中加入发泡剂，在材料中产生了大量均匀稳定的气泡，形成了一种有大量气孔的均质材料，在加载过程中，试件的承压面积的约束范围作用较小，导致立方体的破坏形态和极限荷载与棱柱体的基本相近，强度提高有限[8]。此外，有研究表明[9]，在进行单轴受压试验时，试验机与试件端部摩擦因数大于0.04时，立方体抗压强度接近棱柱体强度，砂浆试件因在试验过程中没有充分考虑立方体试件与千斤顶之间摩擦力的影响，导致试件在受压过程中未处于单轴受压应力状态，立方体试件极限荷载比棱柱体极限荷载提高不大。

2.3 弹性模量与泊松比

2种试件实测弹性模量与泊松比见表1，其中，E1代表公式实际计算的弹性模量、E2代表试件在应力上升段σ=0.4σm对应的弹性模量、ν表示泊松比，计算公式为ν=ε'/ε，具体取值按应力上升段σ=0.4σm时对应的应变值取值。砂浆试件的弹性模量、泊松比的取值分别为6500 MPa、0.200；芯材试件的取值分别为1650 MPa、0.272。

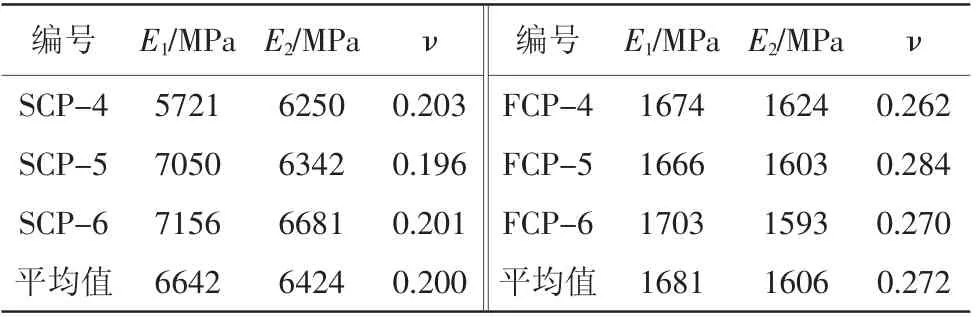
表1 弹性模量与泊松比

3 GLC墙板材料单轴受压本构关系

文中2种材料所计算的应力-应变全曲线公式，以混凝土本构关系为模型推导出来。将各组实测应力-应变全曲线无量化，得到试验数据绘制出2种材料基本的应力-应变全曲线模型如图6所示。

式中：σm——峰值应力，MPa；

εm——峰值应力所对应的应变。

3.1 应力-应变全曲线数据拟合

国内外学者对应力-应变关系曲线采用指数型、多项式、有理分式模型进行描述[10-12]。根据图6所示应力-应变全曲与试验数据试探性拟合，分别采用五次多项式和有理分式非线性拟合上升段和下降段的试验数据，拟合方程如下：

上升段：

下降段：

把图6描述的几何条件代入式（5）、式（6），可以求出A0=0、A4=5-4A1、A4=3A1-4、B1=1-2B0、B2=B0，试件受压应力-应变全曲线公式可简化为：

上升段：

下降段：

式中：E0——试件初始切线模量，N/mm2；

EP——试件峰值割线模量，N/mm2。

在式（10）中可以看出，A值为试件初始割线模量与峰值割线模量的比值。由经验可知，EP＞0，且A=＞1；对式（9）再一次求导得到，当x=1时，≤0，可以求出A≤≈1.67；可求得A值得取值范围：1≤A≤1.67。

对于下降段控制参数B，把0≤y≤1代入式（8）可得0≤B＜∞。利用ORIGIN软件对全曲线进行拟合，拟合曲线与试验曲线对比分析如图7、图8所示。

3.2 本构关系数值确定

根据理论分析与试验数据的相互拟合，最终确定了砂浆与芯材的全应力-应变全曲线方程。砂浆的取值为：A=1.46，B=1.20；芯材的取值为：A=1.03，B=11.2；残余强度系数为0.641。具体计算方程如式（11）、式（12）所示。

砂浆：

芯材：

试验曲线与拟合曲线如图9所示，拟合参数如表2所示。

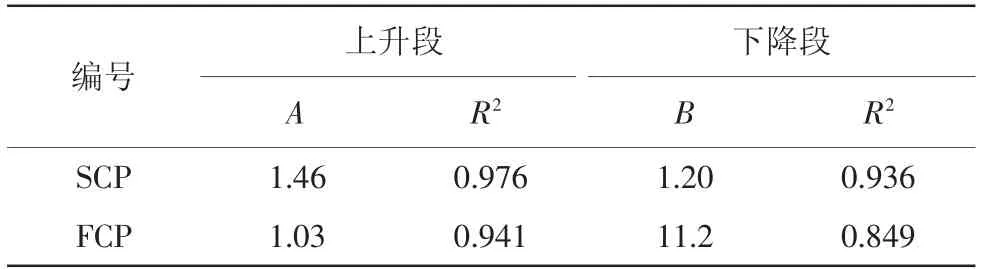
表2 试件应力-应变全曲线拟合参数

由表2可知，上升段拟合效果较好，R2在0.941以上，下降段R2在0.849以上。因试验在加载过程中使用的荷载加载方式，当达到峰值荷载时，荷载突然下降，导致应变片下降部分收集的数据比较少，只能结合万能试验机数据分析；而ORIGIN软件进行非线性曲线拟合时，受数据分布点密集程度的影响比较大，下降段拟合效果不好。

4 GLC墙板力学性能分析

GLC墙板作为复合材料，墙板受力由发泡水泥芯材与表皮砂浆共同承担。对于2种不同性质合成的复合材料，取隔离体受力分析，忽略耐碱纤维玻璃网的作用。假设材料在外力作用下不同材料接触面上的几何变形均匀一致，砂浆和芯材共同受力变形，求得抗压强度与弹性模量，如图10所示。

将式（13）和式（14）相加得：

墙板材料整体又满足：

式

（14）代入式（15）得：

同理可求：

式中：FC——GLC墙板抗压强度，MPa；

E——GLC墙板弹性模量，MPa；

V1——面层砂浆所占体积比；

σ1、σ2——砂浆、芯材轴心抗压强度，MPa；

E1、E2——砂浆、芯材弹性模量，MPa。

因GLC墙板试件与单块砂浆、芯材的受力机理不同。芯材、砂浆试件在受压过程中两面受压、四面受拉；而墙板试件在受压过程中因2种材料力学性能不同，砂浆与芯材相互阻碍变形，受力机理更加复杂，因此在式（17）、式（18）中引入修正系数k来表示。结合文献[13]对墙板试件基本力学性能试验，初步确定修正系数k=1.15。GLC墙板平均抗压强度和弹性模量求取公式改为：

根据试验所得砂浆与芯材的轴心抗压强度与弹性模量带入式（19）、式（20），求得FC与E分别为4.18、2832 MPa，并与文献[13]比较（4.21、2734 MPa），计算结果与文献试验结果吻合较好。