数学“转化思想”的教学

摘 要：在当前的课程改革中，基于培养学生的核心素养，对学生的学习能力要求越来越高. 授之以鱼，不如授之以渔.让学生认识、理解数学思想方法是新课程的任务，让学生学会使用这些思想方法是我们教学的一项重要目标.本文从以下三个方面论述了转化思想的教学：（1）正确理解转化思想的内涵是有效使用转化思想的基础;（2）明晰转化思想的使用原则是有效使用转化思想进行解题的有效保证;（3）明晰转化思想的形式内容是准确运用转化思想的重要条件.

关键词：转化思想;新课程改革;数学思想方法

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2022）02-0002-03

作者简介：张丽敏（1983.9-），女，福建省建宁县人，本科，中学一级教师，从事中学数学教学研究.

在当前的课程改革中，基于培养学生的核心素养，对学生的学习能力要求越来越高. 授之以鱼，不如授之以渔.让学生认识、理解数学思想方法是新课程的任务，让学生学会使用这些思想方法是我们教学的一项重要目标.

数学转化思想是初中阶段学生需要学习的最重要、最基本、同时也是应用最普遍的数学思想之一.那么，在初中阶段，应当怎样实施“转化思想”的教学任务呢？

1 准确理解转化思想的内涵是有效运用转化思想的根本

转化思想源于普通的数学知识，但是又凌驾于普通的数学知识之上，所以，在教学时应该注意渗透知识蕴含的思想方法，并且在掌握了必要知识的前提下，对相应的思想方法做出恰当的归纳.包括：（1）由繁杂到简单;（2）由困难到容易;（3）由未知到已知.即把一个陌生的、不熟悉的、相对繁杂的、需要处理的新问题，经过恰当的转换，化归为一个熟谙的、简单的或已经处理了的旧问题，这就是转化思想. 所以，我们也称转化思想为化归思想.

2 明晰转化思想的使用原则是有效使用转化思想进行解题的保证

2.1 将隐蔽性的条件转化成数学语言并清楚地表述出来

例如：在分析应用题中的销售问题时，往往要用到这样的等量关系：利润=收入-成本、收入=销售量×售价、单件利润=售价-进价等等，而这些等量关系一般不会在题中直接体现，这时候就需要自己明晰这些隐藏的关系.在几何题中也时常会碰到必须转化隐藏条件的情况，如：已知等腰△ABC两条边分别为4cm和9厘米，求△ABC的周长.本来按分类讨论的思想第三边为4cm或9cm，但图形为三角形，应考虑隐藏条件：任意两边之和大于第三边，若第三边长为4cm，则不满足三边关系，所以第三边只能为9cm，周长22cm.又如对顶角、公共角、公共边，均属于隐藏条件，通过观察图像，推出角相等或边相等，用符号表述.

2.2 尽可能地直观、形象

把信息尽可能转化成图形、示意图，并用醒目的符号进行标记，使已知、未知及其之间的关系一目了然，从而使思维更加简捷、直观.

比如求证：等腰三角形两条腰上的高相等. 结合已知条件“一个三角形是等腰三角形，两条腰上各有一条高”，画出一个等腰△ ABC及腰AB、AC上的高CD、BE，并结合图形写出已知： 在等腰 △ABC中，CD⊥AB交AB于点D、BE⊥AC交AC于点E.求证： CD=BE.又如线段或角的和差倍数求解，按要求画出图形，结合条件在相应图形上做出长度或角度的标记，就便于观察、进行直观判断.尤其涉及几何综合题，面对复杂多变的条件，将条件在图形中进行标记就更有必要了.

2.3 善于联想

根据题目所给的条件，首先想起（1）与题目有关联的概念、定理、性质、规律等基础知识和基本解法;（2）猜到或许要用的解题策略;（3）想到已经解过的题型;（4）想到与题目相似的、甚至是相反的信息，达到将新问题转化为已经解决过的旧问题的目的.其次进行类比的手法，采用特殊化或者一般化等途径分析新问题，从而得到处理新问题的要领，以解决新问题.

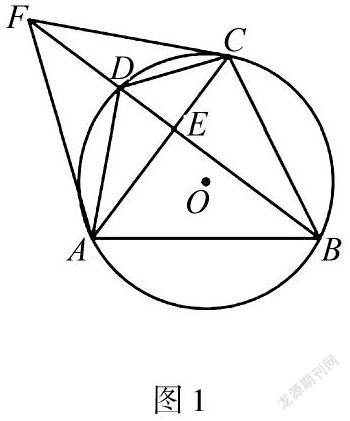
例如2019年福建省中考数学试题第24题：如图1，四边形ABCD内接于⊙O，AB=AC，点F在BD的延长线上，DF=DC，AC⊥BD，垂足为E，连接AF、CF，AF=10，BC=4.

（1）求证：∠BAC=2∠CAD;

（2）求tan∠BAD的值;

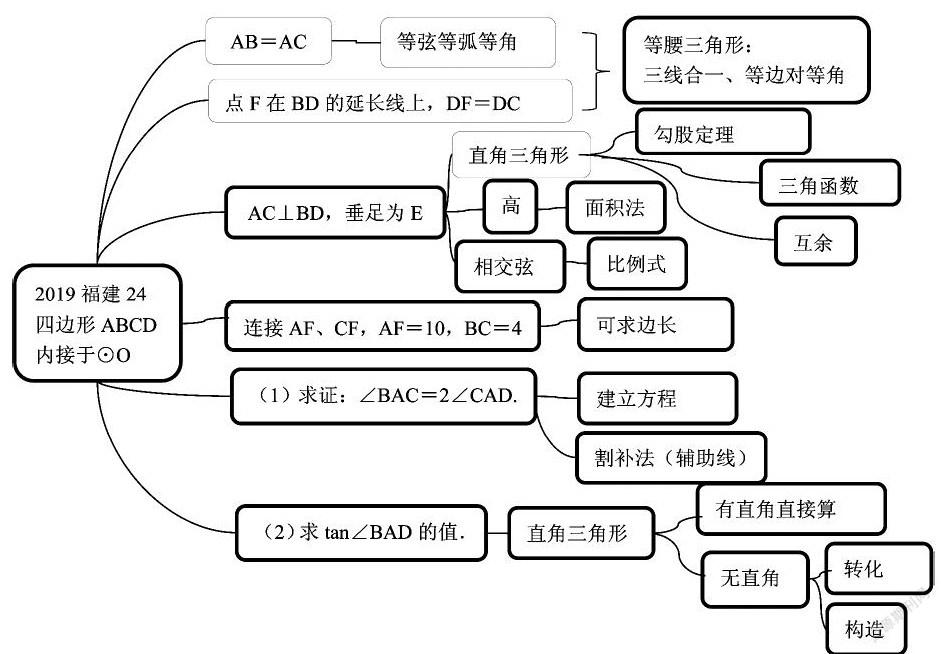
综合2.1;2.2，使用思维导图对本题涉及的基本知识、解法、解题方向、题型等展开联想：

学生对题目理解困难的重要原因之一就在于不会整理信息并展开联想，第（1）小题，以建立方程为解题方向，结合思维导图，观察角的隐藏条件，如同弧所对圆周角相等，三角形内角和180度并在图形中标记，综合联想到的有关角互余和等弦等角或等腰三角形两底角相等的结论，确定角之間的和差倍数关系，列出方程，进行化简即得两角的二倍关系;第（2）小题，根据条件及图形判断∠BAD没有在直角三角形中出现，已知的直角三角形中也没有和它相等的角，所以必须构造∠BAD所在的直角三角形，于是引出辅助线：过D点作DG⊥AB于点G，构造直角三角形AGD，运用相交弦得比例式或面积法列方程求解相关线段长度，最后根据正切函数的定义求值.

所以，联想是突破思维瓶颈的有效方式，根据联想的内容进行整合，综合把握可以有效突破难题.

2.4 争取化繁为简

如果题目给的条件或结论中出现结构比较复杂的内容，就要先用简便形式体现，再用简洁的语言展示出来，使条件或结论简化.

如销售问题，由于涉及大量数据，如果不能简化信息，阅读时会存在一定的困难甚至出错，用表格形式整理信息就很有必要.列举出不同物品的进价、标价、售价、销售量、利润，使数据按类别排列，达到化繁为简的目的，量与量之间的关系在表中也一目了然，再结合

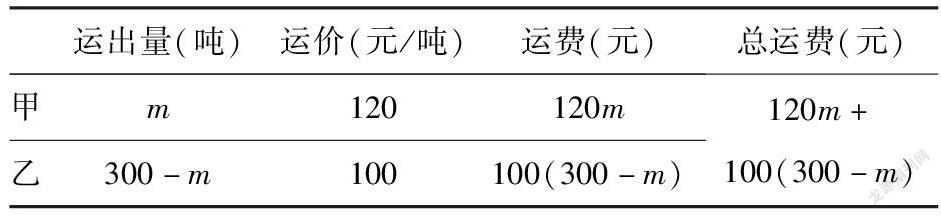
2.1中提到的运用隐藏的等量关系，易得方程.又如运输问题：某公司在甲、乙两仓库分别存放一种原料240吨和210吨.（1）如果运出甲仓库所存原料的60%，乙仓库所存原料的40%，求从甲乙两仓库共运出原料多少吨;（2）公司需要将甲、乙两仓库共300吨原料运往工厂，其中甲仓库运出m吨，从甲、乙两仓库到工厂的运价分别为120元/吨和100元/吨.求总运费（用含m的代数式表示）.（1）相对简单，（2）条件不进行简化整理则不易理清条件关系，以（2）为例简化如下表：

2.5 重视解后研究

归纳解答一道题目的经验，思考该题是不是可以拓广，解法是否可以推广？能运用在其他题目上吗？若能，拓广出的新内容则又转化成了新的结论，也加强了学生对转化思想的了解、促进了使用转化思想的能力提升，进一步达到解一题通一类的目的.例如在2.3善于联想中提到2019福建省中考数学试题第24题，通过进一步思考，可以归纳出：圆或多边形的问题通常通过添加辅助线，转化为特殊四边形或三角形，而求解线段或角度的问题就是构建方程，达到解决这一类问题的目的.也正是因为之前对相应类型题的解后研究，提供该题的思路.

3 明晰转化思想的形式内容是准确运用转化思想的重要条件

3.1 局部转化

即将题目中的条件或结论进行逐步转化，一般分为顺推转化和逆推转化.

顺推转化即转化已知条件，推出结论.例如求证：对角线互相垂直的平行四边形是菱形.证明思路即是通过将“对角线互相垂直”的条件推导转化为“一组邻边相等”，从而利用菱形的定义证出该命题成立.

逆推转化即转化结论为新问题，通过解新问题得出最终结论.例如已知x+y=7，xy=2，1x+1y的值是多少？从问题出发，将原式进行通分，化为分母是xy，分子是x+y的分式，再将对应值整体代入即得.如果题目比较复杂，也可以两种方式结合使用.

3.2 整体转化

将旧问题细化为若干个新的问题，只要将这些新问题解决了，原来的旧问题也就解决了.例如：在平面直角坐标系中，已知△ABC的三个顶点坐标A（3，6）、B（1，2）、C（6，5），求△ABC的面积.

条件是各个顶点的坐标，要求是三角形的面积.如果直接求解，容易使用勾股定理求出各条边的具体长度，但是难以求出边上的高，所以不易直接求出面积，这时候怎么办呢？转换思路：在△ABC的外部构造矩形DBEF，将条件中三个顶点坐标转化成矩形的长、宽及Rt△ADB、Rt△BEC、Rt△AFC中直角邊的长度，将要求的问题△ABC的面积转化成求矩形DBEF、Rt△ADB、Rt△BEC、Rt△AFC的面积，再用矩形DBEF的面积减去三个直角三角形的面积和即得△ABC的面积.

转化的过程可以表现在不同的层次上，也可以表现在不同内容之间，比如代数与几何之间，有的就出现在解决某个具体问题的过程中.

总之，转化思想方法（也称化归思想方法）几乎时时刻刻存在于每个问题当中.数学转化思想的教学也不是一时半刻就能完成的，需要教师们结合教材的具体内容反复进行教学指导，需要学生不断努力学习才能真正掌握.

参考文献：

[1] 陈欣龙.转化与化归思想在数学解题中的应用[J].成才之路，2009（23）：50-51.

[2] 许青林.中学数学化归思想及其应用[J].吕梁高等专科学校学报，2007（01）：61-63.

[3] 冉茂清.基于新课程的初中数学思想方法的教学研究[D].重庆：重庆师范大学，2011.

[4] 吴谦.中学数学中常用的思想方法[J].内蒙古电大学刊，2008（01）：94-95.[5] 周佩青.转化思想在数学解题中的妙用[J].教育教学论坛，2013（18）：86-87.

[责任编辑：李 璟]

3881500338209