阻塞干扰双频钝感效应规律与作用机理

赵 凯 魏光辉

(陆军工程大学石家庄校区电磁环境效应国家重点实验室 石家庄 050003)

1 引言

随着信息技术的飞速发展和电子设备的广泛应用，各种电磁信号在空域、时域、频域密集重叠，电磁环境更加恶劣，装备工作的可靠性以及生存能力受到严重威胁。当干扰信号进入接收机时，会使有用信号增益降低，导致装备性能降级甚至受损。准确预测装备在复杂电磁环境中的生存能力是提高其电磁防护性能的基础工作。

现行的抗扰度测试标准几乎都以单源、单频为背景，这与实际电磁环境有所出入[1-3]。有研究指出，通过单辐射源抗扰度试验后，装备可能会在强度较低的多辐射源环境中受到干扰，包括不同射频干扰和互调干扰的贡献[4-6]。在非互调干扰效应方面，根据阻塞干扰的机理，可将用频装备分为场强有效值敏感型和场强幅值敏感型两类，其中场强幅值敏感型对双频干扰更为敏感，针对这两种类型分别建立了干扰预测模型并进行试验验证[7-11]。然而，通过试验中发现，场强有效值敏感型装备在某些情形下对双频干扰表现出钝感，导致预测模型误差增大。

本文首先通过电路非线性失真分析，从理论上探索了场强有效值敏感型装备双频钝感效应规律与作用机理，而后以某型Ku波段频率步进雷达为受试装备进行试验验证，对提高用频装备电磁防护能力提供了技术支撑。

2 理论分析

接下来探究双频干扰中单个分量强度变化对干扰效果的影响。假定系统受到双频干扰，其中干扰分量1强度保持恒定，则干扰分量2对有用信号增益的影响可通过下式分析

上述对双频钝感效应的规律进行了理论分析，结合幂级数展开式中非线性系数的特性可知，a1,a5>0对有用信号起到了放大作用，而a3<0起到了阻塞作用。由此可认为，当系统开始出现非线性失真时，仅需保留幂级数展开式的a1与a3项，系统对干扰信号的场强有效值敏感，此时不存在钝感现象；随着非线性失真程度增加，a5项的作用不可忽视，致使双频钝感现象出现。下面通过开展雷达双频电磁辐射效应试验，对以上理论分析内容进行验证与完善。

3 试验验证

3.1 试验准备

受试装备为某型0中频体制Ku波段频率步进连续波雷达，工作频率为f0±100 MHz(f0为中心频率)，具备静目标测距功能，并可显示不同目标回波的电平[13]。具体试验布置如图1所示。使用两台信号发生器产生正弦连续波干扰信号，辐射天线同时充当雷达的探测目标。频谱仪通过定向耦合器监测干扰功率，并结合位置替换法与线性外推/内插法获取试验点处实际干扰场强[14]。

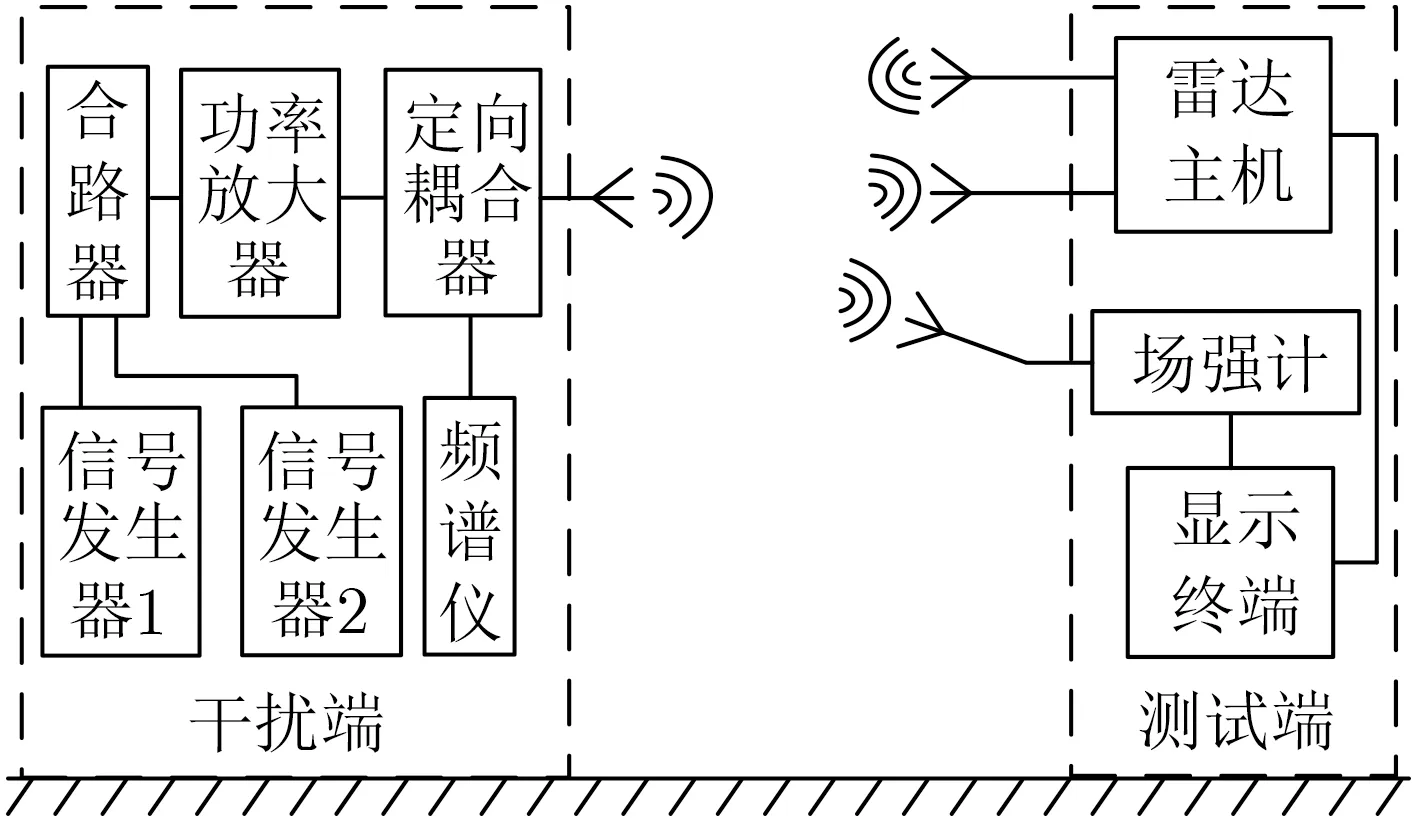
图1 试验配置图

试验中用目标回波峰值电平的压缩量反映有用信号增益的变化。一般来说，当增益压缩1 dB时，可认为系统出现了不可忽视的非线性失真[15]。为比较阻塞程度强弱对双频电磁辐射效应规律的影响，将峰值电平压缩1.5 dB, 6 dB和12 dB分别作为阻塞干扰敏感判据进行试验研究。

3.2 双频临界干扰特性测试

基于不同的敏感判据与双频干扰频偏，测定受试雷达的单频、双频临界干扰场强。对于双频干扰频率的选择，首先要涉及受试雷达工作频带内与带外频率，以增加验证的可信性；其次，要防止双频干扰信号的3阶互调频率落入工作频带内造成额外干扰[16]；另外，若2阶互调差频频率(即两者频差)小于接收机末级混频器后低通滤波器带宽，则在某些情形下同样会造成阻塞干扰[17]，故双频干扰信号的频差要显著高于低通滤波器带宽。结合受试雷达零中频体制的特性，可选择干扰频偏为0 Hz,90 MHz与-150 MHz, 150 MHz的双频干扰信号进行试验。

为便于表示，将双频临界干扰场强组合(E1,E2)相对其单频临界干扰场强E10,E20进行归一化处理，并按场强有效值敏感双频电磁辐射效应模型式(6)计算得到双频电磁辐射阻塞效应指数R，结果如表1-表3所示。

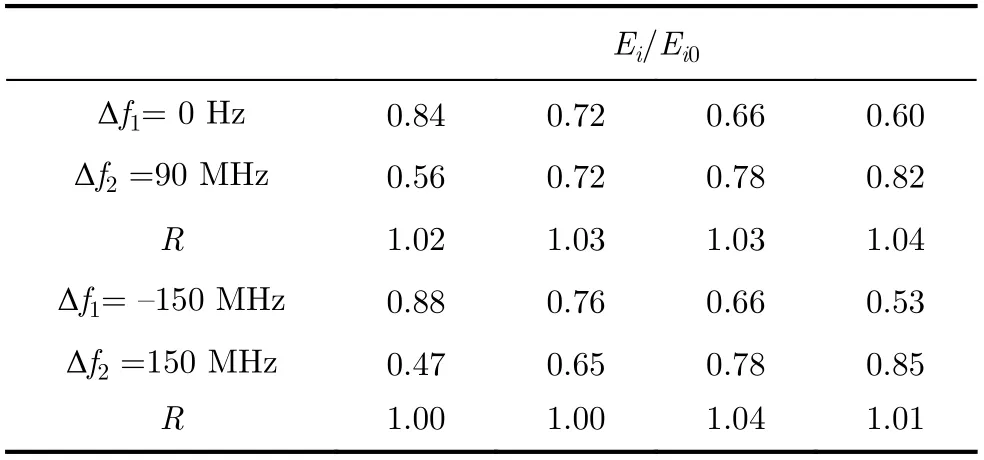
表1 以峰值电平压缩1.5 dB为敏感判据试验结果

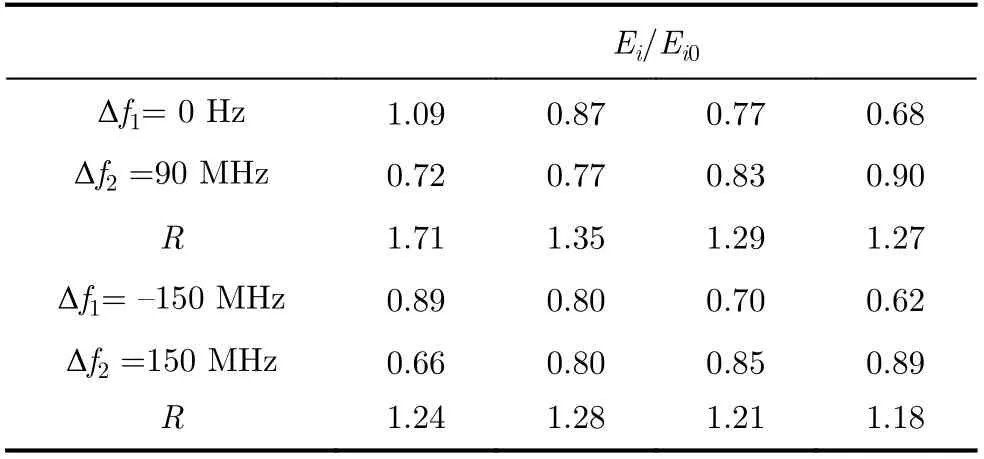
表2 以峰值电平压缩6 dB为敏感判据试验结果

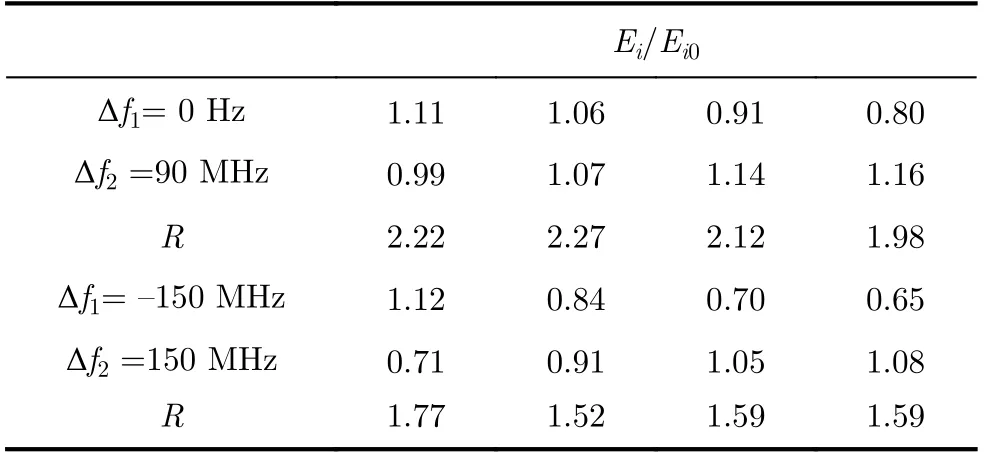
表3 以峰值电平压缩12 dB为敏感判据试验结果

表1是以峰值电平压缩1.5 dB为敏感判据的试验结果，双频临界干扰归一化场强组合均小于1，说明双频干扰信号对受试雷达造成有效干扰时，各干扰分量所需能量小于其单独作用；双频电磁辐射阻塞效应指数约为1，说明其符合有效值敏感双频电磁辐射效应模型，此时系统可由幂级数展开式1,3阶项来描述。表2、表3分别是以峰值电平压缩6 dB, 12 dB为敏感判据的试验结果，出现临界干扰时部分干扰分量归一化场强大于1，说明双频阻塞效应出现了明显的减弱现象，双频干扰信号反而削弱了干扰效果；双频阻塞效应指数均有所上升，高至1.51，采用有效值敏感双频电磁辐射效应模型评估其干扰效果误差明显增大。综合以上试验结果可以看出，当峰值电平压缩6 dB, 12 dB时，相较于压缩1.5 dB，系统非线性失真程度增大，幂级数展开式5阶项的作用不可忽略，导致出现双频钝感效应；若此时双频干扰信号场强满足效应指数R=1，则受试雷达实际上并未达到临界干扰状态。上述试验结果与第2节理论分析相符。

3.3 有效电平相同时单频、双频干扰效果对比

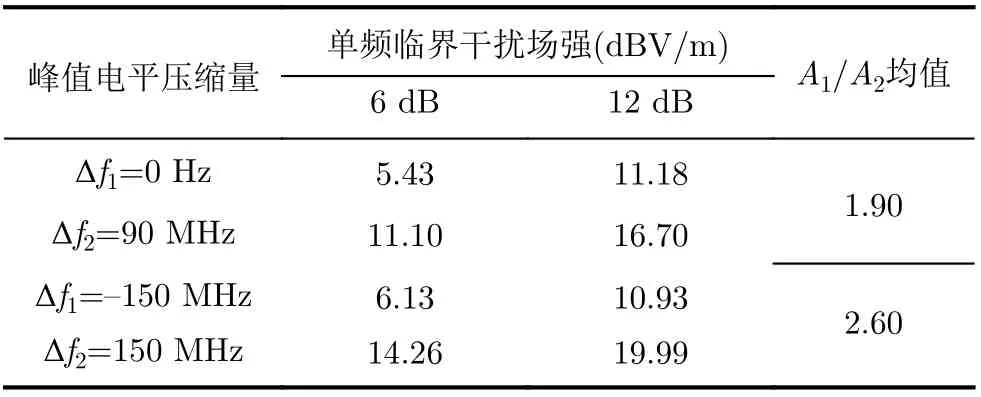
表4 单频临界干扰场强与选择系数比

对受试雷达同时施加双频干扰。选定不同的干扰频偏组合，结合选择系数比A1/A2调整两个干扰分量场强E1, E2，使双频干扰信号有效电平与表4中单频临界干扰有效电平相等，测量峰值电平压缩量。按照ΔU1,2=|A1E1−A2E2|计算双频干扰信号两分量的有效电平差，由于测试的目的仅在于分析规律，故可令A2=1 m进行计算。结果如表5、表6所示。

由表5、表6可知，当单频、双频干扰信号有效电平相等时，在双频干扰下峰值电平压缩量低于单频情形，双频干扰效果差于单频；双频干扰信号两个分量的有效电平越接近，峰值电平压缩量越小，干扰效果越差，受试雷达对双频干扰越钝感，与第2节理论分析相符。

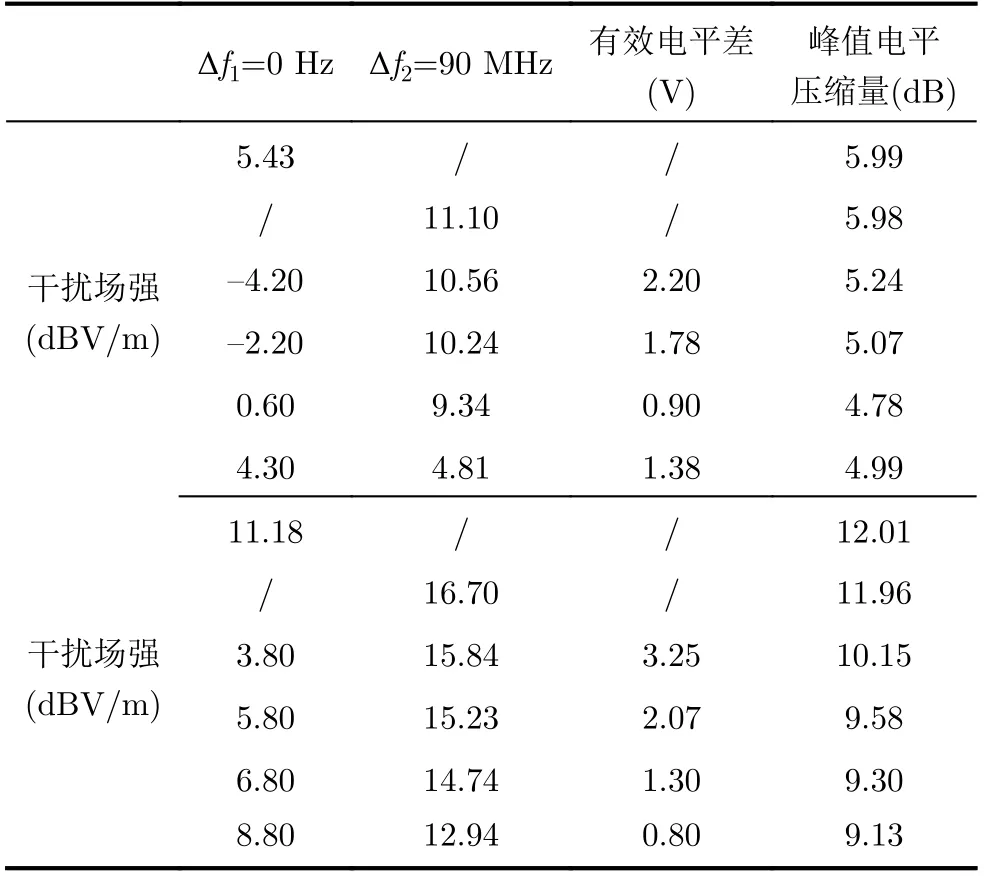
表5 频偏0 Hz, 90 MHz双频干扰试验结果

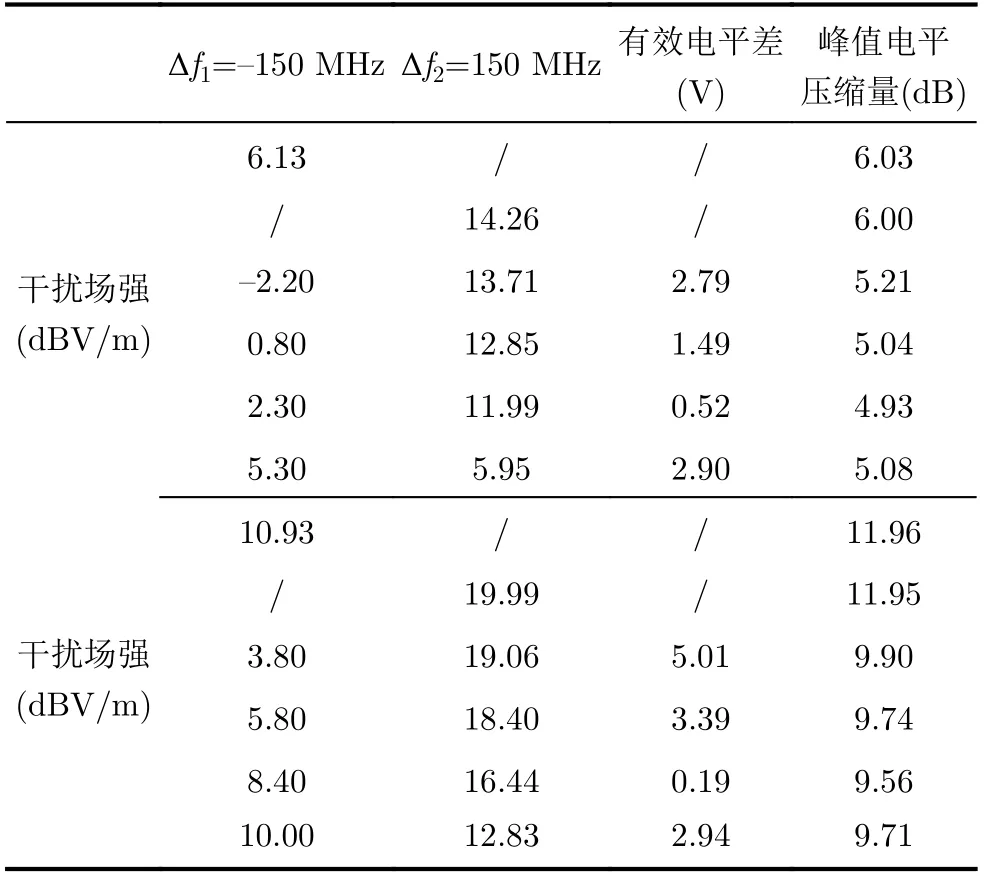
表6 频偏-150MHz, 150 MHz双频干扰试验结果

3.4 分量强度变化对干扰效果的影响

对受试雷达施加双频干扰。选定敏感判据，调整干扰分量1的场强E1，使受试雷达在其单独作用下处于临界干扰状态，在此基础上调整干扰分量2场强E2，记录峰值电平压缩量的变化，结果如图2所示。

从图2可以看出，当干扰分量1单独作用使峰值电平压缩12 dB时，随着干扰分量2的增强，峰值电平压缩量先下降后上升，即有用信号增益先上升而后下降。增益上升的现象与第2节规律分析相一致，其机理在于幂级数展开式的5阶项放大了有用信号；当干扰分量2增强到一定程度后，干扰分量1的作用可忽略，此时有用信号增益的变化与单频干扰类似[12]，随干扰分量2的增强而下降。当干扰分量1单独作用分别使得峰值电平压缩1.5 dB, 6 dB时，随着干扰分量2的增强，有用信号增益下降。其中，当峰值电平压缩6 dB时，根据前文分析，系统输入输出幂级数展开式的5阶项不可忽略，但是由于此时干扰分量1的强度相对较弱，3阶项仍处于主导地位，钝感现象不明显，有用信号增益的上升过程不明显，被试验误差掩盖。

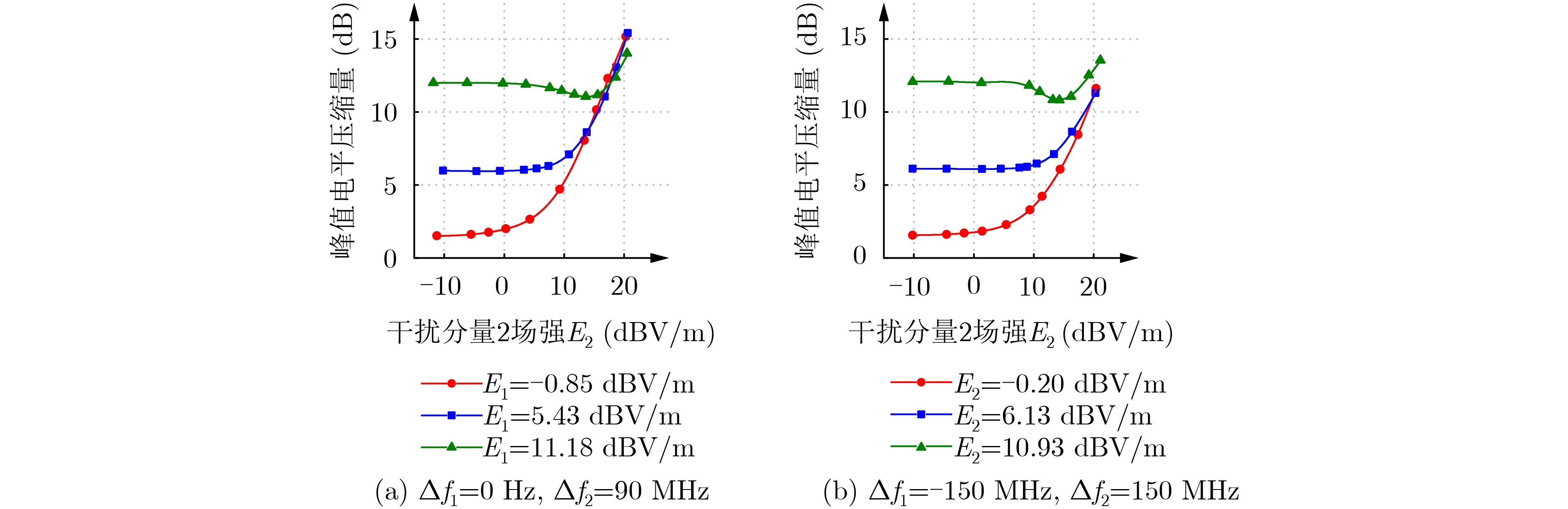
图2 峰值电平压缩量随干扰信号2场强的变化

4 结论

本文通过理论分析与试验验证，对有效值敏感型装备的双频钝感效应规律与作用机理进行了探究，得到结论如下：

(1)场强有效值敏感型装备的双频钝感现象是由幂级数展开式中5阶项引起的。当干扰信号较弱、系统非线性失真程度较低时，非线性系统的传递函数可由精确到3阶项的幂级数展开式来描述，单频、双频干扰信号临界干扰有效电平相等，有用信号增益决定于干扰信号场强有效值，此时不存在双频钝感现象；当干扰信号增强、系统非线性失真程度增加时，幂级数展开式的5阶项不可忽略，出现双频钝感现象。

(2)作为敏感判据的峰值电平压缩量越大，双频信号干扰效率下降越严重，甚至会出现双频临界干扰场强分量高于单频临界干扰场强的情况；当单频、双频干扰信号有效电平相等时，双频干扰效果差于单频，且两个干扰分量有效电平越接近，干扰效果越差。若在单频干扰基础上额外施加单频干扰，随着该单频干扰的增强，有用信号增益先增加后减弱。

(3)对于不同装备而言，需要基于不同敏感现象来选择具体的敏感判据，但敏感现象实质上是由有用信号增益压缩引起的。因此，尽管本文中以峰值电平压缩量作为敏感判据，但据此得到的相关结论完全可向其他情形推广。