基于NMPTS 模型的太阳黑子预测
2022-03-09马芳王鸿绪
马芳 王鸿绪
(1、沈阳工业大学,辽宁 沈阳 110870 2、海南热带海洋学院,海南 三亚 572022)
1 概述
太阳活动对人类、其他生物都有重大影响(Zeydin,et al.2019). Abdel-Rahman & Marzouk.(2018)应用的方法是一阶自回归模型AR(1)和改进的综合移动平均模型ARIMA(Autoregressive Integrated Moving Average Models)。经过九十多年的发展,建立于二世纪七十年代的ARIMA 模型是应用最广泛的回归分析方法之一,可以根据该时间序列的过去及现在值来预测其未来值(Li & Liu.2019)。本文在时间序列论域J 和差值论域H 上建立分式函数Ae(m,q,s)和次逆函数与预测函数Ke(m,q,s),提出并证明收敛定理,从而建立一个预测时间序列的新模型(A new model of a prediction for a time series,NMPTS)。
新预测模型NMPTS 和智能优选不动点算法,共同组成NMPTS 的预测理论。本文的主要改进有四点:a.直接应用“时间序列的数据”建立预测公式,这是提高模型预测精度的主要原因之一;b.应用演绎法和极限理论提出新模型NMPTS;c.把基于函数论和模糊控制算法(FTFCA)叫做NMPTS 的智能优选不动点的算法;d.提出“时间序列数据的差值”的概念,使得NMPTS 的基于函数论和模糊控制的建模(The function theory and a fuzzy control based the model,FTFCM)FTFCM1D1Ke不仅能够预测时间序列J 的训练阶段和测试阶段的数据,而且能够预测时间序列J 的未来阶段的数据。
新模型NMPTS 和智能优选不动点的算法,共同组成NMPTS 的预测理论。并用它对于太阳黑子(未来阶段)201908~201912 月的数量进行预测。与现有的AR(1)模型和ARIMA 模型比较,预测精度有较大提高。
2 NMPTS 的基本理论

其中自变量m∈(0,1],q∈(0,1],s∈(0,1]。Ae(m,q,s)叫做时间序列J 或NMPTS 的第e 个分数函数。Ke(m,q,s)叫做时间序列J 或NMPTS 第e 个分数函数Ae(m,q,s)对应的次逆函数或预测函数、预测公式、预测模型。
定义2 设时间序列论域为J={J1,J2,…,Jn}。第e-1 个差值的计算公式为

得到差值的论域为H={H1,H2,…,Hn-1}。
定理2 设时间序列论域为J={J1,J2,…,Jn},差值论域为H={H1,H2,…,Hn-1}。根据定理1 和定理2 能够证明:

定理3(NMPTS 的连续性定理)设时间序列论域为J={J1,J2,…,Jn},差值论域为H={H1,H2,…,Hn-1}。则
(1)(NMPTS 的分数函数Ae(m,q,s)的连续性定理)NMPTS 的分数函数Ae(m,q,s)是(0,1](0,1](0,1]上的连续函数;
(2)(NMPTS 的预测函数Ke(m,q,s)的连续性定理)NMPTS 的预测函数Ke(m,q,s)是(0,1](0,1](0,1]上的连续函数。
定理4(NMPTS 的收敛定理)设时间序列论域为J={J1,J2,…,Jn},差值论域为H={H1,H2,…,Hn-1}。对于任意取定的m∈(0,1],q∈(0,1],s∈(0,1]。固定q,当m→0,s→0 时,则:
(1)(NMPTS 的分数函数Ae(m,q,s)的收敛定理)NMPTS的分数函数Ae(m,q,s)是收敛的,并且第e 个NMPTS 的分数函数Ae(m,q,s)收敛于时间序列J 中第e 个元素的表达式q/Je(e=1,2,…,n);
(2)(NMPTS 的预测函数Ke(m,q,s)的收敛定理)NMPTS的预测函数Ke(m,q,s)是收敛的,并且第e 个NMPTS 的预测函数Ke(m,q,s)收敛于时间序列J 中第e 个元素Je(e=1,2,…,n)。
定义4 设时间序列论域为J={J1,J2,…,Jn},差值论域为H={H1,H2,…,Hn-1}。以任意点G(m,q,s)作为计算的起点,如果应用预测公式Ke(m,q,s)(e=1,2,…,n)预测时间序列J中的第e(e=1,2,…,n)个数据时,当所有得到的预测值Ke(m,q,s)(e=1,2,…,n)经过四舍五入的近似值等于J 中的第e(e=1,2,…,n)个数据Je时,则再多保留小数点后1~3位,此时得到的SE 和MSE 分别叫做准SE 和准MSE。并称准MSE 为不动点。此时得到的模型叫做实现NMPTS 中的建模,并记这个预测模型为基于函数论和模糊控制(FTFCM)的建模为FTFCM1D1Ke(m1,q,s1),或者NMPTS 中的建模FTFCM 11DK(em1,q,s1),或者时间序列J 中的建模FTFCM11DK(em1,q,s1)。
3 NMPTS 的智能优选不动点的算法
设时间序列论域为J={J1,J2,…,Jn},差值论域为H={H1,H2,…,Hn-1}。
(1)在时间序列J 的训练阶段,以任意点G(m,q,s)作为计算的起点,固定q,令m=s 逐渐减少,编程,搜索,用预测公式(2)进行计算,…,预测函数值Ke(m,q,s)的收敛定理保证:一定能得到不动点准MSE≈0,实现建模FTFCM1D1Ke(m1,q,s1)。
检验:如果在NMPTS 中的建模FTFCM1D1Ke(m1,q,s1)中把参数m1和s1继续减少。虽然MSE 可能继续减少,不是不动的,但是每个预测值Ke经过四舍五入都能等于观测值Je却是不动的。则确认FTFCM1D1Ke(m1,q,s1)是NMPTS 中的训练阶段的建模。
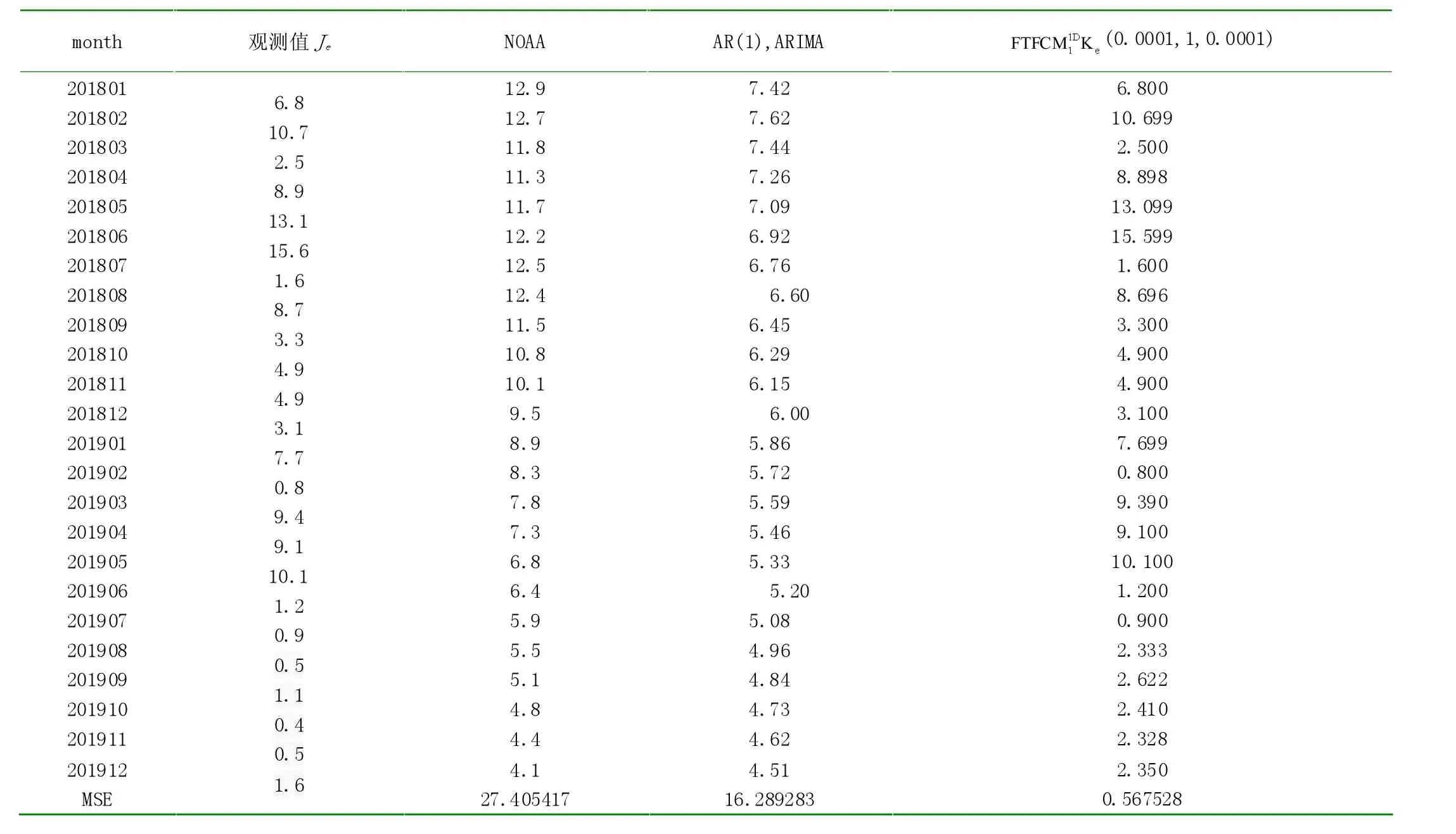
(2)在时间序列J 的测试阶段,应用NMPTS 中的建模FTFCM1D1Ke(m1,q,s1)计算时间序列J 中的测试阶段的数据。用公式(3)进行计算。如果得到不动点准MSE≈0,那么NMPTS 中的建模FTFCM1D1Ke(m1,q,s1)为时间序列的训练阶段和测试阶段的建模;否则应用预测模型Ke(m2,q,s2)(应当m2 检验:如果在NMPTS 中的建模FTFCM1D1Ke(m3,q,s3)中把参数m3和s3继续减少,虽然MSE 可能继续减少,不是不动的,但是每个预测值Ke经过四舍五入都能等于观测值Je却是不动的。则确认FTFCM1D1Ke(m3,q,s3)是NMPTS 中的测试阶段的建模。并进一步确认FTFCM1D1Ke(m3,q,s3)是NMPTS 中的训练阶段和测试阶段的建模。它是计算NMPTS中的未来阶段数据的预测模型。 (3)在时间序列J 的未来阶段,应用NMPTS 中的建模FTFCM1D1Ke(m3,q,s3)和NMPTS 的智能搜索优选不动点算法(双样本求法),及预测公式(6)以及虚拟预测值公式(7)进行计算。 ①在预测时间序列Y={Y1,Y2,…,Yn}的未来阶段数据Hn+1时,在虚拟预测值公式 中,取σ=1,计算时间序列J 的未来阶段第n+1 个数值Jn+1的虚拟预测值K*n+1。 ②使用测试阶段得到的Kn,要把Kn也看成未来阶段的数据,并把Kn和Kn+1作为一组未来阶段的数据进行预测计算,求出未来阶段预测值Kn+1的数据。计算出Kn和Kn+1。 ③计算的过程分别定义为:启动计算(微0调计算),微调计算(微1调计算),微微调计算(微2调计算),……。对应的(微g 调计算)(g=1,2,…)的步长根据参数的大小,自行设计。例如可分别取1×10-h,为微h调计算的步长。计算的次数为第1 次计算,第2 次计算,…。计算预测值时,要用预测公式(3)进行计算。类似地可计算时间序列Y 的未来阶段的第n+2,n+3,…个数据的预测值。 ④在具体计算时,微i调计算的使用规则是: ……… 第j 轮微i调计算。第j+2 次计算。如果第j+1 次计算得知MSEj+1比第j 次计算得到的MSEj小,则继续微i调计算;如果大,出现拐点,则退回到第j 次计算,改为微i+1调计算,继续计算。 ⑤计算到(第k 轮微m调计算)第u 次计算得到的MSEu,如果与前面的(第p 轮微s调计算)第q 次计算得到的MSEq相等,则得到不动点准MSEu=MSEq,此时对应的预测值Kn+1就是本方法求出的时间序列J 的未来的第n+1 个数据的预测值。不动点准MSE 是各轮各微各次计算中最小的。 ⑥检验。如果继续进行“加轮加微加次”计算,“不动点准MSEn+1”不变,而且“预测值Kn+1”也不变。 ⑦在预测时间序J 的未来阶段数据Kn+2时,要把Kn+1看成未来阶段数据,并使用已经计算出的Kn+1的数据,把Kn+1和Kn+2作为一组未来阶段数据进行预测计算,类似于①~⑥各步骤,得到“不动点准MSEn+2”,以及“预测值Kn+2”。 类似地可计算时间序列J 的未来阶段的预测值Kn+3,Kn+4,…,各数据的预测值。 把太阳黑子201601~201712 月的数据作为训练阶段,201801~201907 月的数据作为测试阶段阶段,201908~201912 月的数据作为未来阶段,应用NMPTS 的预测理论和NMPTS 的智能优选不动点法进行预测,预测结果与各模型预测结果比较如表1 所示。 表1 各模型预测太阳黑子测试阶段和未来阶段的数据比较 表2 展示了FTFCM1D1Ke(0.0001,1,0.0001)的预测数据,约比Abdel-Rahman & Marzouk(2018)应用AR(1)&ARIMA prediction 的预测精度高4 倍以上;比Abdel-Rahman& Marzouk(2018)列举出NOAA prediction 的预测精度高4倍以上。 表2 各模型预测太阳黑子的数据的比较 提出NFMTS 的预测理论。在太阳黑子的数值试验中,相比Abdel-Rahman & Marzouk(2018)应用AR(1)& ARIMA模型以及Abdel-Rahman & Marzouk(2018)提供的NOAA使用的模型预测太阳黑子的测试阶段和未来阶段201801~201912 的月数据,NFMTS 的建模FTFCM1D1Ke(0.0001,1,0.0001)的预测精度都有较大幅度的改善。表2 显示:对于预测太阳黑子的未来阶段201908~201912 的月数据,NMPTS 的建模FTFCM1D1Ke(0.0001,1,0.0001)的预测数据也有一定的优势。所以NFMTS 的预测理论对于太阳黑子数量的时间序列,补充了一种新的预测方法;对于一般的时间序列,提供了新的预测方法。
4 数值实验-太阳黑子的预测研究

5 结论
