基于谐波调谐的双频高效功率放大器设计

张少倩

（天津大学，天津 300072）

引 言

随着无线通信技术的发展，通信方式逐渐由传统的单频点通信转变为多模多带通信，这就要求基站前端能处理不同通信标准和频段的信号. 作为发射机中的关键模块，功放也需要具备放大多个频段信号的能力[1]. 基于此需求，双频功放的研究逐渐兴起.

另一方面，功放也是发射机中最耗能的模块. 为了降低系统功耗，必须提高功放的效率. 学者们已经提出多种双频高效功放的设计方案. 文献[2-3]分别提出了一种新型双频阻抗变换器结构，均可以实现任意两个频率下基波阻抗的匹配. 然而，由于设计过程中忽略了谐波阻抗的影响，功放的实际效率并不高. 考虑谐波阻抗可以进一步提高功放的效率，例如E类功放[4-5]、F类功放[6-8]和谐波调谐类功放[9-10]的设计. 其中，谐波调谐类功放具有不受工作频率的限制和对阻抗条件要求较低等优点，受到了广泛关注. 文献[9]通过调谐两个频点的二次谐波和三次谐波阻抗来实现高效功放，但由于使用较多的开路枝节，电路损耗增大，结构更为复杂，而且两个频点的基波匹配电路缺少解析解. 文献[10]通过控制更少的谐波阻抗进一步简化电路，但是其基波匹配电路的匹配效果并不理想，导致两个频率下的性能差异较大.

为了解决上述问题，本文提出一种新型双频高效功放的设计方法. 将一种新的双频匹配电路应用于基波阻抗匹配和二次谐波阻抗匹配. 由于仅控制二次谐波阻抗，极大地简化了谐波控制电路，又实现了相对较高的效率. 此外，通过理论推导获得了基波匹配电路的解析解，使得该匹配结构易于实现. 本文提出的双频功放可以在较高的两个频率下并行工作.为了验证方法的可行性，设计了一款工作在1.9/2.6 GHz的功放. 测试结果表明，两个频率下该功放均具有67%以上的功率附加效率(power added efficiency, PAE)和40 dBm左右的输出功率.

1 高效功放设计原理

图1所示为功放的结构简图，主要由晶体管、输入匹配电路、RC稳定电路、输出匹配电路、栅极偏置电路和漏极偏置电路组成. 输入和输出匹配电路的作用是将晶体管的最佳源/负载阻抗匹配至50 Ω，该无源电路会产生一定的功率损耗Ploss；偏置电路的作用是为晶体管提供合适的供电电压，Psup表示直流电压源所产生的直流功率.

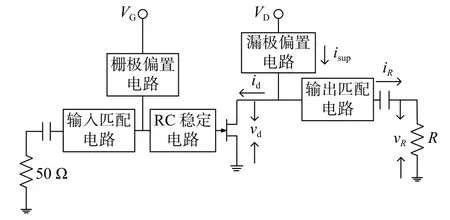
图1 功放的结构简图Fig. 1 Structure diagram of power amplifier

定义晶体管漏极电压为vd， 漏极电流为id，传输到晶体管的功率为Pd， 传输到负载R的功率为PR. 记功率消耗为正值，功率产生为负值. 根据能量守恒原理可得[11]：

式中，k表示第k次谐波分量.

当k=1时，直流电压源在基波频率下无功率产生，即

则功放的功率关系可表示为

式中，PR[1]表示负载上获得的有用功率，即输出功率Pout.

晶体管是功放中唯一的非线性器件，这说明除直流电源提供的直流功率外所有功率均来自晶体管.所以，

但是晶体管并非功率源，传输到它的总功率为非负值，即

联立式(3)至(5)可得

式中，传输到晶体管的功率Pd可 用漏极电压vd和电流id来表示. 漏极电压vd和 漏极电流id的傅里叶级数表达式为：

式中：VDC表 示漏极电压的直流分量；vd[k]表示第k次谐波的电压幅度； αk表示第k次谐波电压的相位；IDC表 示漏极电流的直流分量；id[k]表示第k次谐波的电流幅度； βk表 示第k次谐波的电流相位；θ表示归一化时间变量. 因此，传输到晶体管的功率Pd为：

根据式(9)和(10)，可以将式(6)写为

不等式右边第一项表示直流功率，第二项表示谐波功率，第三项表示匹配电路的功率损耗. 式(11)表明，输出功率最大不超过直流功率减去谐波消耗功率，即谐波功率损耗的产生降低了功放的效率. 要设计高效功放，需要避免谐波功率产生，即使不等式右边第二项为0. 当第k次谐波的电压幅度或者电流幅度为0时，谐波功率一定为0. 当第k次谐波的电压和电流相位差90°时，谐波功率也为0. 电压幅度为0对应的阻抗条件为短路，电流幅度为0对应的阻抗条件为开路，电压和电流相位差90°对应的阻抗条件为纯电抗.

由于高频下晶体管寄生参数的影响变大，理想的阻抗开路或短路难以实现，本次设计高效功放采取第三种措施，即通过谐波调谐控制谐波阻抗为纯电抗. 因控制谐波次数越高，电路越复杂. 为了简化电路，本设计仅控制对效率提升作用最大的二次谐波.

2 双频高效功放的设计方法

双频输出匹配电路是双频功放的重要组成部分.图2所示为本文设计提出的新型输出匹配电路原理图，包含双频谐波控制电路和双频基波匹配电路两部分.

图2 新型输出匹配电路原理图Fig. 2 Schematic of the novel output matching circuit

2.1 双频谐波控制电路设计

基于第1节对高效功放阻抗条件的分析，本文提出一种新型谐波控制电路，通过四分之一波长开路枝节在信号路径产生谐波阻抗零点，再利用调谐线调节两个谐波频率下的电抗值，使其处于高效区域.

设计的谐波控制电路由串联传输线T1和并联开路传输线T2、T3组成. 设置传输线T2的电长度在2f1频率下为90°，使A点处2f1谐波阻抗为0. 设置传输线T3的电长度在2f2频率下为90°，使A点处2f2谐波阻抗为0. 根据负载传输线理论，调节传输线T1的特征阻抗Z1和电长度 θ1，可以将A点处2f1和2f2的短路状态匹配到晶体管的最佳二次谐波阻抗. 匹配原理如下：

式中：ZL(2f1)、ZL(2f2)表示晶体管在两个频率下的最优二次谐波阻抗，实际设计中通过对晶体管进行谐波负载牵引得到；m=f2/f1表示两个工作频率的比值.求解式(12)和(13)，即可得到传输线T1的特征阻抗和电长度.

2.2 双频基波匹配电路设计

由2.1节可知，A点处两个所需频率的二次谐波均短路. 所以，A点之后的基波匹配电路不会影响A点前的谐波控制电路. 此外，在添加谐波控制电路之后，晶体管的最佳基波阻抗会发生变化. 设计匹配电路时，需要将A点后两个频率的基波阻抗匹配至50 Ω.的复阻抗ZA(f1)、ZA(f2)转 化为一对共轭复导纳YB(f1)=GB−jBB、YB(f2)=GB+jBB；第二步，利用传输线T5抵消两个频率下YB的虚部 ∓BB；最后，利用传输线T6和T7完成双频实阻抗之间的匹配.

本设计提出的双频基波匹配电路由串联传输线T4、T6、T7和并联开路传输线T5组成. 其匹配过程共分为三步：第一步，利用传输线T4将A点两个频率下

2.2.1 传输线T4的设计

结合晶体管的最佳基波阻抗ZL(f1)、ZL(f2)和谐波控制电路的参数，可以计算得出A点的基波阻抗ZA(f1)=R1+jX1、ZA(f2)=R2+jX2. 文献[12]表明，传输线T4可以将两个互不相关的阻抗ZA转化为一对共轭复阻抗，传输线的特征阻抗Z4和 电长度 θ4需满足：

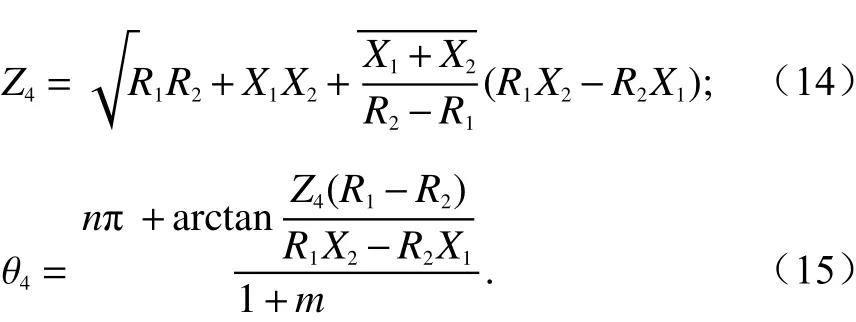
2.2.2 传输线T5的设计

参考面BB′的 共轭复导纳YB(f1)=GB−jBB、YB(f2)=GB+jBB可以根据终端加载传输线的输入阻抗公式计算得出. 开路枝节T5的作用是抵消两个频率下的电纳部分 ∓jBB. 由于在一个节点处并联电路的导纳为求和，所以T5枝节在两个频率下的输入阻抗需满足±jBB，即：

开路枝节T5的电长度 θ5和 特征阻抗Z5通过求解式(16)和(17)得出：

2.2.3 传输线T6和T7的设计

经过传输线T4和T5的阻抗变换，可以确定B点两个频率的阻抗均为R=1/GB. 构造串联传输线T6和T7为双频四分之一波长阻抗变换器，将实阻抗R在 两个频率下匹配至负载RL. 传输线T6和T7的特征阻抗和电长度需满足[13]：

通过计算传输线T4、T5、T6和T7的参数，完成了双频下复阻抗到实阻抗的变换. 将该结构应用于双频功放的基波匹配电路，不仅可以简化求解过程，还可以精确地匹配基波阻抗.

3 双频高效功放的仿真与测试

为了验证本文设计的可实施性，加工了一款工作在1.9/2.6 GHz的双频高效放大器. 功放的有源器件选用cree公司的CGH40010 GaN HEMT晶体管.在ADS中对晶体管进行LoadPull仿真，获得封装面的最优基波负载阻抗和二次谐波负载阻抗；SourcePull仿真获得晶体管的最优源阻抗. 最优负载阻抗和最优源阻抗在史密斯圆图上的位置如图3所示.

图3 最优阻抗和匹配电路阻抗在史密斯圆图上的位置分布Fig. 3 The optimal impedances and the impedances of the matching circuit on the Smith chart

根据第2节提出的匹配理论设计功放的输入和输出匹配电路，图3所示为匹配电路的电磁仿真结果. 可以看出：基波负载阻抗和源阻抗均实现了良好的匹配；二次谐波负载阻抗和最优源阻抗差异较大，但仍处在高效率区域.

功放完整原理图如图4所示. 输入端添加RC稳定电路，保证功放在工作频带范围内绝对稳定. 考虑到输入端谐波对电路性能影响较小，本设计忽略输入谐波.

图4 本文提出的功放原理图Fig. 4 Schematic of the proposed power amplifier

图5所示为晶体管在1.9/2.6 GHz的漏极电压和电流波形仿真结果. 由图5可知，漏极电压和电流的波形在时域上重叠面积较小. 当漏极电压最大时漏极电流为0，当漏极电流最大时漏极电压为0，符合高效功放的设计需求.

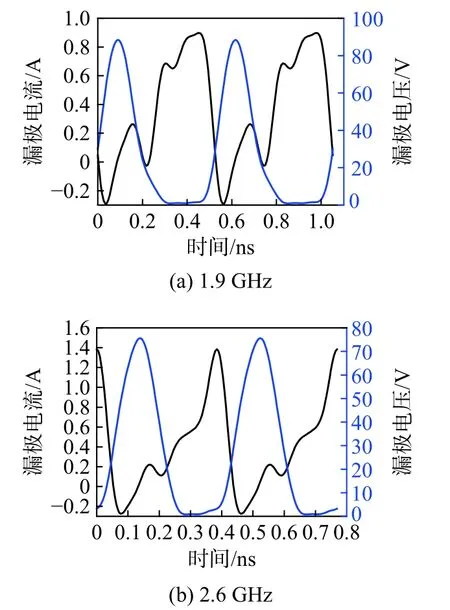
图5 晶体管在1.9/2.6 GHz处漏极电压和电流波形仿真结果Fig. 5 Simulation result of the drain voltage and current waveforms of the transistor at 19/2.6 GHz

功放实物如图6所示. 加工介质基板选择厚度为0.787 mm，介电常数为3.66的罗杰斯4350B. 漏极偏置电压设置为28 V，栅极偏置电压设置为−2.85 V，确保漏极静态电流IDS=200 mA，从而使功放在AB类偏置状态下工作. 利用单音连续波对功放在两个工作频率1.9/2.6 GHz处进行大信号性能测试，输入功率从10 dBm调节到30 dBm，PAE、输出功率和增益随输入功率变化的曲线如图7所示. 由图7可知，功放在两个频点的实测峰值PAE分别为72.5%/67.8%，最大输出功率分别为39.8/40.03 dBm，大信号增益均为10.7 dB. 从图7也可以看到，由于晶体管模型和实际器件之间存在差异，以及工厂加工和元器件焊接存在误差，实测性能比仿真性能略有下降.

图6 功放加工实物图Fig. 6 Photograph of the designed PA

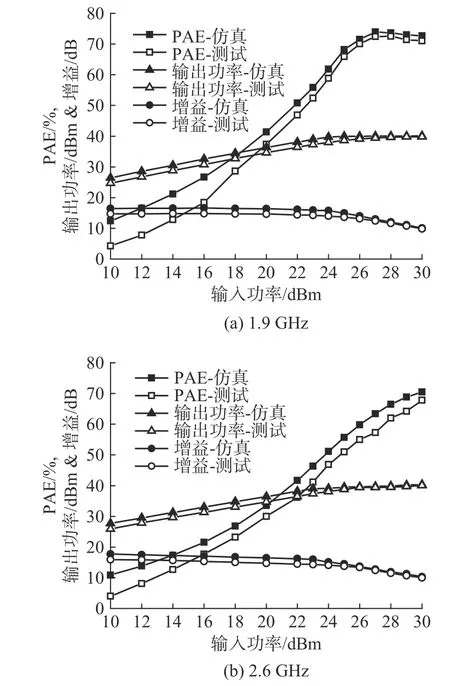
图7 PAE、输出功率和增益随输入功率变化曲线Fig. 7 PAE, output power and gain vs. the input power

固定输入功率为29 dBm，扫描信号频率范围为1.7～2.7 GHz. 测试功放的大信号性能随频率变化的特性，测试结果和仿真结果如图8所示. 可以看出，PAE在1.9 GHz和2.6 GHz处出现局部最大值，表现出明显的双频特性.

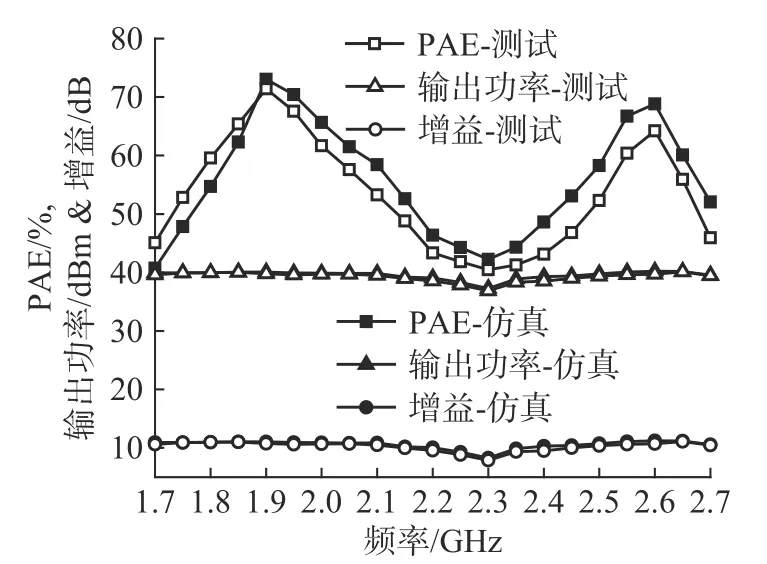
图8 PAE、输出功率和增益随频率变化曲线Fig. 8 PAE, output power and gain vs. frequencies

表1对本文设计与国内外已发表文献进行了指标对比. 由表1可知，本文提出的双频功放性能优异，在同类设计中处于较高水平.

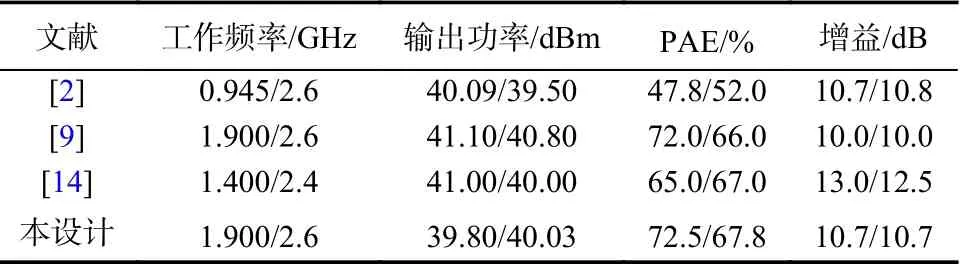
表1 本设计与其他双频功放指标对比Tab. 1 Comparison between this design and other dual-band power amplifiers

4 结 论

本文提出了一种并发双频高效功放的设计方法.通过对功放高效工作的原理进行分析，得出功放的谐波阻抗条件. 提出了一种新型匹配电路，实现基波和二次谐波阻抗精确匹配的同时，降低了设计难度和电路复杂度. 加工了一款工作在1.9/2.6 GHz的功放来验证方法的可行性. 与近年文献相比之间，设计的功放具有较高的效率和输出功率，解决了双频带功放不能在两个频带同时工作和效率不高的问题.由于单端放大器无法高效地放大高峰均功率比的通信信号，后续研究将着重于双频高效Doherty功放的设计.