基于1/3倍频程与传递函数方法的地铁轨道振动规律实验对比研究
2022-03-09尹华拓曾志平黄旭东吴志鹏
尹华拓,袁 宇,曾志平,黄旭东,吴志鹏
(1.广州地铁设计研究院股份有限公司,广州 510010;2.南昌大学 信息工程学院,南昌 330031; 3.中南大学 土木工程学院,长沙 410075)
地铁作为城市轨道交通工具的一种,具有运输能力大、速度快且高效的优点。随着我国城市化不断发展,城市人口不断增加,城市拥堵问题显得日益严重,而地铁能够有效缓解交通拥堵问题,方便人们出行,所以目前国内各个城市相继建设开通新的地铁线路[1–2]。但是,由于地铁功能的需求,其线路一般穿过密集商业区、科技园区、风景区、人流汇集区等,其中古建筑、各种精密仪器等对振动极其敏感,因此研究地铁运营时列车产生的振动传递具有十分重要的现实意义[3–5]。
在现有的无砟轨道振动测试研究中,常常利用加速度传感器直接对钢轨、轨道板、隧道壁的振动进行测试,并进行时域与加速度分析。例如,曾志平等[6]采用落轴冲击的方式,针对改进型弹性支撑块式无砟轨道结构的振动规律进行了研究;夏放等[7]以不同的计权方式对地铁线路不同轨道结构的车内外振动噪声进行了测试和对比;刘鹏辉等[8]对地铁隧道内的不同轨道结构的振动进行了分析,采用的分析方式为Z 计权、时域分析和源强分析;陈卓等[9]以功率谱分析和分频振级的角度,对两种弹性支撑块式无砟轨道的结构进行了对比研究;Wang等[10]以橡胶隔振垫浮置板轨道为研究对象,以频域和时域的角度分析了隧道壁竖向振动特性,并与普通轨道进行了比较;Jiang等[11]以道岔区浮置板轨道为研究对象,分析了道岔区采用浮置板轨道的减振效果。可见,以往的研究主要从加速度时域和频域分析的角度对其分析,很少从传递函数的角度进行考虑,但是在现有的振动领域研究中,振动传递函数应用广泛,在对减振道床的振动性能评估时却鲜有相关研究文献。
在对地铁轨道进行振动测试时,为了规范不同城市区域及不同类型建筑对于振动的要求,国内制定了各类环境振动及建筑振动标准,其主要分为居住环境振动水平控制标准和结构振动水平控制标准两类[12]。现有大部分文献采用了居住环境振动水平的评价方式,依托规范为《城市区域环境振动标准》[13]和《城市区域环境振动测量方法》[14],评价指标为Z 振级及累计百分Z 振级。同时,现有文献没有形成统一规范的地铁振动测试评价指标,对于当前地铁振动环境影响评价仍然主要参照声环境“4a 类(即交通干线两侧)功能区”评价[15]的评价方式,在科学性和合规性方面存在瑕疵。鉴于此,本文提出1/3倍频程分析与传递函数分析相结合的地铁轨道振动分析方法,以期对现有地铁振动测试评价方法进行完善。
1 振动分析方法
1.1 1/3倍频程分析
常规的倍频程方法具有尺度的相对性,即通过一系列频率点以及附近频带内信号的平均幅值共同构成倍频程谱[16]。其中,频率点成为中心频率fc,其定义的附近存在的频带皆处于上限频率f1以及下限频率fm之间,其中1/3倍频程分析法是一种能够对振动进行频域分析的方法,在机械振动领域有着广泛应用,国际电工委员会对1/3倍频程的中心频率进行了建议[17]:
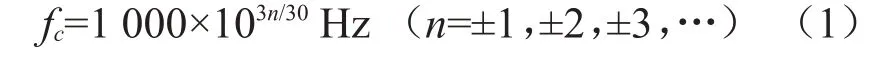
因此,根据我国《城市区域环境振动标准》[13]和《城市区域环境振动测量方法》[14],在对地铁轨道振动进行1/3 倍频程分析时,应该采用的中心频率为1、1.25、1.6、2、2.5、3.15、4、5、6.3、8、10、12.5、16、20、25、31.5、40、50、63、80、100、125、160、200、250、315、400、500、630、800、1 000,共31 个分析点[18–19]。可见,每隔3 个中心频率,频率值增加一倍。1/3 倍频程的上、下限频率以及中心频率之间的关系为:

1/3频程带宽为:

本文在对地铁普通整体道床以及减振道床进行研究时,首先采用加速度传感器测出研究对象的加速度时域数据,然后利用快速傅里叶变换计算出功、幅值谱,进而计算每一个中心频率的带宽内的平均值,最后得出所测地铁轨道的1/3倍频程的频谱图。
1.2 传递函数分析
传递函数法是一种适用于多自由度系统振动规律传递的方法[20],其基本的计算方法为:在零初始条件下,分别计算线性定常系统输出量以及输入量的拉氏变化,两者的比值即为该系统的传递函数[21],即:
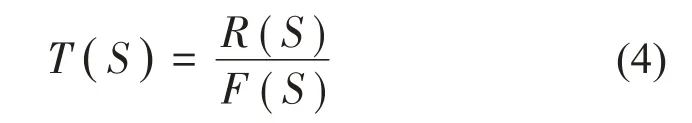
式中:T(S)为该系统的传递函数,R(S)和F(S)分别为输出量和输入量的拉氏式变换,在计算时分别采用钢轨、道床与隧道壁的加速度测试数据进行拉式变换,并对两者对应频率的范围的拉氏变换结果进行传递函数的处理分析。
在对地铁轨道的振动传递规律进行分析时,由于振动依次经过钢轨、道床、隧道,并最终作用于隧道周围土体,在对地铁轨道的振动传递规律进行分析时,其重点在于钢轨与道床、道床与隧道壁之间的传递。因此本文在进行研究时,重点对上述两类传递情况进行分析。
1.3 方法评价及意义
在对轨道振动响应进行分析时,目前多采用时域和频域分析方法,进而对比不同频率下的轨道振动情况。但是随着轨道交通的迅速发展,对地铁轨道振动的控制的要求不断提高,尤其是对列车振动传递规律的影响更加重视。在当前进行地铁轨道减振设计时,往往缺乏对地铁振动传递规律的研究,同时也十分缺乏相关的技术标准。
因此,本文通过引入传递函数方法,并利用同一测点的测试数据分别进行地铁轨道的1/3 倍频程分析以及传递函数分析,通过实际测试的数据对上述两种方法进行验证,以证实两种方法的适用性,尤其对传递函数法在评估轨道结构振动传递时的优势进行了特别阐述,以期为相关工程设计评价提供理论依据。
2 地铁轨道振动测试方案
通过对广州地铁某线路进行实车运行下的现场振动测试,测试了普通整体道床以及减振道床的钢轨、道床、隧道壁的振动加速度,用于对两种道床进行1/3倍频程分析和振动传递函数分析。
2.1 测点仪器与布置
测试仪器主要包括:动态数据采集仪、电脑、以及加速度传感器。测试断面分别为普通整体道床和减振道床两个隧道截面,所述隧道截面列车设计速度相同,且均为单洞单线圆形截面。所述测试断面的曲线半径、线路坡度以及列车行车速度对比如表1所示,隧道截面内加速度测点布置如图1所示。

表1 测试断面简况对比
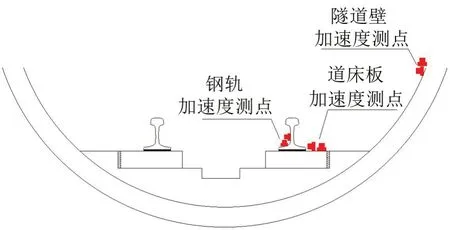
图1 测点布置示意图
2.2 测试的方法与步骤
首先对测试断面进行选定,再对钢轨、道床、隧道壁的测点进行了初步确定,在完成铁片粘贴后对测点进行传感器的布置操作。由于列车通过测试断面时,钢轨、道床以及隧道壁的振动大小不同,所以采用不同量程的加速度传感器进行测量。本次测试中钢轨采用500 g 量程的LC 压电式传感器,如图2所示;道床上采用50 g 量程的LC 压电式传感器,如图3所示;隧道壁采用2 g量程的LC压电传感器,如图4所示。通过对钢轨、道床、隧道壁振动加速度数据的采集,进而用于后续对三者振动特性的分析。

图3 道床测点布置

图4 隧道壁测点布置
3 地铁轨道振动测试数据分析
3.1 1/3倍频程对比分析
将普通整体道床和减振道床的钢轨、道床、隧道壁振动加速度采用1/3倍频程方法进行对比分析,结果如图5至图7所示。
(一)钢轨振动
如图5所示。对于钢轨垂向振动加速度级,减振道床在1 Hz~200 Hz的范围内略大于普通整体道床,在200 Hz~1 000 Hz 的范围内,两者无明显差异。对于钢轨横向振动加速度级,减振道床在1 Hz~25 Hz 的低频范围内略大于普通整体道床,而在25 Hz~1 000 Hz 的范围内基本无明显差异。此现象的原因在于整体道床的下部与基础为刚性连接,道床板整体约束较多,因此当道床板质量以及受到列车激励作用相同时,普通整体道床钢轨的振动响应将会略小于减振道床。

图5 钢轨加速度级
(二)道床振动
如图6所示。对于道床振动加速度级,无论垂向振动还是横向振动,减振道床的加速度级都要明显大于普通整体道床。

图6 道床加速度级
对于垂向振动,减振道床在0~1 000 Hz的范围内比普通整体道床大8.3 dB~36 dB。对于横向振动,减振道床在0~1 000 Hz的范围内与普通整体道床相差-2 dB~32 dB。
此现象的原因在于整体道床的下部与基础为刚性连接,道床板整体的约束较多,因此当道床板质量以及受到列车激励作用相同时,普通整体道床的道床板振动响应将会略小于减振道床。
(三)隧道壁振动分析
如图7所示。对于隧道壁垂向加速度级,普通整体道床在1 Hz~63 Hz以及80 Hz~1 000 Hz的范围内比减振道床大,而在63 Hz~80 Hz的范围内,普通整体道床比减振道床小。

图7 隧道壁加速度级
对于隧道壁横向加速度级,普通整体道床在1 Hz~31.5 Hz 的范围内与减振道床相差不大,在40Hz~80 Hz以及160 Hz~1 000 Hz的范围内,普通整体道床要大于减振道床,而在80 Hz~160 Hz的范围内,普通整体道床要小于减振道床,表明减振道床对于隧道壁横向振动在高频段减振明显。
此现象的原因在于减振道床的减振垫层将列车的振动能量通过自身的隔振作用进行了消耗,因此传递至隧道壁时,减振道床地段的隧道壁的振动响应普遍低于普通整体道床。但是由于减振道床主要耗散列车竖向的振动能量,因此水平方向的隔振效果有限。
3.2 传递函数对比分析
将普通整体道床和减振道床的钢轨、道床、隧道壁的垂向以及横向的振动加速度采用振动传递函数方法进行处理,其分析结果如图8至图11所示。
3.2.1 垂向振动传递
(一)普通整体道床
如图8所示。对于普通整体道床,垂向振动由钢轨至道床的传递过程中出现了3个主要传递函数峰值点,说明从钢轨传播至道床的垂向振动频率主要集中在200 Hz、450 Hz 以及700 Hz 左右,其中在700 Hz左右的振动传递率最大。由道床至隧道壁的垂向振动传递频率主要集中于250 Hz、500 Hz 以及700 Hz左右,其中在700 Hz左右的振动传递明显大于其他频段。
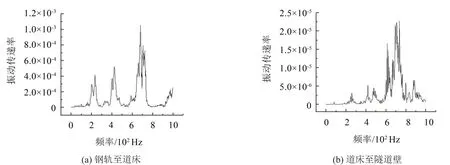
图8 普通整体道床垂向振动传递函数
(二)减振道床
如图9所示。由钢轨至道床的垂向振动传递过程在0~1 000 Hz范围内均有发生,其中在300 Hz左右的频率处传递率最大。由道床至隧道壁的垂向振动传递过程主要集中于100 Hz、700 Hz 两个频率点左右,其他的频率范围垂向振动传递率相对较小。

图9 减振道床垂向振动传递函数
将普通整体道床与减振道床的振动传递函数进行对比,对于钢轨至道床的垂向振动传递,普通整体道床的传递函数最大值为1.1×10-3,减振道床的传递函数最大值为2.7×10-2,说明普通整体道床的钢轨至道床的垂向振动传递效应更明显;普通整体道床钢轨至道床的垂向振动传递更集中于450 Hz 和700 Hz的高频段,而减振道床钢轨至道床的垂向振动传递主要集中于300 Hz的较低频段。
对于道床至隧道壁的垂向振动传递,普通整体道床的传递函数最大值为2.2×10-5,减振道床的传递函数最大值为1.2×10-5,说明减振道床的道床至隧道壁的垂向振动传递效应更明显;两种道床均在700 Hz 左右的频率处显示出道床至隧道壁的最大垂向传递效应。
3.2.2 横向振动传递
(一)普通整体道床
如图10所示,普通整体道床的横向振动由钢轨至道床传递在0~1 000 Hz范围内均有发生,同时振动传递函数出现多个峰值,且在600 Hz处横向振动传递率最大。横向振动由道床至隧道壁传递在0~1 000 Hz 范围内同样出现多个峰值,其中600 Hz 处的横向振动传递率最大。

图10 普通整体道床横向振动传递函数
(二)减振道床
如图11所示,减振道床横向振动由钢轨至道床的传递在0~1 000 Hz 的范围内均有发生,其中在800 Hz左右传递率最大。减振道床横向振动由道床至隧道壁的传递频率主要集中于350 Hz、550 Hz 和700 Hz左右,其中在700 Hz左右传递率最大。

图11 减振道床横向振动传递函数
普通整体道床与减振道床相比,对于钢轨至道床的横向振动传递率,普通整体道床的传递函数率最大值为1.1×10-4,减振道床的传递函数率最大值为3.0×10-4,说明普通整体道床的横向振动衰减较减振道床更明显,且减振道床由钢轨至道床的横向振动传播在0~1 000 Hz 范围内更广泛。对于道床至隧道壁的横向振动传递,普通整体道床的传递函数最大值为4.5×10-6,减振道床的传递函数最大值为2.7×10-5;普通整体道床的道床至隧道壁横向振动传递函数在600 Hz处最大,且在其他频率范围的传递率数值也较大;减振道床的道床至隧道壁横向振动传递率在700 Hz左右最大,其振动传递过程主要集中于300 Hz~700 Hz范围内。
3.2.3 振动传递规律分析
通过研究分析可见,不同道床的传递频率在不同位置和不同方向上有所不同,此现象的原因在于普通整体道床与减振道床两者轨道结构以及约束方式不同。
与普通整体道床相比,减振道床主要通过低刚度的减振垫层结构吸收列车引起的轨道振动能量,进而达到一定的减振效果。同时,由于减振垫层的存在,减振道床的整体约束更少,其钢轨与道床整体的振动响应相比普通整体道床更大,而钢轨与道床之间采用扣件连接,其刚度显著大于减振垫层。因此,在三者整体的约束差异情况下,减振道床钢轨至道床的振动传递相较普通整体道床大,而道床至隧道壁的振动传递相较普通整体道床小。
由于减振垫层的减振作用主要体现于对列车垂向振动能量的吸收,同时减振的频域更集中于对高频振动的隔振。因此在减振效果上,减振道床垂向振动的传递系数更小。对于不同道床而言,其振动传递在不同频率和方向上有所不同。
4 结语
(1)普通整体道床的下部与基础为刚性连接,道床板整体的约束较多,因此当道床板质量以及受到列车激励作用相同时,普通整体道床钢轨以及道床的振动响应将会略小于减振道床。
(2)减振道床的减振垫层将列车的振动能量通过自身的隔振作用进行了消耗,因此传递至隧道壁时,减振道床地段的隧道壁的振动响应普遍低于普通整体道床。但是由于减振道床主要耗散列车竖向的振动能量,因此对于水平方向的隔振效果有限。
(3)由于减振垫层的存在,减振道床的整体约束更少,其钢轨与道床整体的振动响应相比普通整体道床更大,而钢轨与道床之间采用扣件连接,其刚度差显著大于减振垫层与基础之间的刚度差。
(4)在钢轨、道床、隧道壁(基础)整体的约束差异情况下,减振道床钢轨至道床的振动传递率相较普通整体道床大,而道床至隧道壁的振动传递率相较普通整体道床小。
(5)由于减振垫层的减振作用主要体现于对列车垂向振动能量的吸收,同时减振的频域更集中于对高频振动的隔振。因此在减振效果上,减振道床垂向振动的传递系数更小,对于不同道床而言,其振动传递在不同频率和方向上有所不同。
(6)1/3 倍频程分析侧重于不同频率下同一测点位置的振动响应对比分析,传递函数分析更适用于不同频率下不同测点位置的振动传递对比分析,两种方法互为补充,对于评价地铁轨道的振动特性均具有十分重要的意义。
