局域共振型平板结构的低频振动与声辐射特性分析
2022-03-09周奇郑朱拥勇骆子寅
郭 彭,周奇郑,朱拥勇,骆子寅
(海军工程大学 兵器工程学院,武汉 430033)
水下航行器在航行过程中不可避免地会产生振动与噪声,强烈的振动与噪声会影响航行器的声隐身性能,进而降低其生存能力,结构辐射噪声是航行器噪声研究领域的重要分支,而其中低频噪声具有传播距离远,穿透力强等特点,因而成为航行器被探测的主要声学特征。平板结构是航行器中最常用的基础构件之一,抑制平板结构的低频振动与低频辐射噪声对提升航行器声隐身性能具有重要意义。
近年来,局域共振机理[1]的提出为水下航行器低频减振降噪设计提供了新的思路。2005 年开始,声物理学界有关局域共振结构的前沿成果逐渐引起了国内外减振降噪工作者的广泛重视。王刚等[2–3]率先通过理论和实验研究证实了局域共振机理应用于工程结构低频减振降噪的可行性,分别建立了无限周期结构下的局域共振杆结构、局域共振梁结构以及局域共振板结构,相关研究结果均表示通过在基体表面周期性附加局域共振单元形成的局域共振结构具有带隙特性,能够有效抑制结构的低频振动。Oudich 等[4–5]通过有限元和实验的方法分别对局域共振型平板结构的带隙特性进行了进一步研究,并指出局域共振机理在低频减振降噪方面的应用前景,有限元计算结果和实验结果均表明该结构中存在着低频带隙。Ma等[6]通过在平板表面附加圆柱型共振单元形成了局域共振型平板结构,并分析了其带隙形成机理,提出了该结构实现宽带完全带隙的设计方案。Xiao等[7]将均质薄板作为基体并在其表面周期附加“弹簧-质量”振子局域共振单元构成局域共振平板结构,利用平面波展开法计算了无限周期结构下的局域共振平板的低频带隙,并得到了带隙调控规律及其形成机理。吴健等[8]利用多频“双悬臂梁式”结构代替单一类型的谐振子单元,研究了多频局域共振型平板结构的低频带隙特性及其减振性能,研究发现多频局域共振平板结构可以产生多个低频带隙,通过改变双悬臂梁式的结构参数可以对带隙进行调控。文献[9]针对考虑声振耦合下的局域共振型平板结构的声振特性进行了分析,并研究了吸振器结构参数与位置参数对该结构低频振动与声辐射特性的调控规律,研究表明通过对吸振器各参数的适当调节,可有效控制平板结构的低频振动与低频辐射噪声。
综上所述,分析局域共振平板结构的声振特性对于水下航行器的低频减振降噪设计具有重要意义,而国内外对局域共振型平板结构声振特性的研究主要是针对无限大结构,而水下航行器中的实际工程平板结构均是有限大边界。为此,本文通过改变边界条件重新构建出四边简支边界条件下局域共振型平板结构的理论计算模型,并推导出耦合振动方程进而分析平板的低频振动与声辐射特性,然后分析元胞中吸振器固有频率比、阻尼比、元胞种类对平板声振特性的影响规律,最后利用粒子群算法[10]对其进行优化设计,研究结果有望为水下航行器的低频减振降噪设计提供理论指导。
1 声振特性理论计算模型
1.1 理论模型建立
为研究局域共振型平板结构的低频声振特性,建立如图1所示的理论计算模型。平板结构为四边简支板,假设平板周围为空气介质。在该平板上沿x和y 方向周期布置Qx和Qy个局域共振元胞,每个局域共振元胞中包含若干动力吸振器,且在平板x和y方向上的吸振器总数可分别记为M和N。该平板结构在坐标(x0,y0)处受到简谐激振力F(t)=F0sinωt的作用下发生振动,分析其低频声振特性。
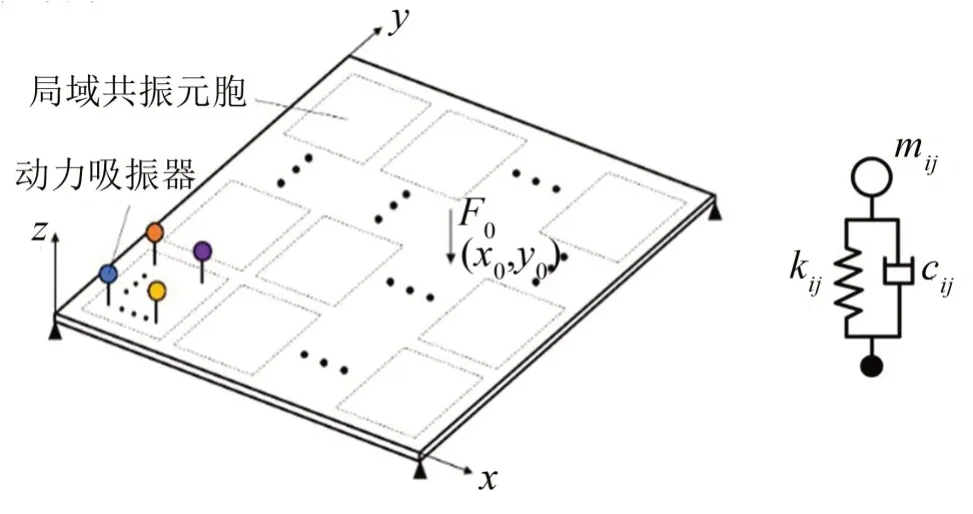
图1 局域共振平板结构声振模型
图1中平板上局域共振元胞之间的距离沿着x和y方向分别记为aj和bj,元胞中动力吸振器之间的距离沿着x和y方向分别记为ar和br,每个吸振器的坐标可表示为(xij,yij)。
1.2 声振特性计算方法
基于薄板Kirchhoff 假设,平板表面(x,y)处在t时刻的横向振动位移可以用w(x,y,t)表示,简记为w,记平板的长度为Lx、宽度为Ly、厚度为h、弹性模量为E、密度为ρ,泊松比为υ,力激励下的局域共振型平板结构的耦合振动方程可以表述为:
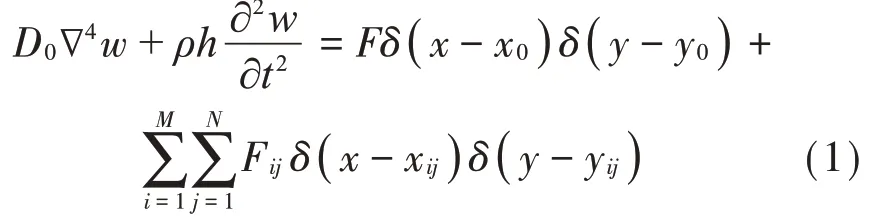
根据模态叠加法,平板的横向振动位移可以表示为:
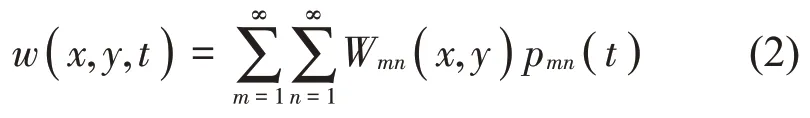
其中:Wmn(x,y)和pmn(t)分别为平板在四边简支边界条件下的固有振型函数和相应的模态位移。
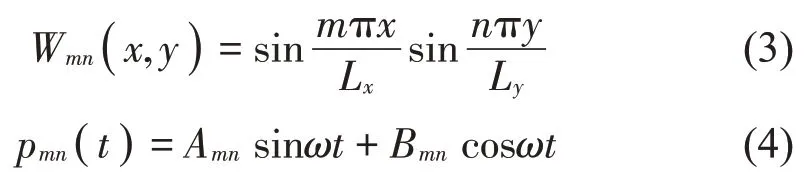
式中:Amn和Bmn分别为平板模态位移的正弦分量和余弦分量,w为激振角频率。
以单个动力吸振器作为研究对象,对其进行受力分析可知吸振器对平板的反作用力同时由弹簧的反作用力Fk和阻尼的反作用力Fc组成,因此可以表示为:

式中:

其中:w(xij,yij,t)表示坐标(xij,yij)处平板在t时刻的横向振动位移,kij、cij和uij分别表示坐标(xij,yij)处振子的弹簧刚度、阻尼和横向振动位移。
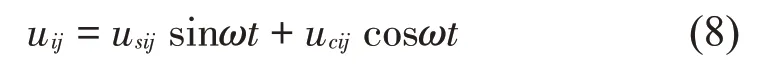
其中:usij和ucij分别表示坐标()xij,yij处吸振器横向振动位移的正弦分量和余弦分量。
分析各吸振器与平板的耦合振动,可得到局部振动耦合方程:

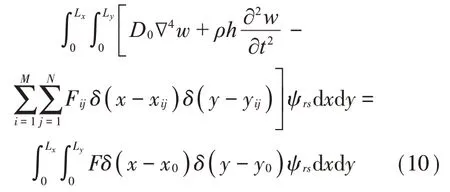
其中:
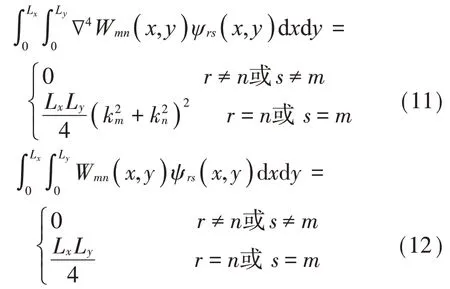
将式(2)、式(5)、式(11)、式(12)代入方程式(10),整理化简后与方程(9)联立,取平板结构的前Q∙Q阶模态参与计算,将方程组写成矩阵形式:
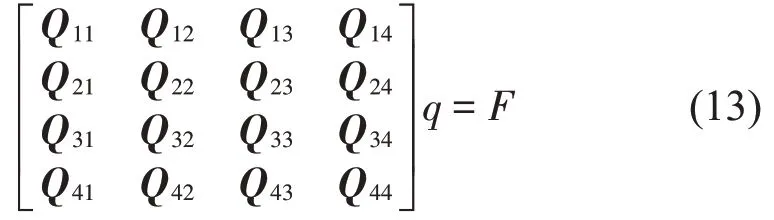
其中向量q为矩阵方程的待求未知向量:

为能够准确的对矩阵方程式(13)中的各元素进行描述,定义如下表达式:
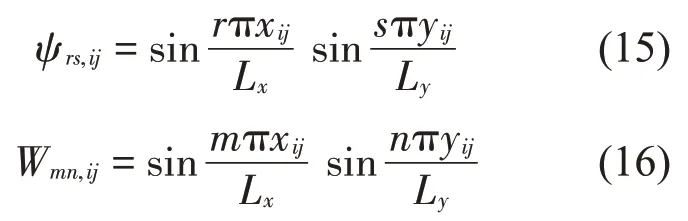
式中:ψrs,ij和Wmn,ij分别代表平板r′s阶模态以及m′n阶模态坐标(xij,yij)处的振型函数。
矩阵Q11可以表示为一个对角矩阵和另一个普通矩阵之和的形式:

其中:
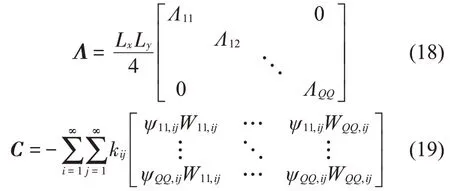
对角矩阵Λ为QQ∙QQ阶矩阵,对角线上元素可以表示为,该矩阵代表的是平板结构的固有振动特性;矩阵C同样为QQ∙QQ阶矩阵,该矩阵代表的是吸振器的刚度成分对平板振动特性的影响。
矩阵Q12中的元素及含义与矩阵C类似,可以表示为:
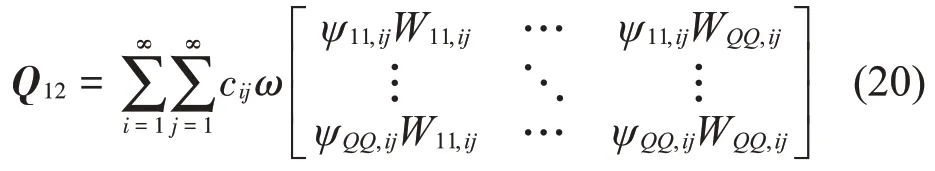
矩阵Q12为QQ∙QQ阶矩阵,该矩阵代表的是吸振器中的阻尼成分对平板振动特性的影响。
矩阵Q13可以表示为:

矩阵Q13为QQ∙MN阶矩阵,该矩阵代表的是吸振器的刚度成分对吸振器固有振动特性的影响。
矩阵Q14可以表示为:

矩阵Q14为QQ∙MN阶矩阵,该矩阵代表的是吸振器的阻尼成分对吸振器固有振动特性的影响。
矩阵Q33为对角矩阵,可以表示为:
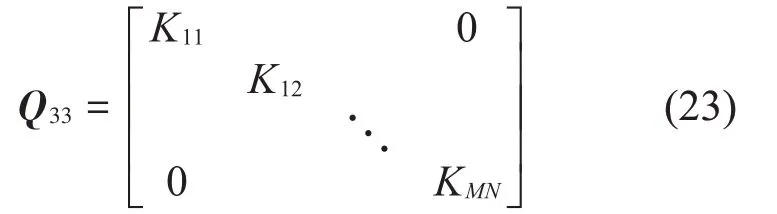
对角矩阵Q33为MN∙MN阶矩阵,对角线上元素可以表示为KMN=mMNω2-kMN,代表的是单个吸振器的刚度成分对吸振器振动特性的影响。
矩阵Q34为与Q33类似,为对角矩阵,可以表示为:
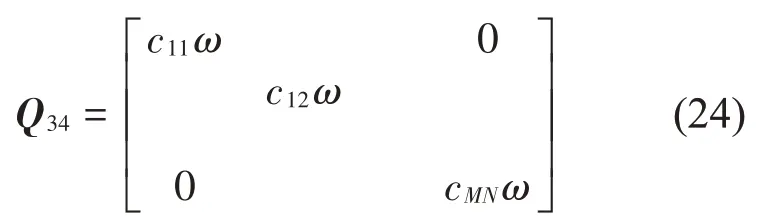
对角矩阵Q34为MN∙MN阶矩阵,该矩阵代表的是单个吸振器的阻尼成分对吸振器振动特性的影响。
矩阵方程式(13)等号左侧系数矩阵中其他未知矩阵与上述已知矩阵有如下对应关系:Q21=-Q12,Q22=Q11,Q23=-Q14,Q24=Q13,Q31=QT13,Q32=QT14,Q41=-QT14,Q42=QT13,Q43=-Q34,Q44=Q33。
矩阵方程式(13)右侧力向量代表的是作用在平板表面坐标()x0,y0处简谐激振力对平板振动特性的影响,可以表示为:

该向量为2(QQ+MN)∙1 维列向量,向量中的元素为
将式(14)至式(25)代入矩阵方程式(13),通过对矩阵方程的求解,便可以得到局域共振型平板结构表面平均振速与激振频率的关系函数V(ω),进而计算出局域共振型平板结构表面平均振速级:

式中:V0为计算参考振速,取值为V0=5×10-8m/s。
得到局域共振型平板结构耦合方程之后就可以利用平板的表面声压求得平板的辐射声功率,即采用对结构辐射表面声压与其表面振速的乘积在整个辐射表面内进行积分的方式进行求解。
根据Rayleigh 积分公式,平板辐射表面在平板上方介质中(x′,y′,z′)处的声压可以由如下积分形式表示:
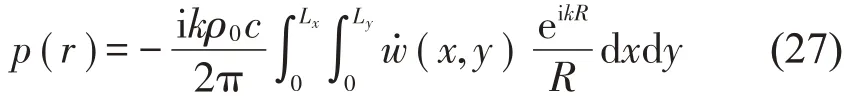
则可以得到平板结构的辐射声功率积分表达式:
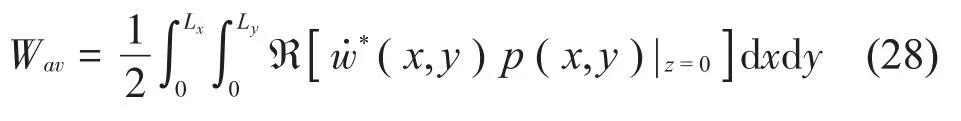
其中*和ℜ分别表示复数的共轭和实部
结合式(2)可以得到平板结构辐射声功率的余弦和正弦分量如下:
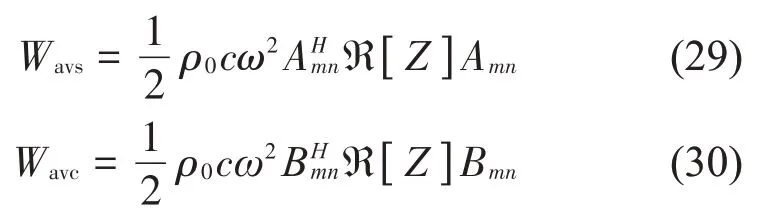
式中:Zmn=ζmn+iχmn为声辐射阻抗,各元素可以表示为:
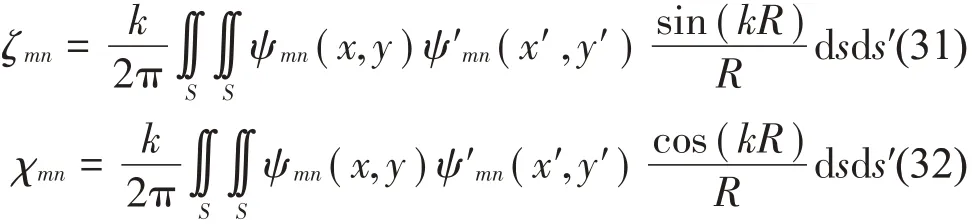
其中:ζmn和χmn分别表示结构的自辐射阻和自辐射抗。
进一步分析可得到平板结构的表面辐射声功率计算表达式为:

则有声辐射功率级:

其中取参考声功率W0=1×10-12W。
2 理论模型求解及分析
本节针对局域共振型平板结构的声振模型展开研究,并给出一个理论计算的简单算例,分别通过解析法和有限元软件COMSOL进行对比理论计算。
考虑算例中局域共振型平板结构为空气介质中四边简支平板,在平板中点位置施加激振力,激振力的幅值为1 N,激振频率范围为5 Hz~300 Hz,结构的几何及材料参数如表1所示。其中E、ρ、υ 分别表示平板的弹性模量、密度、泊松比,Lx、Ly、h分别表示平板的长度、宽度、厚度,计算出该简支平板结构的前5×5阶固有频率如表2所示。

表1 平板的参数
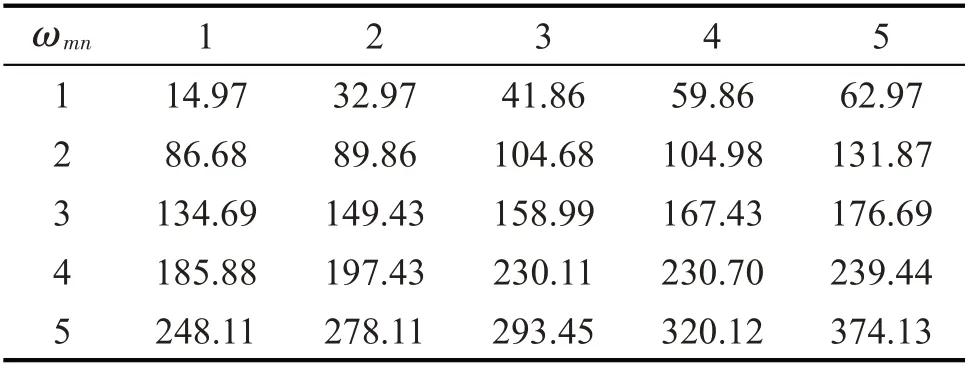
表2 平板的前5阶固有频率/Hz
在该平板结构表面均匀布置8×10 的吸振器阵列,假定每个吸振器的参数均相同,取吸振器的初始计算参数:质量m=0.022 5 kg、固有频率比λ=4.2、阻尼比ζ=0.02。分别通过解析法与有限元法计算得到平板结构表面平均振速级曲线,并对比如图2所示。

图2 解析解与有限元解对比
由图2可知,在目标频段解析法和有限元法得到的振速曲线均出现了若干共振峰和减振频带,且频带的频率位置对应着吸振器的固有频率(62.87 Hz)。为有效说明解析结果和有限元结果的一致性,现定义两者之间的平均误差度为各个计算频率位置处误差度的数学平均值,误差度可表述为两者数据的差值占解析解数据的百分比,计算可得在5 Hz~300 Hz 范围内解析解与有限元解之间的平均误差度仅为0.58%,具有较高的吻合度,同时各个共振峰对应的频率也基本相同,进一步说明了解析计算方法的有效性。
3 低频声振特性研究
本节针对局域共振型平板结构附加吸振器的固有频率比、阻尼比及元胞种类对平板声振特性的影响规律展开研究,假定该平板结构的边界条件为四边简支,在其表面均匀布置8×10 的吸振器阵列,吸振器的总质量为平板质量的1/5,考虑平板的几何和材料参数与第2节算例相同。
将平板上附加吸振器阵列划分为单振子元胞,分析元胞中吸振器固有频率比λ对平板声振特性的影响规律,取各吸振器的阻尼比ζ=0.02,此时吸振器固有频率比指的是吸振器的固有频率和平板(1,1)阶固有频率的比值,分别取值λ=1、λ=5.8、λ=7.4、λ=15.4,对应的频率分别为14.97 Hz、86.83 Hz、110.78 Hz、230.54 Hz。分别计算出吸振器不同固有频率比下5 Hz~300 Hz范围内局域共振型平板结构表面平均振速级和辐射声功率级曲线,如图3和图4所示。

图3 振子固有频率比对平板振动特性的影响

图4 振子固有频率比对平板声辐射特性的影响
由图3和图4可以看出平板表面附加单振子元胞后,在目标频段存在明显的减振频带,且每个频带的频率位置均对应吸振器的固有频率,随吸振器固有频率比的增大,频带向高频移动且始终保持在吸振器固有频率附近。在频带左侧和右侧的共振峰分别呈现出向高频和低频移动的规律,且峰值均有所降低,说明在平板表面布置局域共振元胞不仅仅能够产生减振频带,还会对其他频率位置处平板结构共振峰的大小以及频率位置产生影响。针对水下航行器的低频减振降噪设计,可以根据振动与噪声的频率范围来选择具有相应固有频率的动力吸振器。
将平板上附加吸振器阵列划分为单振子元胞,分析元胞中吸振器阻尼比ζ对平板声振特性的影响规律,假定各吸振器的固有频率比均为λ=5.8,吸振器阻尼比分别取值ζ=0.02、0.1、0.2。分别计算出吸振器不同阻尼比下5 Hz~300 Hz范围内局域共振型平板结构表面平均振速级和辐射声功率级曲线如图5和图6所示。

图5 振子阻尼比对平板振动特性的影响
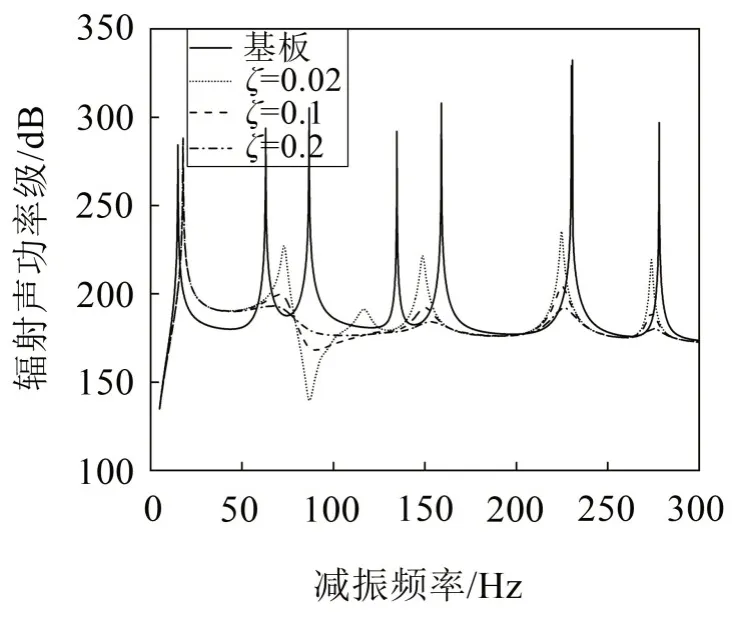
图6 振子阻尼比对平板声辐射特性的影响
由图5和图6可知,平板表面布置若干单振子元胞后,在目标频段出现了明显的减振频带且对应着吸振器的固有频率(86.83 Hz),随着吸振器的阻尼比由0.02逐渐提高至0.2,吸振器对平板的反共振作用减弱,频带位置处的减振性能下降,频带被拓宽,而在整个目标频段曲线逐渐变得光滑,各共振峰幅值变小。因此,吸振器阻尼的大小不会改变频带以及各共振峰的位置,只会对频带处减振降噪性能以及频带宽度产生影响,并且吸振器阻尼的增大会使得整个目标频段平板结构的振动均有所降低。针对水下航行器的低频减振降噪设计,可在吸振器中适当引入阻尼成分,保证减振降噪性能的同时,有效拓展频带宽度。
前文中分析了平板上附加吸振器的固有频率比、阻尼比对平板声振特性的影响规律,均针对单振子元胞。为进一步研究元胞种类对平板声振特性的影响规律,将平板上附加的吸振器阵列分别划分为单振子、双振子、四振子元胞,首先假定各吸振器的阻尼比均为z=0.02,并取单振子元胞中吸振器固有频率比l=4.2,对应的频率为62.87 Hz;双振子元胞中吸振器固有频率比为:l1=4.2、l2=5.8,对应的频率为:62.87 Hz、86.83 Hz;四振子元胞中吸振器固有频率比为:l1=4.2、l2=5.8、l3=7.4、l4=9.2,对应的频率为:62.87 Hz、86.83 Hz、110.78 Hz、137.68 Hz。分别计算出不同元胞种类下5 Hz~300 Hz范围内局域共振型平板结构表面平均振速级和辐射声功率级曲线如图7和图8所示。
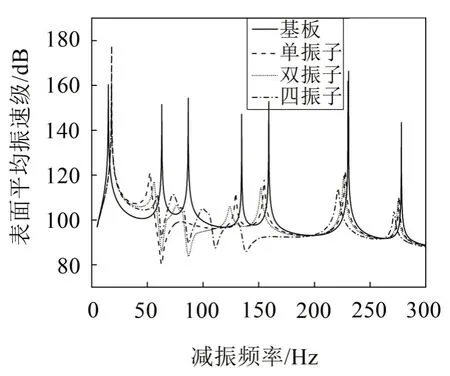
图7 元胞种类对平板振动特性的影响
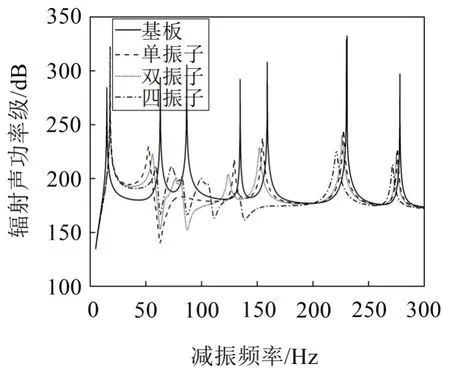
图8 元胞种类对平板声辐射特性的影响
由图7和图8可知,在目标频段单振子、双振子、四振子元胞下的平板结构声振曲线分别出现了1个、2个、4个减振频带,且每个频带的频率位置分别对应着元胞中各吸振器的固有频率,在吸振器总数一定的情况下,同一个频带处单振子元胞的低频减振降噪性能要高于多振子元胞。另外,由图中可以看出减振频带的频率位置只由元胞中吸振器的固有频率决定,频带的数量只与元胞中吸振器的种类相关,与激振频率的大小及共振峰的位置无关。水下航行器所产生的振动与噪声可能包含着多个频率范围,多振子元胞的设计方式可针对不同频率下的振动与噪声进行有效控制。
4 声振特性优化
前文分析得到了5 Hz~300 Hz范围内吸振器固有频率比、阻尼比以及元胞种类对平板声振特性的影响规律,本节将利用粒子群算法分别对单振子、双振子、四振子元胞下的局域共振型平板结构进行优化设计。
假设空气介质中的四边简支平板受到中点位置施加的激振力发生振动,激振力的幅值大小为1 N,激励频率范围为5 Hz~300 Hz,空气密度为ρ0=1.293kg/m3,声速为c0=344 m/s。假定平板的几何及材料参数与第2 节算例一致,在其表面均匀布置8´10 的吸振器阵列,并将吸振器阵列分别划分为单振子、双振子、四振子元胞,在保证吸振器总数不变的情况下,平板表面附加的吸振器总质量为平板质量的1/5,以此为约束条件取优化变量分别为元胞中吸振器的固有频率比l和阻尼比z,取目标函数为5 Hz~300 Hz范围内平板表面平均振速级Lv(ω)和辐射声功率级Lp(ω)的关系表达式J,表示如下:
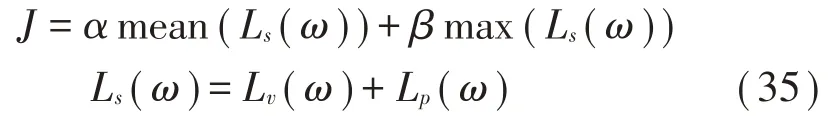
其中:S为目标频段参与计算的频率总数,a和b分别为分配给平板表面平均振速级和辐射声功率级的平均值和最大值的权重系数,这里可以取a=0.4、b=0.6,并确定优化变量的取值范围为:

经粒子群算法优化后,各元胞中吸振器的固有频率比l和阻尼比ζ优化参数结果如表3所示。

表3 动力吸振器参数优化结果
将优化后各元胞中吸振器的参数代入耦合振动方程,计算出目标频段平板表面平均振速级和辐射声功率级曲线如图9和图10所示。
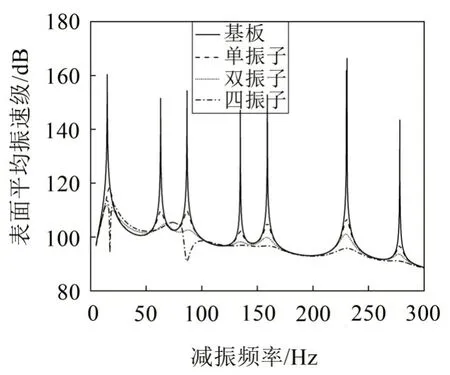
图9 优化前后空气中平板表面平均振速级
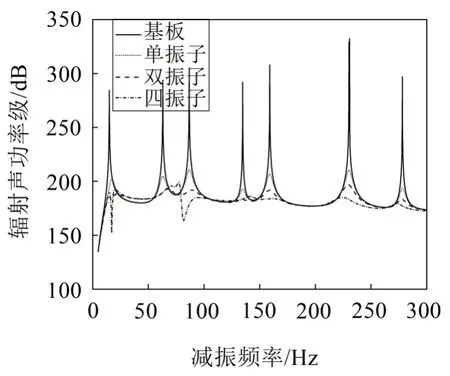
图10 优化前后空气中平板辐射声功率级
由图9和图10 可知,优化后的局域共振型平板结构表面平均振速级和辐射声功率级都有所改善,尤其是对各共振峰的控制尤为明显。基板、单振子、双振子、四振子元胞下的目标函数数值分别为414.49 dB、305.49 dB、291.08 dB、293.71 dB,进而可得到单振子、双振子、四振子元胞在目标频段的减振效率分别为26.3%、29.8%、29.1%,优化后的双振子元胞的减振效率要高于单振子、四振子元胞,但是四振子元胞存在更明显的减振频带,对某些频率下低频振动与噪声具有更好的控制效果。为了简化该局域共振型平板结构的设计,采用双振子元胞设计即可。
5 结语
本文尝试将局域共振机理应用于水下航行器的低频减振降噪设计,以四边简支平板结构为研究对象,提出在其表面均匀布置局域共振元胞的低频减振降噪方法,构建了动力学模型并推导出其耦合振动方程,采用模态叠加法和谐波平衡法导出了耦合振动方程的解析解;分析了元胞中吸振器固有频率比、阻尼比、元胞种类对平板声振特性的影响规律;采用粒子群算法对5 Hz~300 Hz范围内局域共振型平板结构进行了优化设计,得到以下主要结论:
(1)局域共振型平板结构在目标频段能够产生抑制其低频振动与噪声的频带,且频带的频率位置与元胞中吸振器的固有频率对应。
(2)随着吸振器阻尼的增大削弱了吸振器对平板的反振动作用,拓宽了减振频带的同时使频带处减振降噪性能减弱。
(3)多振子元胞较单振子元胞具有多个减振频带,频带的叠加作用使得多振子元胞具有更优越的低频减振降噪性能。
(4)经粒子群算法优化后,在目标频段单振子、双振子、四振子元胞的减振降噪效率分别可达到26.3%、29.8%、29.1%。
通过改变元胞中吸振器的各结构参数可调控局域共振型简支平板结构的低频减振降噪性能,研究结果可为水下航行器的低频减振降噪设计提供参考。
