计及弹性响应的需求侧资源与软开关联合规划

葛少云，李俊锴，刘 洪，王立永，王鹏翔，王成山

计及弹性响应的需求侧资源与软开关联合规划

葛少云1，李俊锴1，刘 洪1，王立永2，王鹏翔3，王成山1

(1. 天津大学智能电网教育部重点实验室，天津 300072；2. 国家电网北京市电力公司，北京 100031；3. 中国电建集团河南省电力勘测设计院有限公司，郑州 450007)

针对软开关(soft open point，SOP)规划研究中尚未涉及需求侧资源响应特性及其位置选择的问题，提出了一种考虑可平移与可削减负荷资源响应不确定性的联合规划模型和规划运行整体求解方法．首先，基于不同类型负荷的主要构成及需求响应特性分析，构建了需求侧资源可平移与可削减两类响应特性的三角隶属度模糊模型；其次，以配电公司年综合费用最小为目标，建立了需求侧资源和智能软开关模糊机会约束规划模型，实现了对需求侧资源投入成本、软开关建设运行费用、网络损耗费用以及弃风弃光成本的综合分析；再次，基于模糊变量的清晰等价类变换、等效替代以及多面体线性化技术，提出了模糊机会约束二阶锥规划模型转化为混合整数线性规划模型的数学方法，实现了规划层与运行层利用CPLEX求解器在Matlab平台的整体求解．最后，结合某地区配电系统实际算例分析了内嵌运行策略的需求侧资源与软开关联合规划结果．算例结果表明：需求侧资源与软开关的联合规划实现了不同规划对象的优势互补，既保证了规划方案的经济性，降低了配电系统的网络损耗，同时也提高了对分布式电源的消纳能力．

软开关；需求侧资源；模糊机会约束规划；多面体线性化

近年来，以智能软开关为代表的柔性互联[1]技术发展迅速，在降低馈线损耗、稳定节点电压和恢复系统故障等领域得到广泛应用并逐渐成为配电网侧的关键元素．与此同时，随着智能用电水平的进步和电力市场制度的完善，用户负荷性质逐渐发生转变，大量灵活可控的需求侧资源受到广泛关注并成为负荷侧研究的焦点．为提升可再生能源的消纳能力[2]，实现“碳峰值”和“碳中和”的国家战略目标，研究本地电网侧和负荷侧资源一体化协同规划方法具有重要意义．

目前，国内外学者对软开关的规划问题已有大量研究成果，主要体现出由单一规划向协同规划扩展的特点．单一规划是软开关前期研究的重点，在构建软开关数学模型的基础上，围绕配电网关注的投资成本、网络损耗及电压质量等指标实现软开关的优化配置．文献[3]提出了规划与运行双层交替的软开关优化配置方法，分析了软开关接入后对网络损耗和节点电压影响．文献[4]提出了考虑正常运行与发生故障两种场景的SOP选址定容方法，兼顾了配电网运行的经济性与可靠性．协同规划方法是近年来软开关研究的热点，对实现不同规划对象之间的优势互补和资源重组意义重大．文献[5-6]在软开关规划的基础上联合了在潮流调控中发挥无功支撑作用的电容器组，提升了软开关配置和配电网运行的经济性．文献[7]提出了一种有源配电网分布式电源与软开关协调规划模型，满足了配电网规划中分布式电源运营商与配电公司之间不同的利益需求．文献[8]提出了含软开关配电网中分布式储能的规划方法，充分挖掘了储能系统的经济价值．但在当前软开关协同规划研究中，主动配电网中大量灵活可控的需求侧资源[9-10]没有得到充分重视．文献[11]提出了考虑需求响应与软开关的配电网重构模型，降低了配电网重构费用并提高了新能源消纳能力．该模型揭示了需求侧资源与软开关对配电网优化运行的协同作用机理，但缺乏对需求侧资源与软开关联合最优配置的深入分析，也忽略了需求侧资源在响应中的不确定性．

另一方面，软开关规划问题通常采用启发式算法确定其位置容量组合，文献[12]将SOP安装位置与容量的组合看作粒子所处的状态，将该组合下的目标函数值即年综合费用看作粒子所处状态的能量，利用模拟退火算法解决了SOP选址定容问题．文献[13]利用粒子群优化算法求解规划层模型并引入自适应权重和收缩因子对算法进行改进，最大限度地保证得到最优的SOP选址定容方案．文献[14]提出了基于动态GA编码的SOP选址策略，将SOP的接入位置由同一电压等级的联络开关处扩展至不同电压等级的配电网之间．但是对于规模较大的配电系统而言，随着软开关待选的位置容量组合增加，启发式算法的求解速度和寻优效率均会明显下降，求解结果的全局最优性也更加难以保证．

针对以上不足之处，本文首先分析工业负荷、商业负荷、居民负荷的主要构成，结合用户响应意愿的不确定性构建需求侧资源可平移与可削减两类响应特性的三角隶属度模糊模型；其次，以配电公司需求侧资源投入成本、软开关建设运行费用、网络损耗费用以及弃风弃光成本总和最小为目标，建立考虑不确定性的需求侧资源和智能软开关联合规划模型；再次，对目标函数和约束条件中的模糊变量进行清晰等价处理，将不确定性变量转化为与置信水平相关的确定性变量，同时对软开关的容量约束进行多面体线性化处理，将二阶锥规划模型转化为混合整数线性规划模型并在Matlab平台上利用CPLEX求解器实现求解．最后结合某地区配电系统实际算例，验证本文所提方法的有效性．

1 考虑弹性响应的需求侧资源建模

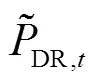
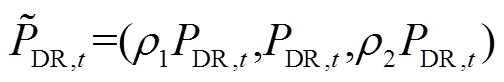
需要注意的是，不同类型负荷DR响应存在较大区别，工业负荷主要是具有固定流程的流水线作业负荷，其响应模式以负荷平移为主；商业负荷主要是温控负荷和照明负荷，其响应模式以负荷削减为主；居民负荷主要是家用电器，其响应模式以负荷削减为主．基于上述分析，分别构建需求侧资源中可平移负荷和可削减负荷的响应模型．

图1 三角隶属度模糊变量

1) 可平移负荷

2) 可削减负荷

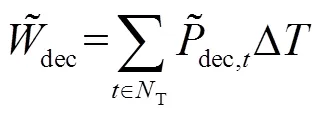
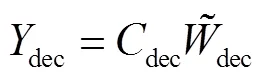
2 需求侧资源与软开关联合规划模型

2.1 SOP功能分析和数学建模

SOP是一种安装于传统联络开关处的新型电力电子装置，能够平衡馈线负载、优化潮流分布和降低网络损耗，并提供无功电压支撑、改善馈线电压水平和提高分布式电源消纳能力．SOP的功能实现主要基于全控型电力电子器件，具体方式[17]主要包括统一潮流控制器(UPFC)、静止同步串联补偿器(SSSC)和背靠背电压源变流器(VSC)．

本文以背靠背电压源型变流器为例，选取-dc控制作为SOP的控制模式[18]，研究配电网中SOP规划问题．此时SOP的可控变量主要包括控制端口的交流有功功率、交流无功功率和dc控制端口的交流无功功率和直流电压．对于交流侧而言，其数学模型如下所示．

1) SOP有功约束

式中：SOPa和SOPb分别为节点和节点VSC注入的有功功率；Sloss为SOP的能量传输损耗；为VSC的损耗系数．

2) SOP无功约束

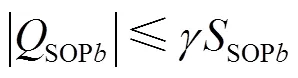
式中：SOPa和SOPb分别为两个VSC注入的无功功率；为SOP运行时功率因数角正弦的绝对值；SOPa和SOPb分别为接入节点和的VSC容量．

3) SOP容量约束

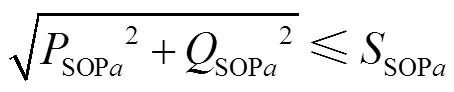
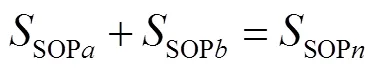
式中SOPn为第个SOP的安装容量．

2.2 目标函数

模型的目标函数是配电公司年综合费用最小，数学表达式为

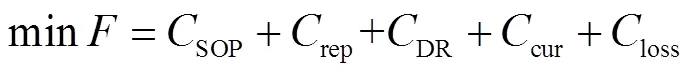
表达式中各部分变量的含义和计算方法如下．

1) SOP建设投资成本SOP

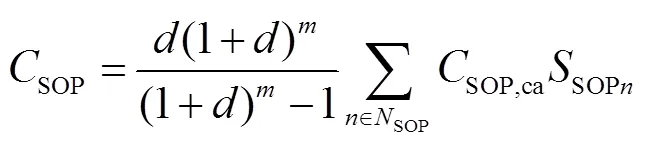
式中：为贴现率；为SOP运行年限；SOP,ca为SOP单位容量投资成本；SOP为SOP安装总数．

2) SOP运行维护成本rep

式中1为SOP运行维护系数．

3) 需求侧资源成本DR

式中：k为0～1变量，代表配电公司是否选择配电网节点用户的需求侧资源；为配电网节点总数；X和Y分别为第个负荷点的容量成本和电量成本，不同类型负荷的响应方式存在差异；ca为需求侧资源的单位容量成本；DRi为第个负荷点用户预留的响应容量．

4) 分布式电源弃风弃光成本cur

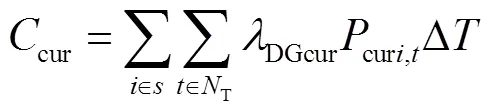
式中：DGcur为弃风弃光的单位成本；curi,t为时刻弃风弃光的功率．

5) 配电网损耗成本loss

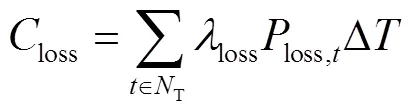
式中：I,t为时刻流过支路的电流；r为支路的电阻；a为支路的集合；loss,t为时刻配电网损耗功率；loss为配电网损耗的单位成本．

2.3 约束条件

1) 配电网潮流约束

为了综合考虑用户弹性响应和分布式电源出力的不确定性，本文采用模糊机会约束描述节点功率平衡[18]，进而得到配电网潮流约束如下．

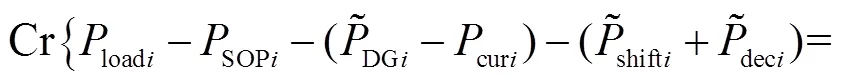
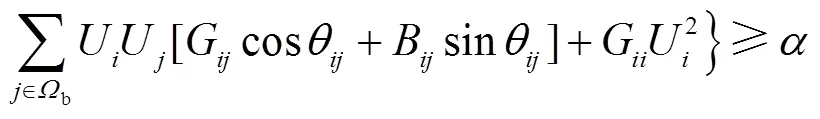
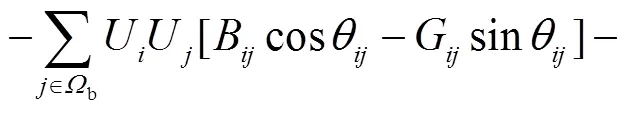
2) 需求侧资源约束

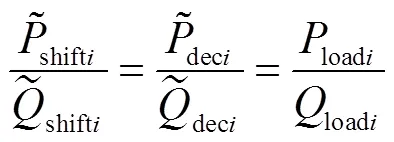
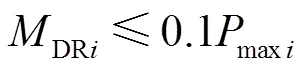
式中maxi为节点的负荷量

此外，该优化模型还需包括SOP相关约束，见式(6)～式(13)．

3 模型求解

可以看出，上述模型的目标函数和约束条件中均包含模糊变量，并且配电网潮流约束和SOP容量约束均为非线性约束[19]，直接求解较为困难．本文先将模糊变量处理成清晰等价类[20]，再将二阶锥约束通过多面体线性化技巧[21]进行转化，最后对于等价后包含规划与运行的混合整数线性规划模型，采用成熟的商业软件实现整体求解．

3.1 模糊变量的处理

根据不确定规划理论，对于约束条件式(22)和式(23)中的模糊变量，可以处理为清晰等价类，表达式分别为

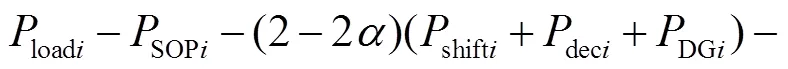
式中2为分布式电源预测出力的隶属度参数．

式(27)和式(28)经过处理后，将不包含不确定性变量，此时节点电压与支路电流约束为

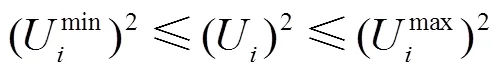
(30)

此外，对于目标函数中可削减负荷和可平移负荷的电量成本shift和dec可以处理为悲观值，表达式分别为

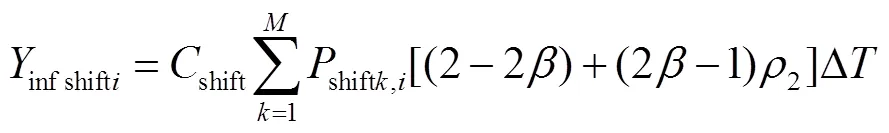
式中为悲观值的置信度．

3.2 非线性模型的转化

对于配电网潮流约束、节点电压与支路电流约束，利用D、E和F对式(27)～式(30)进行变量替换，即可转化为线性约束[12]．

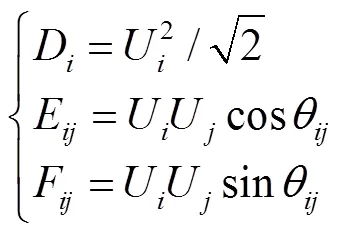
转化后的式(27)～式(30)分别为

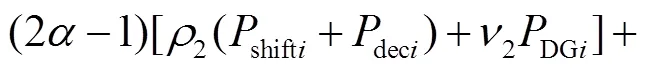
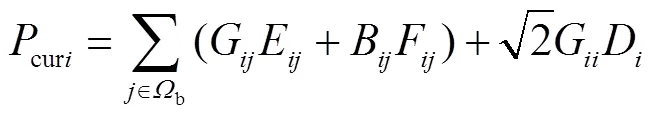
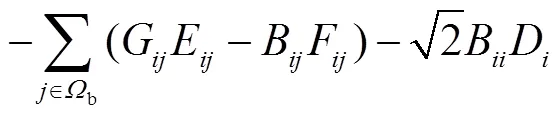
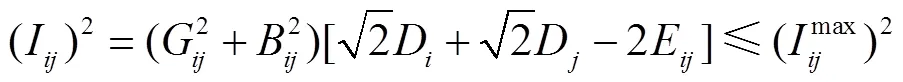
对于SOP运行约束中的式(10)和式(11)，其本身为二阶锥形式，可以直接采用商业软件进行求解．但为加快模型的求解速度，本文采用多面体线性化技巧对其进行转化，具体过程如下．

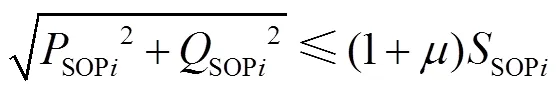
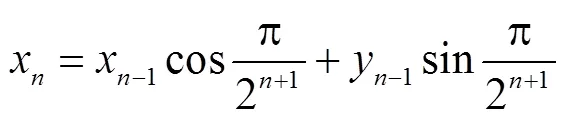
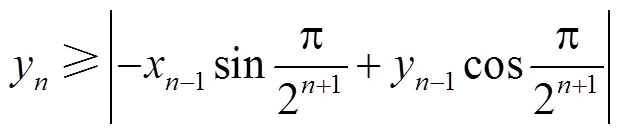
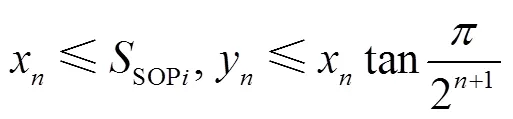
式中：x和y均为辅助变量；为松弛系数．

利用上述等式递推公式(40)可以消除个等式约束和个变量x，从而把关于变量(SOPi、SOPi、SOPi)的三维二阶锥约束近似等价于一组关于变量(SOPi，SOPi，SOPi，0)和＋1个变量(y，＝0，1，…，)的线性不等式约束．其中的计算方法为

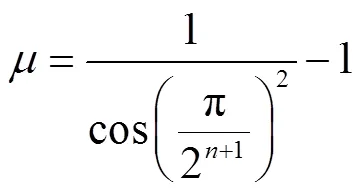
当选择＝8时，＝1.88×10-5，此时多面体线性化精度几乎达到100%[22]．

4 算例分析

4.1 算例概况

以某地区实际配电系统作为算例，系统网络结构和节点负荷类型如图2所示．SOP相关参数参见文献[12]．不同类型用户的典型负荷特性曲线参见文献[23]，分布式电源预测出力的三角隶属度特性参见文献[16]．需求侧资源配置的单位容量成本和不同类型负荷单位电量成本参见文献[24]．配电公司可选择作为需求侧资源的负荷节点上限为30个．一天内配电公司对两类负荷调度时长的上限均为3h．模型转化后的混合整数线性规划问题在Matlab中通过调用CPLEX求解器实现求解．

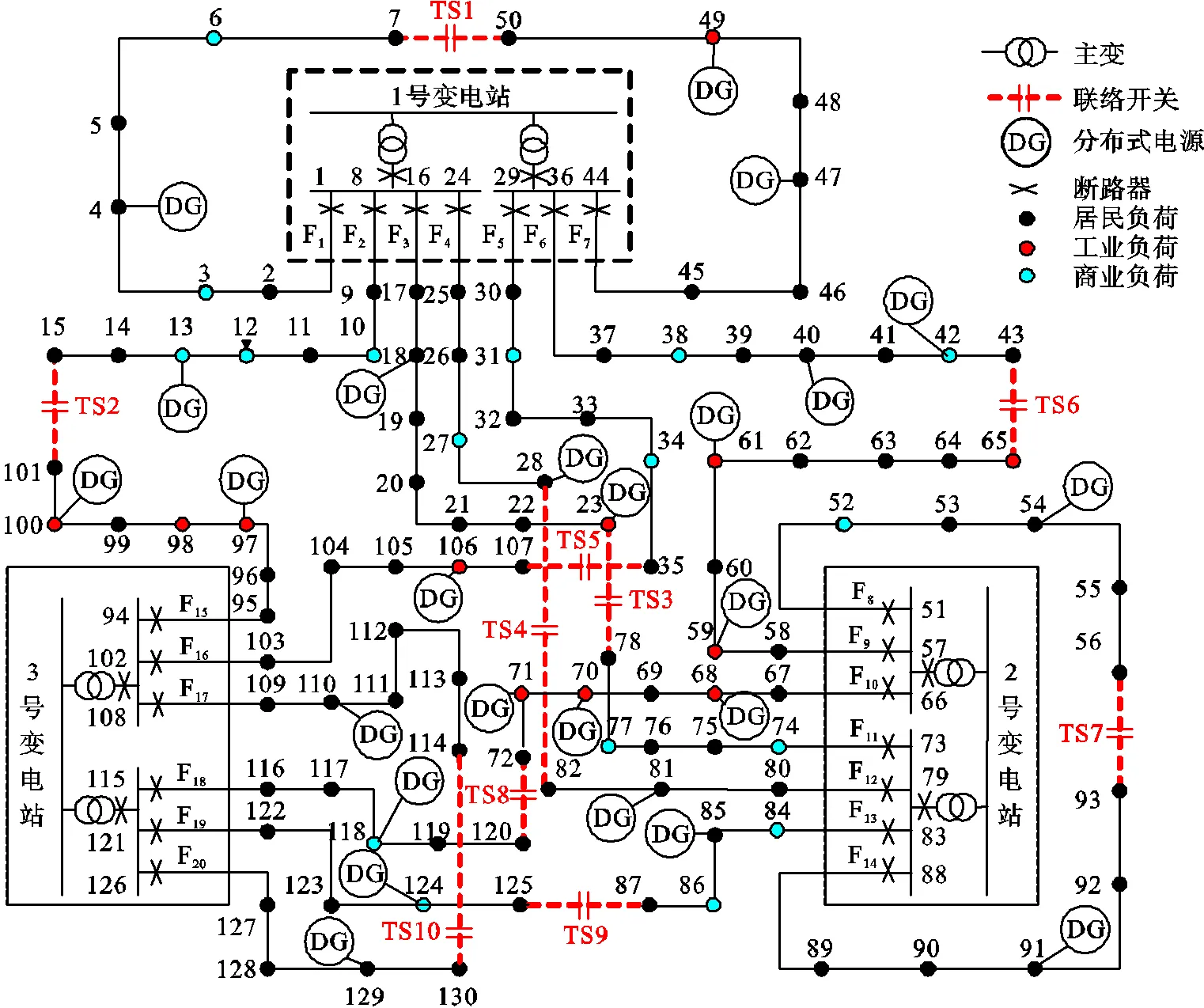
图2 配电系统网络结构

4.2 联合规划结果对比分析

为说明需求侧资源与软开关联合规划的效果，本文设置以下方案进行对比分析．

方案1 仅考虑需求侧资源．

方案2 仅考虑SOP．

方案3 综合考虑需求侧资源和SOP．

分布式电源渗透率为60%，模糊机会约束置信度和目标函数悲观值置信度均为0.9，得到SOP与需求侧资源规划结果分别如表1和表2所示，各方案综合成本如表3所示．

表1 SOP选址定容结果

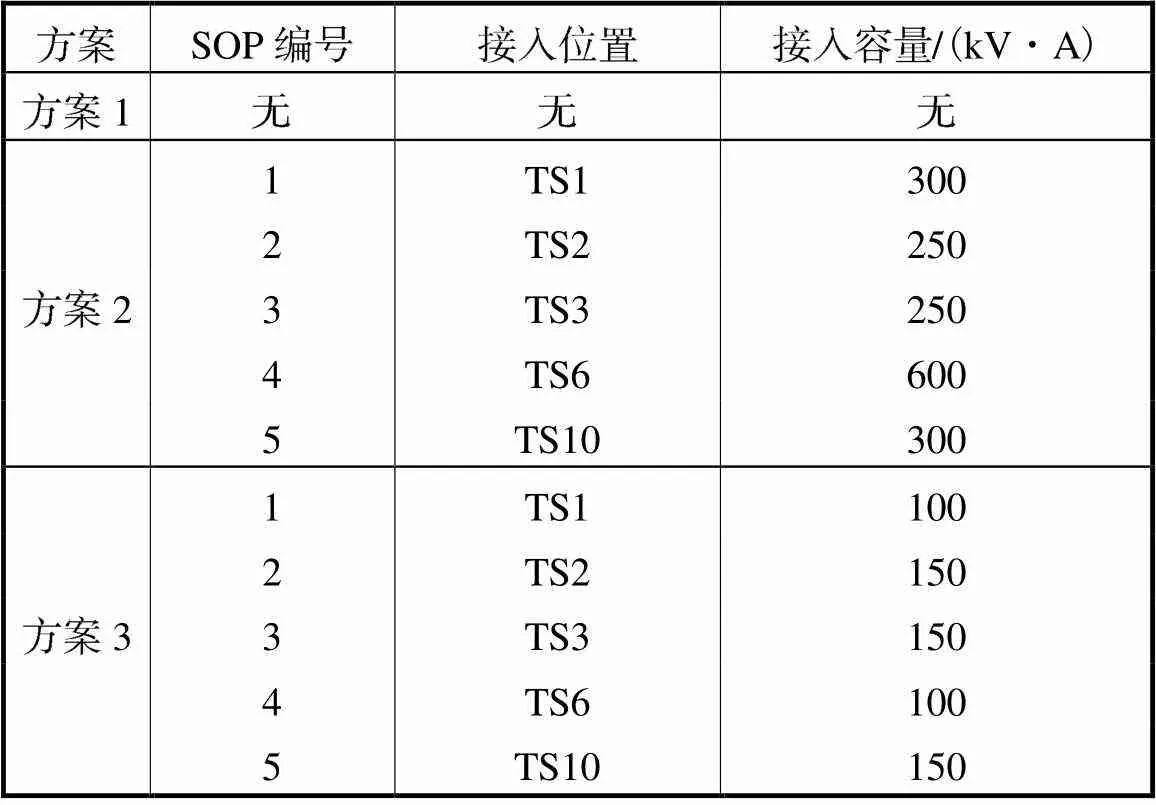
Tab.1 Siting and sizing results of SOP

表2 需求侧资源规划结果

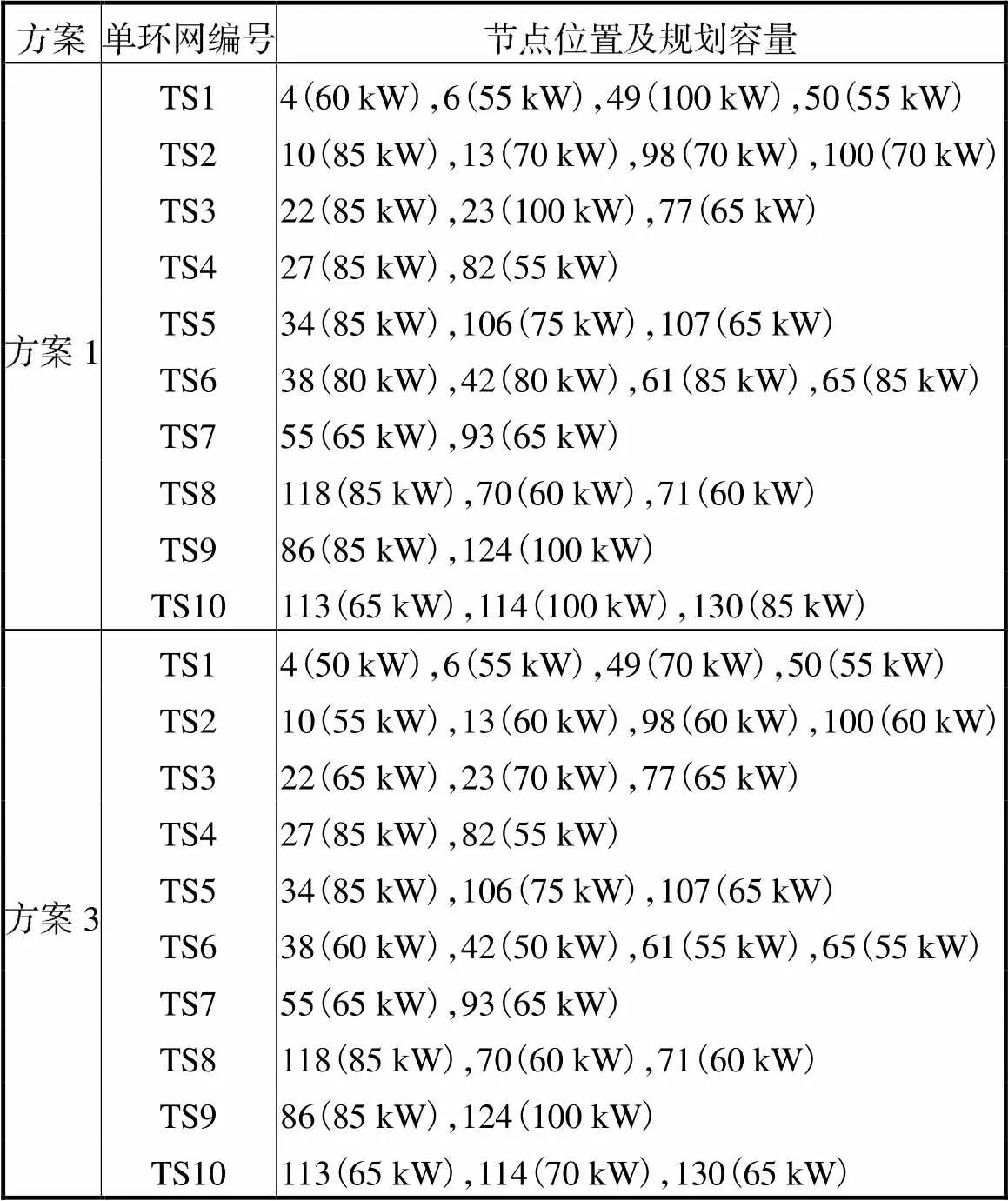
Tab.2 Planning results of demand-side resources

表3 各规划方案综合费用

Tab.3 Comprehensive cost of various planning schemes 　万元

分别对比方案1和规划前的结果以及方案2和规划前的结果，可以发现需求侧资源管理和智能软开关配置均起到了提高分布式电源渗透率、降低网络损耗的积极功效．其中方案1相比规划前总成本减少了12.12万元，弃风弃光成本减少了7.03万元，损耗成本减少了17.16万元；方案2相比规划前总成本减少了28.08万元，弃风弃光成本减少了9.62万元，损耗成本减少了36.26万元．方案2和方案1相对而言，单独规划SOP的效果更为明显．这是因为SOP可以从有功功率和无功功率两方面改善配电系统的运行现状，既能够实现有功调控、平衡馈线负载、降低网络损耗，又能够提供无功支撑、降低节点电压、提高新能源渗透率．

进一步对比方案3和方案1的结果以及方案3和方案2的结果，可以发现需求侧资源与SOP联合规划方案在实现分布式电源完全消纳的基础上，进一步降低了网络损耗和综合费用．这说明联合规划对实现不同规划对象之间的优势互补和资源重组具有重大意义．

4.3 分布式电源渗透率灵敏度分析

在方案3的基础上改变分布式电源渗透率，得到不同渗透率下需求侧资源与SOP联合规划成本的变化情况，如表4所示．

表4 不同分布式电源渗透率下的综合费用

Tab.4 Comprehensive cost in various penetrations of DGs

从表4可以看出，随着DG渗透率的增加，需求侧资源与SOP联合规划总成本呈现先下降后上升的趋势．

当DG渗透率较低时，配电系统主要通过上级电源进行供电，网络损耗相对较大．此时可平移负荷调度空间非常有限，需求侧资源无法得到充分利用，其管理费用不高．配电系统主要通过SOP配置实现馈线间功率平衡和系统内运行优化，则SOP成本相对较大．

随着DG渗透率的提高，分布式电源的功效开始得到发挥，网络损耗逐渐下降．同时需求侧资源中的可平移负荷占比逐渐增加，配电系统对SOP的依赖程度逐渐降低，所以需求侧资源管理成本上升，SOP配置成本下降．

当DG渗透率达到无法被完全消纳的程度时，为保证系统安全运行，部分新能源发电将被弃置，网络损耗也不再发生明显变化．同时，为了尽可能提高新能源消纳的程度，需求侧资源管理成本与SOP配置成本都有所增加．

4.4 置信度灵敏度分析

为分析模糊机会约束置信度和目标悲观值置信度在不同取值时对规划成本产生的影响，本文在方案1的基础上进行置信度灵敏度分析，得到需求侧资源成本和网损成本随两种置信度变化的关系曲线，分别如图3和图4所示．

图3 需求侧资源管理成本与置信度的关系

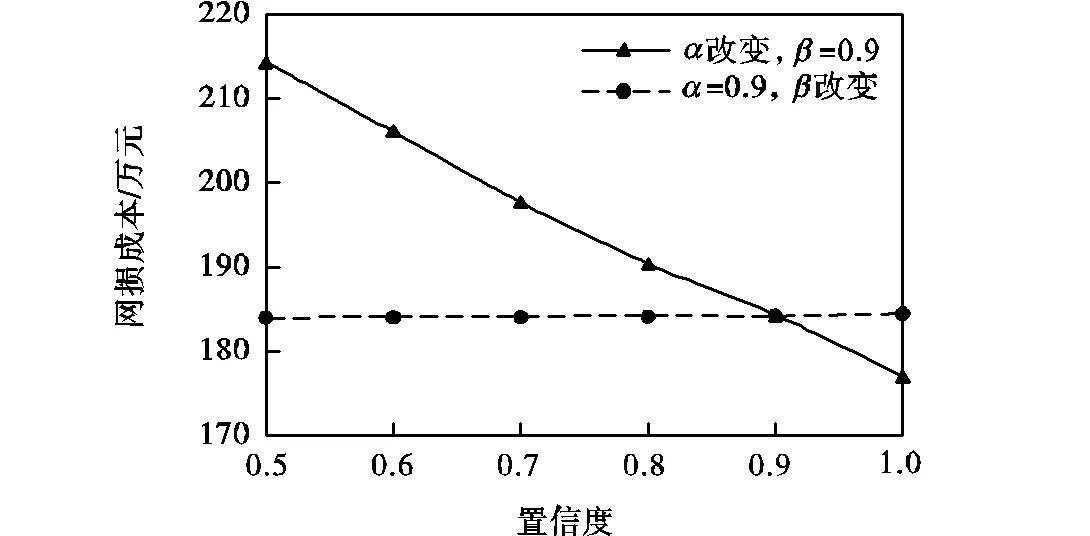
图4 网损成本与置信度的关系

由图3和图4可知，的改变对网损成本影响较大，对需求侧资源成本影响较小．为节点功率平衡的置信度，其数值将直接影响节点注入功率进而影响潮流计算的网络损耗功率，所以网损成本变化明显；但的改变对需求侧资源规划容量和调度功率而言影响较小，需求侧资源总成本变化不大．同时，值越大，节点注入功率的波动性越小，用户响应结果与配电公司最优调度可能存在的偏差越小，配电系统的网络损耗越小．

与相反，的改变对需求侧资源成本影响较大，对网损成本影响较小．为可削减负荷电量成本悲观值的置信度，其数值变化直接影响对需求侧资源的投入成本；但变化时需求侧资源规划容量基本不发生变化，且对潮流方程无直接影响，所以网损成本变化很小．

4.5 算法效果对比分析

为验证本文提出的模型处理方法对于求解SOP优化配置问题的有效性，在方案2中分别对比以下两种求解方法．

(1) 规划与运行交替优化，规划层采用粒子群算法，运行层采用CPLEX求解．

(2) 模型通过等效替代和多面体线性化处理转化为混合整数线性规划，整体采用CPLEX求解．

算法的求解时间和迭代次数如表5所示，收敛性能如图5所示．

表5 不同方法计算时间对比

Tab.5 Comparison of solving time using various methods

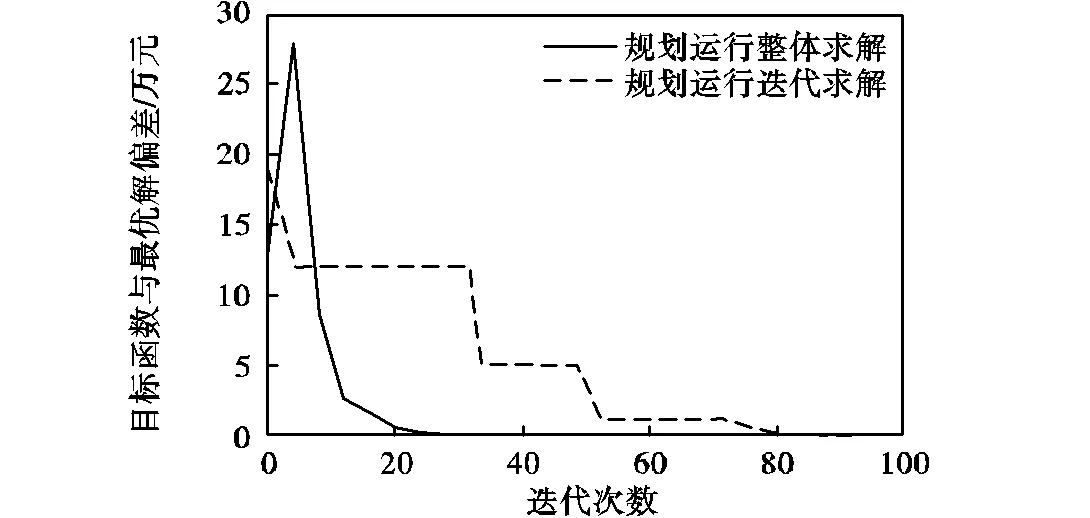
图5 算法性能对比

可以看出，本文所提出的将模型转化为混合整数线性规划并整体采用CPLEX求解的方法较规划与运行交替优化求解而言，在保证结果唯一性和全局最优性的前提下，具有更高效的求解效率．

5 结 论

(1) 需求侧资源与软开关的联合规划实现了不同规划对象的优势互补和资源重组，提高了规划方案的经济性．

(2) 通过需求侧资源与软开关的协同作用，降低了配电系统的网络损耗，提高了分布式电源的消纳能力，对建设灵活可控的配电网具有积极效益．

(3) 对原模型进行等效替代和多面体线性化处理后，可以直接采用CPLEX求解器进行求解．该方法在保证结果唯一性和全局最优性的同时，也提高了模型求解效率．

［1］ 王成山，宋关羽，李 鹏，等. 基于智能软开关的智能配电网柔性互联技术及展望[J]. 电力系统自动化，2016，40(22)：168-175.

Wang Chengshan，Song Guanyu，Li Peng，et al. Research and prospect for soft open point based flexible interconnection technology for smart distribution network [J]. Automation of Electric Power System，2016，40(22)：168-175(in Chinese).

［2］ 余贻鑫. 面向21世纪的智能电网[J]. 天津大学学报(自然科学与工程技术版)，2020，53(6)：551-556.

Yu Yixin. A brief description of the basics of the smart grid [J]. Journal of Tianjin University(Science and Technology)，2020，53(6)：551-556(in Chinese).

［3］ Wang Chengshan，Song Guanyu，Li Peng，et al Optimal siting and sizing of soft open points in active electrical distribution networks[J]. Applied Energy，2017，189：301-309.

［4］ 赵金利，陈 昊，宋关羽，等. 考虑可靠性收益的配电网智能软开关规划方法[J]. 电力系统自动化，2020，44(10)：22-31.

Zhao Jinli，Chen Hao，Song Guanyu，et al. Planning method of soft open point in distribution network considering reliability benefits[J]. Automation of Electric Power System，2020，44(10)：22-31(in Chinese).

［5］ Zhang Lu，Shen Chen，Chen Ying，et al. Coordinated allocation of distributed generation，capacitor banks and soft open points in active distribution networks considering dispatching results[J]. Applied Energy，2018，231：1122-1131.

［6］ 陈垚煜，耿光超，江全元，等. 考虑传统调控手段的配电网SOP选址定容方法[J]. 高电压技术，2020，46(4)：1181-1189.

Chen Yaoyu，Geng Guangchao，Jiang Quanyuan，et al. Optimal siting and sizing method of soft open point in distribution network combined with traditional regulations[J]. High Voltage Engineering，2020，46(4)：1181-1189(in Chinese).

［7］ 马 丽，薛 飞，石季英，等. 有源配电网分布式电源与智能软开关三层协调规划模型[J]. 电力系统自动化，2018，42(11)：86-93.

Ma Li，Xue Fei，Shi Jiying，et al. Tri-level coordinated planning model of distributed generator and intelligent soft open point for active distribution network[J]. Automation of Electric Power System，2018，42(11)：86-93(in Chinese).

［8］ Bai Linquan，Jiang Tao，Li Fangxing et al. Distributed energy storage planning in soft open point based active distribution networks incorporating network reconfiguration and DG reactive power capability[J]. Applied Energy，2018，21：1082-1091.

［9］ Huang Wujing，Zhang Ning，Kang Chongqing，et al. From demand response to integrated demand response：Review and prospect of research and application[J]. Protection and Control of Modern Power Systems，2019，4(2)：148-150.

［10］ 齐 宁，程 林，田立亭，等. 考虑柔性负荷接入的配电网规划研究综述与展望[J]. 电力系统自动化，2020，44(10)：193-207.

Qi Ning，Cheng Lin，Tian Liting，et al. Review and prospect of distribution network planning research considering access of flexible load[J]. Automation of Electric Power System，2020，44(10)：193-207(in Chinese).

［11］ 章 博，刘晟源，林振智，等. 高比例新能源下考虑需求侧响应和智能软开关的配电网重构[J]. 电力系统自动化，2021，45(8)：86-94.

Zhang Bo，Liu Shengyuan，Lin Zhenzhi，et al. Reconfiguration of distribution network with high proportion of renewable energy considering demand response and soft open point[J]. Automation of Electric Power System，2021，45(8)：86-94(in Chinese).

［12］ 王成山，宋关羽，李 鹏，等. 考虑分布式电源运行特性的有源配电网智能软开关SOP规划方法[J]. 中国电机工程学报，2017，37(7)：1889-1897.

Wang Chengshan，Song Guanyu，Li Peng，et al. Optimal configuration of soft open point for active distribution network considering the characteristics of distributed generation[J]. Proceedings of the CSEE，2017，37(7)：1889-1897(in Chinese).

［13］ 葛少云，周晨曦，刘 洪，等. 考虑环间接入模式及可靠性影响的有源配电网软开关规划[J]. 电力系统自动化，2021，45(8)：120-128.

Ge Shaoyun，Zhou Chenxi，Liu Hong，et al. Soft open point planning for active distribution network considering influence of access mode between feeder loops and reliability[J]. Automation of Electric Power System，2021，45(8)：120-128(in Chinese).

［14］ 叶雨晴，马 啸，林湘宁，等. 基于动态GA编码的柔性多状态开关选址策略[J]. 高电压技术，2020，46(4)：1171-1181.

Ye Yuqing，Ma Xiao，Lin Xiangning，et al. Study on site selection of soft open points based on dynamic GA coding strategy[J]. High Voltage Engineering，2020，46(4)：1171-1181(in Chinese).

［15］ 程 林，齐 宁，田立亭，等. 考虑运行控制策略的广义储能资源与分布式电源联合规划[J]. 电力系统自动化，2019，43(10)：27-35，43.

Cheng Lin，Qi Ning，Tian Liting，et al. Joint planning of generalized energy storage resource and distributed generator considering operation control strategy[J]. Automation of Electric Power System，2019，43(10)：27-35，43(in Chinese).

［16］ 孙宇军，王 岩，王蓓蓓，等. 考虑需求响应不确定性的多时间尺度源荷互动决策方法[J]. 电力系统自动化，2018，42(2)：106-113，159.

Sun Yujun，Wang Yan，Wang Beibei，et al. Multi-time scale decision method for source-load interaction considering demand response uncertainty[J]. Automation of Electric Power System，2018，42(2)：106-113，159(in Chinese).

［17］ 王成山，孙充勃，李 鹏，等. 基于SNOP的配电网运行优化及分析[J]. 电力系统自动化，2015，39(9)：82-87.

Wang Chengshan，Sun Chongbo，Li Peng，et al. SNOP-based operation optimization and analysis of distribution networks[J]. Automation of Electric Power System，2015，39(9)：82-87(in Chinese).

［18］ 薛 飞，马 丽，朱 昊，等. 柔性配电网中考虑SOP优化的分布式电源双层规划[J]. 电力系统及其自动化学报，2020，32(8)：109-115.

Xue Fei，Ma Li，Zhu Hao，et al. Bi-level programming of distributed generations in flexible distribution network with SOP optimization[J]. Proceedings of the CSU-EPSA，2020，32(8)：109-115(in Chinese).

［19］ 于 浩，刘家恺，宋关羽，等. 基于二阶锥规划的有源配电网多时段负荷恢复方法[J]. 天津大学学报(自然科学与工程技术版)，2019，52(12)：1303-1311.

Yu Hao，Liu Jiakai，Song Guanyu，et al. Multi-time-period load restoration method for active distribution networks based on SOCP[J]. Journal of Tianjin University(Science and Technology)，2019，52(12)：1303-1311(in Chinese).

［20］ 熊 虎，向铁元，陈红坤，等. 含大规模间歇式电源的模糊机会约束机组组合研究[J]. 中国电机工程学报，2013，33(13)：36-44.

Xiong Hu，Xiang Tieyuan，Chen Hongkun，et al. Research of fuzzy chance constrained unit commitment containing large-scale intermittent power[J]. Proceedings of the CSEE，2013，33(13)：36-44(in Chinese).

［21］ 郭清元，吴杰康，莫 超，等. 基于混合整数二阶锥规划的新能源配电网电压无功协同优化模型[J]. 中国电机工程学报，2018，38(5)：1385-1396.

Guo Qingyuan，Wu Jiekang，Mo Chao，et al. A model for multi-objective coordination optimization of voltage and reactive power in distribution networks based on mixed integer second-order cone programming[J]. Proceedings of the CSEE，2018，38(5)：1385-1396(in Chinese).

［22］ 贺帅佳，高红均，刘俊勇，等. 计及需求响应柔性调节的分布鲁棒DG优化配置[J]. 中国电机工程学报，2019，39(8)：2253-2264.

He Shuaijia，Gao Hongjun，Liu Junyong，et al. Distributionally robust optimal DG allocation model considering flexible adjustment of demand response[J]. Proceedings of the CSEE，2019，39(8)：2253-2264(in Chinese).

［23］ 刘洪，郑 楠，葛少云，等. 内嵌需求响应与优化运行策略的主动配电系统源网协同规划[J]. 电力系统自动化，2020，44(3)：89-97.

Liu Hong，Zheng Nan，Ge Shaoyun，et al. Coordinated planning of source and network in active distribution system with demand response and optimized operation strategy[J]. Automation of Electric Power System，2020，44(3)：89-97(in Chinese).

［24］ 高红均，刘俊勇. 考虑不同类型DG和负荷建模的主动配电网协同规划[J]. 中国电机工程学报，2016，36(18)：4911-4922，5115.

Gao Hongjun，Liu Junyong. Coordinated planning considering different types of DG and load in active distribution network[J]. Proceedings of the CSEE，2016，36(18)：4911-4922，5115(in Chinese).

Coordinated Planning of Soft Open Points and Demand-Side Resources Considering an Elastic Response

Ge Shaoyun1，Li Junkai1，Liu Hong1，Wang Liyong2，Wang Pengxiang3，Wang Chengshan1

(1. Key Laboratory of Smart Grid of Ministry of Education，Tianjin University，Tianjin 300072，China；2. State Grid Beijing Electric Power Company，Beijing 100031，China；3. Power China Henan Electric Power Engineering Co. Ltd.，Zhengzhou 450007，China)

This study proposes a coordinated planning model of soft open points and demand-side resources，which consider the uncertainty of load shifting and reducing responses. First，based on the load-type analysis，a triangular membership fuzzy model is constructed to describe the uncertainty of various response modes. Second，a fuzzy chance-constrained planning model is established to minimize the comprehensive cost of the distributed system operator. This cost includes the capital cost of the demand-side resources and soft open points，energy-loss costs，and the abandonment cost of distributed generators(DGs). Third，based on the transformation of fuzzy variables，equivalent substitution，and the polyhedral linearization technique，the fuzzy chance-constrained second-order cone-programming model is transformed into a mixed-integer linear programming model，which can be solved by business solvers directly. Finally，the proposed model’s effectiveness is verified using a power distribution system from northern China. The result demonstrates that the co-optimization model helps realize complementary advantages of demand-side resources and soft open points. This model not only guarantees the economy of planning schemes but also improves the DG accommodation.

soft open point；demand-side resource；fuzzy chance-constrained planning；polyhedral linearization

10.11784/tdxbz202104046

TM715

A

0493-2137(2022)05-0462-09

2021-04-22；

2021-11-01.

葛少云（1964—  ），男，博士，教授，syge@tju.edu.cn.

刘 洪，liuhong@tju.edu.cn.

国家自然科学基金委员会-国家电网公司智能电网联合基金资助项目(U1866207).

Supported by the National Natural Science Foundation of China-State Grid Joint Fund for Smart Grid(No. U1866207).

(责任编辑：孙立华)