轮胎-路面三维力解析模型的建立与简化方法

刘庆纲，宋皓杰，郭 昊，魏旭明，周兴林

轮胎-路面三维力解析模型的建立与简化方法

刘庆纲1，宋皓杰1，郭 昊1，魏旭明1，周兴林2

(1. 天津大学精密测试技术及仪器国家重点实验室，天津 300072；2. 武汉科技大学交通学院，武汉 430081)

研究轮胎-路面之间的三维作用力，对预测路面早期损坏、优化道路设计具有指导作用，同时也是分析车辆动力学性能、研制和改进整车控制系统的有效手段．文中利用ABAQUS有限元仿真软件，建立了轮胎与路面之间相互作用力与胎冠相对轮辋中心位移之间的力-位移多元非线性回归模型；该模型通过分析在三维力作用下轮胎不同位置处节点的变形和位移，实现了不同节点处的轮胎与路面之间作用力的求解，并通过改变充气断面尺寸、不同载荷下沉量等指标使模型有效性得到了验证，为设计并优化位移传感器的布局、提高测量结果的可信度，提供了理论依据．采用带有二次项的多元非线性回归模型对11.00R20载重子午线轮胎进行仿真计算．结果表明，在接地中心角不超过±15°范围内，回归模型的三维力预测值相对于预设值的误差不超过±2%．为在兼顾回归模型准确度的前提下，提高该模型的解算效率、降低由位移解算力过程的繁琐性，通过分析完整模型中各子项对力预测结果的贡献度，进一步提出了简化回归模型；当≤±15°时，各个节点处完整模型与简化模型均方根误差(RMSE)的最大值相差0.43kN；当≤±9°时，两者差值减小至0.27kN．分析结果表明，通过对安装在轮胎上的位移传感器所采集的数据进行处理，完整模型和简化模型均能实现轮胎与路面间相互作用三维力的预测和计算，但简化模型的适用范围比完整模型要窄．

轮胎有限元仿真建模；轮胎-路面；三维力模型；多元回归分析；模型简化

据统计，我国道路特别是高速公路的设计使用年限一般为15年，但实际平均使用年限仅为5～7年[1].沥青路面结构在道路开通后会出现车辙、裂缝、松动、沉降等问题，严重危及路面的使用性能和安全性能[2]．若采用简单的平均垂直载荷的道路力学设计模型，无法测量轮胎与路面接触的三维力动载荷及其分布，则局限性十分明显，特别是对于重载车辆而言[3-5].为了实现轮胎接地特性和运行状态的监控、路面早期破坏形式的预测和预防，通常需要同时对三维力及其应力分布状况进行实时测量．

为了准确分析沥青路面在车辆荷载作用下的应力分布，许多学者利用有限元软件建立了三维轮胎-路面接触模型，模拟动载作用下路面的三维力分布，并由此分析了沥青路面结构的损伤与灾害机理[6-11].一些研究人员正在研制三维位移-力传感器，分析轮胎与路面矢量接触力作用下位移与力的关系[12-16].以上研究的重点都注重于传感器自身结构的仿真方法开发上，缺乏对传感器分布的合理性和力解耦方案的相关分析和研究．

为了解决上述问题，本文通过对轮胎-路面相互作用下轮胎变形-位移-应力的非线性多元回归建模，研究传感器优化分布，提高测量结果的可靠性，并对简化分析模型进行了研究和分析．

1 轮胎的有限元模型建模与分析

1.1 有限元建模

以11.00R20全钢载重子午线轮胎[17]为例，利用ABAQUS有限元仿真软件，以参数化建模方法进行建模分析．11.00R20子午线轮胎断面材料分布如图1(a)所示，由于轮胎三维模型具有旋转对称性，二维轴对称模型经二维轴对称网格后，可绕中性轴旋转360°生成轮胎三维模型，如图1(b)所示．

图1 轮胎材料分布

轮辋和地面都定义为解析刚体，轮辋与胎圈的接触对简化为绑定约束．在地面参考点作用竖直位移，使轮胎与地面建立好接触关系，再在地面参考点作用特定大小的集中力，即可模拟轮胎与路面之间的作用力．图1(c)是在标准充气压力930kPa、标准载荷3550kg条件下轮胎的轮廓变形情况示意．图1(c)中的表示模型中轮胎内衬层中心圆上某点和接地中心点分别与轮胎旋转中心点连线之间的夹角．在标准气压930kPa下，记录不同载荷下的轮胎下沉量仿真计算数值，绘制出载荷与下沉量的关系曲线，如图2(a)所示，这与文献[18]中给出的实测数据曲线吻合程度较好，证明了轮胎有限元模型的有效性．

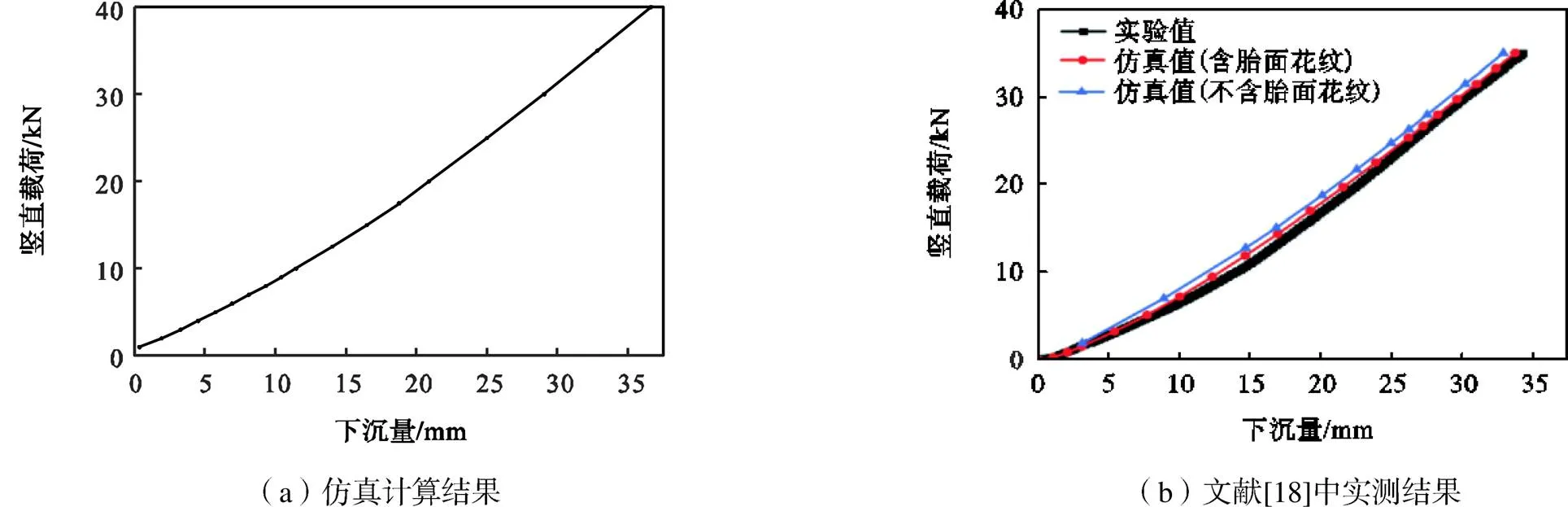
图2 930kPa内压下沉量与载荷关系

1.2 轮胎模型有效性分析

为了验证轮胎模型的有效性，将轮胎在充气工况和静载荷工况下的仿真计算数值与实测结果进行比对．表1是标准气压930kPa、标准负荷3550kg工况下的模拟值与实测值[19]的对比，可发现以实测值为标准的各项测试参数模拟值的相对误差最大不超过3.15%，证明了模型的有效性．

表1 模拟仿真数据与实测数据对比

Tab.1 Comparison of simulation and measured data

在标准气压930kPa下，垂直载荷与下沉量的关系曲线与文献[18]中给出的实测数据曲线吻合程度较好，如图2(b)所示，进一步证明了本文轮胎模型的有效性．

2 三维力的统计模型的建立

为了得到轮胎-路面三维力与轮胎上内衬层中心圆任意一点处位移的函数关系，进而得到由传感器实测的位移值解算三维力的方案，用有限元仿真计算的方法获得不同力(建模时共用了61组)作用下的位移，以此作为样本，用最小二乘多元回归拟合的方法，建立力与位移关系式．考虑到轮胎材料非线性、力与位移的维间耦合等因素，函数拟合公式为

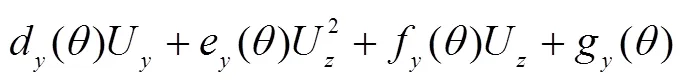
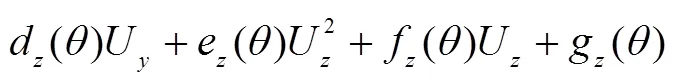
式中：F、F、F为轮胎-路面作用力的3个分量，kN；U、U、U为轮胎内衬层中心圆上某一点处的位移的3个分量，mm；a()、b()、c()、d()、e()、f()、g()(、、)均为拟合系数．给定节点位置参数的条件下，F(或F，F)可由U、U、U结合拟合系数解得．

轮胎内衬层中心圆上非节点处的位移无法依据有限元模型求得，故其位移与轮胎-路面三维力之间的函数关系并不能采用回归拟合的方式得到．这些非节点处的力与位移函数关系中的系数可用邻近节点处的系数做线性内插的方法进行估计．为了检验拟合结果的准确度，计算各个节点处拟合结果的均 方根误差(RMSE)和决定系数2，计算结果如图3所示．

由图3可知，越接近0°，即位移传感器的安装位置越接近轮辋中心，则回归方程的RMSE值越小，R值越大．

为了评估每个节点的解耦关系的准确性，选择了5个附加的三维力预设作为计算每个节点位移的测试条件，利用回归模型，将位移值代入力-位移拟合关系，得到三维力预测值，预测值与预设值的相对误差如图4所示．结果表明，随变化的三维力预测误差在中间较小两侧较大；当≤±15°时，各方向力的预测误差除最后1组测试条件中的F外，其他值均不超过2%．

图3 各节点处回归模型的RMSE和R2

图4 三维力预测误差与节点位置的关系

3 三维力-位移的统计模型的简化

以式(1)～式(3)的函数形式对力与位移的关系式进行回归分析，计算结果表明，这种各个变量都具备二次项的函数形式能比较准确地反映轮胎系统受三维力作用下的非线性特性和力的耦合特性．然而，由于所选函数形式的复杂性，用位移计算力的过程较为繁琐，这给轮胎系统的标定和力的解耦带来诸多麻烦，也不利于测量系统误差的理论分析．因此，在保证回归模型精度的前提下，应选取更简单的方程来描述力与位移的数学关系．原有的回归模型中，采用了位移3分量各自的二次函数之和的形式来表示某一方向上的力，关系式中共具备7项，在用该模型进行三维力的预测时，当某一项的计算结果在力的预测值中占比远小于其他项时，便可认为该项对预测结果的贡献可以忽略不计．也就是说，该项的有无对最终的预测结果影响很小，故力与位移函数关系可以用式(1)～式(3)中删除这些项之后的形式来进行描述．为了找到那些对力的预测结果贡献较小的项，以F的预测结果为例，定义各项的贡献系数分别为

贡献系数表示了回归模型中某一项对总体预测结果的贡献程度，其绝对值越大则说明该项对预测结果的影响越明显，在回归模型中的地位越重要．以F＝5kN、F＝5kN、F＝20kN的轮胎三维力作为仿真测试条件，用有限元仿真计算出该工况下轮胎模型上各节点处的位移，再将各节点的位移值分别代入各自的回归方程中计算力的预测值以及各项的贡献系数．计算结果如图5所示．

分析计算结果可知，在各个节点处，F回归方程中的各项贡献系数中，起主导作用的是(U)、(U)、(const)这3项，其余项很接近0，故可忽略不计；F回归方程中的各项贡献系数中，起主导作用的是(U)、(U)这2项；F回归方程中的各项贡献系数中，起主导作用的是(U2)、(U)、(const)这3项．在力与位移关系的完整回归模型中保留上述主导项，可以得到力与位移的简化回归模型如下．

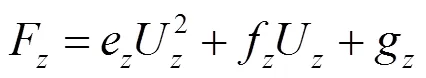
由式(4)～式(6)可知，F被视为关于U和U的线性函数，F被视为关于U和U的线性函数，F被当视为仅关于U的二次函数．因此，这种简化的回归模型在一定程度上忽略了轮胎系统的非线性特性和力的维间耦合效果，因此对真实的轮胎系统力学特性的描述不如完整的回归模型准确．

为了对简化回归模型的准确程度做出评价，这里采用第2节中类似的方法，由于式(5)的回归模型中不带截距项，不能保证决定系数2的计算结果在0～1之间，此时该指标失效，故这里仅通过计算各个节点处简化回归方程的RMSE来评价回归模型的精度，并与完整回归模型的评价参数比较，计算结果如图6所示．

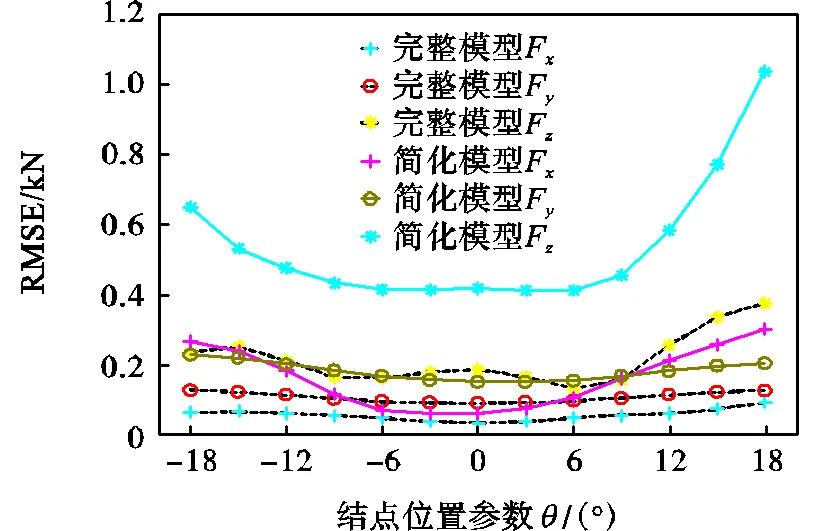
图6 简化模型与完整模型的均方根误差

从图6可以看出：①简化回归模型的均方根误差大于完全回归模型的均方根误差，且差异显著．②两种模型的RMSE均随节点位置参数绝对值的增大而增大，但简化模型的RMSE受节点位置的影响更明显．在简化模型中，超过±10°以后RMSE的变化已经很明显，但完整模型能在不超过±18°的范围内保证RMSE变化不大，这说明简化模型对节点位置要求更严格，只能在接地中心附近的小范围内保证高精度．更具体的数据表明，在简化回归模型中RMSE变化不明显的±9°范围内的7个节点上，F、F和F的RMSE最大值分别为0.1605kN、0.1850kN和0.4560kN．

以F、F和F的最大值(25.0kN、17.2kN、50.0kN)为量程，在99.7%的置信水平下，回归方程拟合误差引入的最大满量程相对误差(3倍RMSE)分别为1.93%、3.15%和2.74%．当≤15°时，完整回归模型与简化回归模型的RMSE最大值相差0.43kN，当≤9°时，其差值降至0.27kN．

利用两个回归模型得到的力与位移关系预测三维力值，计算预测值与预设值的相对误差．以F＝5kN、F＝5kN、F＝20kN作为仿真测试条件，用有限元仿真模拟结果得到的13个节点位移值作为测试样本．计算结果表明，在各个节点处F、F和F的最大预测误差分别是-3.81%、-7.28%、-2.86%．简化回归模型在一定程度上是有效的，可以应用于对力的预测精度要求不高的情况．原有完整模型的表达式形式复杂，包含的参数多，每个方向上的力均需要3个方向位移方可解算．由式(4)～式(6)可知，在进行简化后，仅需U和U即可解算F，仅需U和U即可解算F，仅需U和U这即可解算F．在只需要解算某一方向力时，不必测出所有方向上的位移，这有效降低了位移传感器的性能要求和测量系统的实现难度．

4 结 语

采用多元非线性回归模型建立了轮胎三维力与各节点位移之间的数学关系．为了提高拟合精度，应当增加输入回归模型的样本数量，并且采用项数较多、形式复杂的的拟合函数形式来进行回归分析．

通过分析完整模型中各子项对力预测结果的贡献，进一步提出了简化的回归模型，在保证预测误差基本相同的前提下，提高了模型的计算效率．当不超过±9°时，完整模型和简化模型各节点处回归模型的RMSE最大值之差为0.27kN，该差值随着的增大而增大．通过对安装在轮胎上的位移传感器数据的分析表明，完整模型和简化模型都能实现轮胎与路面间三维力的预测和计算，但简化模型的适用范围比完整模型收窄．

本文虽然是对重载卡车的轮胎-路面作用力提出的完整解析模型和简化解析模型，利用位移数据用于解算和预测三维作用力，但该方法对其他种类轮胎的相关分析仍适用；根据作用力的解析结果与接地角之间的关系，在进一步提高传感器安装位置合理性的同时，有助于确认轮胎对路面作用力的性质和作用特点以及对道路产生损伤的方式，为道路安全设计提供分析依据．

［1］ 王晓飞. 水泥混凝土路面裂缝扩展机理及磨细矿渣改性水泥裂缝修补材料研究[D]．西安：长安大学， 2005.

Wang Xiaofei. Study on Crack Propagation Mechanism of Cement Concrete Pavement and Modified Cement Crack Repair Material with Grinding Slag[D]. Xi’an： Chang’an University，2005 (in Chinese).

［2］ 崔新壮，黄 丹，薛 强，等. 沥青路面病害力学研究进展[J]. 山东大学学报(工学版)，2016，46(5)：68-87.

Cui Xinzhuang，Huang Dan，Xue Qiang，et al. A review of mechanics of asphalt pavement disease[J]. Journal of Shandong University(Engineering Sci-ence)，2016，46(5)：68-87(in Chinese).

［3］ 李金辉，何 杰，李旭宏. 车辆随机及移动荷载作用下路面动态响应[J]. 长安大学学报(自然科学版)，2015，35(2)：38-45.

Li Jinhui，He Jie，Li Xuhong. Dynamic response of pavement under vehicle random load and moving constant load[J]. Journal of Chang’an University(Natural Science Edition)，2015，35(2)：38-45(in Chinese).

［4］ 陈 洋，戴宗宏，陈焕明，等. 车辆多伦随机动载作用下柔性沥青路面的应变分析[J]. 振动与冲击，2016，35(19)：15-19，44.

Chen Yang，Dai Zonghong，Chen Huanming，et al. Strain analysis of a flexible asphalt pavement under multi-wheel random dynamic loads of vehicles[J]. Journal of Vibration and Shock，2016，35(19)：15-19，44(in Chinese).

［5］ 郭红兵，王 宁，吕光印. 轮胎-沥青路面接触效应数值分析[J]. 郑州大学学报(工学版)，2011，32(1)：34-37.

Guo Hongbing，Wang Ning，Lü Guangyin. Numerical analysis on contact effect of tire-asphalt pavement structure[J]. Journal of Zhengzhou University(Engineering Science)，2011，32(1)：34-37(in Chinese).

［6］ 李雪连，陈宇亮，张起森. 高温条件下上坡路段沥青路面结构性能研究[J]. 公路交通科技，2010，27(8)：1-6.

Li Xuelian，Chen Yuliang，Zhang Qisen. Study on performance for upslope asphalt pavement structure at high temperature[J]. Journal of Highway and Transportation Research and Development，2010，27(8)：1-6(in Chinese).

［7］ 崔亚楠，邢永明，倪文琛. 基于细观结构特征的沥青混合料断裂机理研究[J]. 建筑材料学报，2013，16(1)：86-90.

Cui Yanan，Xing Yongming，Ni Wenchen. Study on split mechanism of asphalt mixture based on meso-structure feature[J]. Journal of Building Materials，2013，16(1)：86-90(in Chinese).

［8］ 张小龙，张为公. 轮力传感器及其在汽车道路试验中的应用[J]. 仪表技术与传感器，2005(1)：4-6，9.

Zhang Xiaolong，Zhang Weigong. Wheel force transducer and its application in motor vehicle road test[J]. Instrument Technique and Sensor，2005(1)：4-6，9(in Chinese).

［9］ 商 亮. 具有运动感知能力的车轮力传感器设计与实现[D]. 南京：东南大学，2018.

Shang Liang. The Design and Implementation of Wheel Force Transducer with Motion Perception Ability[D]. Nanjing：Southeast University，2018(in Chinese).

［10］ Tuononen A J. On-board estimation of dynamic tyre forces from optically measured tyre carcass deflections[J]. International Journal of Heavy Vehicle Systems，2009，16(3)：362-378.

［11］ Tuononen A J. Laser triangulation to measure the carcass deflections of a rolling tire[J]. Measurement Science & Technology，2011，22(12)：125304-1253011.

［12］ Cheli F，Braghin F，Brusarosco M，et al. Design and testing of an innovative measurement device for tyre-road contact forces[J]. Mechanical Systems and Signal Processing，2011，25(6)：1956-1972.

［13］ Ise T，Higuchi M，Tachiya H. Development of a tactile sensor to measure tire friction coefficients in arbitrary directions[J]. International Journal of Automation Technology，2013，7(3)：359-366.

［14］ 赵 健，路妍晖，朱 冰，等. 内嵌加速度计的智能轮胎纵/垂向力估计算法[J]. 汽车工程，2018，40(2)：137-142，183.

Zhao Jian，Lu Yanhui，Zhu Bing，et al. Estimation algorithm for longitudinal and vertical forces of smart tyre with accelerometer embedded[J]. Automotive Engineering，2018，40(2)：137-142，183(in Chinese).

［15］ Chen Zhao，Xie Zhipeng，Zhang Jian. Measurement of vehicle-bridge-interaction force using dynamic tire pressure monitoring[J]. Mechanical Systems and Signal Processing，2018，104(6)：370-383.

［16］ Wang Haoqi，Nagayama Tomonori，Su Di. Estimation of dynamic tire force by measurement of vehicle body responses with numerical and experimental validation [J]. Mechanical Systems and Signal Processing，2019，123(5)：369-385.

［17］ GB/T 2977—2016 载重汽车轮胎规格、尺寸、气压与负荷[S]. 北京：中国标准出版社.

GB/T 2977—2016 Size Designation，Dimensions，Inflation Pressure and Load Capacity for Truck Tyres [S]. Beijing：National Standard of People’s Republic of China(in Chinese).

［18］ Wang Wei，Yan Shan，Zhao Yayuan. Numerical and experimental studies of a radial truck tire with tread pattern[J]. Simulation，2015，91(11)：970-979.

［19］ 赵亚元，王 伟. 载重子午线轮胎胎面磨耗有限元分析[J]. 橡胶工业，2016，63(7)：421-424.

Zhao Yayuan，Wang Wei. Finite element analysis on tread wear of truck radial tyre[J]. Rubber Industry，2016，63(7)：421-424(in Chinese).

Establishment and Simplification of Tyre-Pavement 3D Force Analysis Model

Liu Qinggang1，Song Haojie1，Guo Hao1，Wei Xuming1，Zhou Xinglin2

(1. State Key Laboratory of Precision Measurement Technology and Instruments，Tianjin University，Tianjin 300072，China；2. School of Communications，Wuhan University of Science and Technology，Wuhan 430081，China)

The study of the three-dimensional vector value force(3D force) between the tyre and pavement can guide the prediction of early pavement damage and optimize road design. It is also an effective method for analyzing dynamic vehicle performance and develop and improve vehicle control systems. The multivariate nonlinear regression model of the 3D force-displacement，which means the displacement of the tire crown relative to the center of the rim，is established using the ABAQUS finite element simulation software. The model is able to realize the solution of the deformation force by analyzing the deformation/displacement at different node positions. By changing the size of the inflatable section and the sinking amount of different loads，its validity is obtained. This provides a theoretical basis for designing and optimizing the layout of displacement sensors and improving the reliability of measurement results. The multivariate nonlinear regression model with a quadratic term is applied to the simulation results of the 11.00 R20 loaded radial tyre. Experimental results show that the error of the regression model relative to the preset 3D force is less than ±2% within the grounding center angle≤±15°. A simplified regression model is further proposed by analyzing the contribution of each item in the complete model to the force prediction results to improve the efficiency of the regression model and reduce the complexity of the process of the displacement calculation. The maximum difference of the root mean square error(RMSE) between the predictive value and the preset value of the 3D force of the complete model and simplified model on each node is 0.43kN when≤±15° and 0.27kN whenis ≤±9°. The analyses show that both the complete and simplified models can realize the prediction and calculation of the 3D force between the tyre and pavement by analyzing the data of the displacement sensor installed on the tyre. However，the application range of the simplified model is narrower than that of the complete one.

modeling of tyre finite element simulation；tyre-pavement；3D force model；multiple regression analysis；model simplification

10.11784/tdxbz202102010

TQ366.1

A

0493-2137(2022)05-0512-07

2021-02-05；

2021-03-15.

刘庆纲（1964—  ），男，博士，教授．

刘庆纲，lqg@tju.edu.cn.

国家自然科学基金-国家重大科研仪器研制资助项目(51827182).

Supported by the National Natural Science Foundation of China-National Major Scientific Research Instrument Development Project (No.51827182).

(责任编辑：孙立华)