ARIMA模型和BP神经网络模型在广西老年人艾滋病发病率预测中的应用
2022-03-09卓小康郭振友
卓小康,郭振友
(桂林医学院人文与管理学院,广西 桂林 541000)
广西是我国艾滋病高发地区,相关统计显示[1],到2017 年10 月为止,生活在广西的艾滋病患者共计报告8 万多例。随着老龄化社会的发展,艾滋病传播流行呈现出新特征,其中以老年男性HIV 感染人数快速增长为显著特征之一[2-4],这充分表明老年人群现已成为艾滋病感染的高危群体。既往艾滋病预测研究主要以ARIMA 模型、灰色模型为主,用BP 神经网络模型的较少。因此,本研究基于ARIMA模型和BP 神经网络模型对2005-2017 年广西老年人艾滋病月发病率数据建立预测模型,并拟合形成最优预测模型,为制定老年人艾滋病防控政策、措施提供参考。
1 资料与方法
1.1 资料来源 相关数据来源于广西疾病预防控制中心法定传染病报告收集的广西艾滋病发病人数数据以及广西统计局2005-2017 年广西统计年鉴收集的广西总人口数据,进而计算得出广西壮族自治区2005-2017 年老年人艾滋病月发病率数据。
1.2 ARIMA 模型建模
1.2.1 数据预处理 将2005-2016 年广西老年人艾滋病月发病率形成包含144 个数据的时间序列,然后检验2005-2016 年广西老年人艾滋病月发病率时间序列的平稳性(图1)。因原始数据波动幅度较大,在2011 年达到最大值,序列明显不平稳,因此做差分使其平稳化,经过一阶差分后(图2),数据在一定范围内上下波动,相对稳定,视为平稳序列。

图1 差分前时间序列图

图2 差分后时间序列图
1.2.2 模型识别 根据自相关图和偏自相关图,判断样本p 值和q 值,通过显示出来的特点,将全部可能的模型进行拟合与建模,综合各个模型的统计量、AIC、BIC 等值进行比较,最终选择最佳模型。
1.2.3 模型检验 用白噪声检验判断模型的显著性,用参数检验判断参数的显著性[5]。若为非白噪声序列,说明模型不具代表性,需考虑拟合其他模型。反之,模型显著有效。
1.3 BP 神经网络模型建模
1.3.1 数据预处理 训练前使数据规范化,以快速获得最佳模型。2005-2017 年广西老年人艾滋病月发病率均大于1,不符合规范,予以归一化处理,将月发病率通过mapminmax 函数运算映射到[-1,1]区间。
1.3.2 确定参数 将2005-2016 年广西老年人艾滋病月发病率数据作为训练集,2017 年1 月-12 月广西老年人艾滋病月发病率数据作为测试集。用2005年1 月、2006 年1 月、2007 年1 月的广西老年人艾滋病月发病率预测2008 年1 月的广西老年人艾滋病月发病率,最后分别形成3×108 的输入矩阵和1×108 的输出矩阵。数据集分割之后,确定参数,如网络层数、各层神经元节点数、激活函数、目标误差、训练函数等[6,7]。
1.4 统计学方法 利用SPSS 26.0 统计学软件进行分析,借助R 4.0.3 软件完成ARIMA 模型建模,应用MATLAB 2018b 软件实现BP 神经网络模型建模及预测,应用WPS Excel 软件进行误差分析。采用均方误差(mean square error,MSE)、平均绝对误差(mean absolute error,MAE)和平均绝对误差百分比(mean absolute percent error,MAPE)3 个误差指标评价2个模型的预测效果,数值越小,表明模型预测效果越佳[8]。计数资料以(n)表示,采用字2检验。以P<0.05表示差异有统计学意义。
2 结果
2.1 ARIMA 建模结果
2.1.1 模型识别 使用auto.arima 函数进行ARIMA模型自动识别,R 软件根据函数自动的拟合所有可能的模型,筛选掉AIC 较大的模型,选出AIC 最小的模型为最优模型,即ARIMA(2,1,2)(2,0,0)12。
2.1.2 模型检验结果 模型检验结果中P值均大于0.05,属于白噪声序列,拟合模型有效。用P值函数对模型参数做t检验,结果显示6 个参数的P值均小于0.05,参数显著有效,该模型可定为最优模型,见表1。

表1 ARIMA 模型残差序列白噪声检验
2.2 BP 神经网络建模结果 经反复训练网络发现,隐含层节点数为9 时,训练函数用trainlm,目标误差为0.01,模型经过6 次迭代训练后误差达到目标值,模型决定系数R2=0.8858,此时训练得到的模型最优,即LM算法3-9-1 结构的BP 神经网络模型。
2.3 模型预测效果比较 利用训练好的ARIMA(2,1,2)(2,0,0)12模型和LM算法3-9-1 结构的BP 神经网络模型分别预测2017 年1 月-12 月广西老年人艾滋病发病率,结果显示两种模型的预测值与实际值趋势吻合,虚线、点线均在实线下方,见图3。与2017 年发病率的实际平均值相比,两种模型的预测平均值均小于实际平均值,但BP 神经网络模型预测值较接近实际,见表2。BP 神经网络模型的MSE=0.0822、MAE=0.2352、MAPE=0.1510%均小于ARIMA 模型的MSE=0.1198、MAE=0.3775、MAPE=0.2368%。
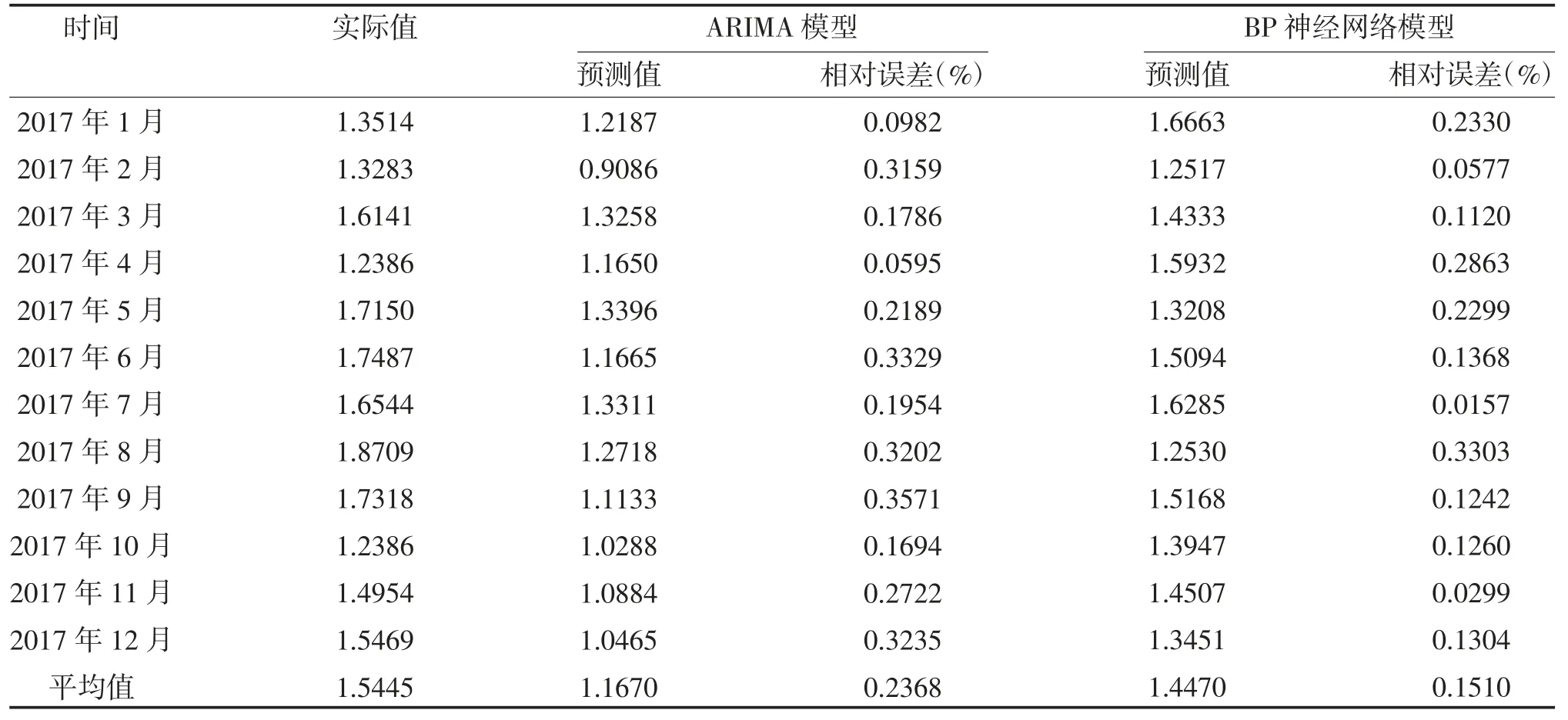
表2 ARIMA(2,1,2)(2,0,0)12 模型与LM算法3-9-1 结构的BP 神经网络模型预测比较

图3 2017 年预测值与实际值对比时序图
3 讨论
老年人是我国艾滋病流行新出现的重点人群,相关研究表明[9,10],广西老年人群艾滋病发病率较高,尤其是空巢老年男性以嫖娼感染为主。做好艾滋病疫情的监测,能助力建设健康中国和实现健康老龄化。目前关于各类传染病发病率预测的模型十分丰富,包括BP 神经网络模型、ARIMA 模型、GM(1,1)模型、Elman 模型、Prophet 模型、Spectrum/EPP模型等。
就模型的适用条件而言,ARIMA 模型和GM(1,1)模型都是传统的线性模型,前者要求数据资料是平稳的时间序列,可充分体现趋势性和季节性,同时也能把复杂的影响因素化繁为简,统一规划到时间变量中[11],以时间这一线性变量做研究,后者对于波动性较大数据不适用。Prophet 模型在ARIMA 模型的基础上加入了节日这一因素,适用于处理受节日影响的数据资料。受人脑神经元学习能力的启发出现了基于机器语言的人工神经网络,它不受主观因素的影响,并且能根据输入数据自主学习,具有极强的非线性映射能力。BP 神经网络模型是典型的非线性模型,对数据资料无特殊要求,更擅长处理数据资料中的非线性信息。Elman 模型是一种比BP 神经网络多一层承接层动态神经网络,使用范围更广。Spectrum/EPP 模型则是需要输入分类指标的艾滋病疫情预测模型[12]。就预测精度而言,郭玉秀[13]和程燕等[14]在发病率预测研究中发现,ARIMA 模型比GM(1,1)模型预测精度高。孙锦峰等[15]在流感发病率研究中发现,ARIMA 模型比Elman 模型精度高。李顺勇等[16]在艾滋病发病率研究中发现,Prophet 模型较ARIMA 模型的预测效果更优。陈远方等[17]在乙肝发病率研究中发现,当样本量较大时,ARIMA模型预测精度略高于BP 神经网络模型,反之BP神经网络模型精度更高。由此可见,在线性模型中ARIMA 模型预测效果更好,而BP 神经网络模型在小样本中具有良好的适用性。
本研究结果显示,广西老年人艾滋病月发病率是不稳定的,随着影响因素的变化而上下波动,其影响因素包括民族风俗习惯、交通发展水平、经济水平、人口流动、文化程度、国家方针政策及其它相关影响因素等[18-20],这些因素错综复杂,大部分以非线性关系形式存在,简单的线性模型难以解释清楚。综合模型的适用条件、预测精度和本文数据自身的特点进行双向选择,尝试选用传统的线性模型ARIMA模型和基于机器学习的非线性模型BP 神经网络模型对2005-2017 年广西老年人艾滋病月发病率进行研究,模型间形成对照,择优应用于广西老年人艾滋病月发病率预测,结果表明LM算法3-9-1 结构的BP 神经网络的MSE、MAE、MAPE 均小于ARIMA(2,1,2)(2,0,0)12模型,前者预测精度更高,与陈婷[9]的研究结果一致,证实在艾滋病发病率预测方面,BP 神经网络模型优于其他预测模型,预测结果说服力更强,可信度更高,因此LM算法3-9-1 结构的BP 神经网络模型的预测精度更好,更适合用于广西老年人艾滋病月发病率的预测;同时,其可以用来预测广西老年人艾滋病未来的发病趋势,利于卫生部门及时把握艾滋病的流行状况,制定应对策略,合理使用卫生资源。但本研究只考虑了时间与发病率之间的关系,并没有将影响广西老年人艾滋病发病率的具体因素作为变量纳入模型中,后期研究将进一步收集具体影响因素的数据资料放入模型中综合分析,优化模型,提高预测性能。
总之,本文构建的模型是基于历史报告数据所构建的,训练好的最优模型LM算法3-9-1 结构的BP 神经网络模型具有一定的时效性。若建模环境发生变化影响艾滋病疫情,模型的参数也会随着数据的改变而改变。此时,在相对稳定的大环境背景下,训练好的最优模型则不再适用,需要及时补充新的月发病率数据,重新训练建模拟合新模型,利用新模型做后续时间的预测,这样预测结果更具科学性和参考价值。
