基于电网拓扑优化的电压稳定预防控制方法

娄文静，王蕾，焦提操，刘洋，王聪，邓晓帆，孙建超

(山东理工大学电气与电子工程学院，山东 淄博255000)

0 引言

近年来，由于电力需求日益增长，系统的运行状态复杂多变，电力系统常运行于稳定极限附近[1 - 3]。若此时再发生故障或扰动，在事故和系统自身运行条件的双重作用下，电力系统的稳定运行状态极易遭到破坏，甚至引发电压崩溃，造成严重后果[4 - 5]。因此，通过采取有效的控制措施，增强电力系统的电压稳定性，尤其确保在各个预想事故状态下维持电压稳定，对于电力系统的安全稳定运行具有重要意义[6]。

通常增强电压稳定性的措施为切负荷[7]、无功补偿[8]和调节机组出力[9]等。文献[10]提出一种分群减载方法，该方法以电压降落对负荷的敏感度为指标，将电力系统的所有节点划分为不同群组，并为各组节点制定相应的负荷切除方案防止电压崩溃。文献[8]提出一种无功补偿选址方法，该方法通过对电压薄弱区域进行分析，综合考虑静止无功补偿器的容量等参数，以系统的综合电压增长为指标，确定最佳无功补偿点，提升系统的电压稳定性。文献[9]提出以法向量为指标调节发电机的输出功率，从而提高系统的输电能力，增强电力系统的安全性。

研究表明，网络拓扑结构的不合理是制约电网安全稳定运行的重要因素。文献[10]提出基于脆弱性评估，确定电网拓扑结构的加固方案，从而增强电网的韧性是电网研究工作的当务之急。文献[11]指出输电系统的可靠性与网架结构之间存在非同调现象，即元件的缺省反而会提升系统的可靠性。文献[12]提出采用输电线路开断和母线解列方法以增强系统的电压稳定性。文献[13]提出利用系统的开关操作可将网络结构调整到更合理的状态，基于新的拓扑结构采取其他控制方式可取得更好的调控效果。文献[14]提出输电线路投切在线拓扑优化方法以缓解电压越限，从而提高电力系统的安全性。

电力系统母线接线方式有单母线、双母线、双母线带旁路、二分之三等。以双母线接线为例，各条出线可连接到任何一条母线段，出线连接在不同的母线段，即称之为母线运行方式。母线运行方式优化作为优化电网拓扑结构的重要措施之一，已被应用于解决电压越限[15]、提高电压稳定性[16]和减小短路电流[17]等领域。文献[15]构建了模拟母线解列动作的模型，提出一种基于快速解耦潮流的方法以确定有效的母线解列和线路切换方案，从而消除由故障引起的线路过载和节点电压越限。文献[16]采用基于母线解列的拓扑优化方法以提升系统的负荷裕度，但该方法只研究基态电力系统的电压稳定性，并未考虑预想事故状态下的负荷裕度增强问题。

本文通过改变母线的运行方式，优化电力系统的网络拓扑结构，以提高电力系统的电压稳定性。由于电力系统母线运行方式众多，且计及大量预想事故，这些都增加了有效母线运行方案的求解难度。

为解决上述问题，本文提出一种计及预想事故的母线运行方式优化模型及求解方法。该方法基于阶段式的思想，先从全部母线运行方案中识别出使得预想事故满足运行约束的方案，进而从上述方案中求解可最大化基态系统负荷裕度的母线运行方案。该方法兼顾计算速度与精度要求，可降低预想事故集和众多母线运行方式带来的计算困难，适合在大规模电力系统中应用。

1 数学模型

本文用参数化的负荷裕度λ反映系统从稳定运行点到鞍结点分岔点(saddle-node bifurcation，SNB)的负荷变化，表征电力系统的静态电压稳定性[18]。

若当前电力系统的电网拓扑结构为N， 母线运行方式改变后基态电力系统的拓扑结构为Nb， 预想事故集为C， 可优化运行方式的母线集合为SB。 从能量管理系统和SCADA获取当前电力系统的状态、短期负荷预测数据、短期发电计划和维修计划，基态电力系统的负荷裕度可采用连续潮流方法计算得到，则计及预想事故的电压稳定预防控制问题的数学模型如下。

1.1 目标函数

本文所建立模型的目标函数为最大化基态电力系统的负荷裕度λb， 即

(1)

式中：λb为基态电力系统的电压稳定负荷裕度；bsk为母线k的某个运行方案，∀k∈SB。

1.2 约束条件

在本文所建立的模型中，约束条件包括以下几点。

1)母线运行方式改变后，基态电力系统和预想事故的潮流平衡方程分别表示为：

fNb(xb,λb)=0

(2)

fNci(xci,λci)=0， ∀ci∈C

(3)

式中：λci为预想事故ci的负荷裕度；Nci为预想事故ci发生后系统的网络拓扑结构。

2)预想事故的负荷裕度约束为：

λci(Nci(bsk))≥λth,c， ∀ci∈C

(4)

式中：λth,c为预想事故集的负荷裕度阈值，由运行人员根据需要设定。

3)母线运行方式改变后，基态系统和预想事故下的安全运行约束为：

Vi,min≤Vi,λ∈[0,1]≤Vi,max， ∀i∈M

(5)

|S(i,j)|λ∈[0,1]≤S(i,j),max， ∀(i,j)∈M

(6)

式中：Vi、Vi,max、Vi,min分别为节点i的电压幅值和上下限；S(i,j)、S(i,j),max分别为连接节点i和j的线路i-j上的功率及其限值；λ=0表示当前电力系统，λ=1表示预期电力系统；M为系统的全部节点集合。

最多允许改变运行方式的母线数量约束，该约束可表示为：

NE(Nb-N)≤m

(7)

式中：NE(·)映射为拓扑Nb和N的变化，即改变运行方式的母线数量；m为允许改变运行方式的母线数量限值，由运行人员根据需要指定。

本文所提问题是确保预想事故负荷裕度满足要求的情况下，求解最大化基态系统负荷裕度的母线运行方案。对于预想事故，本文主要关注其对系统负荷裕度的影响，研究所提方法对于事故后电力系统电压稳定性的增强效果。

2 母线运行方式分析及预想事故处理

2.1 母线运行方式的灵敏度分析

电力系统母线的运行方式多种多样，其运行方案总量庞大。对连接有n条支路(包括输电线路、并联电容和负荷支路)的母线k， ∀k∈SB， 其运行方案总数ss为[11]：

(8)

例如，一条连接6条支路的母线，共有25种运行方案；一条连接14支路的母线，则可产生的运行方案多达8 177个，这成为母线运行方式优化问题的求解难点之一。

为解决该问题，本文采用基于Ward的母线模型[16]，该模型适应性强，可简便模拟多种运行方案，且适于采用线性灵敏度方法对大量母线运行方案进行预筛选。依据该模型，任一母线运行方案可以等值为网状网络支路导纳的变化ΔY， 即：

(9)

为快速判别每个母线运行方案对电力系统静态电压稳定性影响，本文采用灵敏度方法[18]对全部运行方案进行预筛选。在连续潮流方法中，参数化的潮流方程表示为：

f(x,p,λ)=0

(10)

式中：x为状态变量；p为网状网络Nm的支路导纳；λ为负荷增长系数(即负荷裕度)。在SNB点对式(10)进行全微分计算，可得到：

(11)

(12)

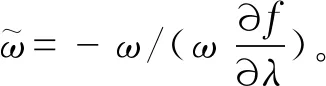
以网状网络Nm的支路i-j为例，若母线运行方式改变后支路i-j导纳变化量为Δpij， 则由此导致的负荷裕度变化量Δλij可表示为：

(13)

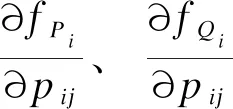
根据式(11)—(13)可计算Nm的全部支路导纳参数变化时的负荷裕度变化量。因此，任一方案bsk下负荷裕度的变化量可表示为：

(14)

式中nl为Nm的支路总数。

若Δλbsk≥0， 则表明按照方案bsk改变母线的运行方式后会增加系统的负荷裕度；反之，则减小系统的负荷裕度。由于灵敏度方法是一种线性化的估算方法，其计算速度快，因此可以在大量母线运行方案中进行预筛选，保留需要的方案。

2.2 预想事故的处理方法

在数学模型上，预想事故可以表示为整数变量，大规模电力系统的N-k(k=1,2,3…)预想事故数量众多，这使得整数变量的维数增加，成为本文所提问题的求解难点之二。对电力系统的预想事故逐个进行详细分析和计算是不必要且不切实际的[19]，若仅对最严重事故求解有效母线运行方案，则无法确保所求解的方案使全部预想事故满足约束条件。

为解决该问题，本文采用加权灵敏度方法对典型预想事故进行分析，保留加权灵敏度为正的母线运行方案。既可避免不必要的计算，又可兼顾对电压稳定性危害严重的预想事故。

3 母线运行方式优化计算方法

本文的母线运行方式优化问题考虑了众多预想事故，含有大量非线性的不等式约束，直接进行求解难度大且耗时多。因此，本文借鉴Benders算法[20]和文献[16]阶段式的思想，将其分解为两个子问题进行求解，求解流程如图1所示。

图1 母线运行方案求解方法流程图

两个子问题的数学模型分别为：

子问题1：预想事故有效母线运行方案求解，即式(3)—(6)对应的问题模型。

子问题2：基态系统母线运行方案求解。目标函数：式(1)；约束条件：式(2)和式(5)—(6)。

3.1 子问题1-预想事故有效母线运行方案求解

现代电力系统的在线电压稳定评估系统(VSA)中，预想事故扫描和分析是其中三大关键模块之一[5]。VSA的预想事故分析结果可以作为本文所提问题的输入数据，即根据VSA的分析结果，可以得到哪些预想事故的负荷裕度不满足阈值要求。将这些负荷裕度小于阈值的预想事故记为典型预想事故代表，用集合CRC表示。

首先应用连续潮流方法[21]对所有典型预想事故进行详细计算，可得到各典型预想事故的准确负荷裕度、SNB点节点电压幅值和雅可比矩阵零特征根对应的左特征向量，该子问题的求解方法如下。

步骤1(预筛选)：采用加权灵敏度方法快速筛选可提升典型预想事故负荷裕度的母线运行方案。根据式(13)—(14)，任一母线运行方案bsk下，典型预想事故cwi的负荷裕度变化量Δλcwi,bsk为：

(15)

式中：Δλcwi,ij为母线运行方式改变后支路i-j参数变化导致典型预想事故cwi负荷裕度的变化量。

因此，任一母线运行方案bsk对所有典型预想事故的裕度改善效果可用式(16)表示。

(16)

式中：λth,c为预想事故的负荷裕度阈值；CRC为负荷裕度低于阈值λth,c的预想事故的集合。

根据式(16)选择Δλc,bsk≥0的方案，生成备选母线运行方案集合CB。

CB={(bsk)|Δλc,bsk≥0}

(17)

步骤2(方案排序)：采用look-ahead裕度估算方法[22]计算集合CB的各方案下典型预想事故cwi的负荷裕度λcwi,bsk， 并采用如下指标对运行方案排序：

(18)

根据λc,bsk数值大小对备选母线运行方案进行排序，并将排序靠前的母线运行方案送入下一步进行详细计算。

步骤3(详细计算)：采用连续潮流方法按顺序逐个计算各母线运行方案下典型预想事故的准确负荷裕度，一直计算到第一个不满足式(4)的方案为止，并剔除不满足式(5)和(6)的运行方案。

至此，子问题1求解完毕，即该子问题的解能够使得所有典型预想事故的负荷裕度满足阈值要求。将求解结果送入子问题2进一步分析。

3.2 子问题2-基态系统母线运行方案求解

子问题1的解作为子问题2的备选方案，从中筛选出可提高基态电力系统负荷裕度的母线运行方案，具体方法如下。

步骤1(预筛选)：应用连续潮流方法对基态电力系统进行分析，得到基态系统的准确负荷裕度、SNB点各节点电压幅值和各支路功率、雅可比矩阵零特征根对应的左特征向量。然后应用线性灵敏度方法，对全部备选方案逐个计算负荷裕度变化量，并将正灵敏度(即Δλb,bsk≥0)的运行方案送入下一步进行计算。各备选母线运行方案下基态电力系统的负荷裕度变化量Δλb,bsk为：

(19)

式中：Δλb,ij为改变母线运行后，支路i-j参数变化导致的基态电力系统负荷裕度的变化量。

步骤2(方案排序)：采用look-ahead裕度估算方法评估各备选方案下基态系统的负荷裕度，并对运行方案排序，将排序后的方案送入下一步进行负荷裕度的准确计算。

步骤3(详细计算)：采用连续潮流法逐个计算各母线运行方案下基态系统的准确负荷裕度，并从解集合中剔除不满足式(5)和式(6)约束的方案。

3.3 校验

从解集合中逐个提取母线运行方案对预想事故集进行校验，对所有预想事故执行快速事故分析，检验该母线运行方式下所有预想事故的负荷裕度是否满足式(4)约束。若满足，则保留该方案；否则将该方案从解集合中剔除。重复执行快速事故分析，直到解集合中所有方案全部校验完毕。

若允许多条母线进行运行方式优化，即式(7)中m>1， 此时先识别单条母线优化运行方案，然后根据式(17)的筛选结果进行组合，生成多母线优化运行备选方案。由于识别出的所有单条母线运行方案能使预想事故的负荷裕度满足式(4)约束，则组合生成的方案也能使预想事故的负荷裕度满足阈值要求。因此，可直接转到子问题2，求解能够最大化基态系统负荷裕度的多条母线优化运行方案。

以上即为所提的母线运行方式优化求解方法，校验后的母线运行方式即为该方法所求解的有效母线运行方案。解集合中对应基态系统最大负荷裕度的方案即为“最佳解”。

4 算例仿真

本节采用IEEE 118节点系统和1 648节点系统对所提方法的有效性进行仿真分析，依次以单条母线运行方式优化、多条母线运行方式优化以及大规模电力系统为例对本文所提方法进行性能测试。

4.1 单条母线运行方式优化算例

118节点系统共有186条支路，69号节点为平衡节点，系统总负荷为4 242 MW和1 438 Mvar。该系统可优化运行的母线有21个，共生成292个母线运行方案。将系统的177个非辐射型线路的单条开断作为预想事故。本算例预想事故的负荷裕度阈值设置为λth,c=2.7。70—79号节点的8个负荷增长分别为98.98 MW、12.12 MW、6.06 MW、68.68 MW、47.47 MW、68.68 MW、61.61 MW和39.39 MW；32号、56号和80号节点发电机的有功功率输出分别为100.75 MW、161.20 MW和141.05 MW，用于平衡增长的负荷需求。采用本文所提的母线运行方式优化求解方法，结果如下：

典型预想事故分别为输电线路69- 70和76- 77开断，其负荷裕度为λc69-70=2.694 3，λc76-77=2.671 1。 子问题1的有效母线运行方案如表1所示，预想事故69- 70和76- 77的负荷裕度如表2所示。

表1 单条母线的优化运行方案

表2 母线运行方案下预想事故的负荷裕度

基态系统的负荷裕度λb=4.908 2，以表1的母线运行方案为子问题2的备选方案，基态系统的负荷裕度增长情况如表3所示。将189号和105号母线运行方案对预想事故集进行校验：按189号方案进行母线运行方式优化，由于λc74-75=2.444 1，λc76-118=1.921 2，不满足式(4)约束，因此，剔除189号运行方案；105号母线运行方案下，所有预想事故的负荷裕度均高于阈值λth,c， 如图2所示。105号母线运行方案即为所提方法求解的“最佳”方案，其局部电气接线图如图3所示。

表3 母线运行方案下基态系统的负荷裕度

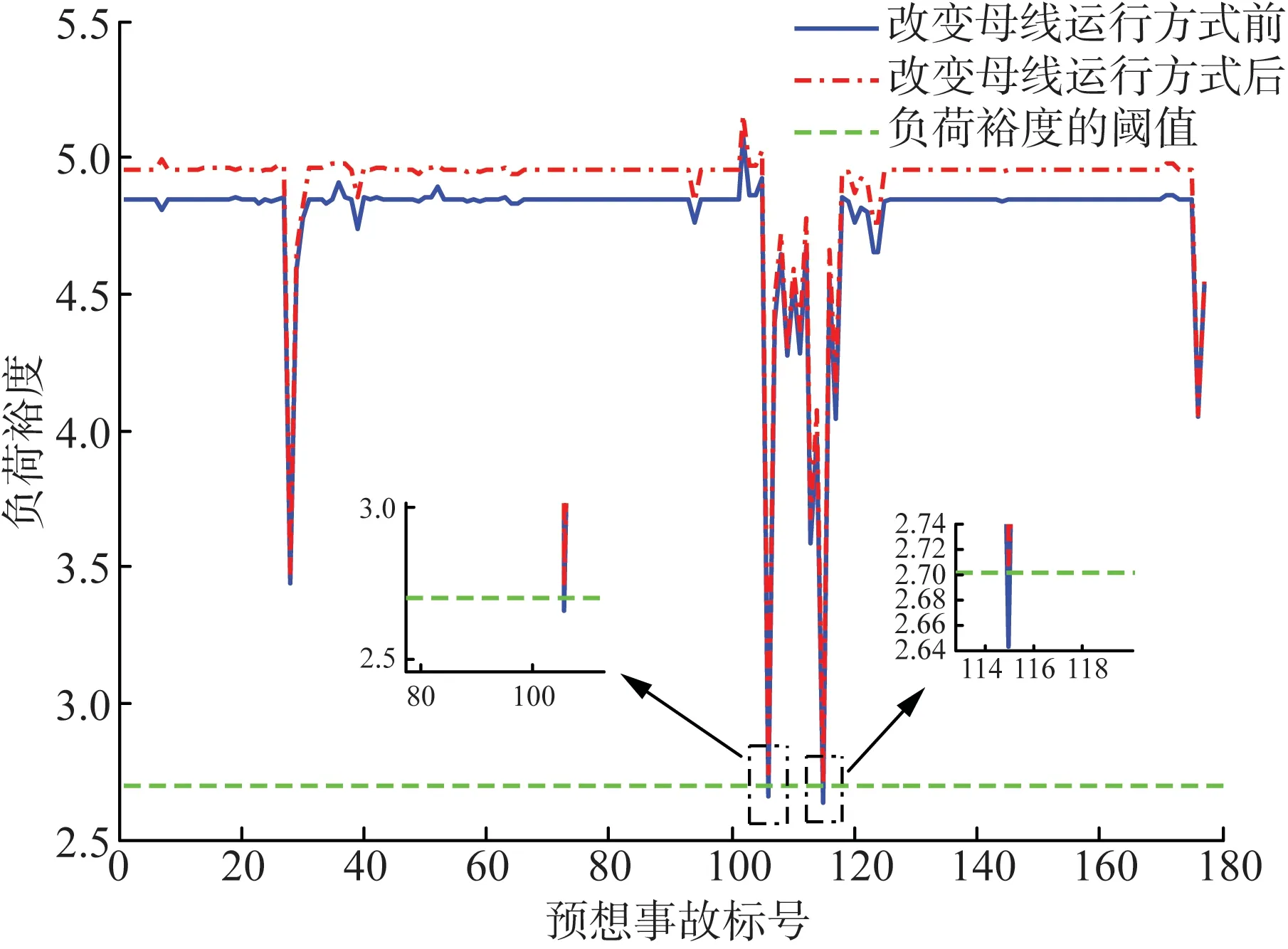
图2 母线运行方式改变前后所有预想事故的负荷裕度

图3 105号母线运行方案的局部电气接线图

4.2 多条母线运行方式优化算例

将118节点系统区域2的39个节点的负荷水平增长20%，1、4和31号节点的发电机输出的有功功率分别增加为151.41 MW、108.15 MW和173.04 MW，用于区域2增长的负荷需求。设置λth,c=3。

基态系统的负荷裕度λb=5.351 9，典型预想事故为线路30- 38开断，负荷裕度λc30-38=2.783 3。若m=2，即允许两条母线改变运行方式：先对单条母线的运行方案进行预筛选，保留正灵敏度的方案，再对保留的运行方案采用两两组合的方式生成备选母线运行方案，共3 854个。采用look-ahead裕度估算方法计算各备选母线运行方式下基态系统的负荷裕度并排序，对排序前10的组合方案，采用连续潮流方法计算预想事故30- 38和基态系统的负荷裕度，如表4所示，各母线运行方案对应的线路连接情况如表5所示。保留表4中前8组方案，并对预想事故集进行校验。有效母线运行方案为：52和21号、52和13号、90和21号、90和13号。其中52和21号方案组合对应基态系统最大负荷裕度，即为所求的“最佳解”。

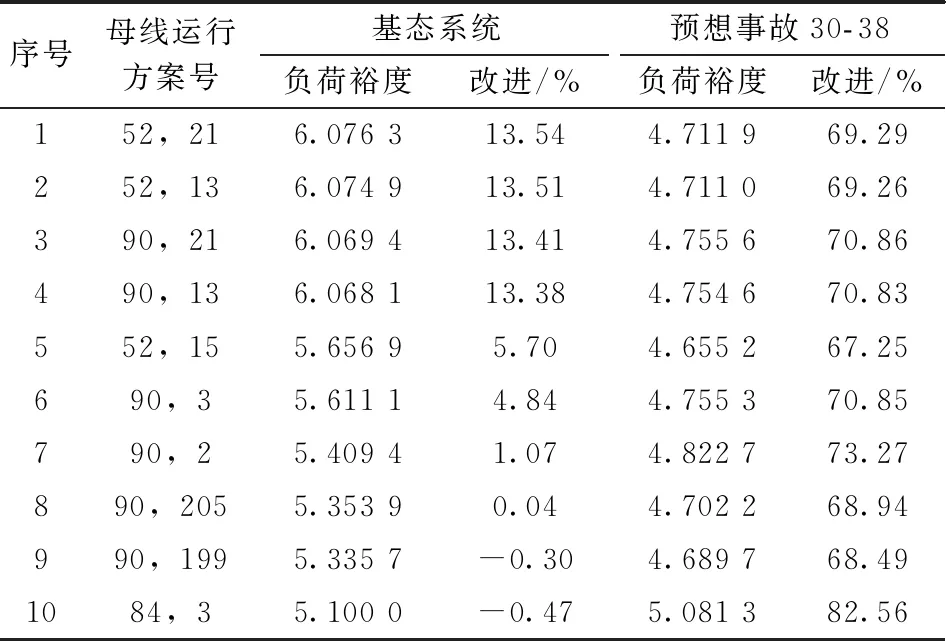
表4 两条母线运行方式优化后系统的负荷裕度

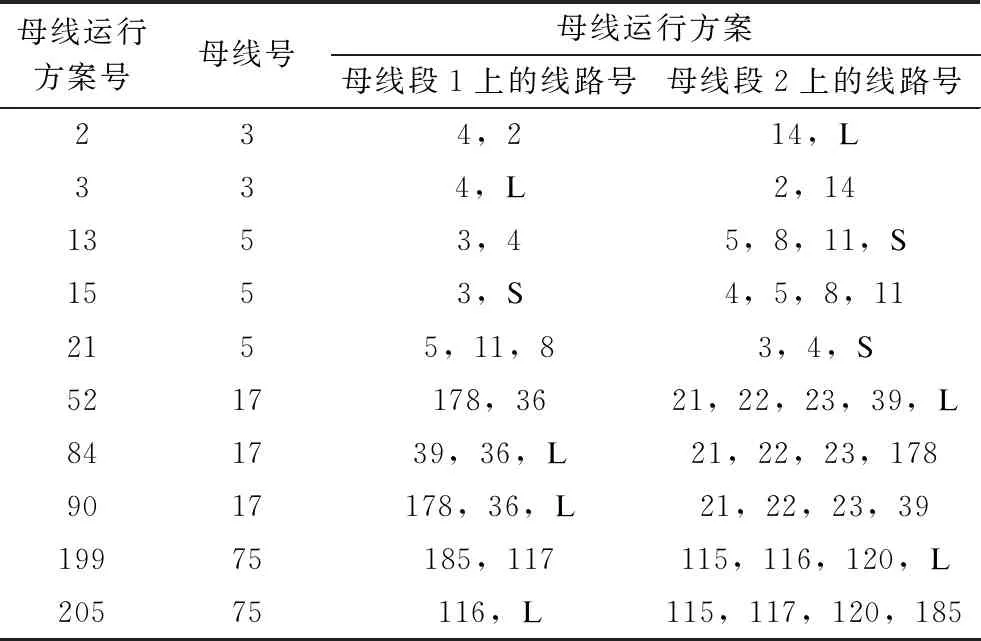
表5 母线运行方案对应的线路连接情况

按52、21号方案进行母线运行方式优化，基态系统和预想事故30- 38的P-V曲线如图4所示。

图4 运行方式改变前后基态系统和事故30- 38的P-V曲线

4.3 大规模电力系统算例

为进一步验证所提母线运行方式优化方法在大规模电力系统中的应用性能，本文采用IEEE 1 648节点系统展开测试。1 648节点系统共有792个可优化运行的母线，选择300个母线优化其运行方式，共生成7 972个运行方案。预想事故有927个，包括520个单条输电线路开断和407个两条输电线路开断事故。令λth,c=3.04。应用所提母线运行方案求解方法，结果如下。

基态电力系统的负荷裕度λb=8.742 2，典型预想事故为输电线路318- 372和282- 450同时开断，其负荷裕度为λc(318-372,282-450)=3.031 7。依次进行子问题1和子问题2的有效母线运行方案求解，结果如表6所示。表7为表6的各母线运行方式下基态电力系统和典型预想事故的负荷裕度。

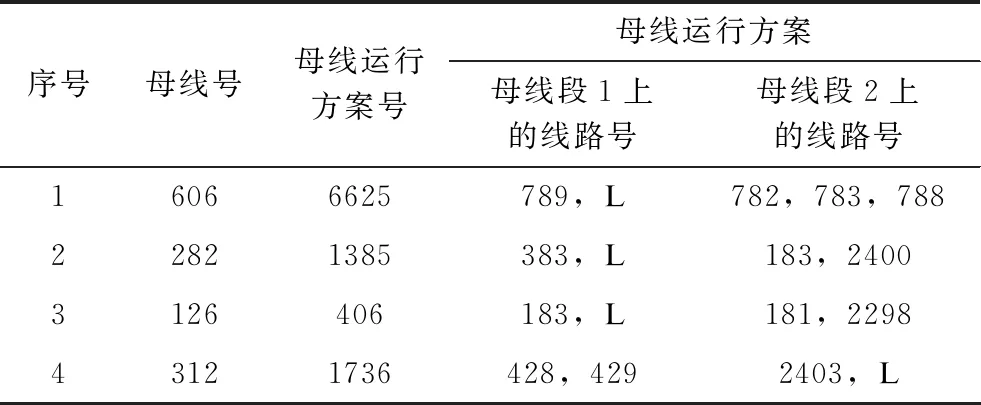
表6 1648节点系统的有效母线运行方案

表7 母线运行方案下系统的负荷裕度

将表6中的母线运行方案逐个对预想事故集进行校验，仅第6625号方案可使所有预想事故的负荷裕度满足式(4)约束，因此，该母线运行方案即为“最佳解”。

仿真结果表明，所提母线运行方式优化方法在大规模系统中具有良好的适应性，该方法可用于未来计及预想事故的电力系统电压稳定预防控制。

5 结论

本文提出了一种计及预想事故的母线运行方式优化模型，通过调整母线的运行方式，优化电网拓扑结构，以提升电力系统的负荷裕度，实现电压稳定的预防控制。基于分解的思想发展了计及预想事故的母线运行方式优化的求解方法。将原问题分解为两个子问题，分别采用“预筛选-方案排序-详细计算”的阶段式思想求解预想事故和基态系统的有效母线运行方案。求解的运行方案可在确保预想事故负荷裕度满足阈值要求的同时，提升了基态电力系统的静态电压稳定性。

在IEEE 118节点系统和1 648节点系统的仿真测试表明，所提方法能够有效地求解母线运行方案，优化网络拓扑结构，从而实现电压稳定预防控制。今后将进一步研究母线运行方式优化在电力系统日前电压稳定控制中的应用。