Experimental investigation on propagation characteristics of vortex beams in underwater turbulence with different salinity
2022-03-08LUTengfeiLIUYongxinWUZhijun
LU Teng-fei,LIU Yong-xin,WU Zhi-jun
(Fujian Provincial Key Laboratory of Light Propagation and Transformation, College of Information Science and Engineering, Huaqiao University, Xiamen 361021)
Abstract: It is very important to study the propagation characteristics of light beams in ocean turbulence. In order to get closer to the actual situation, we build a device which can control both the salinity and the intensity of underwater turbulence to study the propagation characteristics of vortex beams and a Gaussian beam in underwater turbulence. The results show that compared with the underwater turbulence without sea salt, the light spot will be more diffuse and the light intensity will be weaker in the underwater turbulence with sea salt. When the topological charge m is 2, the scintillation index of the vortex beam in the underwater turbulence with salinity of 4.35‰ is larger than that in the underwater turbulence with salinity of 2.42‰, no matter it is strong turbulence or weak turbulence. When the vortex beam with m=2 propagates to the same distance, the scintillation index increases with the increment of the salinity and the intensity of underwater turbulence. Under different salinity conditions, the radial scintillation index of the vortex beam with m=2 decreases firstly and then increases with the increase of the radial distance. In addition, we set up another experimental device which can transmit a longer distance. The scintillation index of the vortex beam with m=2 is much higher than that of the Gaussian beam in the underwater turbulence within 20 m propagation distance,and the scintillation indices of both the vortex beam with m=2 and the Gaussian beam increase with the increase of the propagation distance.
Key words: vortex beam; underwater turbulence; scintillation index; salinity; propagation
1 Introduction
Turbulence causes intensity fluctuations when the laser beam propagates in the random media,which is called scintillation[1-2]. The intensity fluctuation (scintillation) can reduces the signal-to-noise ratio and increases the bit error rate. Investigations of scintillation of laser beams in ocean turbulence become more and more important because of their wide applications in underwater optical communication and imaging[3-8]. In recent years, people have studied the scintillation index of laser beams in ocean transmission[9-19]. In Ref. [16], the scintillation of optical plane and spherical waves were investigated, and the results show that just like in the atmosphere, in underwater media the plane wave is more affected by turbulence as compared to the spherical wave. In Ref. [17], the aperture-averaged scintillations of plane and spherical waves were calculated. It was found that the adoption of the aperture-averaging technique in an underwater optical communication system can significantly extend its reliable communication distance. In Ref. [18], the on-axis scintillation index of a Phase-locked Partially Coherent Flat-Topped (PCFT) laser array beam in oceanic turbulence was studied, and the results show that in the sense of scintillation index reduction, using the PCFT array laser beams has a considerable benefit in comparison with the single PCFT or Gaussian laser beams and also Gaussian array beams. In Ref. [19], considering the pointing errors caused by the slight incline of underwater platform, the scintillation index of partially coherent beams propagating through weak oceanic turbulence were calculated. However, the above studies were all theoretical studies of scintillation index,and there were no experiments.
A beam with a spiral phase is called a vortex beam, and each photon of the vortex beam carries orbital angular momentum[20]. The research of the vortex beam is an important subject due to its potential applications in area such as optical micro manipulation, optical information encoding and transmission and other fields[21-24]. Based on the Huygens Fresnel principle, the spectral density, the spectral degree of coherence and the spectral degree of polarization of stochastic electromagnetic vortex beams in ocean turbulence were studied[25]. The propagation properties of the vortex beam in ocean turbulence were studied by using the spatial light modulator to show turbulence[26]. However, it is very difficult to do experiment in a real marine environment. Most of the relevant research results are obtained by computer numerical simulation. Targeting at above problem, we set up an experimental system containing underwater turbulence to investigate the scintillation index of the vortex beam in underwater turbulence, and research the influence of the different turbulence on the scintillation index[27]. In this paper, our main concern is the effects of salinity and propagation distance on the scintillation index and the intensity distribution of the vortex beams. We also establish another experimental equipment to make the beam propagate as far as 20 meters, which is longer than 12.6 meters in reference.
2 Experimental device of vortex beams passing through underwater turbulence
The experimental system configuration for generating a vortex beam and measuring its intensity fluctuation in underwater turbulence is shown in Fig. 1. The laser with wavelength of 532 nm is utilized as a light source. The beam is propagating through a telescope system consisting of two lenses(L1andL2), whose focal lengths are 5 cm and 15 cm, respectively. The expanded beam is converted into a vortex beam by passing through a Spiral Phase Plate (SPP). The topological charge of the vortex beam is determined by the structure of the SPP. The generated the vortex beam then transmits through an underwater turbulence simulation device(called Simulator), where the intensity of underwater turbulence is controlled by the flow rate of circulating pump water. Figure 2 shows the practical photo of the experimental device, where Fig. 2 (a) is weak turbulence and Fig. 2 (b) is strong turbulence.Since the length of Simulator is 1.8 meters, in order to enable the beam transmit over the longer distance, the reflectors M1and M2are used. A detector for measuring the scintillation index is employed,which contains an opto-electron detector with a round role of 5 mm in diameter. The optical signal is converted electrical signal by opto-electron detector, and then the Scintillator is used to collect the electrical signal to measure the scintillation index.

Fig. 1 Schematic diagram of vortex beams propagating in underwater turbulence. L1, L2, thin lenses; SPP,spiral phase plate; M1, M2, reflectors

Fig. 2 The practical photos of the experimental device. (a)Weak turbulence; (b) strong turbulence

Fig. 3 The scintillation of the vortex beam with m=2 transmitted to 3.6 meters in weak underwater turbulence with the SA =2.42 ‰
Figure 3 shows the scintillation index of the vortex beam withm=2 transmitted to 3.6 m in weak underwater turbulence with salinity of 2.42 ‰, the horizontal coordinate is time, and the vertical coordinate is the scintillation index measured in real time. The sampling time is set to 1ms during the experiment, and the sampling frequency is set to 1000 times.
In this study, the scintillation index is measured by a detector with a round role of 5 mm in diameter, which means that the scintillation refers to area scintillation index. Recently, the aperture averaged scintillation has been proposed to study the scintillation in a certain region, which is defined as[28]
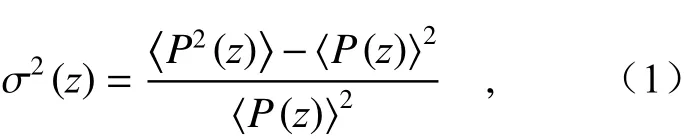
where

3 Experimental results and analysis
Now we discuss the intensities of the vortex beam withm=2 propagating through different underwater turbulences in the experiment. The spot is taken by the beam analyzer. In order to avoid overexposure during shooting, the attenuator is used to attenuate the light intensity, resulting in the loss of a little detail of the spot. Figure 4 (Color online)shows the intensity patterns of the vortex beam withm=2 propagating in both the weak and strong underwater turbulences with salinity of 0. As shown in Fig.4, the light intensity is obviously weakened with the increasing transmission distance in both the weak and strong underwater turbulence. While, the disturbance of the beam in the strong turbulence is significantly higher than that of the beam in the weak turbulence. Figure 5 (Color online) shows the intensity patterns of the vortex beam withm=2 propagating in both the weak and strong underwater turbulence with the salinity of 2.42‰. By comparing the experimental results in Fig. 4 and Fig. 5, it can be found that in the presence of sea salt, the light spots are more diffuse and the light intensity is weaker.

Fig. 4 The intensity patterns of the vortex beam with m=2 propagating in both the weak and strong underwater turbulences with salinity of 0. (a) z=3.6 m, weak turbulence; (b) z=3.6 m, strong turbulence; (c) z=5.4 m, weak turbulence;(d) z=5.4 m, strong turbulence
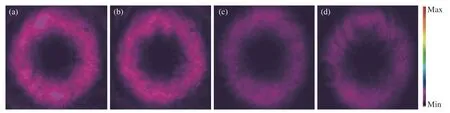
Fig. 5 The intensity patterns of the vortex beam with m=2 propagating in both the weak and strong underwater turbulences with the salinity of 2.42 ‰. (a) z=3.6 m, weak turbulence; (b) z=3.6 m, strong turbulence; (c) z=5.4 m, weak turbulence;(d) z=5.4 m, strong turbulence
Figure 6 presents the scintillation index of the vortex beam withm=2 varying with propagation distance in the turbulence with different salinities. It can be found from Fig. 6 that the scintillation index of the vortex beam in the underwater with salinity of 4.35‰ is bigger than that of in the underwater with salinity of 2.42‰, no matter it is strong turbulence or weak turbulence. This is because that increasing the salinity of underwater is approximately equivalent to increasing the turbulence of underwater. Figure 7 illustrates the effect of the salinity on scintillation index of the vortex beam withm=2 at 3.6 m propagation distance. We can also find that the greater the salinity of seawater is, the larger the scintillation index is in both weak and strong turbulence, and the scintillation index of the vortex beam withm=2 in the strong turbulence is higher than that of the vortex beam withm=2 in the weak turbulence.

Fig. 6 Scintillation index of the vortex beam with m=2 varying with propagation distance in the water turbulence with different salinities in (a) weak turbulence and (b) strong turbulence

Fig. 7 The effect of salinity on scintillation index of the vortex beam with m=2 at 3.6 m propagation distance in (a) weak turbulence and (b) strong turbulence
Figure 8 shows the scintillation index varying with the radial distance of the transverse plane in the underwater with different salinities. It can be seen from the Fig. 8, the radial scintillation index of the vortex beam withm=2 decreases firstly and then increases with increasing the radial distance. In addition, the center of the vortex beam has a dark core surrounded by a bright ring. The intensity increases at first, and then decreases. Thus, the change of scintillation index with radial distance is opposite to that of intensity with radial distance.
As the current experimental device needs mirror reflections for a long-distance transmission, the light intensity becomes weak and cannot transmit further. So, we build another experimental device to directly transmit the beam over a longer distance without mirror reflection, as shown in Figure 9.Figure 10 presents the scintillation indices of the vortex beam and a Gaussian beam varying with propagation distance. In Fig. 10, we can find that within the 20 m propagation distance, the scintillation index of the Gaussian beam is much smaller than that of the vortex beam withm=2, and the scintillation indices of both the vortex beam and the Gaussian beam increase with the increment of the propagation distance. This can be in part understood by their intensity distribution. The vortex beam does not travel long enough, so the vortex beam does not evolve into Gaussian distribution.The light intensity in the center of the vortex beam is much weaker than that of the Gaussian beam, the same turbulence may produce greater fluctuation for the vortex beam, so the scintillation index of the vortex beam withm=2 is much larger than that of the Gaussian beam. The evolution of scintillation indices of the vortex beam and a Gaussian beam is similar with the results obtained in Ref. [27], but for a longer distance.

Fig. 8 Scintillation index of the vortex beam with m=2 at 3.6 m propagation distance in (a) weak turbulence and (b) strong turbulence

Fig. 9 Experimental device of direct long-distance transmission

Fig. 10 Scintillation indices of the vortex beam and the Gaussian beam varying with propagation distance(no turbulence)
4 Conclusion
In conclusion, we have experimentally investigated the intensity fluctuations when vortex beam and Gaussian beam is propagating in underwater turbulence. The light intensity is obviously weakened with the increasing transmission distance in both the weak and strong underwater turbulence with salinity of 0. It can be found that in the presence of sea salt, the light spots are more diffuse and the light intensity is weaker. It is shown that the scintillation indices of both the vortex beam and the Gaussian beam increase with the increment of the propagation distance. It also can be found that the scintillation index of the vortex beam in the underwater with salinity of 4.35‰ is bigger than that of the vortex beam in the underwater with salinity of 2.42‰, no matter it is strong turbulence or weak turbulence. At 3.6 m, the radial scintillation index of the vortex beam withm=2 decreases firstly and then increases in underwater turbulence. In order to make the beam travel a longer distance, we set up another experimental device. Within the 20 m propagation distance, the scintillation index of the vortex beam withm=2 is much larger than that of the Gaussian beam,and the scintillation indices of both the vortex beam withm=2 and the Gaussian beam increase with the increment of the propagation distance. The research results obtained by our experiments have important value in exploring the application of vortex beams in oceanic turbulence.
杂志排行
中国光学的其它文章
- 《中国光学》约稿信
- 院士访谈
- Enhancing the fluorescence emission by flexible metal-dielectric-metal structures
- 《发光学报》
——EI核心期刊(物理学类;无线电电子学、电信技术类) - Illustrating the Helmholtz-Kohlrausch effect of quantum dots enhanced LCD through a comparative study
- Fabrication of an ultra-narrow band-pass filter with 60 pm bandwidth in green light band
