Research on Deep Learning Algorithm for Lie Group Features
2022-03-08YANGMengduoLIFanzhang
YANG Mengduo,LI Fanzhang
(1.School of Information Technology,Suzhou Institute of Trade and Commerce,Suzhou,215009,China;2.Provincial Key Laboratory for Computer Information Processing Technology,Soochow University,Suzhou,215006,China;3.School of Computer Science and Technology,Soochow University,Suzhou,215006,China)
Abstract:Since complex data in the real world can often be represented as Lie group structures,this paper designs a deep network ar-chitecture with Lie group features as input,so as to make use of the powerful feature representation ability of deep learning for pat-tern recognition and other tasks.In the process of constructing Lie group deep neural network,in order to ensure that Lie group fea-tures can be restricted to the structure of differential manifold during optimization,a deep learning algorithm suitable for Lie group features was introduced.In the process of feature learning,the algorithm can not only ensure that the information of data manifold structure is not lost,but also limit the assumption space of parameter optimization.The deep learning algorithm based on Lie group features is applied to CIFAR-BW and MNIST data sets,and the Lie group features of the spoke models are designed for static imag-es.The experimental results show that the proposed algorithm can converge to a more ideal result in fewer iterations.
Key words:Lie group features;deep learning;spoke model;image classification;representation learning
1 Introduction
Since Lie groups are differential manifolds that can be transformed continuously,Lie group features are often used to represent complex data in the real world[1].For example,in the study of machine learn-ing algorithms,a large part of training and test sam-ples are matrix forms besides the common vector forms.In many existing applications,a large number of matrices constitute Lie groups,such as the general affine transformation group of two-dimensional imag-es.The left and right Singular vector matrices ob-tained after Singular Value Decomposition(SVD)of any matrix constitute a general linear group.And the covariance matrix is also a Lie group after adding the corresponding group operation.Deep learning can au-tomatically learn important feature information of da-ta and has a strong ability of nonlinear modeling[2-5].Therefore,deep learning quickly shows great advan-tages of feature learning[6-10].Since there are a large amount of data to form the Lie group structure in real-ity,and deep learning is a very good tool for feature learning,it is natural to combine them.In reality,one possible scenario is that the data represented by Lie group structure require deep learning algorithm to car-ry out tasks such as pattern recognition.In order to ensure that Lie group features can be limited to the structure of differential manifolds when optimized by deep neural networks,this paper studies the deep learning algorithm of Lie group features.The algo-rithm can not only learn the features without losing the information of the data manifold structure,but al-so greatly limit the hypothesis space of parameter op-timization.The main contributions of this paper are:(1)The Lie group structure features of the spoke mod-el were designed for the static image;(2)The optimi-zation process of the deep neural network is limited to the differential manifold structure and the Lie group structure is not destroyed;(3)The data with Lie group characteristics are combined with deep learning to converge to a relatively ideal result in a few itera-tions.
2 Related Work
Literatures[11]and[12]studied the transforma-tion matrix Lie group and its corresponding Lie alge-bra representation in the visual tracking problem,and used Lie group in image affine transformation to mod-el the transformation of the focus target in video and image.Although the image pixel representation of the tracked and detected objects is different in differ-ent image frames,the transformations between them are mainly affine transformation,so the Lie group method can represent the relationship between them in essence,so as to achieve better tracking effect and detection rate.Using similar ideas,literature[13]studied visual invariance using Lie group affine trans-formation combined with EM algorithm under the framework of weak perspective affine transformation of two-dimensional images.Compared with tradition-al methods,Lie group method does not lose too much image information.In literature[14],Lie group Lie algebra method is successfully applied to represent transformation process,so as to learn dynamic visual flow and reveal the internal relationship between Lie group Lie algebra and linear dynamic process.At the same time,regional covariance matrices are directly processed as samples.By analyzing their differential geometry structure,the distance between samples is calculated for target recognition and detection[15]and pedestrian detection in video[16],both of which surpass the algorithms in similar top journals on the same problem.M-Rep model[17-18]is a Lie group represen-tation of 3D objects,which can represent a three-di-mensional object of arbitrary shaped by a group of Lie groups.The automobile point cloud[10]in the two-dimensional image space can also be conveniently constructed into Lie group samples,the Principal Geo-desic Analysis(PGA)[17]is used to design the classifi-er,and the classification effect is significantly better than that of the linear method[19-20].It can be seen that Lie group method has good advantages in image trans-formation modeling and feature representation.
3 Spoke Model
The point cloud representation of the target ob-ject is extracted from the image,and the spoke model of the target object is modeled on the basis of the point cloud representation.Point cloud representation of the target object,generally speaking,is to select a number of points on the target object to represent the target object.Because the extracted points are ob-tained from the still image,the points are located in the two-dimensional plane R2.
The coordinate system is established for the stat-ic image.A two-dimensional vector can be formed by connecting the origin to any point in the point cloud.This two-dimensional vector can be visualized as a Spoke Si.Each spoke is determined by two parame-ters,the length of the spokeriand the amount of two-dimensional rotation between the spoke and the prin-cipal axis ni.Finally,the spoke model of the target object can be obtained by connecting all points in the point cloud to the center point.The point cloud repre-sentation of handwritten number 0 and the spoke mod-el of handwritten number 0 in MNIST dataset are shown in Fig.1(a)and Fig.1(b),respectively.

Fig.1 (a)A point cloud representation of the handwritten digit 0;(b)a spoke model of the handwritten digit 0
Assuming that fixed k points are selected on the image of each handwritten digital instance,then the whole constituted X by the k spokes can be used to represent a handwritten digital instance,i.e.
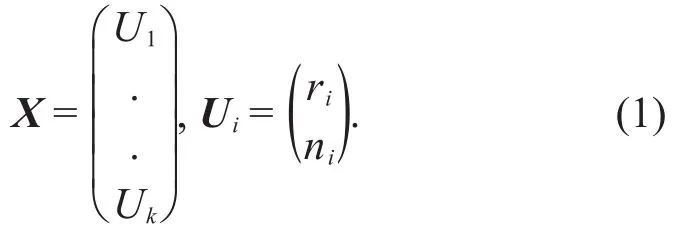
Now given a handwritten number spoke model X,define the transformation T such that X transforms to Y under T,i.e.,Y=T(X).In matrix form we can write Y=TX,where
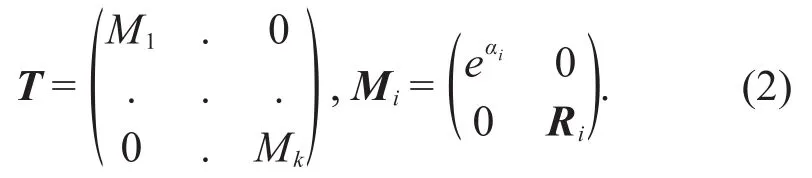
In the above representation,eαirepresents the scale applied to the radius ri,and Rirepresents the two-dimensional rotation applied to the normal vec-tor.By transforming T,different instances of hand-written numbers can be represented as transforma-tions of X.Therefore the transformation matrix T can be used as a feature to describe handwritten numbers.
In the application of classification,the classifica-tion standard can be defined as:if the transformation matrices T1and T2obtained by transforming the refer-ence handwritten number X to two other handwritten number instances Y1and Y2,are similar,then the two handwritten number instances are considered to be-long to the same kind of number category;On the oth-er hand,if the transformation matrices are very differ-ent,it is likely that the two handwritten number in-stances do not belong to the same number category.
4 Lie Group and Lie Group Network
4.1 Lie Groups

In a network of Lie groups,each input is a mem-ber of the Lie group.The spoke transformation ma-trix T is the Cartesian product of the transformation matrix Miapplied to each spoke.Each Miis a Lie group of R×SO(2),because the Cartesian product of the elements of a Lie group is still a Lie group,and therefore T constitutes a Lie group.The Lie algebra elements of T can be obtained by logarithming Mione by one.
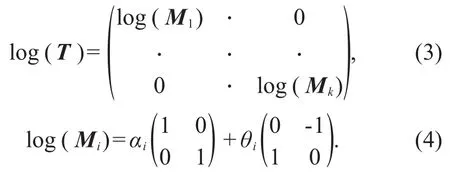
Eq.(4)represents a spoke Siin terms of scaling and two-dimensional rotation on the generator ma-trix.αiand θiare the generator coefficients for scal-ing and rotation of spoke Si,respectively.
4.2 Single Hidden Layer Feed Forward Net-work
We know that back-propagation algorithms can be used to learn the weights of multi-layer networks,which use gradient descent to try to minimize the square of the error between the network output and the target value.Given the training set D={(x1,y1),(x2,y2),…,(xm,ym)},xi∈ Rd,yi∈ Rl,that is,each input sample is described by the d-dimensional feature,and the output is the l-dimensional real value vector.Fig.2 shows a feedforward network structure with a single hidden layer.The input layer of the net-work has d input neurons,the hidden layer has q hid-den layer neurons,and the output layer has l output neurons.The weight of connection between the ithneuron in the input layer and the hthneuron in the hid-den layer is vih,and the weight of connection between the hthneuron in the hidden layer and the jthneuron in the output layer is whj.
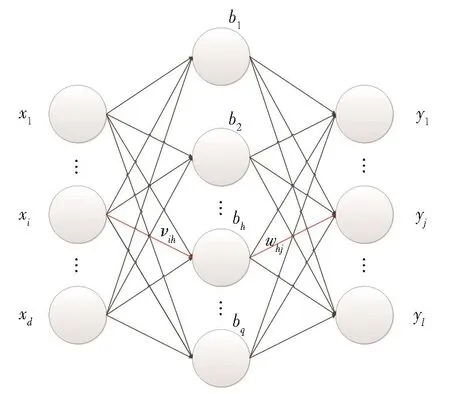
Fig.2 Structure of a single hidden layer feedforward network and its variable symbol
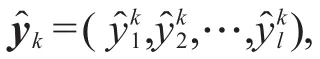

Among them,

where sigm(⋅)stands for sigmoid activation function.
And the input received by the hthneuron in the hidden layer is

The input received by the jthneuron in the output layer is

where bhis the output of the hthneuron in the hidden layer.
Let the input vector be X=[x1…xi…xd]T,and the connection weight matrix between the input layer and the hidden layer is

Then,the input received by the hthneuron in the hidden layer is

The input received by the hidden layer as a whole can be written as α=VTX.
Let the hidden layer vector be B=[b1…bh…bq]T,and the connection weight matrix between the hidden layer and the output layer is

Thus,the input received by the j-th neuron in the output layer is
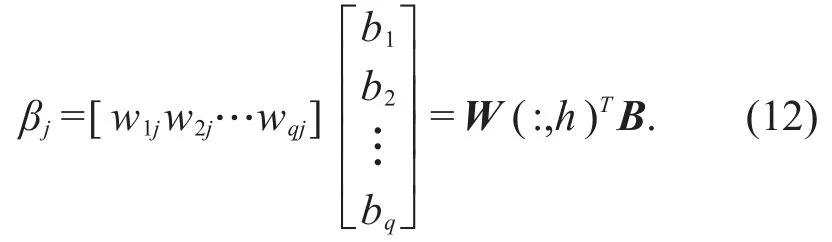
Input received by the output layer as a whole can be written as β=WTB.
For simplicity,the thresholds of the hidden layer and output layer neurons are ignored,and both the hidden layer and output layer neurons use sigmoid as the activation function.Let the output vector be Y=[y1…yj…yl]T,then
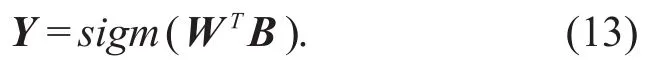
where W is a weight matrix of order q×l,and B is a column vector of order q×1.
4.3 Lie Group Networks
Without regard to supervised or unsupervised learning,the adaptive adjustment of a neural network can often be viewed as an optimization problem:a nu-merical optimization process that allows the tunable parameters of the network to be changed using an ob-jective equation describing the task performed on the network.This means that the learning process of a neural network can be viewed as a search or nonlinear programming problem in a parameter space.Howev-er,this parameter space is quite large.Any prior knowledge of the search for the optimal solution,if fully utilized,can greatly narrow the search.The prio-ri knowledge mentioned here includes the optimal so-lution of the neural network for the current task,as well as some performance indicators.
Lie group networks attempt to embed a priori knowledge of the geometric characteristics of net-work parameters in the network learning process.The rules embedded in the prior knowledge can be re-garded as limiting the network parameter space to a Lie group structure from the perspective of the geo-metric structure of the network parameter space.When updating the network parameters,the con-straints on the spatial geometry of the network param-eters should be considered.This means that the Lie group network also needs to design a learning rule compatible with this constraint.Next,this section de-scribes the mathematical modeling of a single layer Lie group network.
Firstly,the geometric structure of the parameter space of the Lie group network is constrained to re-strict it on Stiefel manifolds,that is,the weight matrix W between the input of layer i and the output of layer i+1is restricted as follows:
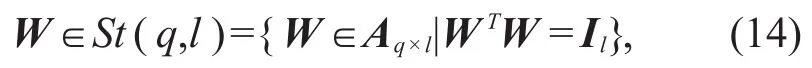
where,St(q,l)is Stiefel manifold,Aq×lrepresents the matrix of order q×l,and Ilis the identity matrix of or-derl.
In the multi-layer network of deep learning algo-rithm,if the traditional back propagation algorithm is used to return the output layer error,gradient diffu-sion will be caused.Therefore,the weight training can be carried out by using the method of layer by lay-er training of the auto-encoder and the way of pre-training the network weight.
Thus,the learning problem of an autoencode-based single-layer Lie group network becomes an op-timization problem as shown in the following func-tion.

where B̂=(WT)-1sigm-1(Y),Y=sigm(WTB).
Thus,for a sample set of capacity m,the objec-tive function of the optimization problem can be ex-pressed as


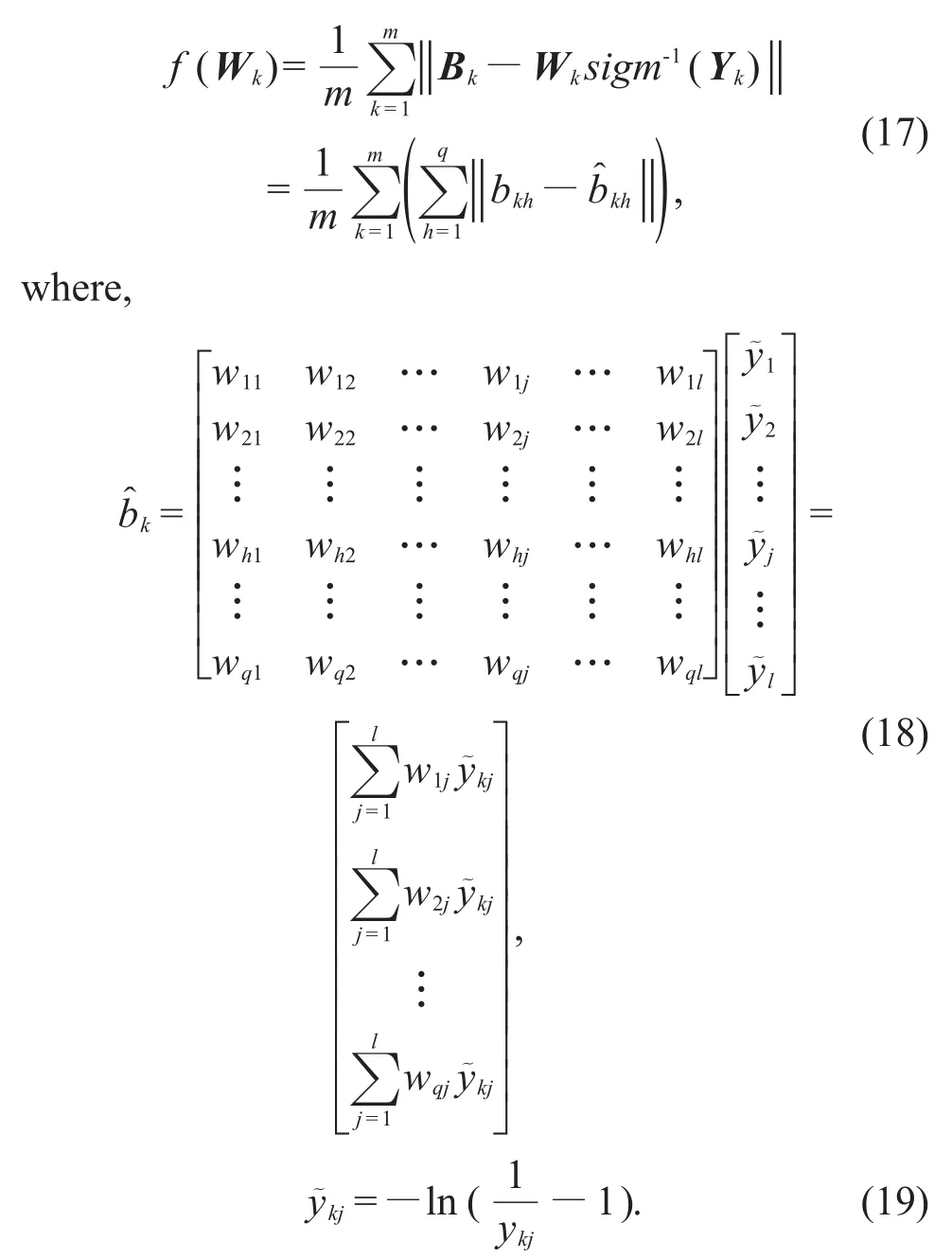
So we can expand f(Wk)to get

5 Training Process
With the mathematical modeling of a single lay-er Lie group network,the process of building a deep network becomes the process of stacking multiple lay-ers and training the whole network.
In terms of presentation,deep learning hopes to build a deep structure by stacking single-layer train-ing modules on top of each other.Compared with tra-ditional machine learning methods such as support vector machine,Boosting,and logistic regression,deep learning can achieve infinite approximation of complex functions through a deep nonlinear network.This solves the problem that shallow learning has lim-ited ability to represent complex functions in the case of finite number of samples and calculation units.In short,the benefit of deep learning's multilevel repre-sentation is the ability to represent very complex func-tions with fewer parameters.
The deep representation adopted by deep learn-ing can bring two very significant advantages:on the one hand,the deep structure can gradually learn more abstract features,because with the increase of the number of layers,the concepts with a lower degree of abstraction can help build more abstract concepts;On the other hand,depth structure can provide a more ex-pressive distributed representation,so that different combinations of features can correspond to different representations of input,and can better describe the intrinsic information of rich data.
6 Experiments
In order to further verify the advantages of the deep learning algorithm of Lie group features for fea-ture description,we compare the classification perfor-mance on the CIFAR-BW dataset.CIFAR-BW is the grayscale version of the CIFAR-10 dataset.CIFAR-10 contains 60 000 images in 32×32 color,including 50 000 training images and 10 000 test images.The en-tire dataset is divided into 10 classes,including planes,cars,birds,cats,deer,dogs,foxes,horses,boats and tanks,each of which contains 6 000 imag-es.On this data set,we compare the classification performance of the algorithm proposed in this paper with some deep learning algorithms based on auto-en-coders.After supervised fine-tuning,the algorithm's classification performance under different iteration times is shown in Table 1.The algorithms for com-parison include basic stack auto-encoder SAE,de-formed auto-encoder SAE-W with weight attenuation constraint,noise reduction auto-encoder DAE-G with Gaussian noise training,and noise reduction auto-en-coder DAE-B with binary noise shielding.In the above SAE algorithm and its deformation algorithm,both encoders and decoders adopt sigmoid activation function and optimize the objective function by using stochastic gradient descent method in the training pro-cess.Firstly,two hidden layers with 200 nodes are used to construct the neural network.Each deep learning algorithm adopts the same network struc-ture.

Table 1 Comparison among classification error rate of different algorithms
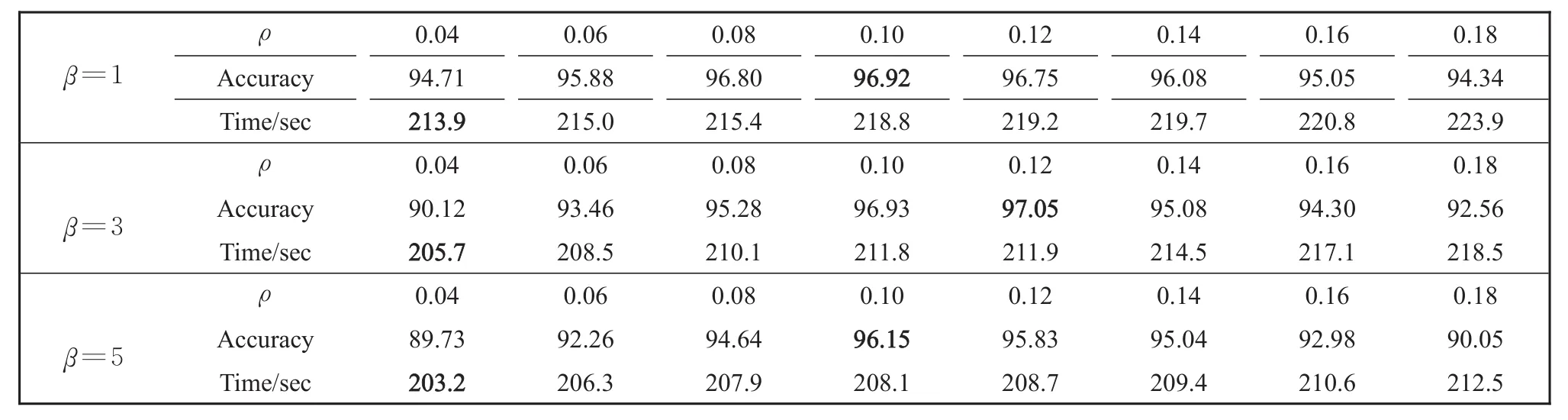
Table 2 Comparisons of sparsity and recognition rates of Lie group models
From the perspective of accuracy,in the experi-ment comparing the classification performance of two groups,when the number of iterations is enough,the classification effect of Lie group impression deep learning is lower,but the accuracy difference is not much.From the view of the corresponding iteration times,the new algorithm of constrained network pa-rameter space is more suitable for the application of low accuracy but fast classification.
In addition to the comparison of classification performance with other algorithms,we also analyze the influence of Lie group manifold size and sparse degree on prediction accuracy and time of Lie group impression deep learning algorithm.We present the experimental results of MNIST using traditional stacked auto-encoders and deep learning models based on Lie group impressions.In the algorithm,the sparsity degree is determined by the sparsity penalty weight b and sparsity parameter ρ.The effects of the two parameters on algorithm performance are shown in Table 2.
7 Conclusion
We test the performance of a deep learning algo-rithm for Lie group features to generalize from a small number of samples,that is,to limit the weight parameters of the network connection on the matrix Lie group structure.In particular,because constraints limit the parameter range of weights,deep learning of Lie group features can provide a smaller weight search space than traditional deep neural network al-gorithm models.On the premise that the computa-tional complexity is acceptable,the ideal accuracy can be obtained by finding the appropriate size of manifolds.The parameter space can be limited within an appropriate range by selecting the appropriate num-ber of hidden nodes,and the described geometric structure can be used to describe the Lie group charac-teristics of the object,making it easier to find a rela-tively optimal solution in the iterative updating pro-cess under this premise.
