学科间衔接与思政元素在“电路分析基础”课程中的应用研究<br/>—以“叠加定理”为例

学科间衔接与思政元素在“电路分析基础”课程中的应用研究
—以“叠加定理”为例

2022-03-07崔海峰周国军赵冬梅

智库时代 2022年3期

崔海峰周国军赵冬梅

（海军大连舰艇学院）

引言

“电路分析基础”是系统学习电学类知识的首门课程，其主要从电路模型出发，研究电路的基本理论和分析方法，以及工程技术中典型电路的特点和规律，是后续学习“模拟电路”和“数字电路”重要的理论基础。例如在“模拟电路”中分析共射放大电路的直流通路时，就用到了基尔霍夫电压定律列写KVL方程，从而求出静态工作点；再如在“数字电路”中分析555构成的单稳态触发器的暂稳态持续时间时，需要应用一阶动态电路的三要素法进行求解。

在学习“电路分析基础”课程时，如果学生没有课程间衔接的思维，很容易出现片面理解的问题，在后续学习“模拟电路”和“数字电路”时也会因为“电路分析基础”环节薄弱从而导致学习困难。所以在学习“电路分析基础”时，适当地将“模拟电路”和“数字电路”中的知识点渗透给学生，有助于提高学生的学习兴趣、降低学习难度，从而提高学习效果[1]。

高校的立身之本在于立德树人。习近平总书记指出：建设政治素质过硬、业务能力精湛、育人水平高超的高素质教师队伍是大学建设的基础性工作。强调要把思想政治工作贯穿教育教学全过程，实现全员育人、全程育人、全方位育人，努力开创我国高等教育事业发展的新局面[2]。

“电路分析”是电学类课程的重要基础，是学生接触相关专业课程的第一步。因此，在“电路分析基础”中融入课程思政，以知识为载体实现社会主义核心价值观的教育，是完成“立德树人”伟大目标的重要环节。

“叠加定理”是“电路分析基础”课程中的主要定理之一，它的内容是：在线性电路中，任意一条支路上的电流（或电压）都等于电路中的每一个独立源单独作用在该支路产生的电流（或电压）的代数和[3]。定理的内容简单明了，很容易理解，却在电路分析中起着非常重要的作用，在分析多个独立源共同作用的线性电路时非常具有优势，同时也广泛地应用于动态电路和正弦稳态电路的分析。笔者的思路是先以新闻热点作为导入，以“数字电路”中的典型电路作为引例提出问题。在讲授“叠加定理”的内容之后，应用定理解决问题。进一步讨论定理是否可以应用于非线性电路时，借助EWB虚拟仿真验证得出结论，并渗透“模拟电路”中求解非线性电路的重要方法。在讲解“叠加定理”的思想时，融入思政元素。

一、与“数字电路”结合：时事导入，引例贯穿

2021年10月16日0时23分，神舟十三号载人飞船发射成功，顺利将三位宇航员送入太空。火箭在发射和飞行时，需要实时采集飞行的姿态和速度等信息，控制箭体的运行轨迹，确保将飞船精确地送入预定的轨道。这里以最新的新闻时事迅速抓住学生的思维，可以在很大程度上激发学生的学习兴趣。

从信号控制的角度看，火箭采集到的信号和调整的相关信号都是连续的模拟信号，而核心控制器接收和发送的是抗干扰能力强、传输质量高的数字信号，这两种信号需要进行实时精确的转换。模数转换器和数模转换器就是联系模拟信号和数字信号的枢纽。

引例图即为一个简化的数模转换器的原理电路图。（注：实际的数模转换器中电压源大小都为U，而作为本节课的引例，为了在讲授“叠加定理”时对每个电压源的作用加以区分，这里标为U1、U2、U3。）之后简述数模转换器的原理：其中三个电压源的支路中都含有一个电子开关，开关的断开与闭合由输入的数字信号是0还是1来决定。数字信号为0时开关断开，为1时开关闭合。当输入的数字信号不同时，三个开关状态不同，输出电流I会随之改变，从而可以将数字信号转换成模拟信号。这里通过引例渗透了“数字电路”中数模转换器的原理，也让学生对模拟信号和数字信号有了初步的认识，为之后“数字电路”的学习做了非常好的铺垫。如图1所示。

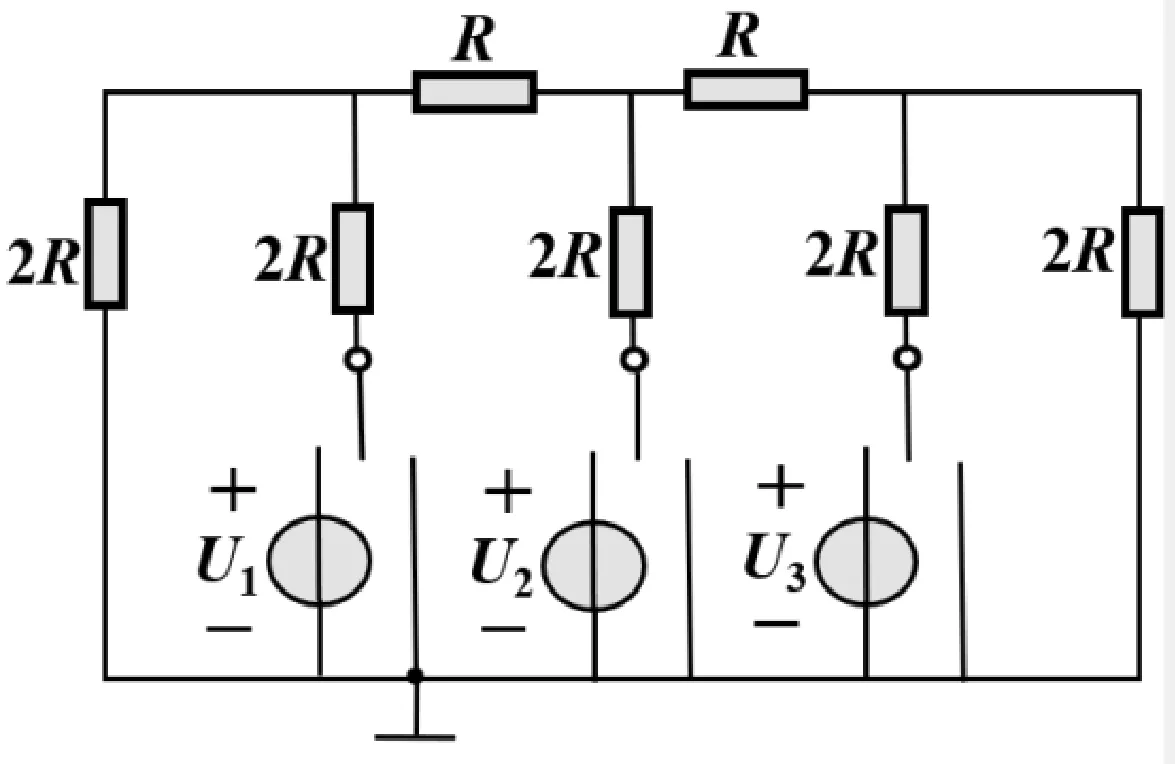
图1 引例的电路图

接着让学生利用之前课程中学习过的支路电流法，求解当输入的数字信号为111时，右侧2R电阻的支路电流I。此电路中共有7条电流未知的支路，需求解7个KCL和KVL方程组成的方程组。通过上述分析过程学生会发现，用支路电流法求解这种含有较多个独立源的复杂电路，方程数量较多、求解计算量较大。但是通过最后的计算结果可以看出，电流I是由三项相加而成的，每项都和电路中的三个电源U1、U2、U3成正比。此时引导学生联想，是不是可以分别考虑每个电源单独作用在电路上，对电流I的贡献呢？同时提出对于这种含有多个独立源共同作用的电路，如何能够避免求解方程组从而简化分析和计算的问题，从而顺理成章地引出了“叠加定理”的内容，使得定理的讲授水到渠成，同时激发了学生的主动思考。

在讲授完定理的内容之后，应用定理求解引例电路。原电路之所以求解复杂，就是因为其中含有多个独立源和电阻，并且它们交织在一起。而学习了“叠加定理”之后，学生就会发现，定理可以将电路分成多个单电源的电路，这样除电源所在支路外，电路的其他部分变成了简单的电阻串并联结构，很容易进行直接化简，通过口算就可以得出结果。并且在分析过程中可以发现，相应支路的数字信号为1时，总电流I中才包含该支路的电量，从而实现数字信号转换为模拟信号的功能。这样回扣数模转换器的原理，用引例作为线索贯穿了定理的讲授，可以有效激发学生的思考，使学生茅塞顿开、醍醐灌顶，也使定理的讲授和求解的过程成为了一个有机的整体。

二、与“模拟电路”结合：虚拟仿真，拓展思维

为了加深学生对于“叠加定理”的理解，笔者在EWB虚拟仿真软件中搭建了一个含有二极管的电路，来讨论定理是否适用于非线性电路。

从仿真结果上看，两电源单独在4Ω电阻上的电流之和不再等于它们共同作用时的电流，即不再满足“叠加定理”。此时引导学生主动思考，原因就在于引入了一个特殊的元件—二极管。我们知道，二极管和电阻最大的区别是电阻的阻值不会随其两端电压的变化而变化，伏安特性曲线是一条直线，它是线性器件；而二极管的阻值却会随其两端电压的变化而变化，伏安特性曲线是一条曲线，它是非线性器件。因为在应用“叠加定理”分解电路前后，二极管两端的电压会发生变化，导致其阻值改变，从而电路参数随之改变。引导学生得出结论：“叠加定理”不适用于非线性器件组成的非线性电路，只适用于线性电路[4]。如图2所示。

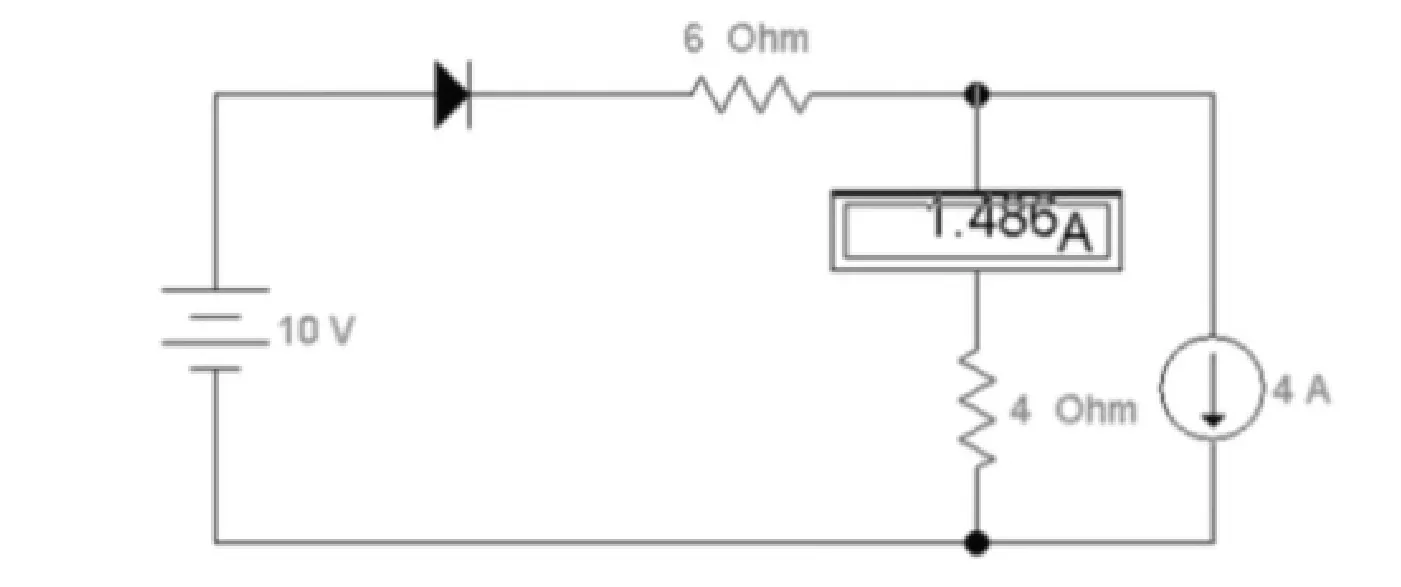
图2（a） EWB虚拟仿真的电路图-原图

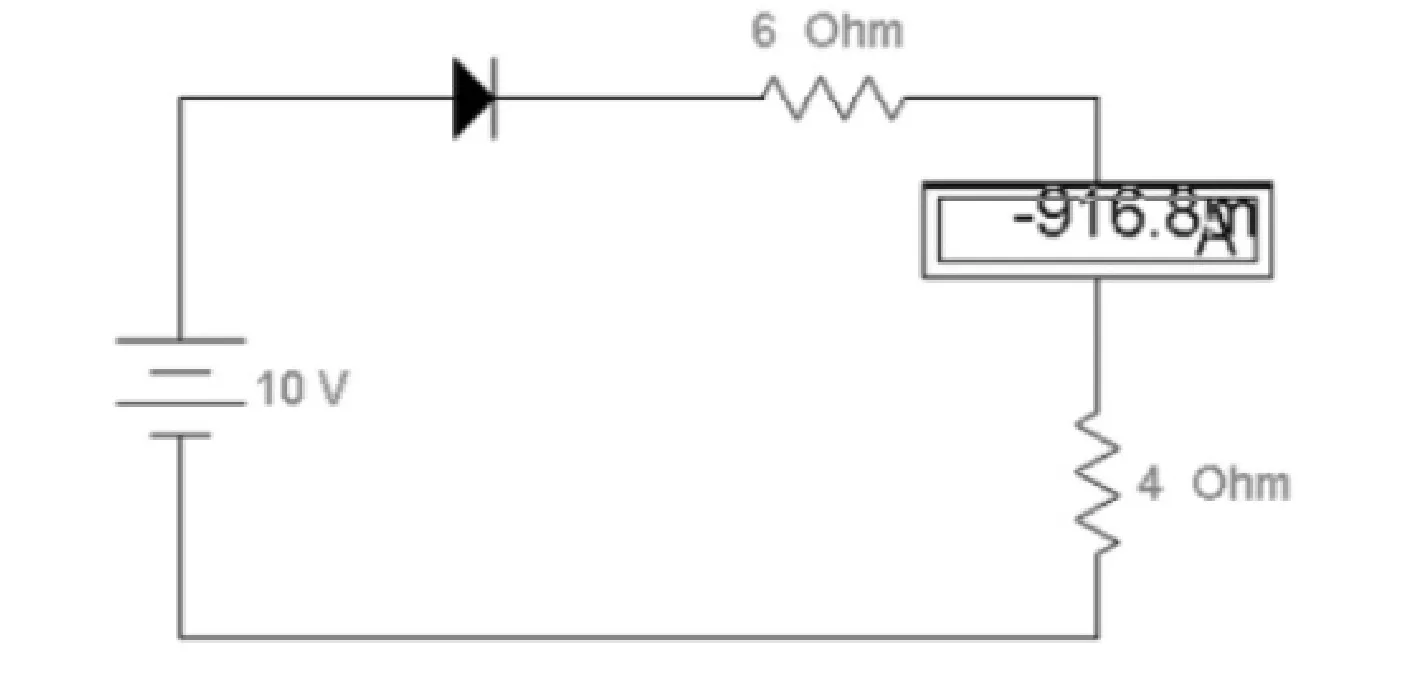
图2（b）电压源单独作用分解图

图2（c）电流源单独作用分解图

为了进一步提升学员的认知水平，提出问题：对于非线性电路，“叠加定理”真的就毫无作为了吗？此时引导学生头脑风暴或以小组的形式进行讨论，由老师进行点评，之后给出定理在非线性电路中的应用场景。

一种场景，是在分析仿真电路中二极管两端的电压和电流时，可以将电路的非线性和线性部分分开考虑，这两部分具有相同的电压U和电流I。对于电路的线性部分，可以采用叠加定理等线性分析方法，最后等效成一个电压源和电阻串联的最简形式，其伏安特性曲线是一条直线；对于非线性部分的二极管，其伏安特性曲线是一条过原点的曲线。因为二极管端口的U和I既要符合线性部分，又要符合非线性部分，所以U-I平面上两条特性曲线的交点即为所求支路上的U和I。这就是“模拟电路”中分析非线性电路时常用的一种方法—图解分析法。如图3所示。

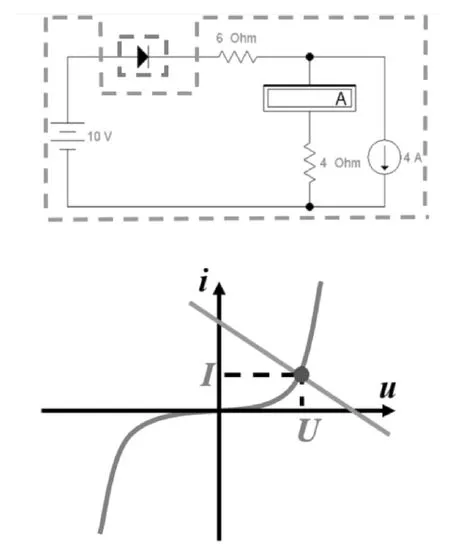
图3 图解分析法分期二极管冠电压及电流

另一种场景，就是将非线性器件线性化，那么整个电路就变成了线性电路，我们就可以利用叠加定理进行分析。比如当二极管两端承受正向电压时，它可以用一根导线来代替；当两端承受反向电压时，可以用开路来代替，这就是二极管的理想模型。这两种情况下电路都变成了线性电路，进而我们就可以应用“叠加定理”等线性分析方法进行分析，这就是模拟电路中另一种分析非线性电路的方法—模型分析法。

从以上两种场景中学生可以体会到，“叠加定理”虽然产生于线性电路，但是在非线性电路中仍然大有用处。同时，笔者通过对“叠加定理”在非线性电路中应用的讨论，将“模拟电路”的分析思维和重要方法渗透给学生，润物细无声，既拓展了学生的思维，这为后续“模拟电路”的学习打下了坚实的基础。

三、融入思政元素：军味特色，升华主题

针对笔者所在院校的性质，如何将专业知识与课堂思政巧妙地融合，并体现军校的特色，成为了培养新时代军人的重要环节。对于“叠加定理”，笔者从辩证唯物主义世界观和方法论的角度切入，形象地类比毛泽东军事思想并进行了深入剖析。

通过对数模转换器电路的分析可知，当含有多个电源时，电路的复杂程度提高了，而学生的分析能力是有限的。在电路的复杂程度与学生的分析能力构成的矛盾中，复杂程度是矛盾的主要方面。

如同敌我双方在战场上，敌方有装备精良的30个团的兵力，而我方只有装备落后的10个团的兵力，双方力量悬殊，此时敌方是矛盾的主要方面。但我方应用的是毛泽东军事思想中机动灵活的游击战、运动战的战略战术，将敌人的一个或几个团调动出来，使其脱离其大部队，造成相反的、悬殊的力量对比，形成我方的巨大优势。此时我方成为了矛盾的主要方面，从而可以集中优势兵力将敌方一举歼之。

“叠加定理”就是这种灵活的战略战术，它帮助我们将复杂的电路分解为一个个简单的电路，此时我们的分析能力成为了优势，从而可以将简单的电路逐个击破。这种“分而治之”的思想不仅适用于直流电路，也广泛地应用于“电路分析基础中”后续学习的动态电路和正弦稳态电流电路中。

这里将马克思主义哲学与毛泽东思想进行了巧妙地融合，使学生学有所思、学有所悟，从理性和感性两方面立体的感受“叠加”思想的精妙之处，即虽然是在“电路分析基础”课程中所学，【作者简介】崔海峰（1989-），男，满族，硕士研究生，助教，研究方向为电工电子教学。但在其他课程的学习过程中，甚至人生中遇到困境之时，都可以采用“叠加”的思想将复杂、困难的工作进行分解，逐个解决。由此，提高了学生的辩证思维与思想高度，同时体现了习近平总书记强调的“立德树人、为战育人”的新时代思政教学的方针。