基于高斯噪声的HLSM稳健性多变点检验

朱小雪，施三支，银炳皓

（长春理工大学 数学与统计学院，长春 130022）

变点检验是时间序列分析的重要组成部分，时间序列数据的均值、方差或模型系数在未知的时刻突然发生了改变，可能标志着数据生成的重大变化，因此变点检验必不可少。变点检验问题第一次被提出可追溯到20世纪50年代［1］，现在已经被拓展应用于股票、生物、基因数据、网络流量分析、交通等领域，并且已经有着广泛的研究，变点检验方面已经有着大量文献，如Kim（2019）［2］、Cheng（2015）［3］、Liu（2020）［4］、Kurt（2018）［5］、王红玉（2018）［6］等。

对于变点检验，在早期工业质量控制上，Page（1954）［1］基于 CUSUM 检验了观测值的累积和超过阈值的位置。Scott（1974）［7］提出一种二进制分割（Binary Segmentation）算法用于近似多变点检验，用成本函数最小化将序列分割成互不相交的段。Killick（2012）［8］提出 PELT算法，将成本函数最小化来求解变点的方法加以拓展，对于潜在的变点进行了修剪。Maidstone（2018）［9］提出一种FPOP算法，通过成本函数最小化求解序列中多变点的精确值。

稳健性是变点检验的一个重要方面，近几年也有文章研究变点的稳健性。如Fearnhead（2019）［10］提出一个动态算法能最优分割序列，选择对异常点不敏感的损失函数，解决当序列中存在异常时变点被高估的问题。Dehling（2019）［11］基于两样本的Hodges-Lehmann检验证明当噪声是重尾分布的情况下有着好的检验效果。许多变点检验算法，在高斯噪声异常值存在的情况下检验均值变化缺乏鲁棒性。基于似然比检验的方法（Yau，2015）［12］、基于惩罚似然的方法（Killick，2012）［8］，这类方法对重尾噪声表现出一定的鲁棒性，但在实际应用中，检验出的变点数会高于实际变点。

本文提出了一种基于高斯噪声Hodges-Lehmann Scan方法（HLSM），可在全局序列中推断多变点的问题，通过窗口滑动简化成在局部窗口中检验单变点的问题。通过数值模拟实验与PELT和BS方法进行了比较，结果表明HLSM方法与带有准则的HLSM方法具有较高的稳健性。

1 HLSM方法

1.1 模型与基本假设

假设观测序列{Xt}t=1,...,n={X1，…，Xn}，将自回归（AR）过程分为m+1段。对于j=1，…，m，第j个变点τj表示自回归过程中第j段突变到第j+1段的位置，假设τ0=0和τm+1=n，并且τ0<τ1< … <τm<τm+1。序列的第j段表示为：

其中，μt是每段序列中未知的常数；Yt,j是均值为零的自回归过程，并满足：

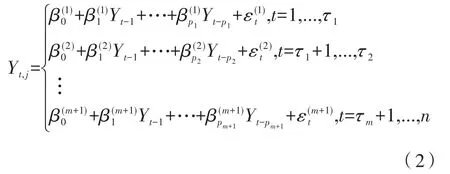
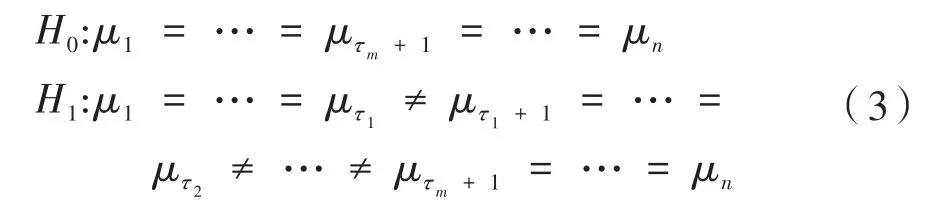
其中，i=1,…,m，假设每一段都是独立的时间序列，将多个假设检验问题视为检验两个相邻段 (Xτi-1+1,Xτi-1+2,…,Xτi)和 (Xτi+1,Xτi+2,…,Xτi+1)的μi是否相等。本文采用了窗口滑动方法结合Hodges-Lehmann检验来解决假设检验问题（4），称为Hodges-Lehmann Scan方法。

1.2 Hodges-Lehmann Scan

在1.1节中，未定义每段阶数pi取值，假设每段的阶数最大值为整数pmax。通过Hodges-Lehmann检验的扫描统计量估计出序列中潜在的变点。假设窗口半径h=h(n)取决于样本量n。定义在t处的窗口和窗口中的观测值分别为：

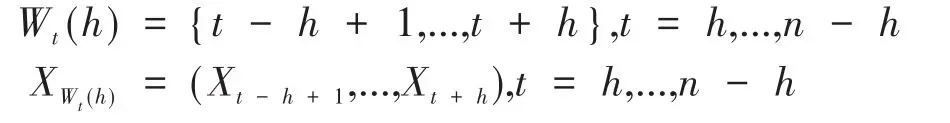
为了在窗口中检验变点，选择Dehling（2019）［11］中采用的Hodges-Lehmann检验统计量：

通过Mn(t)检验统计量，在窗口中能够得到一组Hodges-Lehmann检验统计量的值(Mn(h)，Mn(h+1)，…，Mn(n-h))。若t处是变点，则Mn(t)值是在局部窗口中的最大值。因此通过HLSM得出一组潜在的变点值，定义如下：

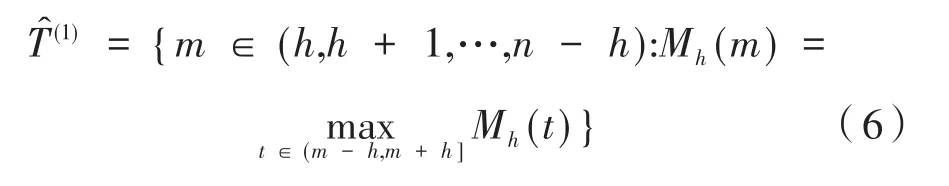
1.3 模型选择

时间序列中常用最小化准则函数估计多变点，在这里选择 Davis（2006）［13］提出的最小描述长度（minimum description length；MDL）准则。

给定一组样本z=(z1,…,zn)，定义准似然函数为：

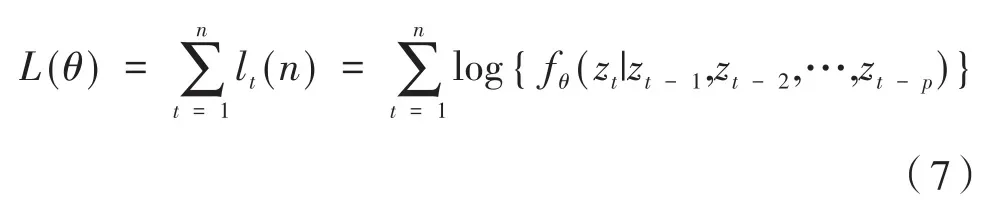
给出最小描述长度的定义为：

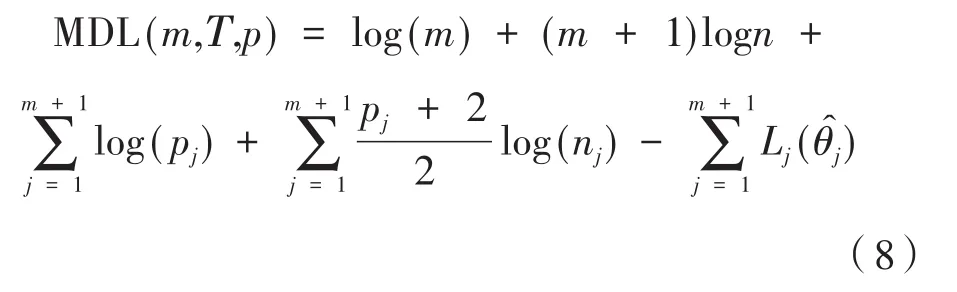
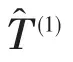
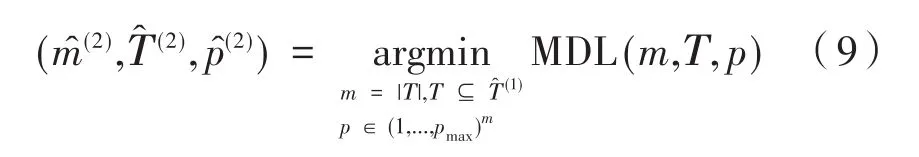
1.4 HLSM算法步骤

在算法1中给出了HLSM算法的具体步骤：

步骤（一）：输入一系列观测值：X1,…,Xn，Xi∈R，设置窗口半径为h=dlog(n)2；

2 模拟实验

在本节中，比较了PELT、BS（Binary Segmentation）和HLSM的两种方法，即HLSM和加最小化描述长度准则（MDL）的HLSM，模拟数据由式（1）生成，给出了在同方差与异方差的高斯噪声下，无异常值和有异常值等不同场景下参数变化的实验结果。

2.1 模拟基础设置

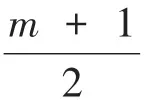
为了评估变点估计的性能，根据Killick（2012）［8］中提出的真阳率（True positive rate，TPR）和假阳率（False positive rate，FPR）评估每个方法检验变点的能力。对于每个数值实验，定义：

其中，l表示算法检测到的总变点数；l1表示l中检测正确的变点数，真实的变点是τi∈Τ，若方法检验到的变点τ̂i是距离真实变点τi的10个点的范围内，同样认为检验到的该变点为真实点。

2.2 模拟实验

对于均值结构的变化，设置漂移的均值μi=Ui(a,a+0.5)，服从独立同分布的均匀分布，设置a=1.5是低信号水平，a=2.5是高信号水平。

图1给出了低信号场景下（a=1.5），不同算法和不同样本量下估计的真阳率和假阳率（TPR和FPR）。图1中的场景A，从左图的TPR折线图中看出，除了样本量在500时，PELT较大以外，其他样本量都是HLSM方法更好，结合右图FPR折线图，当样本量为500时，PELT的FPR是最大的，能判断PELT算法有较大的TPR是因为高估了变点值。在场景B中，对于额外的方差变化，从TPR折线图中看出，HLSM也很稳健，另外两种经典的算法PELT和BS，在FPR折线图显示出，不同样本量之下，FPR都较高，由此得知这两种方法都会高估变点。对于加了异常值的场景C下，HLSM方法的TPR在各样本量下，保持最高，能够精确估计变点位置，此外应用了模型准则的HLSM方法的FPR在场景A、B、C下都为最优。综合看，HLSM的两种方法有着不错的变点检验效果，两种方法的侧重优点不同，其中HLSM方法有较高的真阳率（TPR），而加了模型准则的HLSM方法则有着更小的假阳率（FPR）。但是相比于PELT和BS方法而言，本文提出的两种方法在真阳率有着较好检验效果的同时，能够保持更小的FPR。

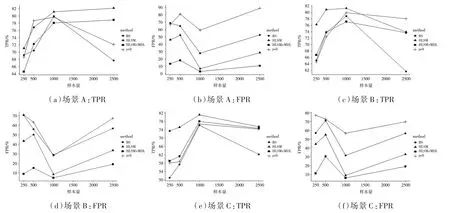
图1 低信号水平下：真阳率与假阳率折线图

图2给出的是在高水平信号（a=2.5）下，样本量为250的场景C中，四种方法实验模拟得出的一次结果，其中左边虚线是真实变点的位置，右边虚线是方法估计出的变点位置。从图中观测出，PELT和BS方法误判异常值的位置为变点，导致高估变点的数目。但HLSM的两种方法在有着异常值的场景下，忽略异常值的干扰，不会高估变点，对比PELT和BS方法有着较高的稳健性。

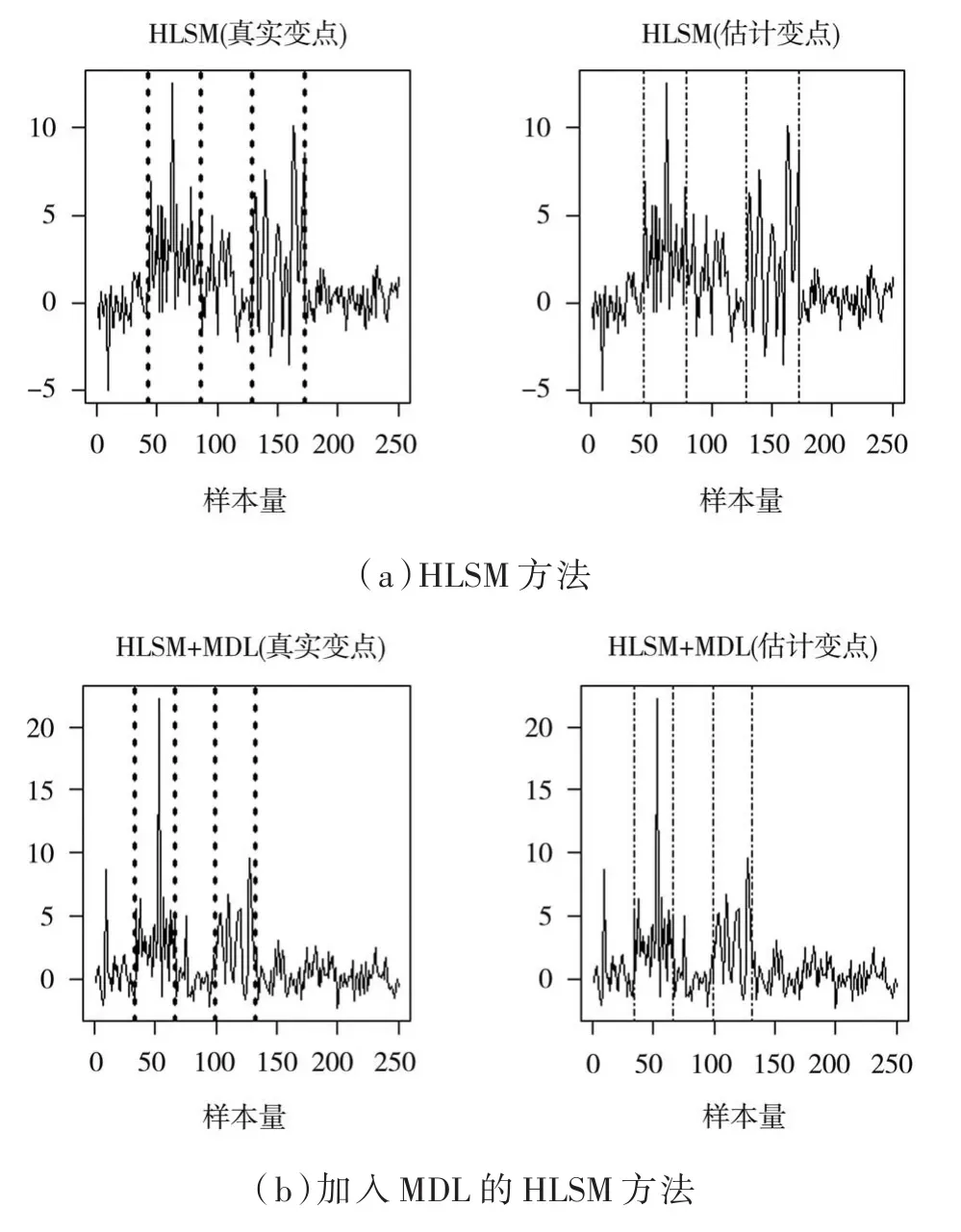
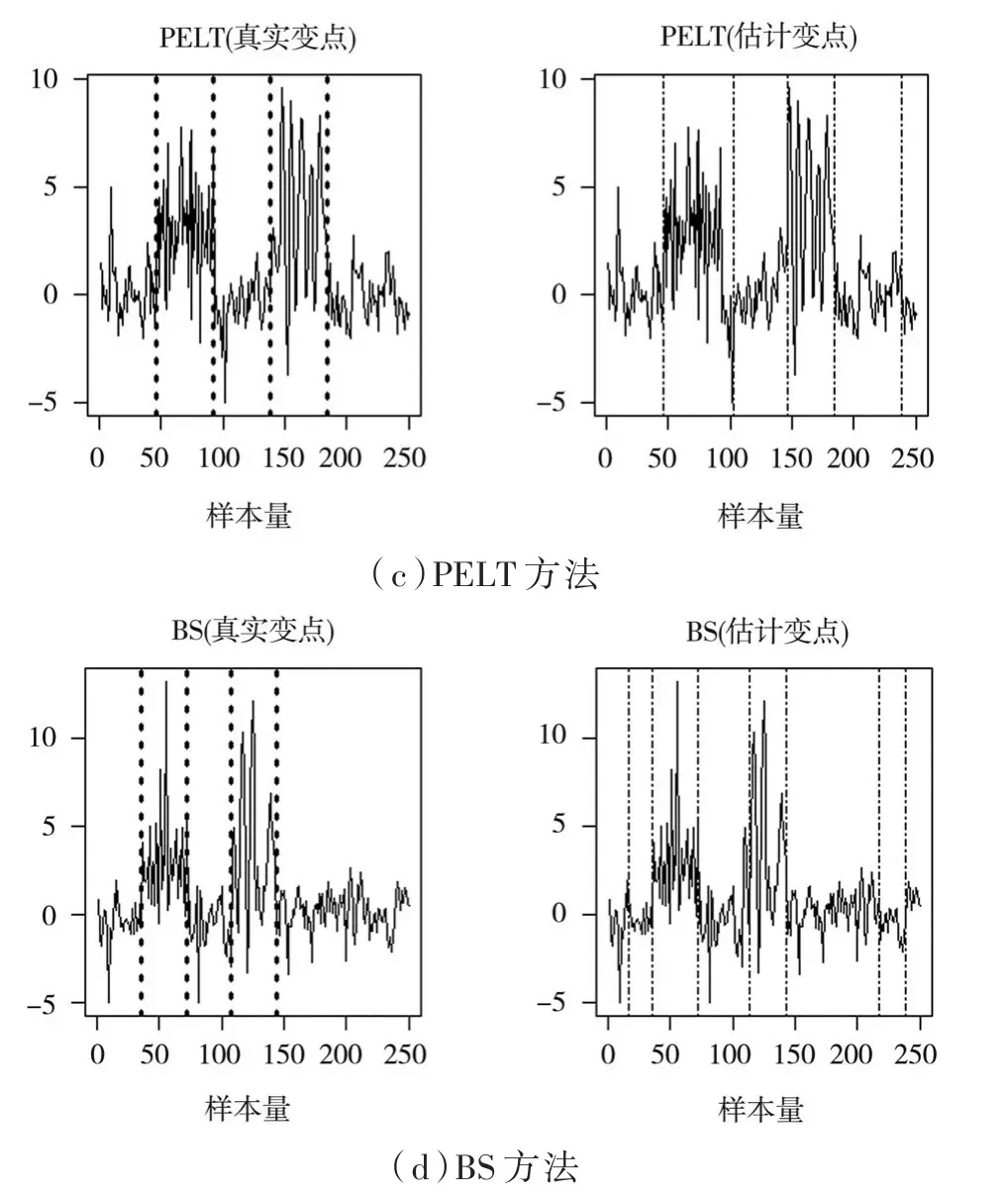
图2 变点估计位置图

表1与表2分别是在场景A下，样本量为1 000时，四种方法测得的真阳率与假阳率。从表中看出，在低水平信号下，HLSM方法的真阳率最高，说明HLSM测得的变点最准确，PELT与BS算法检验效果相差无几，而就假阳率来看，加了准则的HLSM方法最小，说明该方法最稳健，测得的变点几乎都是正确的。在高水平信号下，BS和PELT真阳率较高，但是这两种算法的假阳率也高，说明会把不是变点的值误判成变点。对比低水平信号与高水平信号，变化越大，假阳率的值都有所上升，并且除了BS方法以外，其他三种方法的假阳率也有所降低，说明变化越大，越容易检测出变点值。

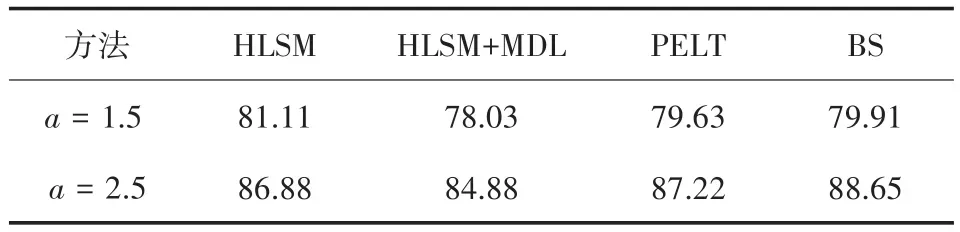
表1 场景A下n=1 000时四种方法的真阳率/%

表2 场景A下n=1 000时四种方法的假阳率/%

表3与表4是在场景B下，样本量为1 000时四种方法的真阳率与假阳率的数值模拟实验结果。对于加入额外方差变化的场景，在低水平信号下，HLSM有着最高的TPR，且假阳率也较低。在高水平信号下，PELT方法的TPR最高，但是假阳率也较高，HLSM的两种方法的真阳率较高，且假阳率很低，综合表现最好，PELT和BS方法虽然有着较高的真阳率，但是假阳率同样很高。

表3 场景B下n=1 000时四种方法的真阳率/%

表4 场景B下n=1 000时四种方法的假阳率/%

表5和表6给出的分别是样本量为1 000时，在加有异常值的场景C中，四种方法真阳率和假阳率的值。从表中能观察到，同一种方法下，高水平比低水平有着更高的TPR，说明变点较大更易检测到变点，且除了PELT方法，其他三种方法的FPR也降低。表5中，HLSM有着最高的TPR，对比PELT和BS能更准确地检测出变点位置。在表6中，加了准则的HLSM方法的FPR最小。结合TPR和FPR分析，HLSM方法检验效果更好，BS和PELT方法会高估变点。

表5 场景C下n=1 000时四种方法的真阳率/%

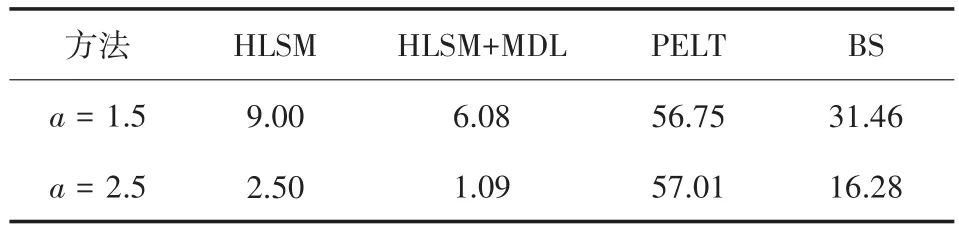
表6 场景C下n=1 000时四种方法的假阳率/%

图3比较了在高水平下（a=2.5），三种场景中不同的方法得到的TPR和FPR折线图，场景A中，左TPR图中观察出，除样本量为1 000下，HLSM比经典的PELT和BS方法有着更高的TPR，在样本量为1 000下，结合FPR观测，PELT的FPR较大，推测PELT的FPR较大是由于高估变点导致。且PELT和BS方法得到每个样本量下FPR的值变化较大，而HLSM两种方法则较平稳。场景B中，同样也是在样本量为1 000时，PELT的FPR最大，但是有着较高的FPR，表示在有额外的方法变化时，PELT和BS算法会高估变点。场景C是加入了异常值的情况，结合TPR和FPR观测，HLSM提出的两种方法检测表现最好，有较高的TPR且FPR较低，不仅能精确地估计变点位置，还不会高估变点值，HLSM的两种方法在异常值存在的情况下，变点检验有着稳健性。在三种场景下，综合TPR和FPR来看，还是HLSM的两种方法有着较优的检验效果。从TPR来看，在高水平下，对比低水平信号和高水平信号的TPR看出，变化越大，就更容易检验出变点值。

图3 高信号水平下：真阳率与假阳率折线图

3 应用

实际数据来自百度地图开放平台2020年8月11日（星期二）长春市生态大街的交通流量数据，数据结构为每五分钟记录一次该路段的车辆速度。将提出的两种HLSM方法应用于交通流数据。

图4（a）为HLSM检验出的变点位置与数量，数量为5，位置分别在41、80、144、180、232。图4（b）为加MDL准则的HLSM检验的变点，数量为3，位置分别在80、144、180。可以看出两种方法都检验出变点80、144和180，对应的时间点为7：45、13：00和16：00，而HLSM 方法则还认为 4：25和21：30也为变点。从检验结果可以看出交通变化的特征，车辆速度在7：45的前后，速度差值较大，很可能因为8月11日是工作日，人们上班早高峰发生了交通拥堵。在7：45和13：00这段时间的车辆速度一直较低，早晨人们上班时间不同，无论是出行旅游还是上班一般都是倾向于上午的时间段，所以上午出行很可能会遇上拥堵。

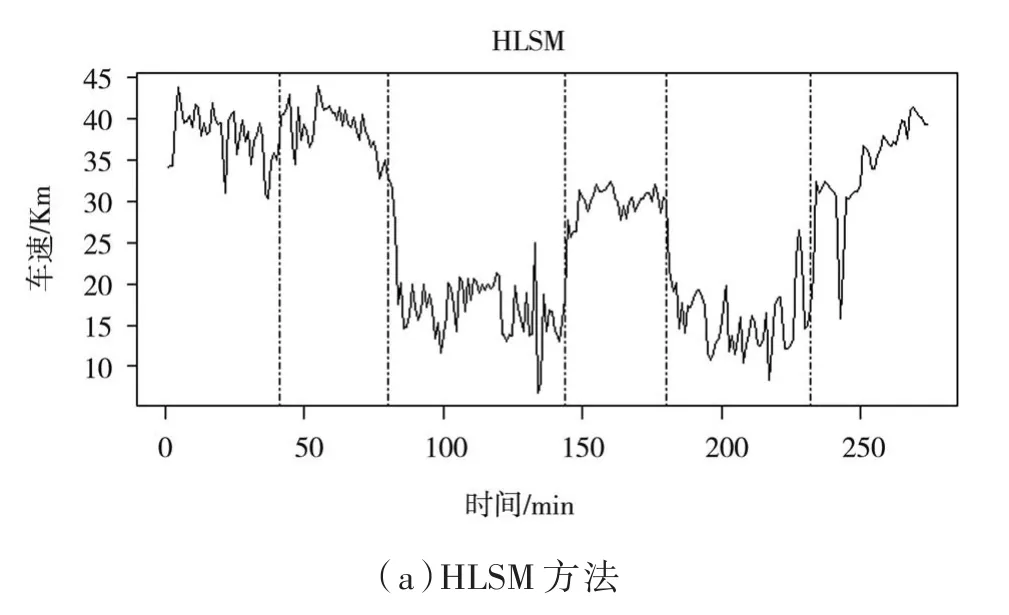
图4 变点检验位置图

在16：00以后，基本为人们下班的时间，下班时间不同，所以能从图中看出，车辆速度较低的状态也是持续了一段时间。对比于上午的早高峰，下午的晚高峰造成的拥堵时间更短。而在21：30之后，基本没有大量的车辆出行，路况良好，车辆也就畅行无阻。

以上的实例分析，证明了所提出的方法在实际应用中的合理性和较强的实用性。

4 结论

本文提出一种基于窗口滑动和Hodges-Lehm‐ann检验的方法——Hodges-Lehmann Scan，识别高斯噪声下的变点。通过数值模拟实验表明，在同方差与异方差的高斯噪声下，认为所提出的新方法能够精确地估计出变点的数量和位置，并且对于有异常值的场景，对比PELT与BS方法显示更好的稳健性。对于在实际问题中出现异常值干扰的情况，HLSM避免一般方法会高估变点的现象。将提出的方法应用于交通数据的实例分析，说明该方法的实用性。