分布式驱动电动汽车转矩分配策略研究

续开轩，韩学辉，李晨晨，孙开蔚，李锐

（长春理工大学 电子信息工程学院，长春 130022）

分布式驱动电动汽车具有车轮驱动转矩独立可控、电机响应迅速且转矩大小精确的优势，更容易实现车辆的稳定性、安全性控制，是电动汽车发展的最佳模式。

针对分布式驱动电动汽车的研究主要集中在车辆行驶稳定性与安全性控制方面。其中Zhang等人［1］针对车辆侧偏角与横摆率误差提出了一种基于模糊逻辑的误差重构策略；Zhao等人［2］将轮胎滑移能量模型用于整体转角控制器（HCC）的整定极大提高车辆在极端条件下的横向稳定性；林程等人［3］基于轮胎纵向力的非线性特征设计了混杂模型预测控制器改善车轮在不同工况下的滑转情况；罗玉涛等人［4］基于转角补偿与转矩分配提出了一种避免极限工况下车辆失稳的后轮转角自适应补偿策略；谢宪毅等人［5］基于路面附着系数调整最优控制的半正定矩阵Q权重系数策略并利用模糊控制理论设计变权重系数调节器，实现了最优控制参数的自适应调整，以改善车辆的稳定性与安全性；金贤建等人［6］为实时观测车辆行驶过程中的车身质心侧偏角等状态及车辆惯性参数，设计了车辆并联双无迹卡尔曼滤波状态参数联合观测系统，并仿真验证即使在重载荷加载条件下该观测器仍具有较高的观测精度；此外诸多学者［7-10］还在车辆电机效率联合稳定性控制等方面展开研究，取得了一些可喜的成果。

1 车辆动力学模型

1.1 七自由度整车动力学模型

目前汽车动学建模应用最为广泛的仍然是七自由度汽车模型，其中七自由度分别包含以X轴为方向的纵向运动、以Y轴为方向的横向运动、围绕Z轴转动的横摆运动外加四个车轮绕Y轴转动的自由度，七自由度模型中轮胎的纵向力与侧向力由魔术轮胎模型计算得出。整车的动力学模型如图1所示。

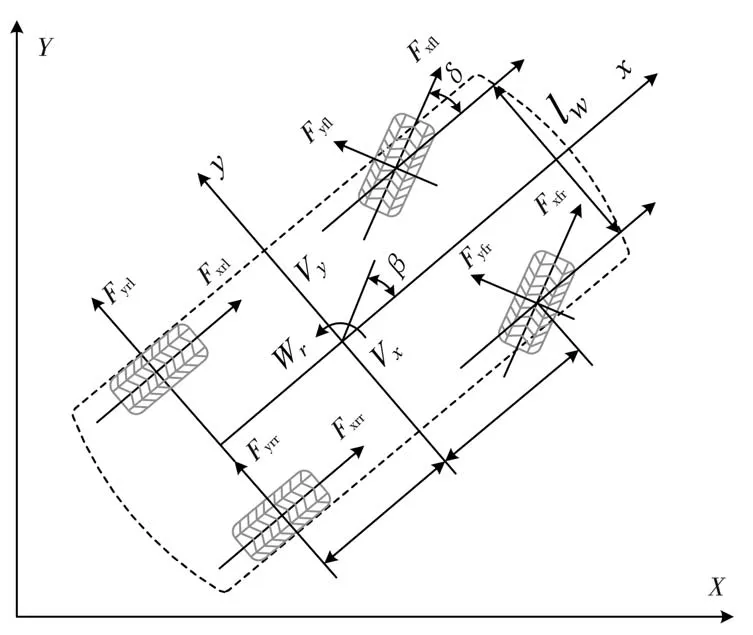
图1 七自由度整车动力学模型

沿坐标系X轴纵向方向的力平衡方程：

沿坐标系Y轴纵向方向的力平衡方程：

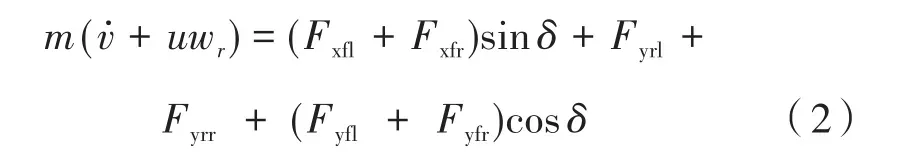
横摆运动方程：

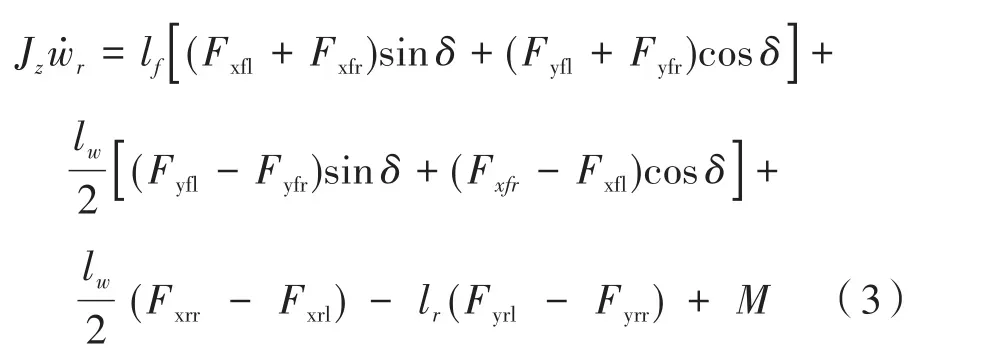
式中，m为车辆质量；δ为施加的前轮转角；lf、lr分别为车辆质心到前轴与后轴的距离；lw为轮距；u̇为车辆纵向速度；v̇为车辆侧向速度；wr为横摆角速度；Jz是车辆绕Z轴的转动惯量；fl、fr、rl、rr分别代表车辆的左前、右前、左后、右后四个车轮位置；M是车辆附加横摆力矩。

1.2 轮胎动力学模型

魔术公式轮胎模型对轮胎力学特性的拟合精度高，是目前汽车操纵动力学研究中最为流行的经验公式之一。轮胎纵向力和侧向力的计算公式为：

车辆的转向会导致轮胎垂直载荷转移，各轮胎的动态垂直载荷表示如下：

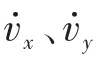
根据车辆纵向与侧向加速度，考虑车辆横摆的影响，轮胎侧偏角为：

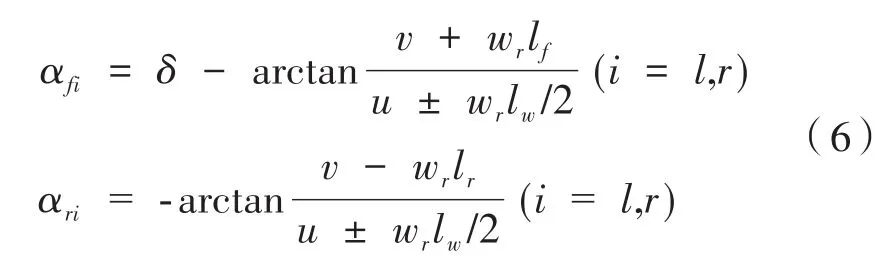
1.3 线性二自由度车辆模型

选取线性二自由度整车模型作为车辆转向过程状态优良的评判标准，即计算横摆角速度与质心侧偏角理想值，图2为二自由度模型。

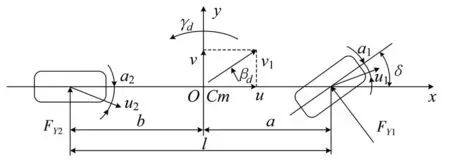
图2 线性二自由度模型

线性二自由度车辆模型的运动微分方程为：

式中，kf、kr分别代表前后轮的侧偏刚度；β为质心侧偏角；a、b是稳定性因子调节系数。

2 质心侧偏角观测器

2.1 卡尔曼滤波算法

质心侧偏角的获取对于提升车辆操纵稳定性尤为重要，目前车辆横摆角速度与侧向加速度可以通过传感器直接测量，但是质心侧偏角无法直接测量，因此质心侧偏角必须通过估算来得到。本文采用卡尔曼滤波算法对其质心侧偏角进行估算。

假设线性离散系统状态方程和观测方程表示如下：

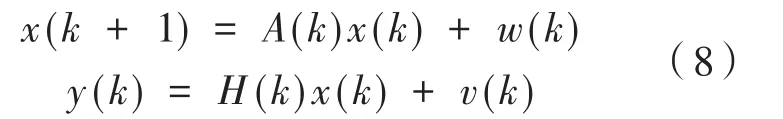
式中，x(k+1)是系统n维状态向量；A(k)是系统状态转移矩阵；y(k)是系统m维观测向量；w(k)为系统随机噪声；v(k)为系统m维观测噪声；H(k)为观测矩阵；假设w(k)、v(k)为互相独立且正态分布的白噪声；系统的随机噪声、观测噪声协方差矩阵为Q、R，卡尔曼滤波算法具体步骤如下：

（1）状态一步预测：

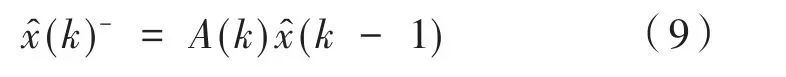
（2）状态估算计算：

（3）滤波增益矩阵：

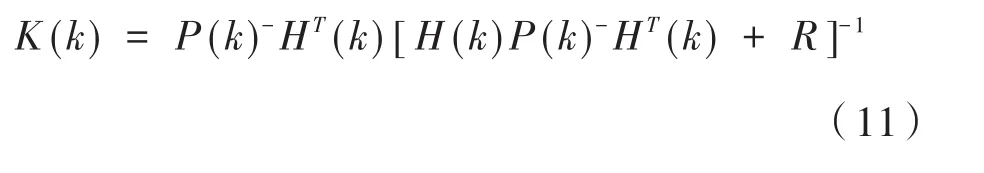
（4）一步预测误差方差阵：

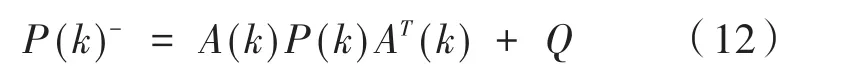
（5）估算误差方差阵：

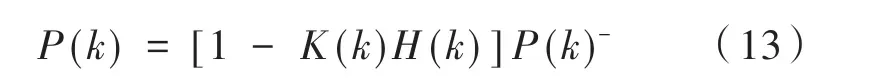
2.2 质心侧偏角观测器设计

对线性二自由车辆模型的运动微分方程进行离散化处理可得：

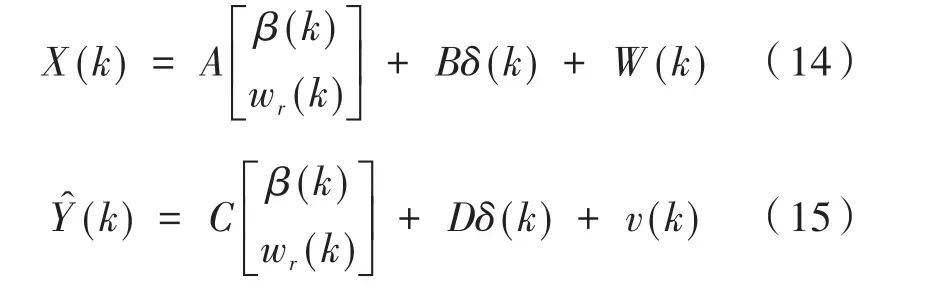
其中：

将上述公式带入卡尔曼滤波器，给定初始值就可以根据观测值递推计算得到质心侧偏角的估算值。

3 转矩分配分层控制器设计

设计分层控制器改善车辆操纵稳定性，图3为其流程图，上层控制器利用滑模控制方法，将质心侧偏角与横摆角速度理想值与实际值作为输入，求出横摆力矩期望值；下层控制器基于横摆力矩期望值，采用粒子群算法对转矩进行优化分配。

图3 控制流程图

3.1 上层控制器设计

选取滑膜切换函数为令其跟踪质心侧偏角与横摆角速度理想值，其理想值为线性二自由度车辆模型计算得到：

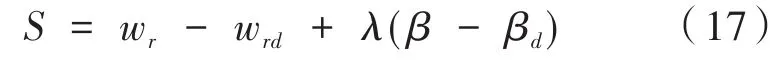
由式（17）微分可得：

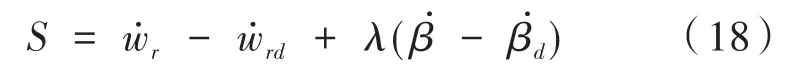
将式（3），即七自由度整车动力学方程的横摆运动方程，整理代入式（18）可得：

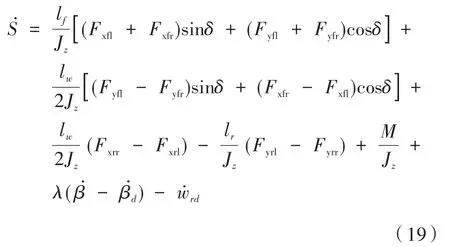
选取指数趋近律，并采用更为优化的饱和函数sat(s/a)替换符号函数sgn(s)用以削弱抖振带给系统的影响：

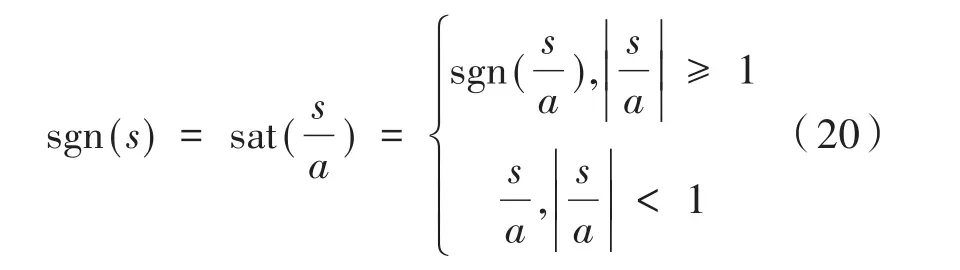
式中，ε、k、a分别代表系统趋近滑模面时的速度与到达滑模面后系统的收敛速度以及滑模面厚度。

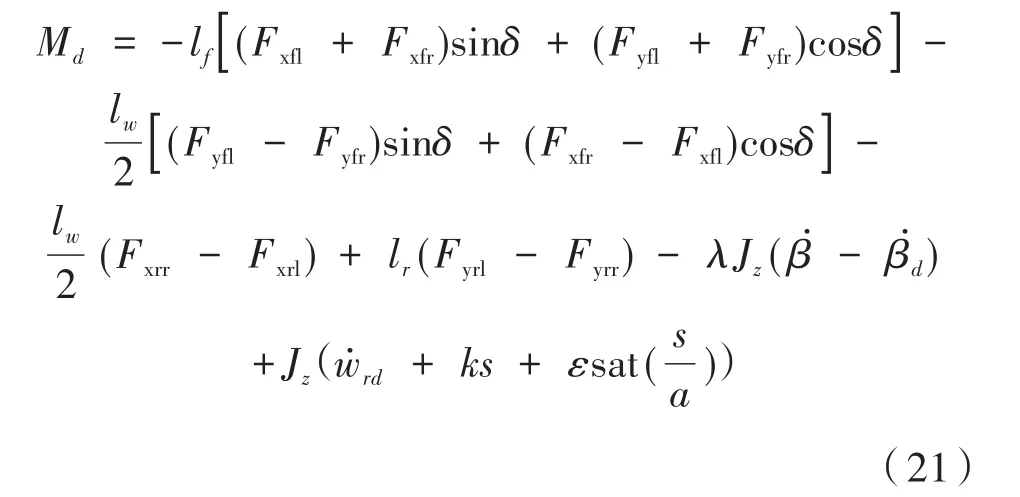
3.2 下层控制器设计

整车控制系统结构图如图4所示。

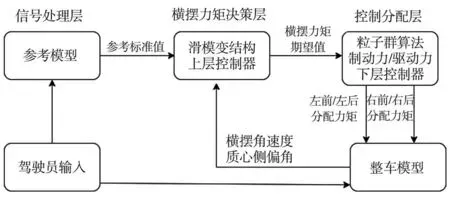
图4 整车控制系统结构图

根据七自由度整车动力学模型的力平衡方程与横摆运动方程，可推导出每个车轮所分配转矩的纵向力与横摆力矩可表示如下：

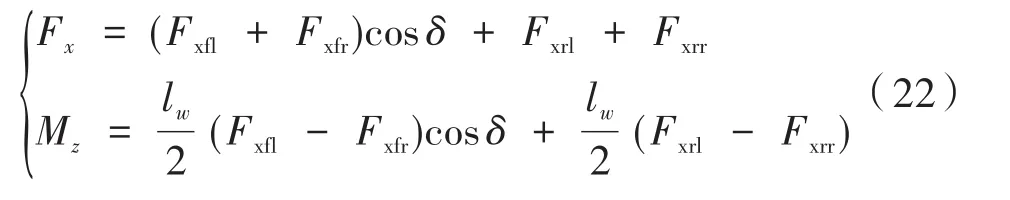
式（22）可表示为如下矩阵形式：

式中：

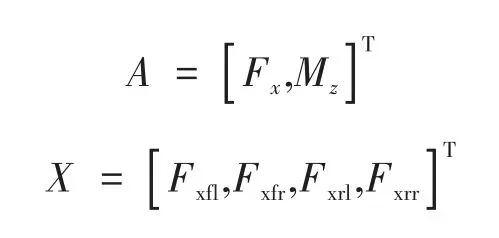
轮胎负荷率是表征车辆稳定性的重要参数，其值越小表示轮胎可利用的附着力越大，即车辆维稳能力越强，且轮胎纵向力与侧向力具有耦合关系，侧向力无法直接控制，故选取轮胎最小负荷率作为优化分配的控制目标，其控制函数表示如下：

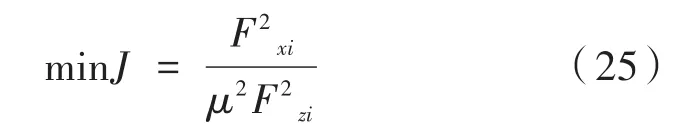
式中，Fzi为轮胎动态垂直载荷；μ为路面附着系数。

综上，将转矩分配优化问题描述为如下约束条件下求解最优值形式，再利用粒子群优化算法进行求解：

将上式转换为求四维向量且存在约束条件的粒子群算法进行求解，粒子群算法速度和位置更新公式为：

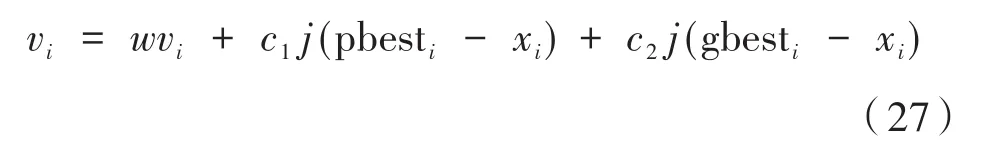
式中，c1、c2为学习因子设为2；惯性权值w设为0.8；初始化种群个数与最大迭代次数设为70，粒子群算法流程如图5所示。

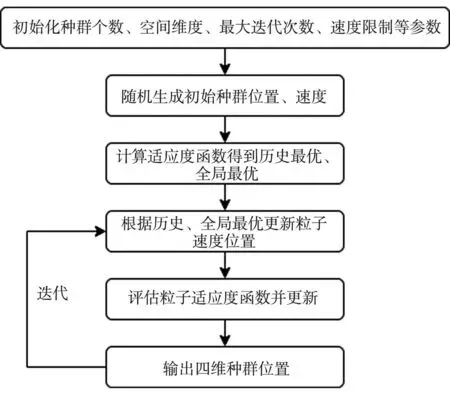
图5 粒子群算法流程图

4 仿真分析

为了验证上述分层控制器的有效性，在MATLAB/Simulink环境下搭建整车七自由度动力学模型、二自由度线性模型、质心侧偏角观测器与分层控制器，工况设定为移线仿真与J-turn仿真，车辆仿真参数数据如表1所示。

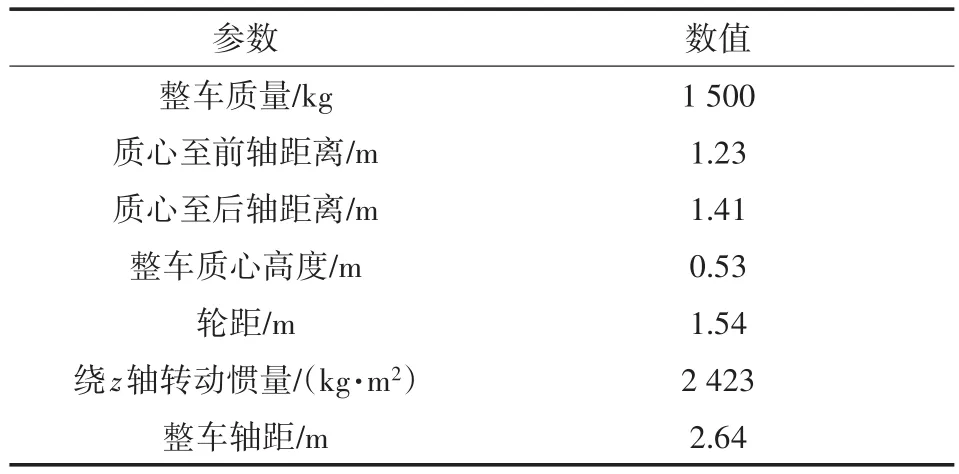
表1 整车参数

4.1 移线仿真

给定车辆行驶速度为50 km/h，令前轮转角为5°的正弦输入，周期为10 s，给定驱动转矩为300 N，路面附着系数设为0.6。

从仿真图中可以看出在移线工况下，经过分层控制器转矩优化分配后，图6所示的车辆横摆角速度与图8所示的车辆质心侧偏角均得到了较好的抑制，收敛速度与迟滞均得到了不错的改善，并能很好地跟踪其理想值。图7为轮胎利用率，从中可以看出其大小得到很好的控制，使车辆留有充足的稳定性裕度。图9为转矩分配结果，从中可以看出车辆外侧、内侧均可以按照预期增加一定的驱动力矩与制动力矩。说明车辆具有很好的循迹效果以及稳定性控制。

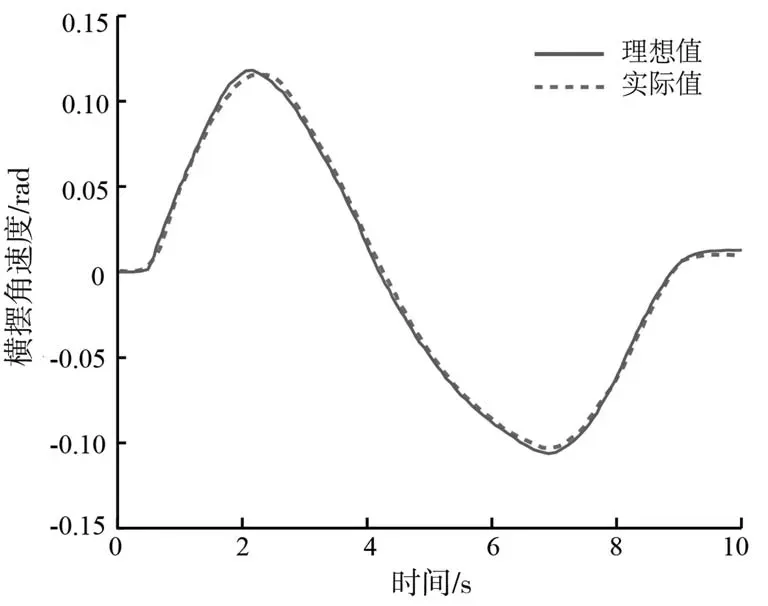
图6 横摆角速度

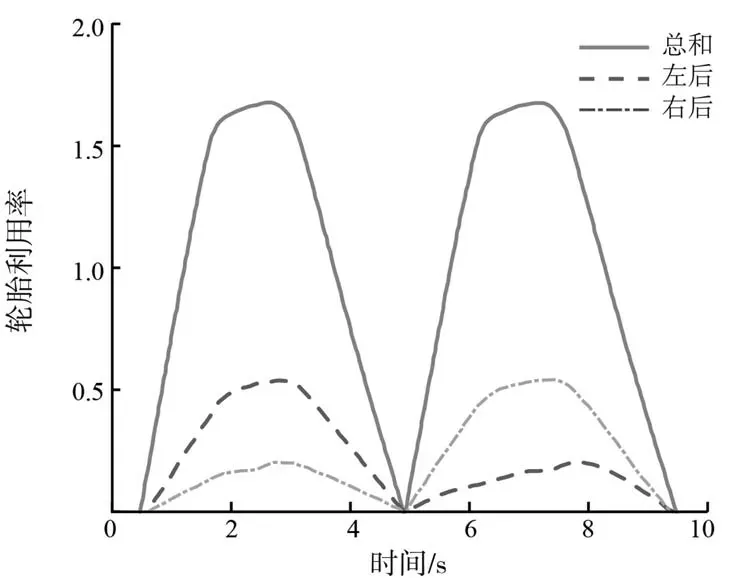
图7 轮胎利用率

图8 质心侧偏角

图9 转矩分配

4.2 J-turn仿真

为了更好地验证设计控制器在不同工况下的控制效果，将前轮转角输入换为5°的阶跃输入，其余条件不变。

从中可以看出在J-turn工况下，图10所示的车辆横摆角速度与图12所示的车辆质心侧偏角同样可以很好地跟踪其期望值，并且收敛速度与迟滞也表现良好。从图11所示轮胎利用率总和与图13所示转矩分配结果可以看出，该控制策略可以在降低轮胎利用率的同时很好地实现转矩的分配效果，让车辆内外侧在阶跃工况下也能很好地分配制动力矩与驱动力矩。说明在阶跃工况下该策略同样可以实现车辆的稳定性控制，证明了所设计控制策略的有效性。

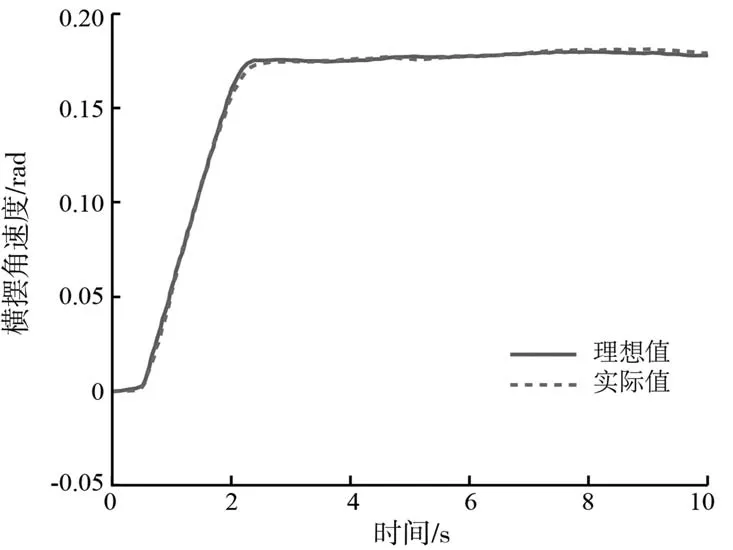
图10 横摆角速度

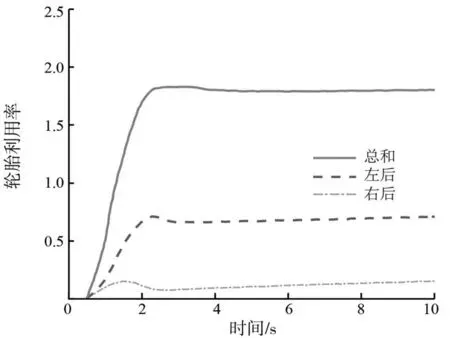
图11 轮胎利用率

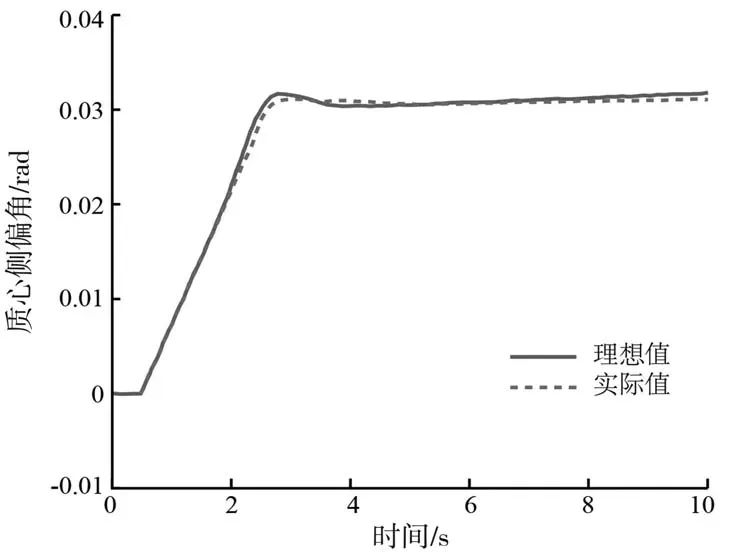
图12 质心侧偏角

图13 转矩分配

5 结论

本文利用分布式驱动汽车转矩独立可控的特点，设计了分层控制器，上层控制器采用滑膜控制的方法计算其期望横摆力矩，并基于其横摆力矩的值设计下层控制器，使其在轮胎最小负荷率条件下，构建其约束条件，针对其转矩分配值难以获取的特点，利用粒子群算法对其优化求解。

仿真利用Matalab/Simulink建立了七自由度整车模型、二自由度线性模型以及利用卡尔曼滤波算法实现的车辆质心侧偏角观测器，并基于此进行了移线以及J-turn工况下的仿真。仿真结果可以看出，车辆的横摆角速度与质心侧偏角均能很好地跟踪二自由度模型计算的期望值，并且轮胎负荷率也得到了很好的控制，给整车稳定性控制留有更多的裕度，并且转矩分配结果也能看出，车辆在不同工况下均能按照预期进行车辆内外侧的制动力矩与驱动力矩分配。

仿真结果证明了该控制器设计的有效性，可以很好地提高车辆的操纵稳定性与安全性。未来还可以针对新能源的需求，对车辆电动机或发动机进行能量效率曲线的优化，进一步完善该研究。