基于深度卷积生成网络的冲击波信号压缩感知方法

豆佳敏，王琰，王义君

（长春理工大学 电子信息工程学院，长春 130022）

火炮等武器在发射试验中所产生的冲击波，会对周围测试人员的身体及仪器设备造成严重危害。因此，准确地测量炮口冲击波压力信号数据，成为武器研制和改进的一个重要环节［1-2］。由于冲击波信号频率成分复杂，且含有高频分量，导致基于奈奎斯特（Nyquist）采样原理采集冲击波信号时须保持高采样率，进而产生海量数据，对系统的数据传输、存储和处理造成不必要的压力［3］。为突破 Nyquist限制，2006 年Donoho D L等人［4］提出压缩感知（Compressed Sens‐ing，CS）理论，该理论提出，可以以低于信号最高频率的二倍进行数据采样并恢复出原始数据。由于冲击波信号中的有效信息在整个采集时段比重很小，即存在某个稀疏域对信号可以稀疏表示，故应用压缩感知技术对该信号进行压缩采样及重构处理。它已用于语音处理、冲击波信号处理［3］等多个领域，基本基于常用的稀疏字典——离散傅里叶基（Discrete Fourier Transform，DFT）和离散余弦基（Discrete Cosine Transform，DCT）进行研究的。然而，信号的稀疏表示主要是人为选取的，在相对复杂的情况下容易忽略不同数据之间的依赖性和稀疏矩阵的自适应性［5-6］，如何设计出一个自适应的稀疏矩阵或者不用设计稀疏矩阵就可以恢复出原始信号是一个值得研究的问题。

深度学习（Deep Learning，DL）是近年来一个新兴领域，尤其是生成对抗网络（Gene-rative Ad‐versarial Nets，GAN）已经广泛应用于语音识别、机器翻译［7-8］、图像分类及识别［9］、人脸识别［10］、手写字体识别［11］等多个领域。其中，深度学习主要涉及学习数据的多个表示形式以及更高级别的抽象表示，研究神经网络从欠采样随机线性测量信号中恢复出原始信号的性能［12］；生成网络学习从低维表示空间到高维样本空间的映射，在训练时，鼓励这种映射产生与训练数据集向量相似的向量。由于采用压缩感知技术处理冲击波信号时要求信号为稀疏的，不仅稀疏矩阵设计困难，而且信号重建过程为寻找欠定线性方程组的最稀疏解的过程，属于NP难问题。因此，Bora等人［12］提出深度生成模型，将CS与单独训练的神经网络生成器相结合，验证了该模型可以用作图像的先验条件以解决CS技术中的稀疏先验，直接恢复出原始图片。Rosca等人在Bora的基础上加入元学习来训练生成函数进而优化信号重建过程［14］。以上研究都是应用于图像领域，只有少数研究者通过深度学习思想处理一维信号，文献［17］提出堆栈去噪自编码器的方法应用于超宽带回波领域，目前，尚未发现研究者将深度学习思想应用于冲击波信号领域。为此，本文结合深度学习中的深度卷积生成对抗网络（DeepConvolution Generative Adversarial Nets，DCGAN）中的生成网络（Generative Nets，GN）部分，利用生成网络的拟合能力，避免压缩感知中对稀疏矩阵进行人为设计的问题，通过对每一个信号进行单独的学习，进而实现信号端到端恢复。

1 理论分析

1.1 压缩感知

图1为压缩感知技术采样流程图。

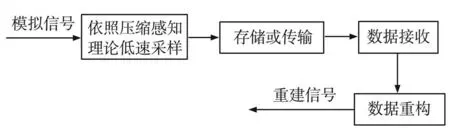
图1 压缩感知采样流程

图1可以看出，压缩感知技术一开始就扔掉冗余数据，来节省数据采集时间和存储空间。该技术需要满足两个前提条件：（1）信号在某种稀疏矩阵下须满足信号稀疏性，即信号的非零元素远小于信号的总长度；（2）观测矩阵满足约束等距条件，即观测矩阵和稀疏表示基不相关。因此，信号稀疏表示作为压缩感知技术的前提条件，当信号x∈RN在时域中存在K个非零值，不满足K≪N时，需要设计一个N×N的稀疏基Ψ，使得x在Ψ域上稀疏：x=Ψθ，其中θ为x的稀疏向量。常见的稀疏基为DFT和DCT，它们都是固定的。测量矩阵的选择也是必要环节，本文选取最常用的高斯随机独立矩阵Φ∈RM×N（M≪N），在Φ下的线性投影为y=Φx=ΦΨθ=Aθ，其中y∈RM，A为传感矩阵。信号重构为压缩感知过程中的核心环节，最直接的方法是采用l0范数求解，但该求解方法属于NP难问题。所以，采用l1范数来逼近l0范数进行求解，如式（1），其中ε为一个非常小的常数：

通过以上步骤就可以从被测信号中恢复出原始信号，且可以发现l1范数求解只适合稀疏表示后的信号。所以，不少学者通过对稀疏字典进行研究，以使变换后信号足够稀疏，但对于不同的信号设计不同的稀疏矩阵比较麻烦，常用的稀疏矩阵在一维信号中性能不一定好。本文的冲击波信号虽在稀疏基DFT和DCT上为稀疏信号，但是稀疏基对信号的稀疏程度也存在差异，进而影响信号重构误差。

1.2 生成对抗网络

本文将深度卷积生成网络与压缩感知（Deep‐Convolution Generative Nets Compressed Sensing，DCGN-CS）相结合，避免使用l1范数恢复信号和稀疏矩阵的选取工作。DCGAN是生成对抗网络的一种演变，生成对抗网络核心思想来源于博弈论的纳什均衡，它设定参与游戏的双方分别为一个生成器和一个判别器，生成器的目的是尽量去学习真实的数据分布，而判别器的目的是尽量正确判别输入数据是来自真实数据还是来自生成器［13］。图2为生成对抗网络的工作流程。

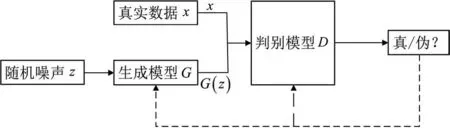
图2 GAN工作流程

图2中，生成器的输入为随机信号z∈(0 ,1)，判别器的输入为真实数据x和生成器中生成的数据。用可微分函数D和G分别表示判别器和生成器，G(z)则为由G生成的尽量服从真实数据分布Pdata的样本，判别器D的目标是实现对数据来源的二分类判别：真或伪，两者相互对抗并迭代优化的过程使得D和G的性能不断提升。最终，当判别器D的判别能力提升到一定程度，依然无法正确判别出数据来源时，则可认为该生成器G已学习到真实数据分布。

2 基于深度卷积生成网络的压缩感知算法

2.1 DCGN-CS算法设计

深度卷积生成对抗网络的生成网络在学习原始信号被压缩采样得到的数据之前，可以优先学习到信号“没有被损坏的原始部分”［14］，换句话说，卷积网络可以训练信号的先验知识，这种先验知识不是通过大量样本获得的，而是通过卷积网络结构本身获得的［15］。此外，该网络模型是一种端到端的数据处理模型，避免传统压缩感知中稀疏字典的设计。所以，本文引入深度卷积生成网络，得到基于DCGN-CS算法原理图如图3所示。

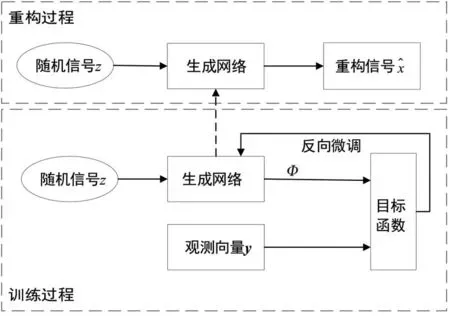
图3 DCGN-CS算法原理图

由上图可看出，生成网络处理数据的能力可以近似看作任意函数计算过程。本文引入深度卷积生成网络直接通过随机信号恢复出原始信号，它的工作过程与压缩感知技术很类似，所以将两者结合起来，建立一个深度卷积生成网络与压缩感知技术相结合的算法模型。定义函数如下：

式中，Φ为行列是M×N（M×N）的独立同分布的高斯随机观测矩阵；Φ中的元素ϕi,j是随机独立的变量，并且服从期望为0，方差为1/n的分布；G(z;w)为生成网络的输出结果；z是一个固定的随机信号；w为神经网络中的权重值；ς为观测信号中的噪声。因此，该式的目的就是使G(z;w)的结果和原始信号x尽可能相似。通过设计损失函数来训练神经网络，其表达式如下：

当资产超过7位数，并稳步向8位数迈进时，孟导的人生追求也逐渐从“利”转向了“名”。要璀璨，要光彩夺目。孟导这时的心境和这么一句台词不谋而合。无奈孟导本人虽然在导演领域有所擅长，但是气质、天资平平，从他目前还是单身的钻石王老五这点上，就能看出很多问题。好在孟导在他执导的影片里看多了风花雪月，单身生活，也很满意。

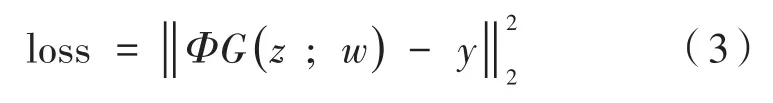
采用上式最小化损失函数，微调网络中的参数，得到最合适的网络参数值w。最后，通过深度卷积生成网络的输出结果G(z;w)得到重构

数据。因此，DCGN-CS是通过训练生成器样本数据的输出值乘以观测矩阵的结果与观测向量之间的误差，采用梯度下降的方法来优化网络权重参数，使损失函数的结果尽可能小，进而使生成器的输出样本值和原始数据尽可能相同。

2.2 DCGN-CS算法实现过程

本文涉及的生成网络是采用深度卷积生成对抗网络中的生成器部分，它的优点主要有：（1）使用分数步长卷积代替了池化层，使生成器能够有效避免数据信息的损失。例如，输入为3×3矩阵，同样使用了3×3过滤器，反向步长为2×2，故在每个输入矩阵之间填充一个0，最终输出为5×5。（2）对于生成器的输出层使用了Tanh激活函数tanh(x) =2σ(2x) -1，该函数可以把数据压缩到-1到1的范围，避免了Sigmoid函数均值不为0的问题。其他层均使用了ReLU激活函数，该函数计算公式简单，表达式为：f(x)=max(0 ,x)，且在随机梯度下降中比Sigmoid和Tanh更加容易使得网络收敛，这样可以让模型更快地进行学习，且能避免梯度消失的问题。（3）使用批量标准化。深度学习中的神经网络层数很多，每一层都会使输出数据的分布发生变化，随着层数的增加，网络的整体偏差会越来越大，批量标准化可以有效使得数据服从某个固定的数据分布，且可以加速网络收敛。因此，深度卷积生成网络的结构为由全连接层和分数步长卷积层组成。其整体结构图如图4所示。

图4中，输入层为一个全连接层，输入数据为100维的随机数据z，服从范围在[- 1,1]的均匀分布，输出4×4×1 024的一个矩阵，之后经过一系列分数步长卷积后，形成64×64×3的图片。

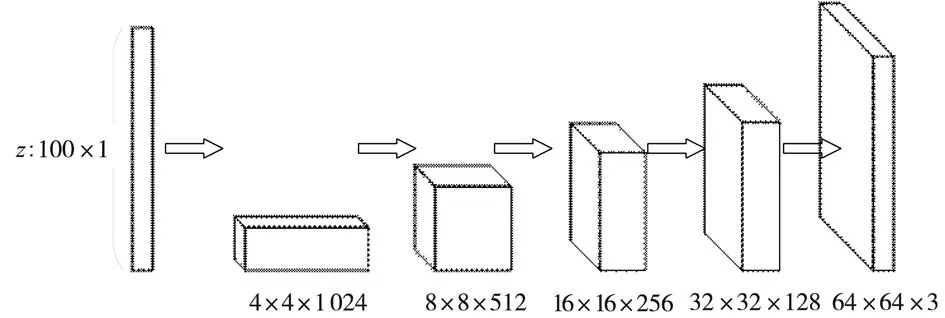
图4 DCGN结构图

与传统的数据处理方法相比，本文将用到图像处理方法对一维数据信号进行处理，其宽度将设置为1，长度为一维信号的长度。传统一维数据处理过程中的卷积公式为：

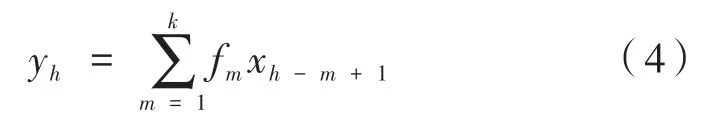
式中，fm为过滤器；k为滤波器的长度。将上式进行变换，得到一维信号类似于图像处理的卷积表达式，如下：

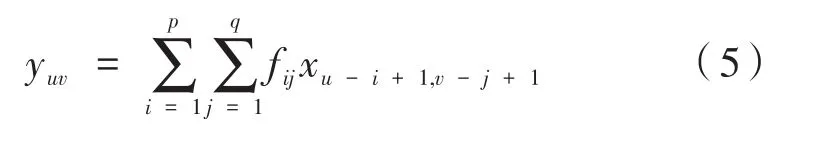
式中，fij为过滤器，在深度卷积生成网络中的每一个卷积层中需要假设有零填充。因为，在深度卷积生成网络中将会用到分数步长卷积的操作，分数步长卷积的操作结果应该是输出层的宽度和长度大于输入层的宽度和长度，要使输出层的长度为1，这显然是不可能的。

3 实验数据处理结果

3.1 实验平台

本文进行实验的计算机配置：处理器为英特尔Xeon E5-2690v4，主频2.6 GHz；显卡为NVIDIA GeForce RTX2080Ti，显存为 11 GB；编程环境为PyCharm；深度学习框架为TensorFlow；编程语言为python。

3.2 建立DCGN-CS所需数据集及参数设置

实验数据采用冲击波数据信号，信号来源为某型火炮发射时产生的冲击波信号。采用15 psi和5 psi量程传感器在火炮发射瞬间对冲击波信号进行采集，得到上升沿陡峭、高超压峰值、正压作用时间短、负压恢复时间长的冲击波数据，其有效信息是在整个采集时段比重很小的非平稳随机测试数据。在实际实验中对每一组冲击波信号进行预处理，首先从每个冲击波信号的第500个点开始，共截取4 096个点的长度，接着对信号进行了归一化操作，最后对其进行实验分析及讨论。

本文设计的DCGN-CS算法，是基于Tensor‐Flow框架实现的。首先，将初始信号设置为均值为0，方差为0.01的一个4 096×1的正态分布向量。其次，添加4层分数步长卷积层，每一层的移动步长分别为1、2、2、1。最后，设置全连接层的均方差为0.02，均值为0。在损失函数中使用Adam［16］优化器，设置初始学习率为 0.001，动量参数β1为 0.5，β2为 0.55。其中，学习率是一个自适应学习的变化量，随着迭代次数的增加会逐渐减小。

3.3 实验结果分析

针对本文选取的冲击波信号，观测点数M取1 200时，分别使用DCGN-CS算法、DFT-OMP算法、DCT-OMP算法对观测信号进行重构。其中，DCGN-CS算法迭代120次。其仿真结果实验对比图如图5和图6所示。

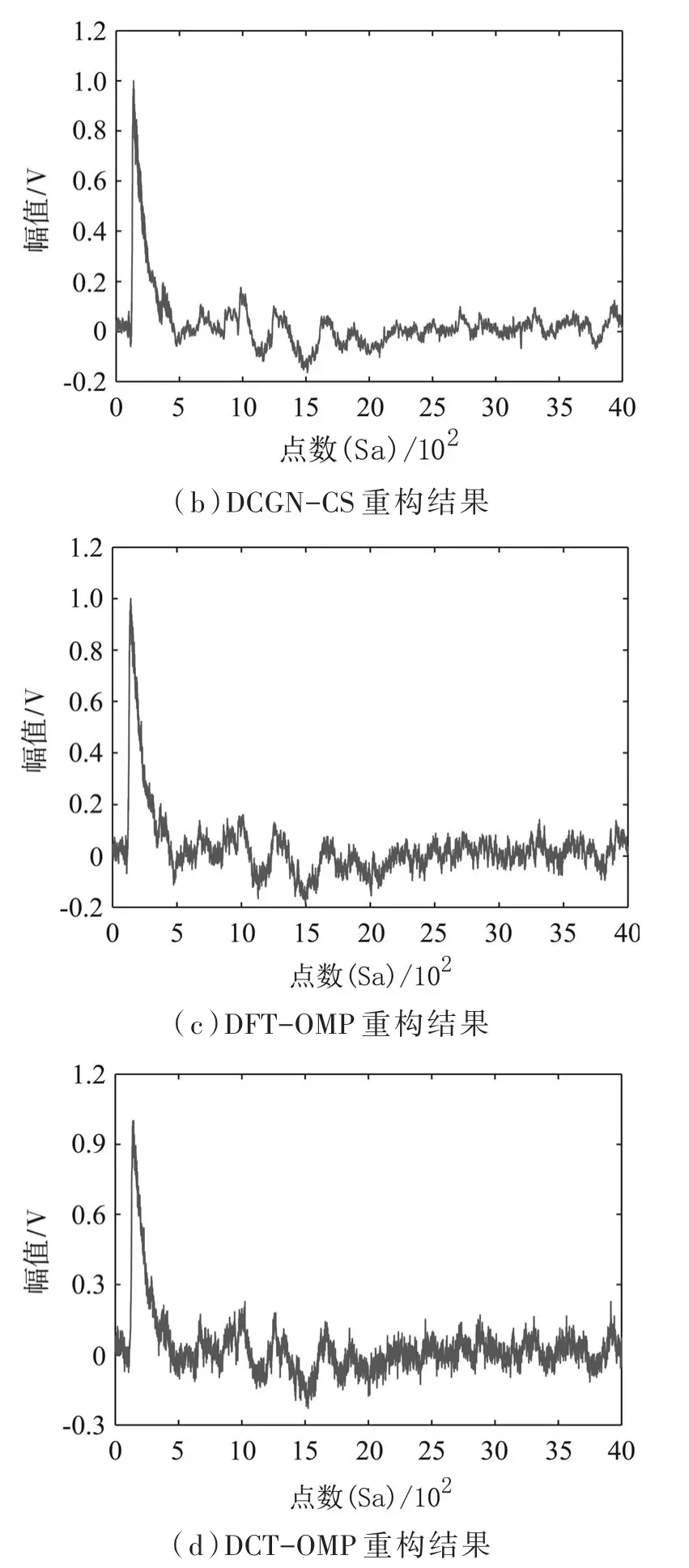
图5 不同算法对15 psi传感器实测冲击波信号重构结果图

图5和图6可以直观地看出，与传统方法相比，本文设计的算法能够比较好地重构出冲击波信号。为了进一步比较本文设计的算法在不同观测点数的重构效果，设置观测值M的长度为800、1 200、1 600、2 000、2 400、2 800，分别进行50次模拟实验，通过式（6）所述的均方根误差（Root Mean Square Error，RMSE）来比较不同测量值下三种算法的误差变化。

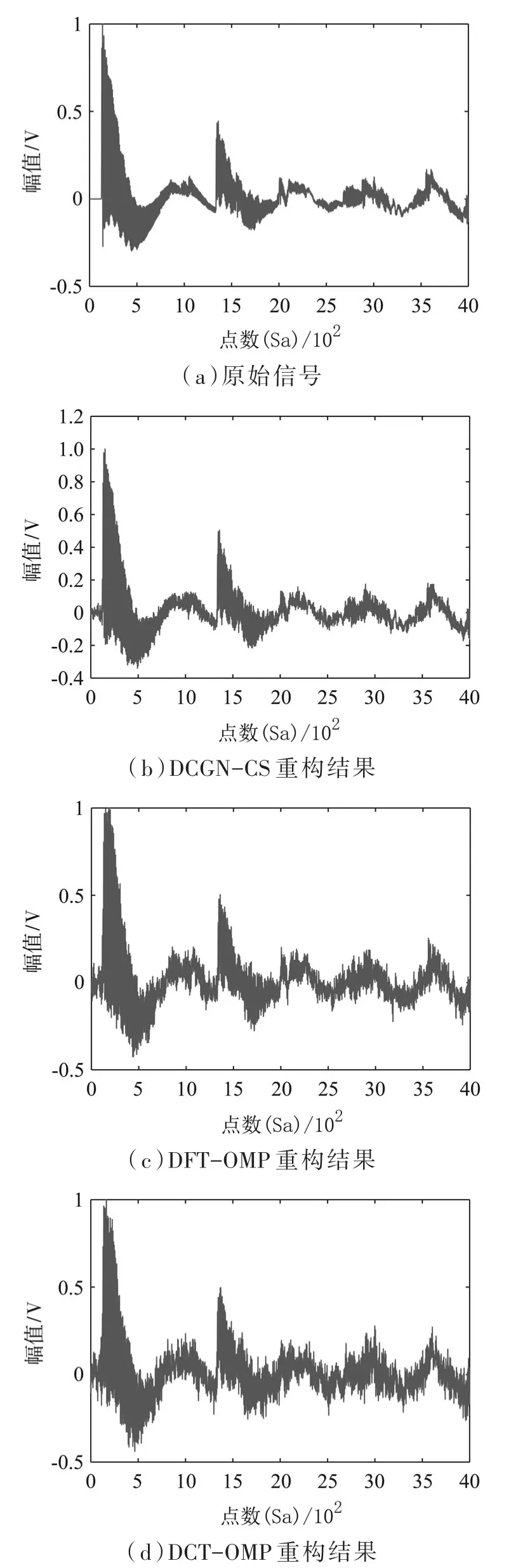
图6 不同算法对5psi传感器实测冲击波信号重构结果图

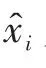
图7和图8可以看出，在两种测试数据下，本文设计的算法在观测值较小时，没有DFT-OMP算法好，这是因为观测值小时，数据中包含的冲击波信号特征值少，该算法的重构结果受数据特征影响很大，所以，在观测值小时不具备优势，进而影响到信号重构误差值。相反，传统压缩感知技术在重构算法相同时，信号重构误差主要受信号稀疏度的影响，本文在选取的两种稀疏基下对冲击波信号的稀疏表示结果存在差异，因此，影响重构误差值。然而，随着观测点数增加，DCGN-CS算法的RMSE值急速下降。当观测点数大于1 200时，DCGN-CS算法已优于两种传统算法。最后，DCGN-CS算法的RMSE值稳定到一个较小值时约为DFT-OMP算法和DCT-OMP算法在M为2 400时误差值的0.5倍。

图7 15 psi传感器实测数据在不同算法下测量数M与重构误差关系

图8 5 psi传感器实测数据在不同算法下测量数M与重构误差关系

4 结论

本文引入深度卷积生成网络与压缩感知相结合的算法应用于冲击波信号测试领域，解决了传统压缩感知技术在处理冲击波信号时稀疏矩阵不易设计，及其对重构结果影响的问题。该算法避免了求解信号稀疏表示的问题，通过对每一个信号进行单独学习，利用损失函数对网络中的参数进行优化，实现信号端到端的恢复。仿真结果表明：在观测点数大于1 200时，本文算法相比于传统压缩感知技术能更好地恢复出原始冲击波信号；在不同观测值下对三种算法进行重构误差比较，DCGN-CS算法在误差值稳定到一个较小值时约为DFT-OMP算法和DCT-OMP算法在M为2 400时误差值的0.5倍。