让学生的思维在探寻点线之间的规律中发展
2022-03-07刘艳
刘艳
数学思维能力的培养是数学教学的核心。小学数学教学应该遵循学生的认知规律,拓宽思路,发展思维,让学生主动获取知识。小学生的思维以具体形象思维为主,抽象逻辑思维为辅,他们生性好奇,乐于模仿,什么事都喜欢动手试试。因此,教师要依据教材特点,有意识地投其所好。在小学四年级的数学教材“线与角”这一章节中,点与线的教学占据很大比例。如果教师能结合教材,帮助学生理解点线之间的规律,就可以有效培养他们的思维能力。
一、结合生活案例,让学生具备空间思维
在生活中,学生会应用到一些数学知识,然而他们受到数学理论知识缺乏的局限,没有深入理解这些内容,导致在学习数学时受到负面影响。例如,在学习“点与线”的知识时,学生就会犯下此类错误,因此教师在开展教学前,要先做好教学预测,结合生活中的案例,让学生理解实际生活与数学概念直线之间的联系,促其学会应用空间思维掌握点与线的相关概念。
如在上课时,教师手里拿一根毛线,同时在黑板上画一条直线,让学生理解生活中的直线和数学几何中直线的差异。通过辨析,学生会发现在生活中人们探讨一根直线,会探讨“它是什么颜色、多长、多粗”等。而在数学中,学生不探讨直线的颜色、粗细,他们会默认“直线就是两端无限延长的线,它没有端点”。应用同样的方法,教师引导学生辨析生活中的一个点和数学中的一个点的差别。通过探讨,学生明确了只需要探讨点、线的空间属性和性质,不需要探讨与数学内容无关的问题。
二、应用数学案例,让学生具备抽象思维
小学生的抽象思维能力较弱,他们有时难以从抽象的角度来思考数学问题,所以教师在开展教学时,要引导学生辨析相似的数学概念。当学生可以结合相似的数学概念进行思考和分析,并能发现数学概念的异同后,他们便能从抽象的视角掌握数学概念的内涵。
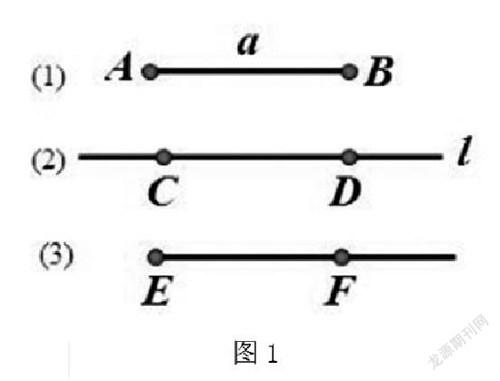
例如,教学“直线、射线、线段”的概念时,有的学生一时难以理解这三个概念之间的差异,教师就可以引导学生进行画图,让学生从定义、图形表示、区别(包含端点、是否可延伸、是否可测算)来分析这三个数学概念的异同。学生可以结合图1,分析图形中哪些是直线,哪些是射线,哪些是线段。借此,学生可以归纳出线段的定义、图形表示的方法、有无端点,能否延伸、能否测算等。同理,学生也能归纳出直线、射线的定义。经过分析,学生在学习“线”的知识时,会更加深刻地理解直线、射线、线段的概念。
三、结合“点与线”的关联,优化学生的思维模式
部分学生在学习“点与线”知识时,存在被动学习的心理,他们不能从中挖掘出大量的数学知识。而有些学生则有着强烈的好奇心,他们能够针对点与线的知识提出许多数学问题,继而他们会为了解决问题进行深入探究。在开展“点与线”的教学时,教师需要引导学生积极探索,并在探索的过程中培养他们的发散思维。当学生能够应用发散思维链接知识后,教师再培养其归纳思维,使学生能够在整合发散思维中获取知识,探索知识的规律,形成具体的知识体系。
1.发散思维
在教学中,教师要引导学生应用发散思维来思考问题,使学生能够由此及彼地掌握知识,进而促其发散思维得到进一步夯实。例如,教师引导学生把点线的知识与以往学过的几何知识结合起来,学生便会思考“一个点存在对称轴吗?”教师让学生积极探索这一问题。有的学生认为,点是轴对称图形,也是中心对称图形。随后,教师让学生分析轴对称图形和中心对称图形的概念。通过学习,学生发现从几何学的意义而言,点没有构成图形,于是一个点既不构成轴对称图形,也不构成中心对称图形。在提问学生的启发下,其他学生开始思考:直线、射线、线段是轴对称图形还是中心对称图形?其理论依据是什么?在探讨的过程中,学生对几何知识概念的理解更加深刻。
2.分类思维
在学生掌握了大量数学知识以后,教师引导学生应用绘制概念图的方法,将知识进行分类,使学生能够把掌握的知识进一步条理化、系统化。在教师的引导下,学生提出以下分类:线是由点构成的,无数个点可以构成线;将点构成的线按形态进行分类,可分为直线、折线、弧线、曲线等;点又可以构成射线、线段等,这些线的端点存在差别。教师引导学生将知识进行科学分类,学生便建立起了完善的知识体系。
3.归纳思维
学生是否具备归纳思维,关系着他们是否能够发现知识背后的规律。例如,教师引导学生思考:经过一个点,可以确定多少条直线?经过两个点,可以确定多少条直线?学生刚开始找不到答案,教师让他们应用小组合作的方式进行学习,并在实践中体验,从而找到答案。学生A认为,经过一个点能画出一条直线,学生B却应用实践的方法说明经过一个点可以画无数条直线。在探究的过程中,学生A发现自己的思维受到了限制,他在学习中要培养自己的想象力。结合教师的问题,学生A开始探索,他发现经过两个点能够确定一条直线。那么经过三个点、四个点呢?此时,学生发现只有三个点落在同一条直线上才能确定一条直线,如果三个点不在同一条直线上,那么可以确定三条直线。同理,只有四个点落在同一条直线上才能确定一条直线。如果四个点不在同一条直线上,那么可以确定六条直线。在教师的引导下,学生用举例子的方法,看到了点数与最多直线数的关联。接下来,教师指引学生思考:点数和确定的直线数是否存在规律?你们如何发现其中的规律呢?教师让学生建立表格,统计点数和确定最多直线数的规律。学生发现,不同的两个点可以确定一条直线;不同的三个点可以确定三條直线;不同的四个点最多可以确定六条直线……不同的n个点,最多可以确定n(n-1)/2条直线。通过这一次的学习,学生意识到了他们要应用归纳思维来总结发现知识的规律。
四、应用“点线”练习题,让学生发现思维盲点
由于学生的思维水平会受到外界的限制,因此他们的思维会存在一些盲点,这些思维盲点会让学生出现认知错误。教师在教学中,要结合自己的教学实践预设学生的思维盲点。如教师引导学生通过发现思维盲点了解自身存在的问题,然后在消除学习盲点的过程中提高学生的思维水平。教师在应用习题引导学生发现思维盲点时,要注意学生的个体差异性。
以此题为例:线段AB=5cm,BC=4cm,那么AC两点间的距离是(A. 1cm ;B. 13cm;C. 1cm或9cm;D. 以上答案都不对)。对于四年级的学生来说,例题的内容较为抽象,因此学生要学会绘制图形,应用发散思维来分析问题,以此找到图形绘制的多种可能性。对于学困生,这一道题过于复杂,教师可以允许学困生不完成这道题。对于中等生,教师要通过这道题培养这个阶段学生的发散思维,促其有效理解本题所涵盖的知识。而对于学优生,他们完全可以独立完成这一题。当然,教师要利用这道题,让学优生把点与线的学习和三角形的几何知识结合起来,让他们从点与线的学习,拓展到点线面的学习上。在教师的引导下,学生得出正确答案:如果A、B、C在同一直线上,当C在线段AB上时,AC=5-4=1,当C在线段AB外时,AC=5+4=9;如果A、B、C不在同一条直线上,则A、B、C构成三角形,根据三角形第三边大于两边之差,小于两边之和,最终得出1。
总之,教师在四年级“线与角”的教学中,要积极培养学生的空间思维,使学生能够应用空间概念来理解点线等相关概念,避免学生把生活中的概念与数学几何概念相混淆;还要引导学生应用抽象思维分析问题,使学生能够理解每一个概念的异同,并初步建立数学概念体系,为学生寻找数学规律打好基础。教师在引导学生探寻点线之间的规律教学时,要培养学生的发散思维、分类思维、归纳思维,学生只有具备发散思维,才能在探寻的时候找到问题的答案;教师引导学生应用分类思维来分析问题,可以让学生把知识条理化,为学生找寻知识规律打好基础;教师引导学生应用归纳思维来分析问题,可以让学生以探寻的结果为基础,找到知识的规律。即使学生找到了具体的学习方法,他们的思维还是会存在盲点,此时教师就要引导学生消除盲点,让他们利用所学知识解决相关数学问题。
作者单位 陕西省西安市城南中学
