求解平面向量问题的三个小措施

徐峰 陆晓芳

平面向量兼有“数”与“形”的双重属性.在解答平面向量问题时，可以从“数”与“形”两个角度入手，来寻找不同的解题思路.下面结合实例，探讨一下求解平面向量问题的三个小措施.

一、采用基底法

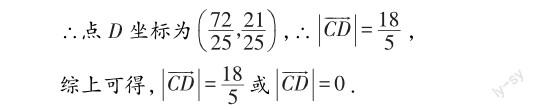
由于∠BAC=90°，所以可以点A为原点，AB所在的直线为x轴，建立平面直角坐标系，将相关的点用坐标表示出来，即可通过向量的坐标运算，求得D点的坐标以及CD的长度.

三、利用平面几何图形的性质

在解答平面向量问题时，我们经常需结合图形来解题，这就需要用到平面几何图形的性质，如长方形、平行四边形、等边三角形、圆的性质，据此建立关系式，求得问题的答案.在利用平面几何图形的性质解题时，往往要将图形中的线段看作向量的模，将线段之间的夹角看作向量之间的夹角或其补角.

相比較而言，基底法、坐标法比较常用，几何性质法较为灵活.无论运用哪种方法解答平面向量问题，我们都需要将数形结合起来，运用数形结合思想来辅助解题，这样有利于提升解题的效率.

（作者单位：江苏省南通市海门四甲中学）