多面函数法拟合GPS高程及其程序实现

黄书华

(1.成都市勘察测绘研究院，四川 成都 610081； 2.四川省城市信息化测绘工程技术研究中心，四川 成都 610081)

1 引 言

多面函数拟合法最早由美国Hardy教授于1971年提出[1]，其基本思想是任何一个圆滑的数学表面总可以用一系列有规则的数学表面的总和以任意精度逼近。1977年美国将此法应用于大地测量、拟合重力异常、求大地水准面差距、计算垂线偏差等研究工作，1978年又将此法用于地壳形变分析[2]。随着研究的不断深入，国内很多学者也开始了相关研究并将该方法应用到了其他相关领域[3～7]。随着GPS以及我国北斗卫星系统的不断完善，卫星定位技术引发了平面定位改革，实现了平面位置的高效、高精度测定。但是使用卫星定位技术测得的大地高(H)并不能取代各类工程建设所需的正常高(h)，正常高的获取仍然需采用费时、费力的古老水准测量方法获得。如何将大地高转换为正常高，很多测绘工作者对此做了大量研究。其中一种行之有效的方法就是通过测量均匀分布点位的大地高和正常高，由公式ξ=H-h求得这些点位的高程异常值，然后通过数学模型拟合其他未知点的高程异常值，再结合这些未知点的大地高求得需要的正常高。由于精度有限，目前此法一般只能达到四等水准测量的精度要求[8，9]，但这仍然可以避免许多繁重的外业水准测量工作。

本文首先结合GPS高程拟合介绍了多面函数拟合的原理及方法，然后通过具体的实例，结合自己编制的应用程序，对比分析了不同核函数及光滑因子对多面函数GPS高程拟合结果的影响。

2 多面函数拟合GPS高程原理及方法

多面函数的一般形式可表示为：

(1)

其中：αj为待求参数，Q(x，y，xj，yj)是核函数，n为核函数的个数。核函数Q(x，y，xj，yj)是关于x、y的二次函数，其中(xj，yj)为已知点坐标。使用多面函数拟合法两个最重要的问题是核函数和光滑因子的选取，从理论上来说任何核函数只要其解唯一都可以应用[2]，但是在实际应用中发现对于具体的模型，核函数选取是否合理对多面函数的拟合效果有较大的影响；另一个影响多面函数拟合效果的因素是核函数中光滑因子的选取，文献[9]建议光滑因子宜选取一小正数或零，而马洪滨等提出了一种距离相关的光滑因子求解方法，即认为光滑因子宜取已知点集合与未知点集合中距离最远两点的距离值[10]。常用的核函数有以下3种类型：

正双曲面函数：

Q(x，y，xj，yj)=[(x-xj)2+(y-yj)2+δ]1/2

(2)

反双曲面函数：

Q(x，y，xj，yj)=[(x-xj)2+(y-yj)2+δ]-1/2

(3)

三次曲面函数：

Q(x，y，xj，yj)=[(x-xj)2+(y-yj)2+δ]3/2

(4)

以上三式中δ即为光滑因子，起到调节核函数大小的作用。

采用GPS测量所获得的高程坐标是在WGS-84椭球下的大地高，然而我国采用的是正常高系统[8]，因此由GPS测得的大地高并不能直接应用于工程实践中，然而两者之间存在如下转换公式：

h=H-ξ

(5)

其中h表示正常高，H表示大地高，ξ表示高程异常。若想由大地高求得每个待求点的正常高，就必须知道该点对应的ξ值，实际情况下是不可能实地测量每一点的ξ值。实际生产中的做法是在测区选取一定数量均匀分布的水准重合点，采用GPS测量获得这些点大地高的同时，对这些点进行相应精度的水准测量得到正常高，这样就可以求得这些点的高程异常值。利用这些公共点的ξ值，可以采用拟合的方法求得其他未知点的高程异常值。

假设有m个公共点，选择其中n(m≥n)个均匀分布的公共点作为核函数的中心点，利用以求得公共点的ξ值，可以构造如下方程式：

(6)

写成矩阵形式可表示为：

(7)

至此，可以采用最小二乘法求得上式中的待求参数X：

X=(ATA)-1(ATy)

(8)

对于其他只有大地高(H)的点，同样可以够造核函数矩阵，利用求得的参数值求出这些点对应的高程异常值ξ，利用式(5)就可以求出这些点的正常高h。

3 实例程序分析

由上述分析可知，采用多面函数法拟合GPS高程的关键是核函数及光滑因子的选取，在这两者确立了之后，可采用联测的公共点构造形如式(6)的方程式求得参数值，进而求取未知点的高程异常值ξ。为了更全面的分析核函数及光滑因子对拟合效果的影响，采用C#语言编制了多面函数法拟合GPS高程的程序，其界面如图1所示。

该程序可手动输入已知点、待拟合点数据，也可以自通过文件形式读入。中心点即可以通过文件的形式读入，也可以在已有的已知点列表中选择。在数据准备好之后，可选择相应的核函数并输入光滑因子，点击“计算”按钮可实现自动拟合计算，结果将增加到待拟合点列表之后。为了验证采用多面函数法拟合GPS高程的可行性以及自编程序的高效性，现采用一组工程实测数据进行验证，这些点都进行了GPS测量及水准数据，数据如表1所示。

图1 多面函数法拟合GPS高程程序界面

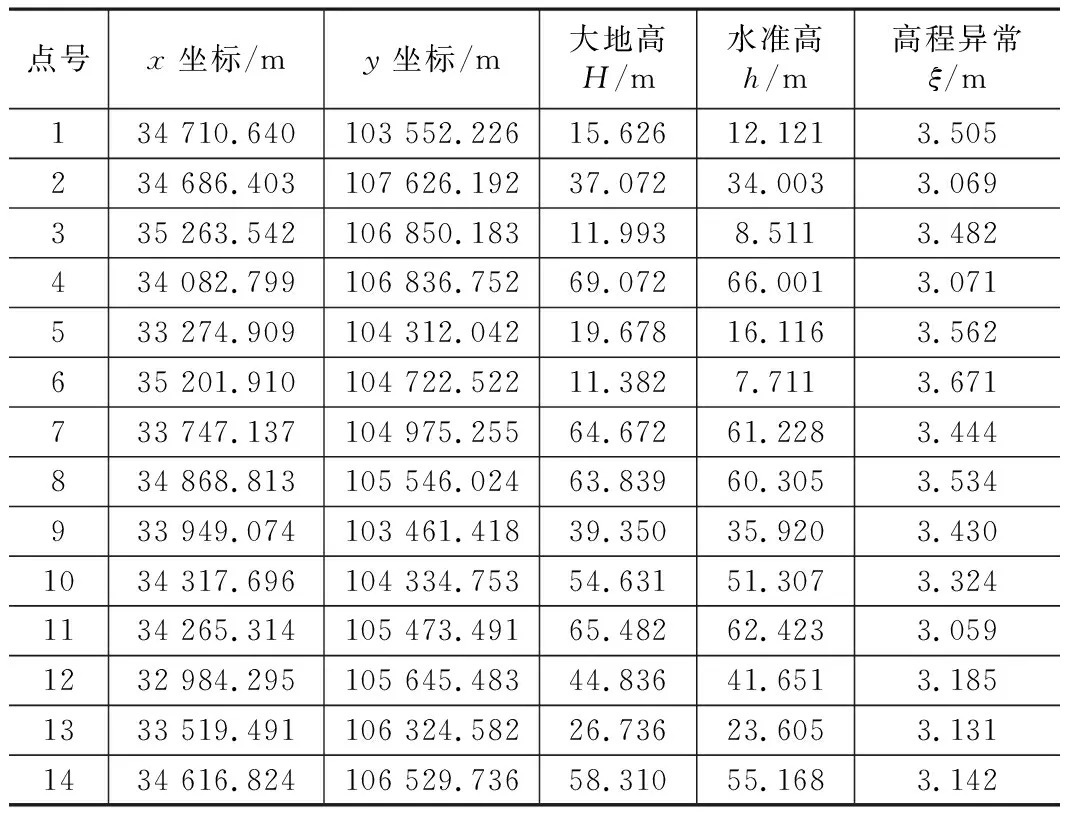
GPS测量及水准测量数据 表1

选取其中均匀分布的7个点作为已知点，剩下的7个点作为待拟合点进行检验。由于已知点是在所有点位中均匀选取的，可将其全部作为中心点进行参数的求解，具体的点位选择及分布如图2所示。

图2 中心点及待拟合点分布示意图

应用编制的程序可采用不同的核函数、不同的光滑因子，对实例数据进行拟合。在本例应用中选择某一核函数后，不断调整光滑因子的值，总体情况来看选择正双曲面函数时拟合效果最佳，三次曲面函数次之，反双曲面函数结果最差。在确定使用正双曲面函数作为核函数之后，光滑因子取不同值对拟合结果影响如表2所示。

不同光滑因子值对正双曲面函数拟合影响 表2

注：δ=3062是文献[10]方法计算的已知点集合与未知点集合中距离最大的数值。

从拟合效果来看，选取δ=0时效果最佳，随着δ的不断增大，每个点的拟合效果都呈现出一定的趋势，其中3、4、5、13、14呈减小趋势，而6、10呈增大趋势。本算例中结果与文献[9]建议取δ=0相符，拟合值与实测值相比在mm级，可满足四等水准测量的要求。虽然在本例中取δ=0效果最佳，但是并不能得出一般性的结论，在使用该程序验证其他文献的实例时，并不是每次光滑因子取零都能获得最佳拟合效果，如文献[10]中建议取已知点集合与未知点集合中距离最大的值。建议在采用多面函数法进行GPS高程拟合时，先通过比较几种常用的核函数确定出适合的核函数，而后不断调整光滑因子，直到两者匹配达到最好的拟合效果。

4 结 论

(1)GPS测量技术的快速发展带来了平面位置测量方式的改革，想要充分利用GPS测量技术获得的大地高，可利用多面函数拟合法等将其转化为生产实践需要的正常高，可代替外业四等水准测量，从而降低生产成本；

(2)在采用多面函数法拟合GPS高程时，已知点及中心点的选取至关重要，选取均匀分布的已知点及中心点有利于提高拟合精度；

(3)在选择光滑因子之前，宜先确定一个适合的核函数。在GPS高程拟合时，结合本文及相关文献结论，核函数应采用正双曲面函数。对于光滑因子的选取，应该在核函数确定后进行不断调整试算，以期达到最佳拟合效果。