最佳自适应无迹卡尔曼滤波算法应用研究

曹后龙

(上海核工程研究设计院有限公司，上海 200233)

1 引 言

在卡尔曼滤波应用中，状态方程或量测方程常为非线性函数，则滤波问题也表现为非线性，为了解决在非线性系统中卡尔曼滤波理论的应用问题，S.J.Julier和J.K.Uhlmann提出了无迹卡尔曼滤波[1，2，3]，该算法采用线性卡尔曼滤波框架，以无迹变换为基础，通过某种采样策略生成采样点集，然后将采样点集通过无迹变换得到新的采样点集，将变换后采样点集的统计特性作为问题结果，避免了线性化误差，而且需要很少的采样点就可以得到优于扩展卡尔曼滤波的估计结果，不仅易于实现而且在保持与线性化方法相当运算量的同时具有较高的估计精度和较广的适用范围[4]。

在许多实际问题中，无迹卡尔曼滤波对前一时刻状态参数估值比较敏感，其误差将会直接影响滤波的估值；即使前一时刻状态参数估值合理，由于动力学模型异常误差的存在，这也会直接影响无迹卡尔曼滤波滤波解的精度[5]。针对上述问题，恰当的自适应因子不仅能够合理地平衡预测状态信息与观测信息之间对滤波估值的贡献，而且能够很好地控制前一时刻状态参数估值误差与动力学模型异常误差对滤波估值的影响[6，7，8]。

本文在自适应无迹卡尔曼滤波算法的理论基础上，给出了其改进算法，引入最佳自适应因子[9]，得到最佳自适应无迹卡尔曼滤波。通过最佳自适应因子来调节预测状态向量的协方差矩阵，即调整预测状态信息对滤波解更加合理的贡献，从而进一步提高滤波解的精度。

2 自适应无迹卡尔曼滤波算法

已知tk时刻的状态方程和观测方程分别为：

Xk=Φk，k-1Xk-1+wk

(1)

Lk=h(Xk)+ek

(2)

式中，状态方程为线性函数，观测方程为非线性函数；Xk为tk时刻的n×1维状态向量，Φk，k-1为状态转移矩阵，Lk为tk时刻m×1维观测向量，h(Xk)为非线性观测函数；wk和ek分别为n×1维状态噪声向量和m×1维观测噪声向量，均为加性高斯白噪声，两者的协方差矩阵分别为Qk和Rk，且互不相关。

(3)

(4)

(5)

其协方差矩阵和估值为：

(6)

(7)

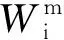
(8)

(9)

(10)

(11)

3 最佳自适应因子

在自适应无迹卡尔曼滤波中，恰当的自适应因子不仅能够合理地平衡预测状态信息与观测信息之间对滤波估值的贡献，而且能够很好地控制前一时刻状态参数估值异常误差与动力学模型异常误差对滤波估值的影响。

(12)

(13)

(14)

(15)

(16)

则：

(17)

对上式两端同时取迹可得Ck为：

(18)

(19)

4 算例及分析

在教学楼前广场进行动态导航定位实验，车辆载体安装导航模块，实验时长 20 min，接收机采样间隔T=10s。利用接收机自带的处理软件从原始数据文件里导出观测文件和广播星历文件，并对观测数据和导航数据进行简单的处理，取观测数据次数100次。动力学模型采用常速(CV)模型[12，13]，观测模型采用伪距观测方程[14]。

初始状态参数估计值X0及其协方差矩阵D0为：

D0=diag(100，100，100，100，0.0012，0.0012，0.0012，1)

状态噪声协方差矩阵Q和观测噪声协方差矩阵R为：

Q=diag(100，100，100，100，0.0012，0.0012，0.0012，1)

R=diag(100，100，100，100，100，100，100)

使用标准无迹卡尔曼滤波算法和最佳自适应无迹卡尔曼滤波算法分别进行滤波计算比较分析，采样策略为对称采样。

(1)状预测态信息无异常误差时，即动力学模型无异常误差，前一时刻状态参数估值无异常误差，如图1～图3所示。

图1 预测状态信息无异常误差时，X坐标差值比较

图2 预测状态信息无异常误差时，Y坐标差值比较

图3 预测状态信息无异常误差时，Z坐标差值比较

(2)在给定初始状态估值X0不恰当时，即初始状态参数估值存在较大误差时，x、y、z坐标差值如图4～图6所示。

X0=[-2412100.0 4687600.0 3564900.0 609729.1 0 0 0 100.0]T

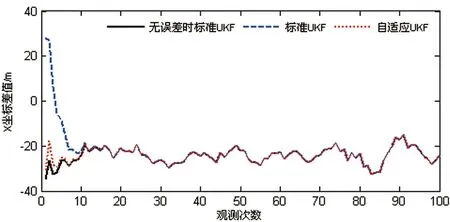
图4 初始状态估值有误差时，X坐标差值比较

图5 初始状态估值有误差时，Y坐标差值比较

图6 初始状态估值有误差时，Z坐标差值比较

(3)为了检验最佳自适应因子的效果，每隔20次就在前一时刻状态参数估值向量中的X坐标，Y坐标和Z坐标上分别人为地加上 80 m异常误差，x、y、z坐标差值如图7～图9所示，即：

图7 前一时刻状态估值有异常误差时，X坐标差值比较

图8 前一时刻状态估值有异常误差时，Y坐标差值比较

图9 前一时刻状态估值有异常误差时，Z坐标差值比较

(1)从图1、图2、图3可以看出，在观测值可靠的情况下，在滤波初始段，标准无迹卡尔曼滤波估值精度稍微低于最佳自适应无迹卡尔曼滤波估值精度；但在标准无迹卡尔曼滤波算法稳定以后，两者的滤波结果基本一致，精度相当。

(2)从图4、图5、图6可以看出，在观测值可靠的情况下，由于状态参数初始值存在较大误差，导致了标准无迹卡尔曼滤波初期的滤波结果发散，精度很差，但随着滤波的进行，逐渐趋于稳定；而最佳自适应无迹卡尔曼滤波通过最佳自适应因子调整初始状态估值的协方差矩阵，减少初始状态估值对滤波解的贡献，得到了可靠的滤波结果，提高了滤波估值的精度。

(3)从图7、图8、图9可以看出，在预测状态向量存在较大误差时，标准无迹卡尔曼滤波稳定性很差，得到的滤波结果不可靠；而此时最佳自适应无迹卡尔曼滤波能够很好地控制预测状态信息对滤波结果的影响，得到可靠的滤波结果。

5 结 论

本文先给出了自适应无迹卡尔曼滤波算法，再利用预测残差的理论协方差矩阵与实际协方差矩阵之间的关系，引入无迹卡尔曼滤波中最佳自适应因子，得到了最佳自适应因子无迹卡尔曼滤波算法。当预测残差实际协方差和理论协方差相等时，即自适应因子Ck=1，此时的自适应无迹卡尔曼滤波就是标准无迹卡尔曼滤波。在观测值可靠的情况下，预测残差反映了动力学模型误差与前一时刻状态估值误差总共的大小，最佳自适应无迹卡尔曼滤波将它们作为一个整体，利用最佳自适应因子合理地调整它们整体对滤波结果的贡献。通过实例验证了最佳自适应因子在无迹卡尔曼滤波中不仅能够适用，而且能够提高滤波结果的精度。