基于记忆策略的动态分解约束多目标进化算法

陈创明，温洁嫦

（广东工业大学应用数学学院，广东 广州 510520）

0 引言

约束多目标优化问题广泛存在于科学、工程、医学等众多领域中[1-4].一般情况下，约束多目标优化问题可以表述为：

其中D是n维自变量空间，F（x）是m维目标函数向量，同时满足所有的约束条件gi（x）和hi（x）的自变量的取值范围即为容许域.在容许域中的解称为容许解，反之称为非容许解.gi（x）是第i个不等式约束条件，hi（x）是第i个等式约束条件.

在实际优化问题[5-7]中，约束的存在不仅使可行域变小，同时还使得整个进化过程变得更加复杂.这要求一个算法在解决多目标优化问题需要具有高效的约束处理方法.文献[8]提出了2种基于分解的约束多目标进化算法，即CMOEA/D-CDP和CMOEA/D-SR，这两个算法都偏重于选择容许解.当遇到一个带严重约束的多目标优化问题时，特别是当这个问题的容许域是分开的几片时，它们有可能会陷入其中一个片容许域中，而很难跳到另外一片容许域中，除非它们靠的很近.文献[9]提出了一种基于引导权重的约束多目标进化算法，该方法通过一组非容许权重保持非容许解的散布性，从而为算法的寻优提供有效的帮助.近年来，在进化过程中短暂忽略约束的约束处理方法引起了众多学者的关注[10-13].这类方法在处理约束时不考虑约束，从而避免进化过程约束所带来的求解困难，接着在某个阶段开始考虑约束，并逐渐收敛到可行域中.该方法在求解约束多目标优化问题中具体明显的优势，但是，当不考虑约束的最优解边界与考虑约束的最优解边界不一致时，这类方法难以收敛大部分考虑约束的最优解边界上.因此，如何有效地收敛到容许域，进而寻找最优解成为这类方法的痛点.

近10年来，基于分解的多目标进化算法得到了充分的发展，在多目标优化领域上取得了大量的成果[14-17].其中，文献[15]提出一种具有区域保护机制的分解多目标进化算法（M2M）.该方法将一个多目标优化问题分解成多个简单子多目标优化问题.该方法被设计用于求解无约束的多目标优化问题.对于约束多目标优化问题，该方法的某些子问题由于约束的原因可能只保留了非容许解或者为空集，浪费了计算资源，导致算法的求解效率低下.

针对上述问题，本文首先在基于短暂忽略约束的约束处理方法基础上，引入具有记忆功能的归档集，将进化过程中的容许解保留下来，并用于指导算法进入容许域，避开陷入非容许域中，从而提高算法的求解鲁棒性.接着，提出一种动态分配计算资源的分解策略，对于具有全是非容许解或者为空集的子问题的计算资源重新分配到其他子问题中，从而提高算法的求解性能.

1 基于记忆与动态分解策略的算法设计

1.1 基于记忆策略的约束处理方法

基于短暂忽略约束的约束处理方法在求解约束多目标优化问题具有优秀的性能，但对于非容许与容许最优界面不一致的问题，求解效果较差.针对这种情况，本文采用基于两阶段策略与具有记忆功能的归档集保存历史发现的容许解，在第一阶段跳转到第二阶段时将保存在归档集中的容许解用于指导算法进入容许域，同时保留当前较优的非容许解于归档集中，用于后续算法寻优.具体步骤如算法1.

算法1：基于记忆策略的约束处理方法1）每10代判断跳转条件：使用式子（2）衡量第1代与第10代之间的相似度，当IGD值小于预先给定的值r时，则跳转到第二阶段.否则保留在第一阶段.2）第一阶段：在第一阶段中，在评价个体间的优劣时只通过目标值的非支配关系进行对比，并将容许解保存到归档集A中，当A的大小超过种群大小N时，则使用非支配排序选择前N个最优个体.3）第二阶段：进入第二阶段时，首先将归档集中的容许解参与种群选择操作，替代非容许解，同时将非容许解中的非支配解保存到归档集，并参与后续进化过程，提高求解的质量.在该阶段中使用基于容许解优先的约束处理方法进行选择个体.

本文使用IGD度量[18]衡量两个种群的相似度，当IGD值越小时，其两个种群越相似.一般情况下，IGD度量用于衡量一个多目标进化算法的收敛性能，由式（2）给出：

其中，P*与P是给定的2个种群，d（v，P）表示个体v到种群P的距离.

在第二阶段中，个体依照基于容许解优先的约束处理方法进行选择个体，具体步骤如下：

1）当容许解个数大于N时，从中按非支配排序选择前N个容许解作为下一代种群个体.

2）当容许解个体小于N时，则优先选择全部容许解，剩下的个数从非容许解中按约束违反程度从小到大选择，直到种群大小为N.

1.2 动态分解策略

文献[15]提出的M2M算法是一种具有区域保护机制的分解多目标进化算法.M2M将问题（1）分解成S个简单的多目标优化子问题，并在一次运行中同时解决这个S个子问题.该算法首先从目标空间上的超平面上均匀取S个单位中心权重向量v1，…，vs，接着将目标空间分成S个子区域Ω1，…，Ω2，其中，Ωi由式（3）表示：

j＝1，2，3，…，S，〈F（x），vj〉是 F（x）和 vj之间的夹角.

该算法将靠近于某一单位中心权重向量的个体规划为同一个区域，对于约束多目标优化问题，某个区域可能全是非容许解或者这个单位中心权重向量周围没有个体而导致这个子区域不存在个体.当M2M遇到某子区域没有个体时，并从种群中随机复制其他个体.但是这种做法并不能提升算法的性能，个体的重复复制占用算法的计算资源.针对上述情况，本文提出一种动态分配计算资源的分解策略，具体思想如算法2.

算法2：基于动态分配计算资源的分解策略1）每隔k代判断S个子区域中分配情况：当算法进入第二阶段后，每隔10代判断S个子区域的个体分配情况.2）当第i个子区域中存在全部个体为非容许个体或者为空：将该子区域的计算资源随机分配其他子区域中，即随机增加其他子区域的大小，而该区域不再用于选择个体，保持种群的大小始终为N.

由于第一阶段处于搜索的过程，最大程度保留分区域的机制，有利于算法寻找出最优解区域，因而在这个阶段中不采用该动态分解策略.当算法进入到第二阶段时，每隔k代判断每个子区域是否存在全是非容许解或者空的情况.若是，则将该子区域的选择个体次数随机分配到其他子区域中，提升算法对计算资源的利用率.值得注意的是，对于存在全是非容许解或者空集的子区域，依然保留着单位中心权重向量，当该子区域在某一代中被分配到容许个体时，则重新用于选择下一代个体.

1.3 本文算法流程

结合章节2.1和2.2，本小节提出本文的算法框架.基于记忆策略的动态分解约束多目标进化算法的具体步骤如下：

1）参数设置及初始化.产生一个大小为N初始种群，在m维超平面上均匀产生N个权

2）重向量以及S个单位中心权重向量.初始化M2M算法的参数，包括子区域的种群大小si，参考点.设置算法停止条件.

3）根据式（1）和式（5）计算种群的目标函数值 F（x）和约束违反程度 G（x）.

4）使用基于DE/RAND/1/BIN[5]的进化算子产生子代种群.

5）将父代种群与子代种群合并到一起，根据式（3）进行分区域，并更新M2M的参数.

6）根据算法1和算法2，将步骤4中分区域后每一个子种群进行选择操作，选择si个最优个体进入到下一代.

7）判断是否满足算法停止条件.如是，停止算法，并输出当前种群的容许个体作为求解的约束多目标优化问题的最优解集.否则跳转到步骤3.

根据式（1），个体x在第i个约束的约束违反程度使用式（4）进行计算：

然后，个体x的违反约束程度由式（5）给出：

其中，δ是容忍因子，通常取值0.000 1.

2 实验结果及分析

2.1 对比算法与基准测试问题

本文算法与CMOEA/D-CDP[2]以及CM2M2[8]进行算法对比（见表1），两者都采用基于分解的多目标进化算法.CMOEA/D-CDP采用基于容许解优先的约束处理方法，而CM2M2使用一组非容许权重保持优秀的非容许解的散布性，从而达到更好地利用非容许解，为算法提供更好的进化方向.

表1 本文提出的算法与CMOEA/D-CDP、CM2M2的实验对比结果

本文采用CTP系列约束多目标优化问题[8]作为基准测试问题，并使用1个实际工程优化问题Speed Reducer Design Problem（SRDP）[19]进一步检验本文提出算法的性能，该问题包括2个目标函数，7个决策变量，和11个不等式约束.

2.2 评价指标

本文采用IGD和HV[20]度量指标评价约束多目标进化算法的性能.其中，IGD度量指标用于衡量求到的种群与真实最优边界的相似度，IGD值越小，算法的收敛性能越好.而HV用于同时衡量算法的收敛性与散布性，HV值越大，说明算法的收敛性与散布性更好.在计算HV值时，需要事先给定一个参考点.在本文中，CTP1-CTP8的参考点设置为真实最优边界，每一个目标维度的最大值的1.1倍，SRDP的参考点设置为（3，18）.

2.3 算法参数设置

本文提出的算法与对比算法的参数设置如下：

1）种群大小N设置为100，运行代数设置为1 000代.

3）用于衡量两个种群相似度的参数r设置为0.005；所隔代数k设置为10.

4）基于DE/RAND/1/BIN的进化算子的DE参数CR设置为0.1，F设置为0.8.

5）本文提出的算法和对比算法在9个测试问题上分别独立运行30次.

6）CM2M2的非容许权重数设置为30，容许权重数设置70.

7）CMOEA/D-CDP与CM2M2剩下的参数与原文保持一致.

2.4 实验结果与分析

表1展示了本文所出算法与CMOEA/D-CDP、CM2M2基于IGD与HV度量指标的平均值与标准差的实验对比结果.算法在某一个测试问题求到的结果最优则进行标黑处理.

从表1的结果观察可以得出，本文所提出的算法在大部分基准测试问题如CTP1、CTP2、CTP6、CTP8以及SRDP上相比于CMOEA/D-CDP与CM2M2求到更优的结果，说明了本文所提算法在这些问题上求到解集的收敛性与散布性更优.而且在CTP3、CTP5与CTP7求到的HV值也优于另外两个对比算法，进一步证明了本文所提算法性能的优异性.由于CTP6与CTP8具有约束难的特点，特别是CTP8，具有几片离散容许域，导致CMOEA/D-CDP陷入了局部最优区域中，主要是由于该算法使用了基于容许解优先的约束处理方法.对于CM2M2，在CTP6与CTP8都求到了最优边界，但在这2个测试问题上CM2M2的部分子区域保留的个体全是非容许的或者为空，浪费了计算资源.由于CM2M2与本文的算法都采用同一种分区域策略，因此CM2M2在CTP6与CTP8的实验结果从侧面验证了本文所提出的基于动态分解的策略的性能.

图1-6展示了三个算法基于IGD值中位数运行的IGD变化曲线.横坐标generation表示代数，纵坐标表示IGD值，当IGD值为0时表示此时算法的种群全为非容许解.

本文所提出算法的性能可以从图1-6中直接观察得出.基于记忆功能的动态分解约束多目标进化算法优于另外两个对比算法.对于图3与图5，由于CMOEA/D-CDP陷入了局部最优区域中，导致算法最终得到较大的IGD值.同时从图3中可以观察到，当代数generation达到100时，本文所提出的算法得到的IGD值为零，主要由于此时算法位于第一阶段，在进行选择操作时忽略了约束，从而导致种群全为非容许解，随着代数的增加，算法进入了第二阶段，算法逐渐收敛于最优边界.

关于图6，算法CM2M2以及CMOEA/D只收敛到最优边界的一部分，导致最终得到较差的IGD值.另外，由于SRDP问题的最优边界具有不规则的形状，CM2M2出现了不断震荡的现象，在进化的过程，当出现少数点在不规则最优边界部分时，IGD的值则变小.但这部分的个体难以保留，因而IGD的值变大.同样的情况可以在本文算法上观察到，但由于本文算法采用动态分解的策略，从而避免该情况恶化的发生.

图1 CTP1的IGD变化曲线

图2 CTP2的IGD变化曲线

图3 CTP6的IGD变化曲线

图4 CTP7的IGD变化曲线

图5 CTP8的IGD变化曲线

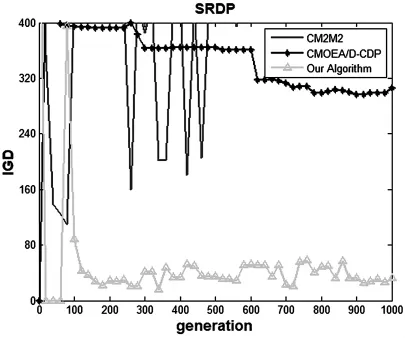
图6 SRDP的IGD变化曲线

2.5 算法参数r的敏感性分析

本小节讨论本文所提出算法中参数r的敏感度.以CTP6作为测试例子，分别取五个不同的值，即0.001，0.005，0.01，0.05和0.1.对于每个不同的r，本文算法其他参数保持不变，并独立运行30次，统计IGD与HV值，如表2所示.

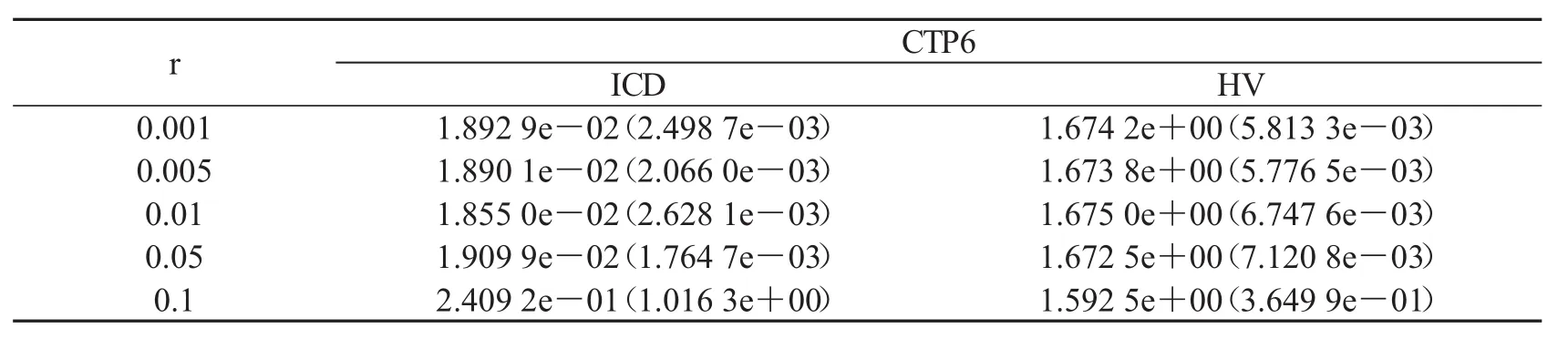
表2 参数r的敏感度

参数r用于衡量两个种群间的相似度，即控制从第一阶段跳转到第二阶段所需要的计算资源，其值越大，越容易从第一阶段跳转到第二阶段.从表2中可以看出，当参数r小于0.05时，其算法求到的IGD与HV值维持在一定的范围内，较为稳定.因为，参数r的建议取值范围为区间（0.001，0.05）.

2.6 算法参数k的敏感性分析

本小节讨论本文所提出算法中参数k的敏感度.以CTP6作为测试例子，分别取五个不同的值，即5，10，15，20和25.对于每个不同的k，本文算法其他参数保持不变，并独立运行30次，统计IGD与HV值，如表3所示.

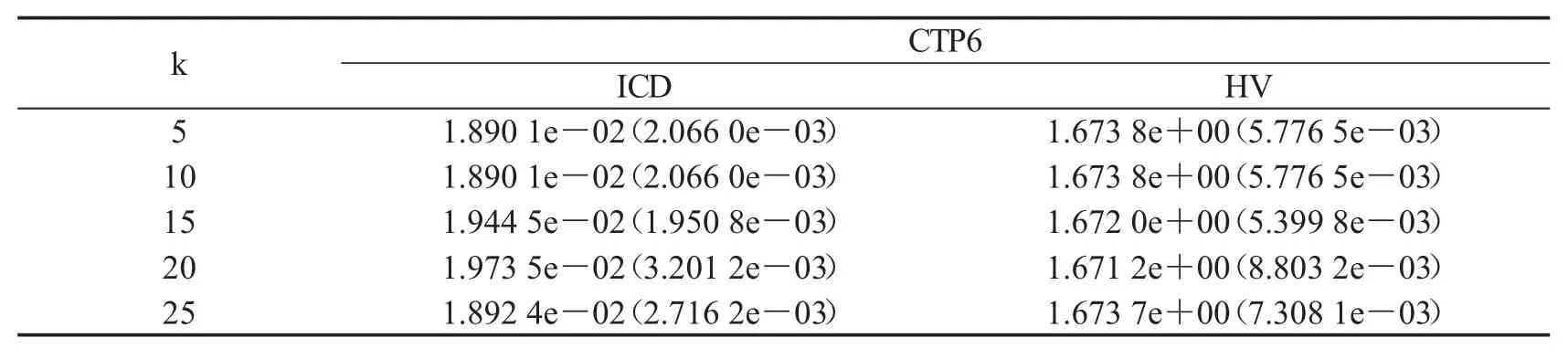
表3 参数k的敏感度

参数k用于算法进入到第二阶段时，每隔k代判断每个子区域是否存在全是非容许解或者空的情况.从表3可以看出，本文算法对该参数不敏感.

3 结论

本文提出了一种基于记忆策略的动态分解约束多目标进化算法.首先引入了具有记忆功能的归档集，改进了基于短暂忽略非容许解的约束处理方法，从而提高算法的求解鲁棒性.结合基于分解的多目标进化算法，设计了一种动态分配搜索资源的策略，提高算法的寻优能力.并将设计的算法用于求解约束多目标基准测试集和1个工程问题，仿真结果表明了本文所提出算法的优异性能.另外，本文还对所提算法进行了参数敏感度分析，结果表明该算法对参数r在取值区间（0.001，0.05）之间不敏感，对参数k在取值5～20之间不敏感.