考虑灰色关联权重的PSO-LSSVM输电线路覆冰厚度预测模型
2022-03-05郭开春
郭开春,王 波
(1.三峡大学 电气与新能源学院,湖北宜昌 443000;2.武汉大学 电气与自动化学院,武汉 430072)
引言
为了满足人们日益增长的用电需求,我国电网正朝着“特高压、远距离、大容量”的方向发展[1]。我国幅员辽阔、地理条件复杂,架空输电线路不可避免地会经过重覆冰地区[2]。输电线路覆冰会引起闪络、舞动、断线、倒塔等事故,严重时可能引发大面积停电,威胁电力系统的安全稳定运行[3]。因此,开展输电线路覆冰厚度预测研究对于减少线路遭受覆冰灾害,提高电力系统稳定性具有重要意义。
随着人们对输电线路覆冰问题的重视,大量覆冰预测方法被提出。文献[4]将主成分分析(PCA)、遗传算法(GA)与最小二乘支持向量机(LSSVM)相结合,建立了基于PCA-GA-LSSVM 的输电线路覆冰负荷在线预测模型。文献[5]在建立覆冰预测模型时考虑了气象因素和时间累积效应的共同影响,建立了相应的输电线路覆冰厚度预测模型,对实际运行的输电线路覆冰厚度进行了预测。文献[6]考虑了历史覆冰数据的影响,采用变分模态分解(VMD)历史覆冰数据,得到不同频率的分量,利用灰狼算法(IGWO)对LSSVM 进行优化,建立了基于VMD-IGWO-LSSVM 的覆冰预测模型。上述模型虽然都能较准确地预测输电线路覆冰厚度,但都没有考虑各影响因素的权重。
针对现有输电线路覆冰预测方法上存在的不足,利用灰色关联分析确定覆冰影响因素对输电线路覆冰增长量的影响权重,采用PSO 算法优化LSSVM 的参数,建立了考虑灰色关联权重的PSO-LSSVM 输电线路覆冰厚度预测模型。采用实际运行的线路覆冰数据验证模型的正确性和实用性。
1 算法介绍
1.1 灰色关联分析
灰色关联分析[7]是对某一系统发展态势进行定量描述和比较的方法,其基本思想是根据系统内数据列之间的几何形状相似度确定它们之间联系的紧密程度,即曲线之间的关联程度,简称灰色关联度。本研究采用灰色关联分析法分析输电线中覆冰厚度影响因素,其基本步骤如下。
(1)确定分析数列
根据分析目标,确定输电线路覆冰厚度为参考序列,设为y(k),k= 1,2…n,n为样本容量,覆冰影响因素为比较序列,设为xi={xi(k)|k= 1,2…m},m为特征量的个数。
(2)数据归一化
参考序列和比较序列的数量级和单位通常不同,为了便于分析,需要对各序列归一化处理,公式如式(1)所示。

式中:xi为某一特征量的原始值;ximax和ximin分别为某一特征量的最大值和最小值;xi′为某一特征量归一化后的数值。
(3)计算关联系数
关联系数指比较序列与参考序列在各时刻的关联程度,y(k)与xi(k)在第k时刻的关联系数ξi(k)为:

式 中:ρ为 分 辨 系 数,ρ∈(0,1),通 常 取ρ= 0.5,miinmkin|y(k) -xi(k)|为所有比较序列与参考序列绝对差值的最小值,maixmkax|y(k) -xi(k)|为所有比较序列与参考序列绝对差值的最大值。ξ∈(0,1),当ξi(k) <0.5 时,表示关联性较弱;当0.5 ≤ξi(k) <0.7 时,表示关联性较强;ξi(k) ≥0.7时,表示关联性很强。
(4)确定关联度
灰色关联度指比较序列与参考序列整体的关联程度,即对各时刻关联系数取平均值,其计算公式如式(3)所示。

式中:ri为灰色关联度,取值及含义同ξi(k)。
1.2 最小二乘支持向量机


式中:w∈Rk为权值向量;b∈R为阈值。
依据结构风险最小化原则,将松弛变量引入回归方程,可得目标函数及约束条件如式(5)所示。

式中:ξi为松弛变量,ξi≥0;C为惩罚因子,C>0。在式(5)中引入拉格朗日乘子,得到下列函数:

式中:αi为拉格朗日乘子,αi≥0。
上述函数取得极值时,存在下列关系:

消去式(7)中的w和ξi,得到下列线性方程组:

在式(8)中,有

令Ω =ZZT,并 引 入 核 函 数K(xi,xj)=φ(xi)T·φ(xj),则有

综合式(8)~(10),可得:

根据最小二乘法,可以得到下列回归函数:
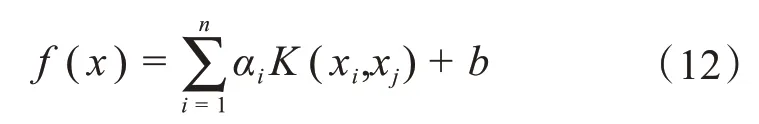
为了提高LSSVM 的泛化性能,核函数采用高斯径向基核函数,具体如下:

式中,σ为核函数参数。
惩罚因子C和核函数参数σ是LSSVM 的两个非常重要的参数,它们对LSSVM 回归拟合效果影响很大。为了获得更好的拟合效果,需要对C和σ进行寻优。
1.3 粒子群优化算法
粒子群优化算法(PSO)是由E-berhart和Kennedy 提出的一种全局寻优算法,其寻优思想是模仿群鸟捕食行为获得优化问题的最优解[9]。
PSO 寻优原理如下:设D维空间中的种群为X=(x1,x2,…,xn),该种群中有n个粒子,每个粒子均表示一个可行解,其中第i个粒子位置向量为Xi=(xi1,xi2,…,xid)T,速度向量为Vi=(vi1,vi2,…,vid)T,种群的个体极值可表示为Pi=(pi1,pi2,…,pid)T,群体极值可表示为Pg=(pg1,pg2,…,pgd)T。PSO 通过下列公式更新粒子的速度和位置:

式中:k为迭代次数;v和为x分别为第i个 粒 子在第k次迭代时的速度和位置;d= 1,2,…,D,i=1,2,…,n;ω为惯性权重;c1、c2均为加速因子,c1、c2∈(0,+ ∞);r1、r2均为随机函数,r1、r2∈[0,1]。
在PSO 算法中,惯性权重的取值能够影响粒子群的局部搜索和全局寻优能力。在迭代前期,惯性权重取值较大有利于粒子群开展局部搜索;而在迭代后期,惯性权重取值较小有利于粒子群局部寻优。为了利用迭代次数实现惯性权重的动态调节,具体如下:

式中:ωmax、ωmin分别为惯性权重的最大值和最小值;kmax为最大迭代次数。
PSO 算法原理简单、参数少,容易实现,且在寻优过程中不易陷入局部最优,目前被广泛应用于医疗、电力、交通等领域。
2 考虑灰色关联权重的PSO-LSSVM 输电线路覆冰厚度预测模型
研究表明,输电线路覆冰增长受温度、湿度、风速等多种因素的影响。各因素对线路覆冰的影响有所不同,因此在建立覆冰厚度预测模型时需要考虑各因素权重的影响。本研究将各因素与覆冰厚度的灰色关联度作为权重值,则覆冰厚度预测模型输入量与输出量的关系如下:
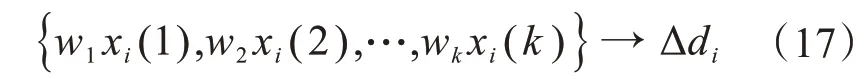

式中:wk为第k个影响因素的灰色关联度;xi(k)为第k个影响因素在i时刻的值;Δdi为i时刻覆冰厚度增长值;yi+1、yi分别为i+1时刻和i时刻的覆冰厚度。
2.1 模型的建立
考虑灰色关联权重的PSO-LSSVM 输电线路覆冰厚度预测模型的建模思路如下:首先采用灰色关联分析法计算各影响因素与覆冰厚度的灰色关联度,确定模型的输入量;然后采用训练集数据进行训练,利用PSO 算法对LSSVM 的惩罚因子C和核函数参数σ进行优化,获得C和σ的最优解,将其赋值给LSSVM 对测试集数据进行预测。具体建模步骤如下。
(1)根据灰色关联分析结果,获得更影响因素的权重,根据式(17)确定新的样本数据。将样本数据划分为训练集和测试集。
(2)初始化设置LSSVM 参数,设置C和σ的初始值分别为100 和1,给定C和σ的寻优范围,将均方根误差作为适应度函数,公式为:

式中:N为样本容量;yi为i时刻覆冰厚度实际值;yi′为i时刻覆冰厚度预测值。
(3)设置PSO 算法的相关参数,具体如下:空间维数D为2,种群规模N为30,惯性权重最大值ωmax和最小值ωmin分别为0.9和0.4,最大迭代次数kmax为200,加速因子c1、c2均为2。
(4)将C、σ作为粒子,并设置当前个体最优解为100和1,根据式(19)计算各粒子初始适应度值。
(5)开始执行迭代,每执行一次迭代,均利用公式(14)和(15)更新粒子的速度和位置,得到C和σ一组新解。
(6)将C和σ新解赋值给LSSVM,根据式(18)重新计算新适应度值。
(7)将新适应度值与当前适应度值比较,若新适应度值优于当前适应度值,则将新适应度值作为当前最优适应度值;否则,保持不变。
(8)根据迭代终止条件判断当前最优适应度是否满足要求或者算法已达到最大迭代次数,若是,则输出C和σ的最优解;否则,返回步骤(5)继续迭代。
(9)将C和σ的最优解赋值给LSSVM 完成对测试集数据的预测。
2.2 模型的评价
为综合评价模型的预测效果,本研究采用均方根误差、平均相对误差和全局最大误差进行评价。均方根误差的公式已在前文中给出,平均相对误差和全局最大误差的公式如下:

式中,M为测试集样本容量。
3 算例分析
采用西南地区某500 kV 架空输电线路覆冰监测数据进行算例分析。输电线路等值覆冰厚度[10]来源于覆冰监测装置,温度、湿度、风速、气压等数据来源于当地气象部门;本次覆冰增长时间为2016年1 月5 日22:00 至2016 年1 月7 日9:00;数据采样频率为1 h/次,共获得36 组覆冰数据。部分数据如表1所示。
对表1中覆冰增量与各气象因素进行灰色关联分析,各因素灰色关联度的计算结果如表2 所示。由表2 可知,风速、温度、湿度和气压对输电线路覆冰增长量的影响程度逐渐减弱,由于它们的灰色关联度均大于0.5,说明它们对输电线路覆冰厚度增长均有影响。
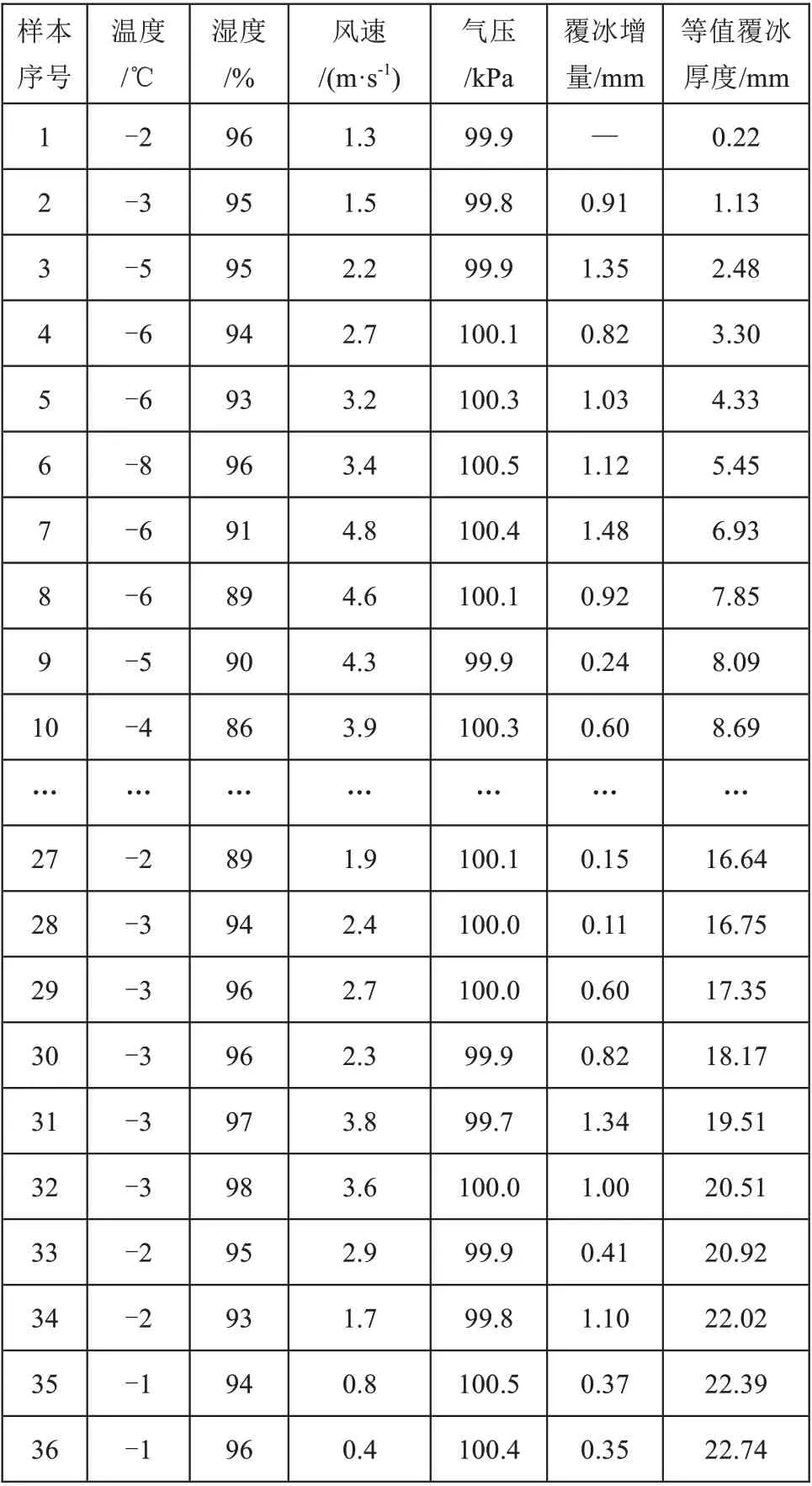
表1 部分覆冰数据

表2 灰色关联度计算结果
根据公式(17)和(18)得到新的样本数据,并将36 组数据分成训练集和测试集。其中,训练集30组,用于模型的训练;测试集6 组,用于检验模型的预测精度。利用训练集数据进行训练,建立考虑灰色关联权重的PSO-LSSVM 输电线路覆冰厚度预测模型,采用PSO 算法对LSSVM 的惩罚因子C和核函数参数σ寻优,得到C和σ的最优解分别为26.35和1.84。图1给出了LSSVM 的C和σ取最优解时模型的训练效果,为了对比考虑灰色关联权重的PSOLSSVM 模型的训练效果,图1 中同时给出了未考虑灰色关联权重的PSO-LSSVM 模型的训练效果。对比图1 中两种模型的训练效果,考虑灰色关联权重的PSO-LSSVM模型的覆冰预测值更接近实际值。

图1 两种模型训练效果图
图2 给出了两种模型的训练误差。由图2 可知,考虑灰色关联权重的PSO-LSSVM 输电线路覆冰厚度预测模型的训练误差波动性更小,训练效果更好。

图2 两种模型训练误差图
利用两种已训练好的模型预测6 组测试集数据,预测结果如图3 所示。为了进一步验证本覆冰厚度预测方法的优势,采用同样的数据,利用文献[11]和文献[12]中的覆冰预测方法,分别建立PSOEM-LSSVM 覆冰厚度预测模型和AMPSO-BP 预测模型,对测试集数据进行预测,预测结果也展示在图3 中。由图3 可知,虽然AMPSO-BP 模型个别数据预测效果好于本文模型,但从整体上看,本研究预测效果更好。
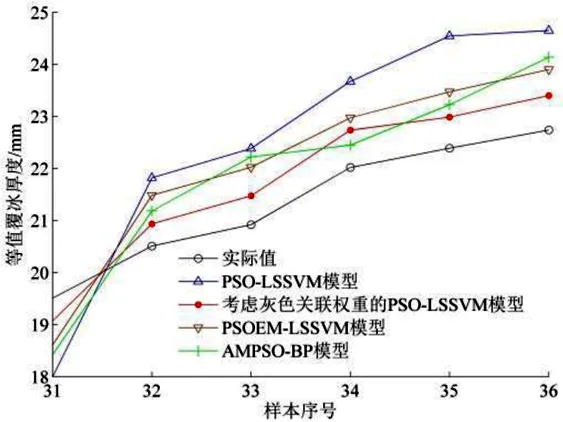
图3 测试数据预测值
表3给出了四种预测模型对测试集数据预测结果的各类误差。
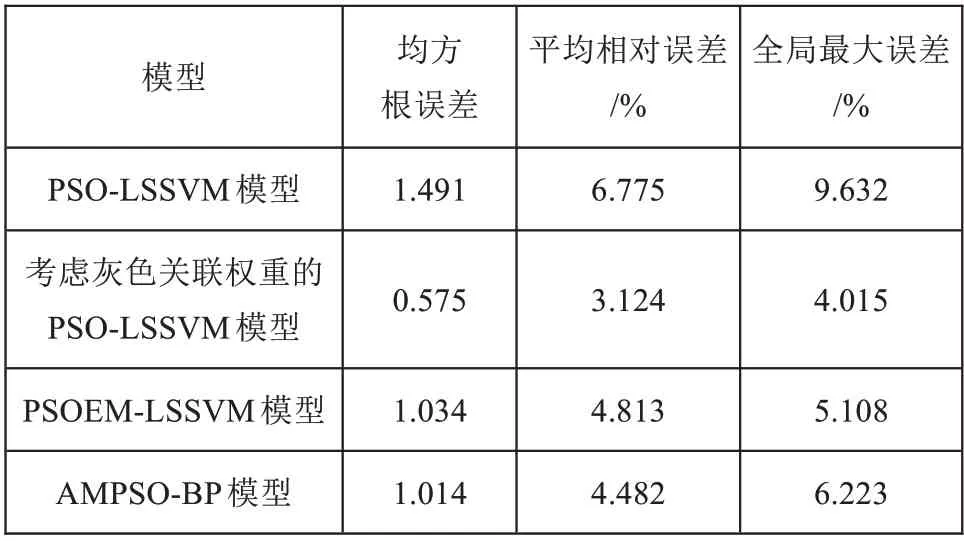
表3 四种模型预测误差对比
从表3可知,考虑灰色关联权重的PSO-LSSVM输电线路覆冰厚度预测模型对测试集预测的均方根误差、平均相对误差和全局最大误差分别为0.575、3.124%和4.015%,均小于其他三种预测模型,可见本文提出的考虑灰色关联权重的PSO-LSSVM 输电线路覆冰厚度预测模型能够降低数据外推过程中的数据波动,进一步提高覆冰厚度预测精度。
4 结论
(1)利用灰色关联分析确定覆冰影响因素对输电线路覆冰增长量的影响程度,计算出了各覆冰影响因素的灰色关联权重。采用PSO 算法对LSSVM的参数进行优化,建立了考虑灰色关联权重的PSOLSSVM输电线路覆冰厚度预测模型。
(2)采用实际运行线路的覆冰增长数据进行仿真分析,并与其他覆冰预测模型对比,结果表明,考虑灰色关联权重的PSO-LSSVM 输电线路覆冰厚度预测模型能够降低数据外推过程中的数据波动,进一步提高覆冰厚度预测精度。
