基于分布参数模型的高压输电线路双端测距算法研究
2022-03-05戴小剑钟建伟
戴小剑,田 波,李 愿,乔 华,周 璨,钟建伟
(1.国网湖北省电力有限公司恩施供电公司,湖北恩施 445000;2.湖北民族大学 信息工程学院,湖北恩施 445000)
引言
单端故障测距算法可利用的已知量太少,从而制约了单端测距算法的发展。随着信号传输技术的发展,采用双端故障测距算法可以克服单端测距算法的不足,结果较单端测距算法更为准确。
双端故障测距算法[1]按原理分类有两种,即两端数据同步和不同步的算法。两端数据同步的算法原理相对简单,但是需要设备来实现两端数据的同步,初始投入资金较高,测距结果的准确性主要取决于同步装置对数据同步的精确度,目前大多采用全球定位系统(GPS)的通信方式[2-4]。两端数据不需要同步的算法减少了硬件设备的资金投入,在实际中更有使用价值,这种算法较复杂,在伪根辨别问题上需要改进。
1 双端测距算法
1.1 两端数据需要同步的算法
双端电源系统的故障测距如图1 所示,过渡电阻为纯电阻性,对称且线路完全换位。在故障线路中,分别以r、g、L、C代表线路中单位长度的电阻、电导、电感、电容值。故障线路的波传播常数γ按式(1)计算,波阻抗Zc按式(2)计算。

利用P 端电气量代入均匀传输线方程,可以得到故障点电压为:

同理利用Q 端电气量,可以得到故障点电压为:

因为故障点电压不会突变,所以利用两侧电气量得到的故障点电压相等,即:
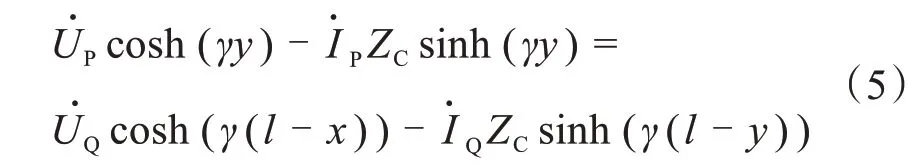
其中,
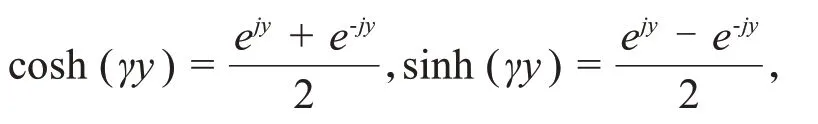
设γ=α+jβ表,式3.17可以化简为:
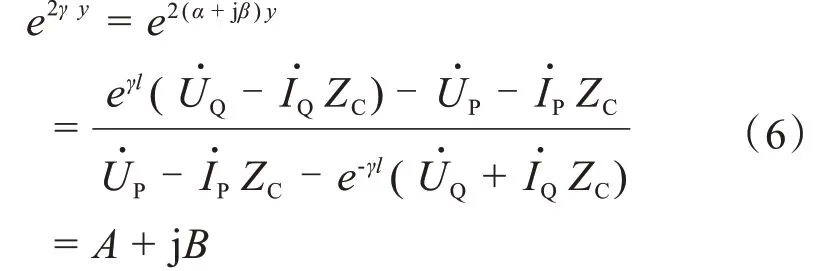
α为波传播常数γ的实部,α为实数,则:

=A2+B2
所以,可以计算得到故障距离为:
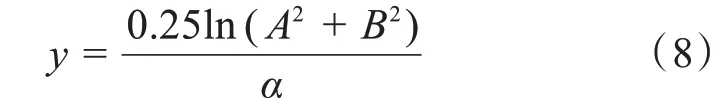
同理,可以得到由β表示的故障距离:
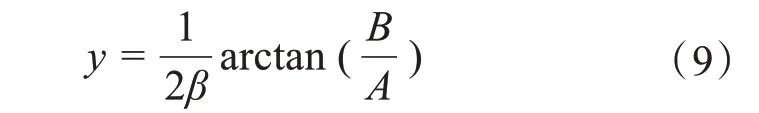
实际的高压输电线路上的电抗远远小于电阻,电容远远大于电导,所以波传播系数γ的实部远小于虚部,所以上面分别由α、β表示故障距离。
采用分布参数模型的两端数据需要同步的双端测距算法解决了过渡电阻和对端系统阻抗带来测距误差的问题,避免了输电线路分布电容带来测距的误差。
1.2 两端数据不需要同步的算法
采用有不同步角和故障距离两个未知量的方程求故障距离,可得故障距离为[5]:

采用两端电气量表示的故障点电压相量幅值相等求故障距离,可得故障距离为:
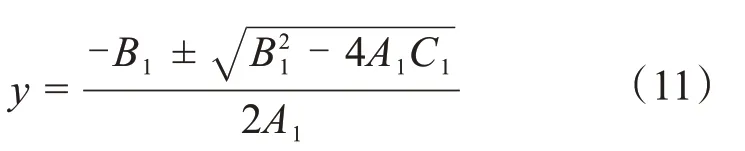
通过故障距离的公式可以清楚地知道它有两个解,一真一伪。若其中一个根小于零或者大于L,则这个根是伪根;若大于零且小于L,则这个根为真根,也就是所求的故障距离。
2 双端故障测距算法决定因素
双端故障测距算法优于单端故障测距算法。在实际中双端故障测距算法引入了通信通道,测距结果会产生误差。
(1)两端数据不同步
双端故障测距算法需要保证线路两侧电气量同步,如果存在不同步角差,无法实现准确测距,通信通道的引入就是为了解决这一问题。
基于通道的同步方法是在主从站间实现实时通信。但是在主从站间建立通信通道,技术要求较高,实现起来比较复杂,势必造成投入的资金也较大,费用高。利用故障前信息同步的方法比较简单,投资较小,但是适用范围有局限性,因为在有些情况下无法获得线路故障前的信息。基于GPS 的同步方法需依赖GPS来运行,同步误差不超过1 μs,但是设备造价高,这种同步方法目前应用比较广泛。
在工程实际中,电压互感器、电流互感器等对采集的数据会存在一定的延时,即同步技术也是没有办法做到数据完全同步的。因此,两端数据不需要同步的双端故障测距算法在实际运用中更为广泛。
(2)线路参数
在系统运行中,外界环境变化会导致输电线路的参数发生变化,同样,线路负荷的变化也会引起输电线路参数的变化。所以,如果在计算中采用固定的线路参数所得到的故障距离必定存在误差。
(3)线路不完全换位
在计算故障距离时,通常都将线路情况当做三相完全换位。在实际工程中,输电线路三相完全换位是从线路任意一端看进去的等效换位。当输电线路故障时,从故障点看,其两端的线路是不对称的。因此,在研究不同测距算法时对线路完全换位的假设,实际也对测距精度造成了一定影响。
(4)TA饱和
TA 饱和对故障测距的影响主要是使对端输送来的电流出现了形变,从而对依据测量端工频量的测距结果带来很大的偏差。特别是在大容积特高压的电力系统中,出现了金属性短路或者故障出现的地点再经过小阻抗短路,或者在电源、变电站的线路出口附近出现短路,十分容易产生TA 饱和现象。这种现象主要是因为铁芯的非线性特性造成电流互感器饱和。如果一个铁芯饱和,它的磁导率会快速下降,而励磁电流会急剧增大,大部分的一次电流会转变为励磁电流,将导致二次电流的严重缺损。
解决TA 饱和的办法主要有两种,一是补偿电流互感器中的饱和电流,二是在测距过程中只使用两端电压量或者两端电压和对端电流量,以避免TA饱和对测距结果的影响。
(5)故障暂态过程
在实际中,线路故障后会存在一个暂态过程,这会导致故障后的电压、电流中包含非周期分量、各次谐波分量,对测距结果带来误差。减小这一影响的主要方法是在故障测距前进行数字滤波。
3 算例仿真
为检验双端测距算法的测距精度及影响双端测距算法的因素造成的测距误差,分别以两侧电压电流法和两端数据不同步的算法进行了测距仿真[6-11]。
两侧电压电流算法解决了单端测距算法无法同时克服过渡电阻和对侧系统阻抗影响测距精度的问题,算法简单易懂,但需要保证两侧电气量同步。
利用MATLAB/Simulink 构建220 kV 高压输电线路模型,仿真模型如图2。对图2 设置参数后,可获得两侧电压电流法的测距结果。利用两端电气量表示的故障点电压相量幅值相等求故障距离的算法原理[12-15],两端数据不同步算法解决了两侧电气量不同步对测距结果带来的影响。

图2 220 kV输电线路故障仿真模型
4 仿真结果分析
4.1 带有过渡电阻短路
当线路A 相发生接地短路时,过渡电阻对测距精度的影响如表1~表3所示。由仿真结果可知,两端电压电流法不受过渡电阻的影响,在不同过渡电阻下,测距精度基本不变。该算法需要知道两侧数据,两侧系统阻抗均为已知量,故测距精度不受对侧系统阻抗影响。

表1 过渡电阻对双端测距算法的影响

表3 过渡电阻对双端测距算法的影响
4.2 不同步角差的影响
假设线路A 相经大小为50 Ω 的过渡电阻发生接地短路,不同步角差对测距精度的影响如表4~6所示。由仿真结果可知,不同步角差的存在,导致测距误差变得很大。因此,两侧电压电流法测距的准确性建立在两端数据同步的基础上,在两端数据不同步的情况下,这种算法无法准确测距。
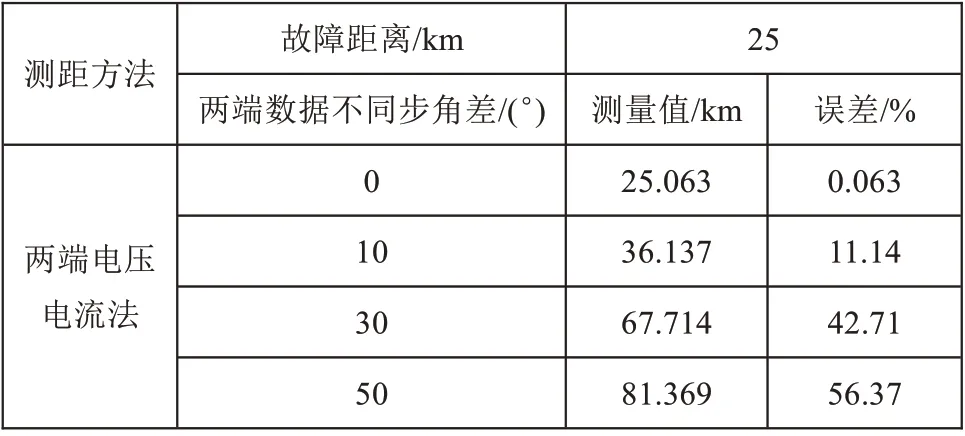
表4 不同步角差的影响
5 结论

表2 过渡电阻对双端测距算法的影响
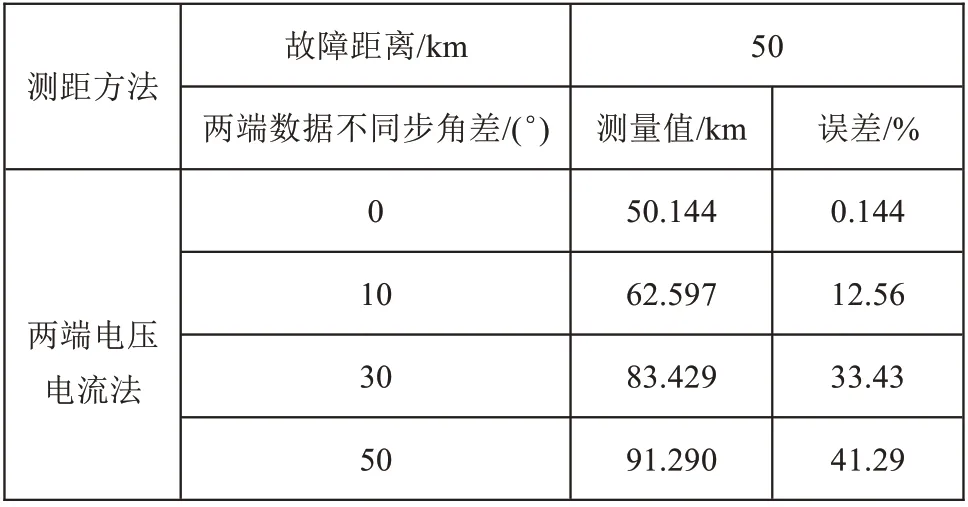
表5 不同步角差的影响
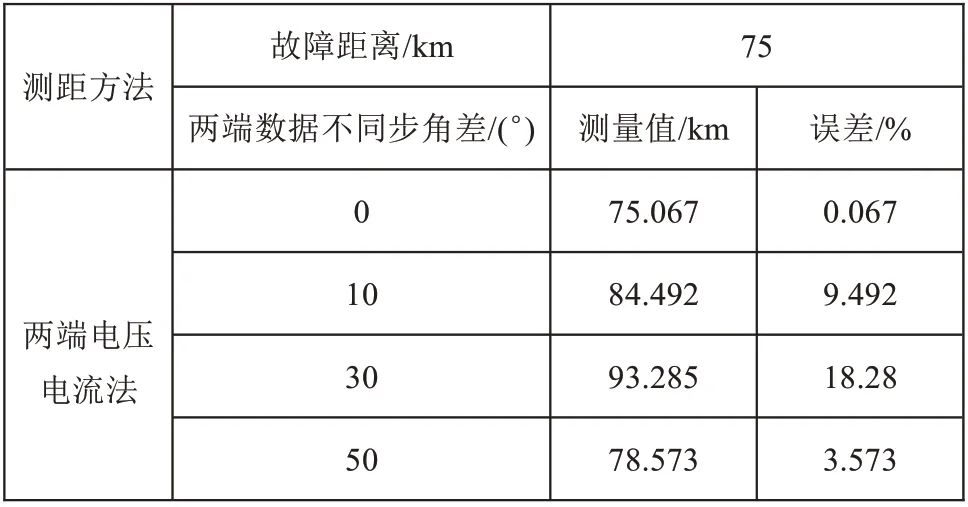
表6 不同步角差的影响
针对数据同步问题,详细介绍了两种不需要数据同步的双端测距算法的基本原理以及优缺点,主要包括采用含有不同步角和故障距离两个未知数的方程求故障距离的算法和利用两端电气量表示的故障点电压相量幅值相等求故障距离的算法。
在MATLAB/simulink 平台下,搭建高压输电线路仿真模型。仿真结果表明,两端数据同步算法的测距精度不受过渡电阻的影响,同时两侧系统阻抗为已知量,测距精度也不受对侧系统阻抗的影响,但受不同步角差的影响较大,在两端数据不同步的情况下,无法准确测距。在对各种双端测距算法分析的基础上,结合仿真结果,得出各个因素对双端测距算法的影响。本文提出的双端测距算法其测距结果更为精确,但其算法原理和计算量较单端测距算法复杂,并且需要建立通信通道保证两端数据的传递,增加了技术难度和投资,还有待于进一步的研究。
