基于量子元胞自动机的真随机数发生器设计

秦亚辰, 解光军

(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230601)

随着微纳电子器件技术的蓬勃发展,在后摩尔定律时代,寻找晶体管电路的理想替代者,一直是热门的研究问题。文献[1]提出了铝量子点元胞自动机模型,此后关于量子元胞自动机(quantum-dot cellular automata,QCA)电路的设计和研究成果层出不穷。基于择多逻辑[2-4]为基础逻辑的QCA电路可以实现类似于经典电路中的“与”“或”功能,辅以其独特的时钟循环机制[5]加以分割时序,亦可构建时序逻辑单元,时钟同时也为QCA电路提供能量,QCA时钟和传输线原理如图1所示。

图1 QCA时钟和传输线原理

随机数发生器(random number generator,RNG)模块在信息安全领域具有极其重要的应用价值,从经典的分组密码加密算法来看,不管是基于Feistel函数轮迭代的DES加密算法还是基于SP函数的AES算法,其密钥组成部分的选择尤为重要,要保证每轮通过移位置换操作生成的子密钥与明文进行异或运算后生成的密文不易被攻击者破解,对初始密钥的随机性具有较高的要求。相比较而言,序列密码加密算法更加倾向于逐位(bit)操作,其理论和技术已经十分成熟,且更容易硬件实现。

序列密码加密算法是简单的对合运算,属于对称密码的范畴,收发双方使用同一套密钥进行加密解密操作,加密解密过程即为简单的模二加运算,因此它对产生密钥的随机性具有很高的要求,可以说RNG每次产生密钥序列的随机性直接关系着加密的安全性。

在密码学领域,自同步序列密码加密解密过程常用的随机数发生器为线性反馈移位寄存器,linear feedback shift register,LFSR)[6],在GF(2n)有限域上选取适当的本原多项式作为反馈函数,产生的M序列最大周期T=2n-1,当T足够大时(远大于每次采样的密钥流的位数K),则可以认为生成的序列是随机的。

类似于LFSR的伪随机数发生器(pseudo-random number generator,PRNG)实现方案有很多种,PRNG生成的密钥流完全取决于“种子”序列和加密算法,理想的PRNG需要保证其算法的优异性能,使得生成序列在频率测试中保证“0”“1”出现的概率接近50%,同时要尽可能确保每次更换的“种子”序列随机。否则在长期的信道攻击下很可能被黑客掌握足够的数据,破解加密算法的规律。

相比较而言,真随机数发生器(ture random number generator,TRNG)则可以避免上述问题,达到香农提出的“一次一密”无条件安全的效果,自然界中有许多物理过程的演化规律是天然的随机源,如放射性衰变的脉冲周期和晶体管的热噪声等。

本文基于QCA元胞在传导极化过程中存在的不确定性因素作为随机源,设计TRNG电路,并对生成的序列进行随机性测试。

1 相关工作

1.1 QCA交叉耦合结构

交叉耦合结构[7-8]是QCATRNG设计的重要组成单元之一,如图2所示。文献[7]利用2个XNOR门和2个循环延迟结构设计1-bit的交叉耦合电路,该电路有一位的输入和输出,当输入CLK=0时,输出结果Qn=Qn-1,保持稳定状态;当CLK的状态从0→1时,由于QCA传输线环路信号的时钟延迟特性,导致接下来的每一个时钟周期Qn的值出现振荡,这种环路振荡的现象是将来每一位产生随机序列的根源。

图2 文献[7-8]提出的交叉耦合结构

只要将每一级输入不确定性的异步时钟信号CLKi作为“触发源”,在下一个时钟周期输出的Qi的值保持和反转的概率就各为50%,即可以实现生成真随机数的效果。文献[8]提出了基于交叉耦合结构的改进型电路。

所谓驱动下一级的不确定性异步时钟信号就需要交叉导向(cross-oriented)结构[7-8]来产生。

1.2 QCA交叉导向结构

新型的交叉耦合单元结构的原理图、版图及仿真结果如图3所示,交叉导向结构的2个输入端为A、B,其对中心元胞C的影响决定了输出端OUT被赋予的逻辑值。

根据静电累积原理[9]可以证明,当A⨁B=0时,C的状态稳定;当A⨁B=1时,输入端对中心元胞作用的总能量ET大致相等而抵消,因此元胞最终的输出状态不确定,即可以诱导中心元胞的亚稳态来作为驱动下一级交叉耦合结构的异步时钟,这是QCA元胞自带的物理属性。文献[7-8]以及本文提出的交叉导向结构的性能对比见表1所列。

表1 几种交叉耦合结构的性能参数对比

2 新型的TRNG电路设计

2.1 新型单元结构的设计与分析

基于1.1节对1-bit交叉耦合结构的分析可以得出:当CLK=0时,电路的输出OUT处于锁存状态;当CLK=1时,在高电平脉冲到来的下一个时钟周期,信号被反转,此后一直振荡,直到低电平信号到来的下一个时钟周期截止。根据此原理,可以直接利用现有的QCA2-input异或门[10]结构,辅以合适的延迟线路,实现交叉耦合结构原有的输出逻辑关系,即

Ot+1=CLK⊕Ot

(1)

其中:Ot+1为t+1时的OUT;CLK为CLK;Ot为t时的OUT。

2.2 TRNG电路的原理

在完成对交叉耦合结构的设计之后,再利用1.2节中提到的交叉导向结构便可以实现位拓展的功能,构建n-bit(n=2k,k∈Z+)TRNG电路,QCA双8-bit TRNG电路如图4所示。这里n为偶数,是为了使设计的电路更加对称工整。该TRNG电路在一个时钟周期循环内可以一次性产生2组不同的k-bit真随机数密钥,这2组密钥之间相互独立存在。电路唯一的输入即为CLK,当设备工作时,CLK可以人为设置一组0/1序列作为“种子”输入。

图4 QCA双8-bit TRNG电路

不同于PRNG电路,此时CLK作为种子输入的作用被弱化到仅仅具有开关的意义,每次启动设备时,由于QCA循环延迟电路自身的物理属性,赋予初始值的“抽头序列”会随着元胞传递极化值而瞬态响应,最终建立起稳定的状态被随机分配为“0”“1”的输出,与图2所示的2种结构相比较,新型的交叉耦合结构电路被简化了。延迟、功耗、所消耗的元胞数目和电路面积都进一步减小。显然,利用新的单元结构的位拓展设计n-bit TRNG电路将获得更加优化的量子成本。因此该TRNG电路每次启动的初始值是一个k-bit的真随机数,再加上交叉导向结构对每一级电路异步时钟信号(CLKi)的随机性诱导,便可以保证每一级输出“0”“1”的概率相等。

QCA双8-bit TRNG随机一次测试的仿真结果如图5所示。

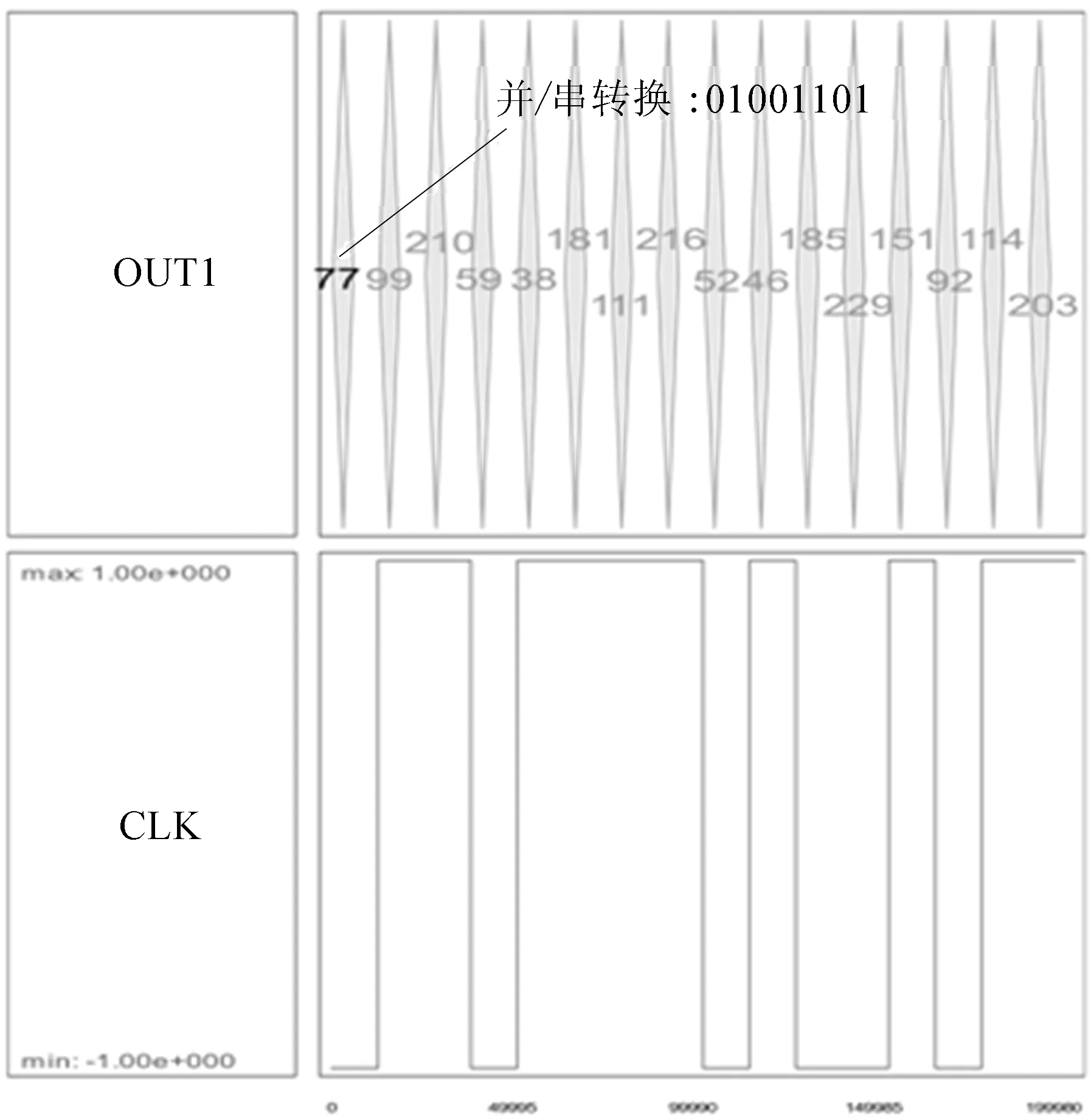
图5 QCA双8-bitTRNG随机一次测试的仿真结果

设存在一个2k-bit(k∈Z+)的该类TRNG电路,在设定输出随机序列的选择方法上,首先假设OUT[O1,O2,O3,…,O2k-1,O2k]为目标的随机序列,其中OUT可以表示为GF(22k)有限域上的一个特征多项式。

由交叉导向结构提供的异步时钟信号CLKi(0≤i≤k),输出值为0或1的概率各为50%,尽管如此,驱动第i级交叉耦合结构的输出值却只有保持或者反转2种方式,即

00→00/11,01→01/10,10→10/01,11→00/11。

假设在任意时刻采样到了一组OUT的值,其中00、01、10、11的个数分别为a、b、c、d。根据马尔可夫矩阵可以推导出以下关系:

(2)

经过p(p≥1)次轮迭代之后,输出序列OUTp中2个连续位上00、01、10、11共4种状态分别对应的个数即为等式右边行向量的每个元素。此时OUTp取值的可能性共有:

(3)

设a+d=m,b+c=k-m。根据Γ函数对(3)式分母进行展开,则有:

(4)

根据上述推导过程可以得知,按照文献[7-8]中的输出设置,OUT[O1,O2,O3,…,O2k-1,O2k]一次理论上最大只能产生2k种可能的真随机数,其电路使用的量子成本并非最优化,因为存在2k个输出位,相当于每次设备开始工作时,所以其随机的初始状态OUT决定了输出在一个固定的循环中演化,而这样的初始状态也存在2k种。

对现有的TRNG电路输出设置进行改进,取OUT1[O1,O3, …,O2k-1]和OUT2[O2,O4, …,O2k]2组相互独立的k-bit输出序列作为最终的输出值,通过分析可以得出,2组序列中任意一位每次在异步时钟信号的诱导下,输出0/1的概率皆为5%,服从概率空间I上严格的均匀分布。且2组序列对应的初始状态皆随机且相互独立。现引入自信息量[11]和无条件熵[12]的概念,即

I(xi)=-lbp(xi)

(5)

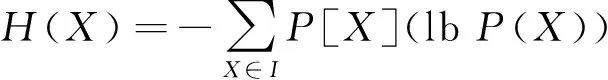
(6)

其中,xi为概率空间上任一元素。自信息量在密钥序列发出之前可以表示信源的不确定度。

(7)

当且仅当Pi=1/n时H(X)取极大值。本文提出的输出位改进模型对应如下运算关系:

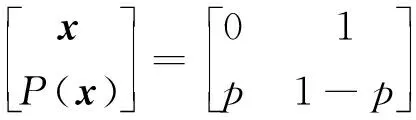
(8)

(9)

当且仅当p=1-p时,无条件熵取极大值1。此时p=0.5。因此在QCATRNG电路中,按照上述方法输出OUT的值,理论上可以使系统输出获得最大的不确定度。

3 电路性能的测试与仿真

n-bit(n=2k,k∈Z+)TRNG电路一个时钟周期内能够产生2组相互独立的k-bit的随机序列,在实际应用的过程中结合QCA并/串结构[13]或是移位寄存器组来实现密钥流的输出,因为现有的工艺水平以及仿真软件功能的限制,所以只能对生成的结果进行局部的随机性测试。测试对象为双8-bit TRNG电路(图4),设置16个时钟周期循环,取其中任意一组输出矢量OUT1,经过并/串转换之后生成16 byte的密钥流(图5)。

根据上述仿真结果,取OUT1作为被测数据,测试手段为美国国家标准技术研究院(National Institute of Standards and Technology,NIST)提供的几种指标[14]。

NIST随机性测试标准见表2所列。

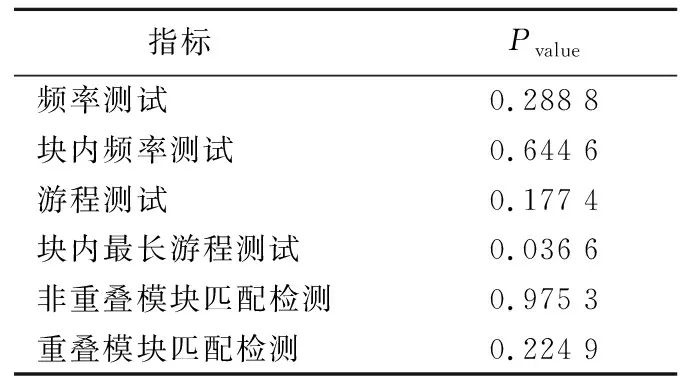
表2 NIST随机性测试标准

经过局部的随机性测试,产生的16 byte密钥流对应的测量参数Pvalue≥0.01,证明生成的序列具有随机性。测试过程中涉及到的重要函数为误差函数(erfc)、非完全伽马函数(igamc),其数据处理和计算结果由matlab函数库提供支持。

4 结 论

本文结合QCA自身的物理性质,对原有的交叉耦合结构进行了深入的分析,利用其输出特性,在原有的基础上进行了逻辑综合优化[15],设计了一种新型的QCA TRNG单元结构,该结构具有元胞面积小、低延迟的特性,且便于进行位拓展的操作。双8-bit TRNG电路基于简化的单元结构和交叉导向结构共同实现。对输出位的设置相比较之前的工作来看,通过数学推导证明了选取奇数位和偶数位独立输出可以使系统获得最大的不确定度。

目前相关的工作仍然存在一些问题尚待解决。QCATRNG电路是采用并行输出方式的,即一个时钟周期产生k-bit的输出序列,这就需要利用并串技术把生成的一组输出矢量转化为密钥流同明文进行逐位加密,这一过程必然会增加通信电路整体的时序冗余,但是并行的输出结果如果应用于分组密码加密系统,那么可以省去轮密钥生成算法中置换、移位等线性操作,相当于每一轮的加密都使用了独立的密钥,这就让分组密码机制中除了S-box之外,又增加了另一个非线性因素,对加密的安全性有着本质的提升,而且在每一轮加密的过程中,RNG的电路结构和输入的“种子”(即CLK)都不需要做任何的变化,这在经典电路中是难以想象的,如达到同样的效果必须要耗费巨大的硬件成本。另外,真随机数也存在天然的缺陷,因为伪随机数是由特定算法生成的,所以其0/1分布相对均匀,对应的块内频率测试的值更加合理,而真随机数的本质是因为物理过程的演变而量化的结果,所以其存在0/1集中分布的概率是很大的,如果直接应用于加密操作,很可能会导致部分子块内的密文信息泄露,那么后续的工作会考虑到在并行输出的后端再加上一级具有混淆功能的P-box,至于变换矩阵的算法,设想依照QCA物理模型对应的“熵源”交叉耦合结构和交叉导向结构内在的演化规律同温度、元胞距离等参数的关系,再根据本文设计的TRNG输出结果进行大量的数据测试和统计,最终利用QCA的可逆逻辑门[16-17]电路,实现对P-box的最优化的设计。